On Skew Triangular Matrix Rings
Wang Wei-liang,Wang Yaoand Ren Yan-li
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin,300072)
(2.School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing,210044)
(3.School of Information Engineering,Nanjing Xiaozhuang University,Nanjing,211171)
Communicated by Du Xian-kun
On Skew Triangular Matrix Rings
Wang Wei-liang1,Wang Yao2,*and Ren Yan-li3
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin,300072)
(2.School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing,210044)
(3.School of Information Engineering,Nanjing Xiaozhuang University,Nanjing,211171)
Communicated by Du Xian-kun
Let α be a nonzero endomorphism of a ring R,n be a positive integer and Tn(R,α)be the skew triangular matrix ring.We show that some properties related to nilpotent elements ofRare inherited by Tn(R,α).Meanwhile,we determine the strongly prime radical,generalized prime radical and Behrens radical of the ring R[x;α]/(xn),where R[x;α]is the skew polynomial ring.
skew triangular matrix ring,skew polynomial ring,weak zip property,strongly prime radical,generalized prime radical
2010 MR subject classification:16N20,16S36
Document code:A
Article ID:1674-5647(2016)03-0259-13
1 Introduction
Throughout this paper,R denotes an associative ring with identity and α is a nonzero endomorphism of R.For a given ring R,we use nil(R),Nil∗(R),Nil∗(R),L-rad(R)and J(R)to denote the set of all nilpotent elements,the prime radical,the upper nilradical,the Levitzki radical and the Jacobson radical of R,respectively.We denote by R[x;α]the skew polynomial ring,whose elements are the polynomials over R,the addition is defined as usual,and the multiplication subject to the relation xr=α(r)x for any r∈R.For a positive integer n,the skew triangular matrix ring is defined as
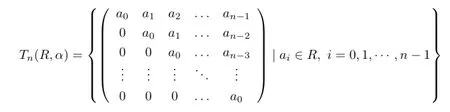
with addition pointwise and multiplication given by
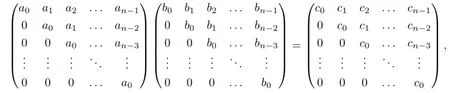
where

We denote elements of Tn(R,α)by(a0,a1,···,an−1).It is easy to verify that the σ:Tn(R,α)-→R[x;α]/(xn)defined by σ(a0,a1,···,an−1)=a0+a1x+···+an−1x+(xn) is a ring isomorphism,where ai∈R,0≤i≤n-1,(xn)is the ideal generated by xn.
The triangular matrix ring Tn(R)and the quotient R[x]/(xn)of a polynomial ring R[x] has attracted a lot of attention(see[1]–[3]).Nasr-Isfahani and Moussavi[4]discussed their right mininjective,right T-nilpotent and right Kasch property.In recent,Nasr-Isfahani[5]extended the study to the skew triangular matrix ring Tn(R,α)and gave their prime,primitive and maximal ideals.We continue in this paper investigate some properties of Tn(R,α) and determine the strongly prime radical,generalized prime radical and Behrens radicals of the quotient ring R[x;α]/(xn).
2 Properties Related to Nilpotent Elements
Recall that a ring R is reduced if R has no nonzero nilpotent elements,R is an NI ring if nil(R)=Nil∗(R),R is 2-primal if nil(R)=Nil∗(R),R is weakly 2-primal if nil(R)=L-rad(R),and R is locally 2-primal if each finite subset generates a 2-primal ring.A ring R is called nil-semicommutative if for every a,b∈R,ab∈nil(R)implies aRb⊆nil(R),and R is called weakly semicommutative if for any a,b∈R,ab=0 implies aRb⊆nil(R).The following implications hold:
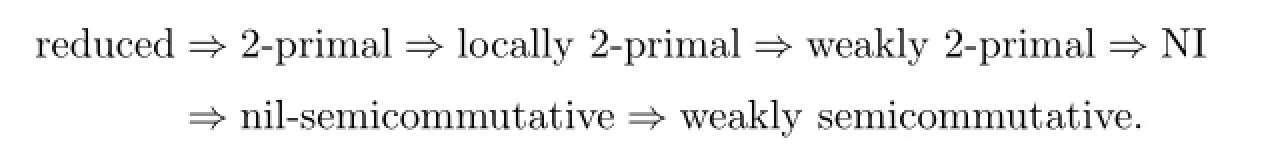
In general,each of these implications is irreversible(see[6]).
Observe that nil(Tn(R,α))=(nil(R),R,···,R),we have that a ring R is reduced if and only if
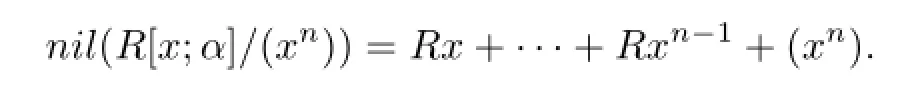
Proposition 2.1(1)Tn(R,α)is locally 2-primal if and only if R is locally 2-primal;
(2)Tn(R,α)is weakly 2-primal if and only if R is weakly 2-primal;
(3)Tn(R,α)is an NI ring if and only if R is an NI ring.
Proof.(1)Suppose that R is locally 2-primal and M⊆Tn(R,α)is a finite subset,say M=(M0,M1,···,Mn−1).Thenis 2-primal and nilwheredenotes the subring of R generated by S.Notice thatandby Theorem 2.8 of[5],we obtain thatSo Tn(R,α)is locally 2-primal.
Conversely,assume that Tn(R,α)is locally 2-primal.Then for any finite subset M⊆R,⟩is 2-primal.Sinceand Nil∗,we have thatSo R is locally 2-primal.
(2)Suppose that R is weakly 2-primal.Then nil(R)=L-rad(R).By Theorem 2.19 of [5],we have
L-rad(Tn(R,α))=(L-rad(R),R,···,R)=(nil(R),R,···,R)=nil(Tn(R,α)). It shows that Tn(R,α))is weakly 2-primal.
Conversely,assume that Tn(R,α)is weakly 2-primal.Then from argument above it is easy to see that L-rad(R)=nil(R).
(3)Suppose that R is an NI ring.Then nil(R)=Nil∗(R).By Theorem 2.14 of[5],we have
Nil∗(Tn(R,α))=(Nil∗(R),R,···,R)=(nil(R),R,···,R)=nil(Tn(R,α)). Hence Tn(R,α))is an NI ring.
Conversely,assume that Tn(R,α)is an NI ring.Then from
Nil∗(Tn(R,α))=(Nil∗(R),R,···,R)=(nil(R),R,···,R)=nil(Tn(R,α)),we have nil(R)=Nil∗(R).
Corollary 2.1(1)R[x;α]/(xn)is locally 2-primal if and only if R is locally 2-primal;
(2)R[x;α]/(xn)is weakly 2-primal if and only if R is weakly 2-primal;
(3)R[x;α]/(xn)is an NI ring if and only if R is an NI ring.
Proposition 2.2(1)Tn(R,α))is weakly semicommutative if and only if R is weakly semicommutative;
(2)Tn(R,α))is nil-semicommutative if and only if R is nil-semicommutative.
Proof.(1)Suppose that R is weakly semicommutative and(a0,a1,···,an−1)(b0,b1,···,bn−1)=0.Then a0b0=0 gives a0Rb0⊆nil(R).It follows that(a0,a1,···,an−1)(c0,c1,···,cn−1)(b0,b1,···,bn−1)∈nil(Tn(R,α))for any(c0,c1,···,cn−1)∈Tn(R,α).
Conversely,assume that Tn(R,α)is weakly semicommutative.Then for any a,b∈R with ab=0,(a,0,···,0)(b,0,···,0)=0 implies that(a,0,···,0)Tn(R,α)(b,0,···,0)⊆nil(Tn(R,α))=(nil(R),R,···,R).It follows that aRb⊆nil(R).
(2)Suppose that R is nil-semicommutative and(a0,a1,···,an−1)(b0,b1,···,bn−1)∈nil(Tn(R,α)).Then a0b0∈nil(R)implies a0Rb0⊆nil(R).It follows that
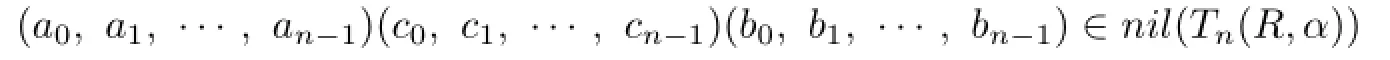
for any(c0,c1,···,cn−1)∈Tn(R,α).
Conversely,assume that Tn(R,α)is nil-semicommutative.Then for any a,b∈R with ab∈nil(R),we get(a,0,···,0)(b,0,···,0)∈nil(Tn(R,α)).Since Tn(R,α)is nilsemicommutative,(a,0,···,0)Tn(R,α)(b,0,···,0)⊆nil(Tn(R,α)).It implies that aRb∈nil(R).
Corollary 2.2(1)R[x;α]/(xn)is weakly semicommutative if and only if R is weakly semicommutative;
(2)R[x;α]/(xn)is nil-semicommutative if and only if R is nil-semicommutative.
Lemma 2.1If R is weakly 2-primal and f(x)=a0+a1x+···+anxn∈R[x],then f(x)∈nil(R[x])if and only if ai∈nil(R)for each 0≤i≤n,that is,we have nil(R[x])= nil(R)[x].
Proof.Let f(x)=a0+a1x+···+anxn∈nil(R[x]).Then there exists some positive integer k such that 0=f(x)k=(a0+a1x+···+anxn)k=“lower terms”+.Using induction on n,we obtain ai∈nil(R)for each 0≤i≤n.So nil(R[x])⊆nil(R)[x].
Now assume that

Consider the finite subset{a0,a1,···,an}.Since nil(R)=L-rad(R),the subringof R generated by{a0,a1,···,an}is nilpotent.Thus,there exists a positive integer k such that any product of k elements ai1ai2···aikfrom{a0,a1,···,an} is zero.So f(x)k+1=0 and f(x)∈nil(R[x]).This shows that nil(R[x])=nil(R)[x].The proof is completed.
A ring R is called weak symmetric if for a,b,c∈R,abc∈nil(R)implies acb∈nil(R).
Proposition 2.3Let R be a weakly 2-primal ring.Then the following statements are equivalent:
(1)R is weak symmetric;
(2)R[x]is weak symmetric;
(3)Tn(R,α)is weak symmetric;
(4)R[x;α]/(xn)is weak symmetric.
Proof.(1)⇒(2).Since any subring of a weak symmetric ring is also weak symmetric.
(2)⇒(1).Suppose that R is weak symmetric.Let f(x)=a0+a1x+···+anxn,g(x)=b0+b1x+···+bmxmand h(x)=c0+c1x+···+clxl∈R[x]with fgh∈nil(R[x]). Then we have the following equations by Lemma 2.1:
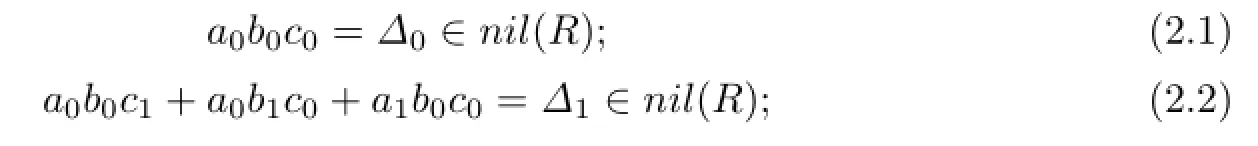
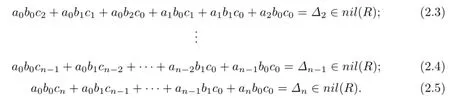
Since nil(R)is an ideal of R,(2.1)implies that c0a0b0∈nil(R),and hence b0c0a0∈nil(R). If we multiply(2.2)on the left hand side by b0c0,then we have

This implies that b0c0a1b0c0∈nil(R)and a1b0c0∈nil(R).So we have
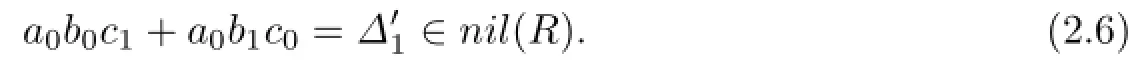
If we multiply(2.6)on the right hand side by a0b0,then we have a0b1c0a0b0∈nil(R),a0b0c1a0b0∈nil(R),and hence a0b0c1∈nil(R),a0b1c0∈nil(R).
If we multiply(2.3)on the right hand side by a0b0,a0b1,a0b2,and a1b0,respectively,then we obtain a0b0c2,a0b1c1,a0b2c0,a2b0c0,a1b0c1,a1b1c0∈nil(R)in turn.
Inductively we assume that aibjck∈nil(R)for i+j+k≤n-1.We apply the above method to(2.5).If we multiply(2.5)on the left hand side by b0c0,then we have anb0c0∈nil(R)by the induction hypotheses,and
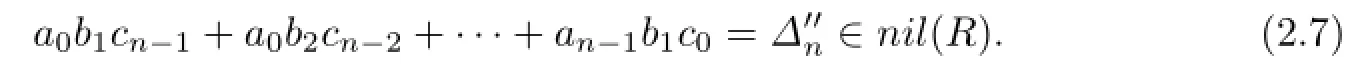
If we multiply(2.7)on the right hand side by a0b1,it gives a0b1cn−1∈nil(R),and

If we multiply(2.8)on the right hand side by a0b2,a0b3,···,an−1b1,respectively,then we obtain a0b2cn−2∈nil(R),a0b3cn−3∈nil(R),···,an−1b1c0∈nil(R)in turn.By induction,this shows that aibjck=0 for all i,j and k with i+j+k=n.Since R is weak symmetric,aickbj∈nil(R)for all i,j,k with i+j+k≤n.Since the coefficients of fhg can be written as sums∑aickbj,we have coef(fhg)⊆nil(R).This yields fhg∈nil(R)[x]= nil(R[x])by Lemma 2.1.
(1)⇔(3).Suppose that Tn(R,α)is weak symmetric and A=(aij),B=(bij),C= (cij)∈Tn(R,α)with ABC∈nil(Tn(R,α)),where aij=0,bij=0,cij=0 for all i>j.Then aiibiicii∈nil(R)implies aiiciibii∈nil(R)for all 0≤i≤n.This yields ACB∈nil(Tn(R,α)).Conversely,assume that Tn(R,α)is weak symmetric.For a,b,c∈R with abc∈nil(R),aIbIcI∈nil(Tn(R,α))implies that aIcIbI∈nil(Tn(R,α)),where I is the n×n identity matrix.This gives that acb∈nil(R).The proof is completed.
We call a ring R is an NJ-ring if nil(R)=J(R).Nil rings and Artinian NI rings are NJ-rings,and NJ-rings are NI rings.
Example 2.1(1)Let G be an abelian group and not torsion,and R be a commutative ring.Then J(RG)=nil(RG)by Corollary 43.8 of[7].So RG is an NJ-ring.
(2)Let A,B be rings andAVBan(A,B)-bimodule.Thenis an NJ-ring if and only if A,B are both NJ-rings.
Proposition 2.4The following statements are equivalent for a ring R:
(1)R is an NJ-ring;
(2)R is NI and R/Nil∗(R)is J-semisimple.
Proof.(1)⇒(2).Since nil(R)=J(R)is an ideal of R,Nil∗(R)=nil(R)=J(R).Hence R is an NI ring and R/Nil∗(R)is J-semisimple.
(2)⇒(1).Nil∗(R)=nil(R)⊆J(R).Since J(R/Nil∗(R))=0,J(R)⊆Nil∗(R)⊆nil(R).
Proposition 2.5(1)Tn(R,α)is an NJ-ring if and only if R is an NJ-ring;
(2)R[x;α]/(xn)is an NJ-ring if and only if R is an NJ-ring.
Proof.Suppose nil(R)=J(R).By Corollary 3.2 of[5],we have
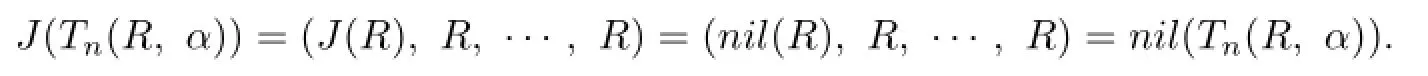
Conversely,assume that Tn(R,α)is an NJ-ring.Then from J(Tn(R,α))=(J(R),R,···,R) and nil(Tn(R,α))=(nil(R),R,···,R)we have
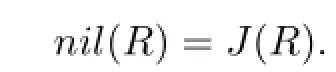
The proof is completed.
By[8],a ring R is called Brown-McCoy ring if every prime ideal of R is an intersection of maximal ideals.As a corollary of Theorem 2.8,Corollary 2.9,Theorem 3.9 and Corollary 3.10 in[5],we have the following
Proposition 2.6(1)Tn(R,α)is a Brown-McCoy ring if and only if R is a Brown-McCoy ring;
(2)R[x;α]/(xn)is a Brown-McCoy ring if and only if R is a Brown-McCoy ring.
Recall that a ring R is called weak Armendariz if whenever two polynomials f(x),g(x)∈R[x]satisfy f(x)g(x)=0,then ab∈nil(R)for all a∈coef(f(x))and b∈coef(g(x));and R is called nil Armendariz if whenever two polynomials f(x),g(x)∈R[x]satisfy f(x)g(x)∈nil(R)[x],then ab∈nil(R)for all a∈coef(f(x))and b∈coef(g(x)),where coef(f(x)) denotes the subset of R of the coefficients of f(x).Notice that Armendariz rings are both weak Armendariz and nil Armendariz,and nil Armendariz rings are weak Armendariz(see [9]).
Proposition 2.7(1)Tn(R,α)is weak Armendariz if and only if R is weak Armendariz;
(2)Tn(R,α)is nil Armendariz if and only if R is nil Armendariz. Proof.(1)Suppose that R is weak Armendariz andTn(R,α)[x]with f(x)g(x)=0.Putting Ai=(ai0,ai1,···,ain−1)for 0≤i≤n and Bj=(bj0,bj1,···,bjn−1)for 0≤j≤m,we have

and

Since R is weak Armendariz,ai0bj0∈nil(R)for any i,j.This implies AiBj∈nil(Tn(R,α)). So Tn(R,α)is weak Armendariz.Conversely,since the subrings of a weak Armendariz ring are weak Armendariz,we know that R is weak Armendariz.
(2)It is similar to the proof of(1).
Corollary 2.3(1)R[x;α]/(xn)is weak Armendariz if and only if R is weak Armendariz;
(2)R[x;α]/(xn)is nil Armendariz if and only if R is nil Armendariz.
For a subset X of a ring R,
NR(X)={a∈R|xa∈nil(R)for all x∈X}={b∈R|bx∈nil(R)for all x∈X} is called the nilpotent annihilator of X in R.A ring R is called nilpotent p.p.-ring(resp.,nilpotent Baer ring)if for any element p∈R(resp.,subset X⊆R)with NR(p)̸=R(resp.,NR(X)̸=R)is generated as a right ideal by a nilpotent element,and R is called weak zip provided that NR(X)⊆nil(R),where X is a subset of R,then there exists a finite subset Y⊆X such that NR(Y)⊆nil(R)(see[10]).
Proposition 2.8Let R be a domain and α an epimorphism of R.Then we have
(1)Tn(R,α)is a nilpotent p.p.-ring;
(2)Tn(R,α)is a nilpotent Baer ring.
Proof.(1)Suppose that p=(a0,a1,···,an−1)∈Tn(R,α)with NTn(R,α)(p)̸=Tn(R,α). Note that NTn(R,α)(p)=(NR(p),R,···,R).If a0=0,which implies NTn(R,α)(p)= Tn(R,α),a contradiction.Thusand NTn(R,α)(p)={(0,b1,···,bn−1)|b1,···,bn−1∈ R}since R is a domain.For any(0,b1,···,bn−1)∈NTn(R,α)(p),since α is a epimorphism,there exists an a0∈R such that α(a0)=b1,a1∈R such that α(a1)=b2-α2(a0),···,and an−2∈R such that α(an−2)=bn−1-αn−1(a0)-···-α2(an−3).This shows that (0,b1,···,bn−1)=(0,1,1,···,1)(a0,a1,···,an−2,0).So we have NTn(R,α)(p)= (0,1,1,···,1)Tn(R,α),where(0,1,1,···,1)is a nilpotent element of Tn(R,α).Therefore,Tn(R,α)is a nilpotent p.p.-ring.
(2)It is similar to the proof of(1).
Corollary 2.4(1)R[x,α]/(xn)is a nilpotent p.p.-ring;
(2)R[x,α]/(xn)is a nilpotent Baer ring.
Proposition 2.9(1)Tn(R,α)is weak zip if and only if R is weak zip;
(2)R[x,α]/(xn)is weak zip if and only if R is weak zip.
Proof.Suppose that R is weak zip and X⊆Tn(R,α)with NTn(R,α)(X)⊆nil(Tn(R,α)). Let X0={b0∈R|(b0,b1,···,bn−1)∈X}.For any a0∈NR(X0),we have b0a0∈nil(R) and(a0,0,···,0)∈NTn(R,α)(X)⊆nil(Tn(R,α))=(nil(R),R,···,R).It follows a0∈nil(R),and hence NR(X0)⊆nil(R).Since R is weak zip,there exists a finite subset Y0⊆X0such that NR(Y0)⊆nil(R).For each b∈Y0,we take onePut Y={Ab|b∈Y0}.Then Y is a finite subset of X.We have
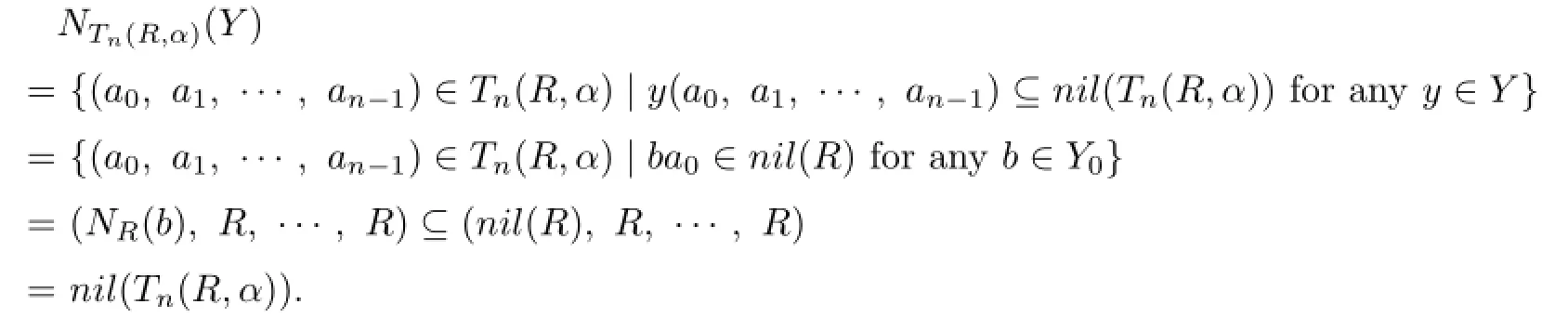
So Tn(R,α)is weak zip.
Conversely,assume that Tn(R,α)is weak zip and X⊆R with NR(X)⊆nil(R).Let Y= {xI|x∈X}⊆Tn(R,α),where I is the n×n identity matrix.If A=(a0,a1,···,an−1)∈NTn(R,α)(Y),then xI·A∈nil(Tn(R,α))for all x∈X.This implies that xa0∈nil(R)and a0∈NR(X))⊆nil(R).Thus,we have A=(a0,a1,···,an−1)∈nil(Tn(R,α))and hence NTn(R,α)(Y)⊆nil(Tn(R,α)).So there exists a finite subset Y0={x1I,x2I,···,xmI}⊆Y such that NTn(R,α)(Y0)⊆nil(Tn(R,α)).Let X0={x1,x2,···,xm}⊆X.Then
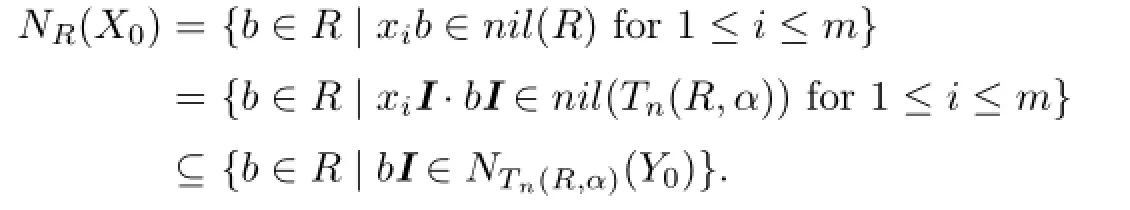
Since NTn(R,α)(Y0)⊆(nil(R),R,···,R),NR(X0)⊆nil(R).Therefore,R is weak zip.
3 Radical Properties
Recall that an ideal P of a ring R is completely prime if ab∈P implies that a∈P or b∈P for a,b⊆R,and the generalized nil radical Ng(R)of R is the intersection of all the completely prime ideal of R.The following proposition is a direct corollary of Theorem 2.10 and Corollary 2.11 in[5].
Proposition 3.1For any ring R and n≥1,
(1)Ng(Tn(R,α))=(Ng(R),R,···,R);
(2)Ng(R[x;α]/(xn))=Ng(R)+Rx+···+Rxn−1+(xn).
A ring R is called right strongly prime if for any non-zero element a∈R,there is a right insulator,that is,a finite set Fa⊆R such that for all z∈R,aFaz=0 implies z=0.A ring is called uniformly strongly prime if the same insulator may be chosen for each nonzero element(see[11]).It is clear that every right strongly prime ring(resp.,uniformly strongly prime ring)is prime.An ideal I of R is said to be a right strongly prime ideal of R if the ring R/I is a right strongly prime ring,equivalently,an ideal I of R is right strongly prime if and only if for every x/∈I,there is a finite subset F of(x)such that for all z∈R,Fz⊆I implies z∈I.An ideal I of a ring R is called uniformly strongly prime ideal of R if R/I is a uniformly strongly prime ring.The intersection sr(R)of all the right strongly prime ideal of R is called the right strongly prime radical of R.The uniformly strongly prime radical ofa ring R,denoted by us(R),is the intersection of all the uniformly strongly prime ideal of R.
Proposition 3.2Let α be a nonzero endomorphism of R with α(1)=1.Then we have
(1)An ideal Q of the ring Tn(R,α)is strongly prime if and only if Q=(P,R,···,R) for some strongly prime ideal P of R;
(2)An ideal Q of the ring R[x;α]/(xn)is strongly prime if and only if Q=P+Rx+ ···+Rxn−1+(xn)for some strongly prime ideal P of R;
(3)An ideal Q of the ring Tn(R,α)is uniformly strongly prime if and only if Q= P+Rx+···+Rxn−1+(xn)for some uniformly strongly prime ideal P of R;
(4)An ideal Q of the ring R[x;α]/(xn)is uniformly strongly prime if and only if Q= P+Rx+···+Rxn−1+(xn)for some uniformly strongly prime ideal P of R.
Proof.(1)Suppose that Q is a strongly prime ideal of Tn(R,α).For any(a0,a1,···,an−1)∈Tn(R,α),by α(1)=1,we have
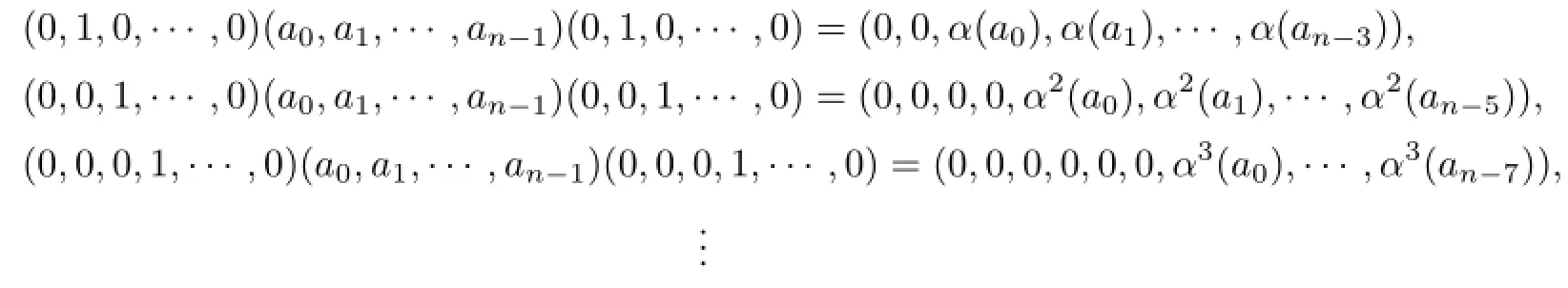
If n=2k,

if n=2k+1,
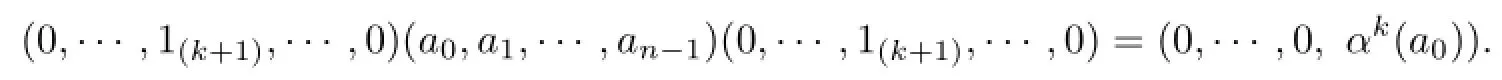
Since Q is a prime ideal,by(0,0,···,1)Tn(R,α)(0,0,···,1)=0⊆Q,we have(0,0,···,1)∈Q,and by(0,0,···,1,0)Tn(R,α)(0,0,···,1,0)=0⊆Q,we have(0,0,···,1,0)∈Q.
Repeating this step to step n-k.
If n=2k,we get(0,···,1(k+1),···,0)Tn(R,α)(0,···,1(k+1),···,0)=0⊆Q,and hence (0,···,1(k+1),···,0)∈Q.
If n=2k+1,we get(0,···,1(k+1),···,0)Tn(R,α)(0,···,1(k+1),···,0)⊆(0,···,0,R)⊆Q,and hence(0,···,1(k+1),···,0)∈Q.
Since(0,···,1(k+1),···,0)∈Q,(0,0,···,1,0)∈Q and(0,0,···,1)∈Q,we now have
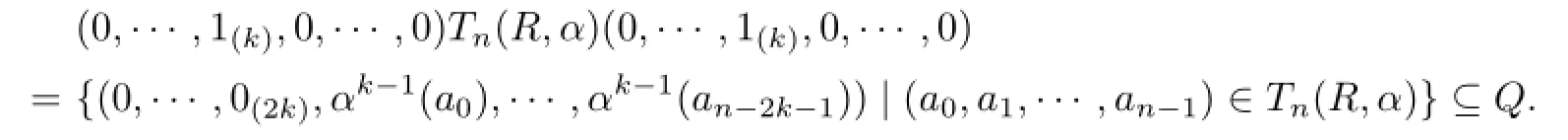
Continuing in this way,then after k-1 steps,we obtain
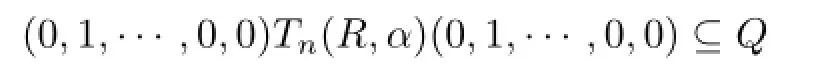
and hence(0,1,···,0,0)∈Q.
Let
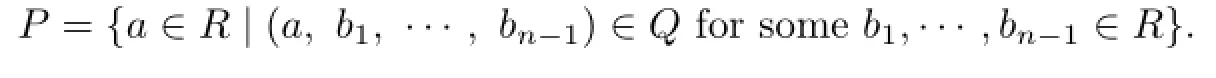
Then P is an ideal of R.Since(0,1,···,0),···,(0,···,1,0),(0,0,···,1)∈Q,
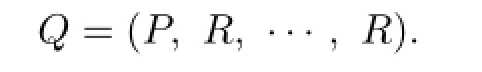
We show now that P is a strongly prime ideal of R.
Assume that x/∈Q0.Then(x,0,···,0)/∈Q,and hence there is a finite subset F of ((x,0,···,0))=((x),0,···,0)such that for all z∈Tn(R,α),Fz⊆I implies z∈I.This implies that there is a finite subset F0of(x)such that for all z0∈R,F0z0⊆P implies z0∈P.So P is a strongly prime ideal of R.
Conversely,assume that Q=(P,R,···,R)with P is a strongly prime ideal of R.Then Q=(P,R,···,R)is an ideal of Tn(R,α).For any x=(a0,a1,···,an−1)/∈Q,we have a0/∈P.Then there is a finite subset F of(a0)such that for all z∈R,Fz⊆P implies z∈P.Hence there is a finite subset¯F=(F,0,···,0)of(x)=((a0),∗,···,∗)such that for all¯z∈Tn(R;α),¯F¯z⊆Q implies¯z∈(P,R,···,R)=Q,where(x)is the ideal generated by x in Tn(R,α).So Q is a strongly prime ideal of Tn(R,α).
(3)It is similar to the proof of(1).
Proposition 3.3Let α be a nonzero endomorphism of R with α(1)=1.Then for any n≥1,we have
(1)sr(Tn(R,α))=(sr(R),R,···,R);
(2)sr(R[x;α]/(xn))=sr(R)+Rx+···+Rxn−1+(xn);
(3)us((Tn(R,α)))=us(R)+Rx+···+Rxn−1+(xn);
(4)us(R[x;α]/(xn))=us(R)+Rx+···+Rxn−1+(xn).
Recall that an ideal I of a ring R is a 2-primal ideal if Nil∗(R/I)=nil(R/I).Shin[12]showed that the following are equivalent in a ring R:
(1)every prime ideal of R is completely prime;
(2)every ideal of R is 2-primal ideal(see[12],Proposition 1.13).We usefor the class of all rings which satisfy these conditions.For any ring R,Birkenmeier et al.[13]defined(R)to be the sum of all ideals I of R such that I∈and called R to be-ring if R=(R).is an Amitsur-Kurosh radical property and is called generalized prime radical.
Proposition 3.4Let α be a nonzero endomorphism of R with α(1)=1.Then for any ideal P of R with P∈,
(2)Q=P+Rx+···+Rxn−1+(xn)∈.
Proof.Suppose Q=(P,R,···,R),where P is an ideal of R with P∈R2.Then Q is an ideal of Tn(R,α).Let I=(I0,I1,···,In−1)be a prime ideal of Q.Then I0is a prime ideal of P,and hence is a completely prime ideal of P since P∈.On the other hand,for e0=(0,0,···,1),e1=(0,0,···,1,0),···,en−1=(0,1,···,0,0)∈Q,(0,0,···,1)Q(0,0,···,1)=0⊆I implies that(0,0,···,1)∈I.Analogous to the proof of Proposition 3.2,we can obtain that(0,0,···,1)∈I,(0,···,0,1,0)∈I,···,(0,1,0,···,0)∈I.Thus I=(I0,R,···,R).Since I0is a completely prime ideal of P,for any x=(a0,a1,···,an−1),y=(b0,b1,···,bn−1)∈Q with xy∈I,we have a0∈I0or b0∈I0,and hence x∈I or y∈I.So I is a completely prime ideal of Q.It shows that Q∈.
Proposition 3.5Let α be a nonzero endomorphism of R with α(1)=1.Then for any n≥1,we have
Proof.By Proposition 3.4 we have
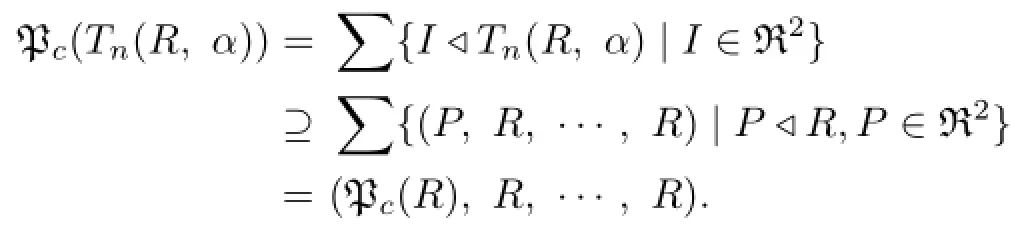
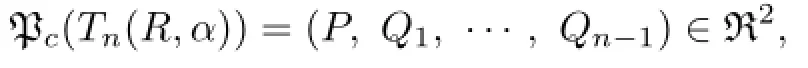
where Q1,···,Qn−1⊆R and P is an ideal of R.So
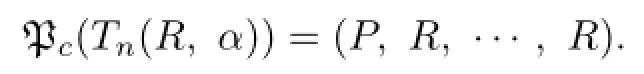
By Proposition 3.6 of[13],we know that
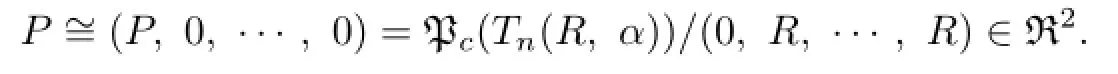
This implies that P⊆Pc(R),and hence
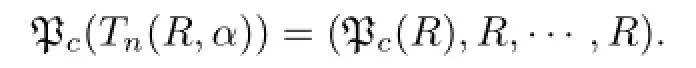
Recall that a ring is Brown-McCoy radical if and only if it cannot be homomorphically mapped onto a ring with unity or,equivalently,onto a simple ring with unity.A ring is called Behrens radical if it cannot be homomorphically mapped onto a ring with a nonzero idempotent or,equivalently,onto a subdirectly irreducible ring whose heart contains a nonzero idempotent.Beidar and Fong[14]proved that a ring is Behrens radical if and only if every left ideal of the ring is Brown-McCoy radical(see[14],Proposition 3.1).We denote by β the class of Behrens radical rings and denote by β(R)the Behrens radical of a ring R. β(R)is the intersection of prime ideals I of R such that R/I is subdirectly irreducible with heart H/I containing nonzero idempotents,where H is a ideal of R containing I(see[8]). Behrens radical lies between the Jacobson and Brown-McCoy radicals(see[15]).In the following,we use freely the fact that an ideal Q of the ring Tn(R,α)is prime if and only if Q=(P,R,···,R)for some prime ideal P of R(see[5],Theorem 2.8).
Proposition 3.6For any ring R and n≥1,
(1)β(Tn(R,α))=(β(R),R,···,R);
(2)β(R[x;α]/(xn))=β(R)+Rx+···+Rxn−1+(xn).
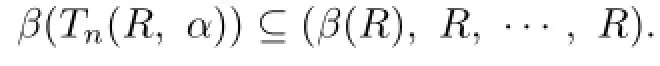
Proof.Suppose that P is a prime ideals of R such that R/P is subdirectly irreducible with heart H/P containing nonzero idempotent.Then Q=(P,R,···,R)is a prime ideal of Tn(R,α),and Tn(R,α)/QR/P implies thatOn the other hand,assume that Q is a prime ideals of Tn(R,α)such that Tn(R,α)/Q is subdirectly irreducible with heart containing nonzero idempotent.Then Q=(P,R,···,R),where P is a prime ideal of R.Since R/P∼=Tn(R,α)/Q,it follows that
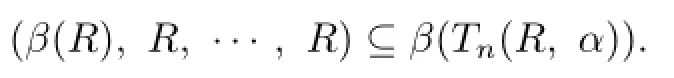
Therefore,
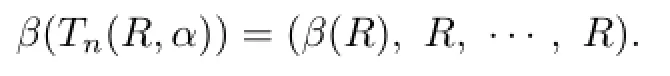
The proof is completed.
A ring R is called periodic if for each x∈R,there exist distinct positive integers m and n such that xm=xn.Bell and Klein[16]showed that periodicity is a special radical,the periodic radical P(R)of a ring R is the sum of all periodic ideals.Guo[17]proved thatwhere the intersection is taken over the set of prime ideals Iαsuch that R/Iαcontains no nontrivial periodic ideals(see[17],Theorem 1).A ring R is called N-nil if for each x∈R,there exist positive integers n and k such that nxk=0.The N-nil property is a radical property and the N-nil radical of a ring R,where the intersection is taken over the set of prime ideals Iαsuch that R/Iαcontains no nontrivial N-ideals.A ring R is called F-ring if for each a∈R,there exist a polynomial with integer coefficients f(x)=knxn+kn−1xn−1+···+k1x1such that f(a)=0.Wang and Yang[18]proved that F-ring property is also a radical property in the sense of Amitsur-Kurosh and the F-radical of a ring R,where the intersection is taken over the set of prime ideals Iαsuch that R/Iαcontains no nontrivial F-ideals.
Proposition 3.7For any ring R and n≥1,we have the following
(1)P(Tn(R,α))=(P(R),R,···,R);
(2)P(R[x;α]/(xn))=P(R)+Rx+···+Rxn−1+(xn);
(3)KN(Tn(R,α))=(KN(R),R,···,R);
(4)KN(R[x;α]/(xn))=KN(R)+Rx+···+Rxn−1+(xn);
(5)F(Tn(R,α))=(F(R),R,···,R);
(6)F(R[x;α]/(xn))=F(R)+Rx+···+Rxn−1+(xn).
Proof.(1)Assume that I is a prime ideals of R such that R/I contains no nontrivial periodic ideals.Then Q=(I,R,···,R)is a prime ideal of Tn(R,α).Since Tn(R,α)/Q∼=R/I,
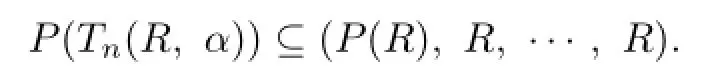
Conversely,Assume that Q is a prime ideals of Tn(R,α)such that Tn(R,α)/Q contains no nontrivial periodic ideals.Then there is a prime ideal I of R such that Q=(I,R,···,R). From R/I∼=Tn(R,α)/Q,we have
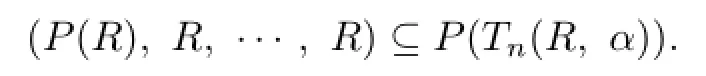
Therefore,

Similar to the proof of(1),we can obtain(3)and(5).
References
[1]Anderson D D,Camillo V.Armendariz rings and Gaussian rings.Comm.Algebra,1998,26(7): 2265–2272.
[2]Huh C,Kim H K,Kim N K,Lee Y.Basic examples and extensions of symmetric rings.J.Pure Appl.Algebra,2005,202(1):154–167.
[3]Kwak T K,Lee Y.Reflexive property of rings.Comm.Algebra,2012,40(4):1576–1594.
[4]Nasr-Isfahani A R,Moussavi A.On a quotient of polynomial rings.Comm.Algebra,2010,38(2):567–575.
[5]Nasr-Isfahani A R.On skew triangular matrix rings.Comm.Algebra,2011,39(11):4461–4469.
[6]Hong C Y,Kim H K,Kim N K,Kwark T,Lee K Y,Park K S.Rings whose nilpotent elements form a Levitzki radical ring.Comm.Algebra,2007,35(4):1379–1390.
[7]Karpilovsky G.The Jacobson radical of classical rings.in:Pitman Monographs&Surveys in Pure&Appl.Math.53,New York:Longman Scientific&Technical Wiley,1991.
[8]Watters J F.The Brown-McCoy radical and Jacobson rings.Bull.Acad.Polon.Sci.Ser.Sci. Math.Astronom.Phys.,1976,24(2):91–99.
[9]Antoine R.Nilpotent elements and Armendariz rings.J.Algebra,2008,319(8):3128–3140.
[10]Ouyang L Q.Ore extensions of weak zip rings.Glasgow Math.J.,2009,51(3):525–537.
[11]Olson D M.A uniformly strongly prime radical.J.Austral.Soc.(Ser.A),1987,43:95–102.
[12]Shin G Y.Prime ideals and sheaf representation of a pseudo symmetric rings.Trans.Amer. Math.Soc.,1973,184:43–60.
[13]Birkenmeier F,Heatherly H E,Lee E K.Completely prime ideals and associated radicals.in: S.K.Jain,S.T.Rizvi eds.Ring Theory(Granville,OH,1992),Singapore and River Edge: World Scientific,1993:102–129.
[14]Beidar K I,Fong Y.Polynomial rings over nil rings cannot be homomorphically mapped onto rings with nonzero idempotents.J.Algebra,2001,238(1):389–399.
[16]Bell H E,Klein A A.On rings with Engel cycles.Canad.Math.Bull.,1991,34(3):295–300.
[17]Guo X Z.On the periodic radical of a ring.Canad.Math.Bull.,1995,38(2):215–217.
[18]Wang Y,Yang J.The radical determined by P-property of rings.J.Math.Study,1999,32(5): 305–309.
10.13447/j.1674-5647.2016.03.08
date:Oct.3,2015.
The NSF(11071097,11101217)of China and the NSF(BK20141476)of Jiangsu Province of China.
*Corresponding author.
E-mail address:wweiliang@tju.edu.cn(Wang W L),wangyao@nuist.edu.cn(Wang Y).
 Communications in Mathematical Research2016年3期
Communications in Mathematical Research2016年3期
- Communications in Mathematical Research的其它文章
- Extended tanh-function Method for Solving Traveling Wave Solutions of Nonlinear Kundu Equation
- Existence of Multiple Positive Periodic Solutions for Second Order Differential Equations
- Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations
- A Class of Ruin Probability Model with Dependent Structure
- Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality
- Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching
