对一个条件恒等式的反思探究
杨宪立,纪保存
(1.河南教育学院 数学与统计学院,河南 郑州 450046;2.濮阳职业技术学院 数学与信息工程系,河南 濮阳 457000)
对一个条件恒等式的反思探究
杨宪立1,纪保存2
(1.河南教育学院 数学与统计学院,河南 郑州 450046;2.濮阳职业技术学院 数学与信息工程系,河南 濮阳 457000)
对一个条件恒等式进行了反思探究.利用牛顿公式,给出了一个条件恒等式的简捷证明,探究反思得到了4个类似的结论,从理论上对问题进行了探索论证并进行了推广,得到了9个新的命题.
恒等式;探究;命题;正整数数组
文献[1]中有这样一道题目:已知a1,a2,a3∈R,且a1+a2+a3=0,求证
(1)
这个简单的条件恒等式洋溢着对称、奇异、和谐、统一等数学美.如此优美的条件恒等式,自然引起了我们极大的兴趣,好奇心驱使我们进行反思:它是怎么得来的?还有类似的条件恒等式吗?能推广吗?
探究1探源与简证.
(1)式最初是何人给出,又是如何发现的,最早出现在何处,笔者手头缺乏资料,无从考证,只有大胆猜测,它与牛顿公式有关.即使猜测错误,至少利用牛顿公式也能给出(1)式的一个简捷证明.

1)当m≤k时,sm=σ1sm-1-σ2sm-2+…+(-1)mσm-1s1+m(-1)m+1σm;
2)当m>k时,sm=σ1sm-1-σ2sm-2+…+(-1)k+1σksm-k.
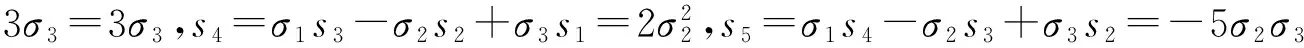
从以上证明中还可得出以下命题1.
命题1已知a1,a2,a3∈R,且a1+a2+a3=0,求证
探究2还有与(1)式类似的恒等式吗?
继续利用牛顿公式计算:


由此,可得
命题2已知a1,a2,a3∈R,且a1+a2+a3=0,求证

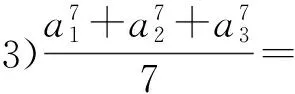
(2)
探究3观察结构上完全一致的(1)式和(2)式,可统一表示为

(3)
那么,使(3)式恒成立的正整数数组(m,n)有几组解呢?
因为a1+a2+a3=0,所以a3=-(a1+a2),从而(3)式等价于
(4)

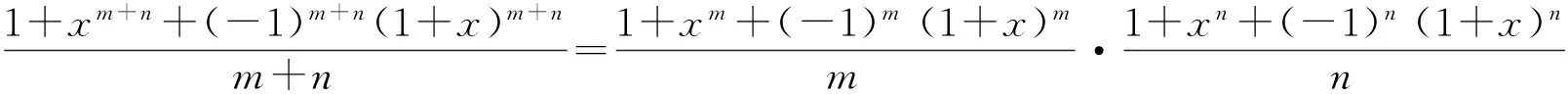
(5)



(6)
可以验证,当n=3时,(6)式左右两边相等,所以(2,3)是所求的一组解.

综上所述,可得命题3.
命题3已知a1,a2,a3∈R,且a1+a2+a3=0,则使(3)式恒成立的正整数数组(m,n)(m≤n)只有两组解(2,3)与(2,5).
探究4(1)式的推广.
命题4设a1,a2,a3,a4∈R,且a1+a2+a3+a4=0,求证

命题5设a1+a2+a3+a4=0,则使f4(m+n)=f4(m)f4(n)恒成立的正整数数组(m,n)(m≤n)只有一组解(2,3).


证明当a5=a6=……=ak=0时,命题6化为命题5,因此它最多只有一组解(2,3).取a1=a2=a3=1,a4=-1,a5=-2,a6=a7=……=ak=0,则fk(2+3)=-6,fk(2)fk(3)=-8,从而(2,3)不是它的解,故命题成立.
限于篇幅,下面3个命题的证明略去,有兴趣的读者可自证.
命题7设a1+a2+a3=0,则使f3(m+n+t)=f3(m)f3(n)f3(t)(m≤n≤t)恒成立的正整数数组(m,n,t)只有一组解(2,2,3).
命题8设a1+a2+…+ak=0(k≥4),则不存在正整数数组(m,n,t),使fk(m+n+t)=fk(m)fk(n)fk(t)恒成立.
命题9设a1+a2+…+ak=0(k≥3),则不存在正整数数组(m1,m2,…,mr)(r≥4),使fk(m1+m2+…+mr)=fk(m1)fk(m2)…fk(mr)恒成立.
[1]李长明,周焕山.初等数学研究[M].北京:高等教育出版社,1995:127.
[2]余希元,田万海,毛宏德.初等数学研究:上[M].北京:高等教育出版社,1988:163.
The Reflection and Inquiry on a Conditioned Identity
YANG Xianli1, JI Baocun2
(1.School of Mathe matics and Statistics, Henan Institute of Education, Zhengzhou 450046, China;2.Department ofMethematicsandStatistics,PuyangVocationalandTechnicalCollege,Puyang457000,China)
The inquiry and reflection were made on a conditioned identity. And gives a succinct proof with the help of Newton formula. What’s more, probes into four similar conclusions, and demonstrates the problem theoretically. In addition, popularizes the problem and gets nine new propositions.
identity; inquiry; proposition; positive integer array
2016-04-16
河南省高等学校重点科研项目(16B110005);河南省教育厅教师教育改革研究项目(2015-JSJYYB-120)
杨宪立(1961—),男,河南林州人,河南教育学院数学与统计学院教授,主要研究方向:数学教育.
10.3969/j.issn.1007-0834.2016.03.013
G642
A
1007-0834(2016)03-0046-03

