脐带缆在潜器下放过程中的运动建模与仿真

李霄霄，马 宁，刘 晗，顾解忡

(1.上海交通大学 海洋工程国家重点实验室，上海 200240; 2.高新船舶与深海开发装备协同创新中心，上海 200240)

脐带缆在潜器下放过程中的运动建模与仿真

李霄霄1,2，马 宁1,2，刘 晗1,2，顾解忡1,2

(1.上海交通大学 海洋工程国家重点实验室，上海 200240; 2.高新船舶与深海开发装备协同创新中心，上海 200240)

潜器在下放布置过程中需要考虑变长度的脐带缆对其运动的影响，在考虑流的情况下，对脐带缆的有限差分模型进行了改进，并采用最小二乘方法求解由时间和空间上的中心差分格式离散后的非线性方程组。为了验证模型改进的有效性，将潜器在均匀定常流中水平匀速直航时的数值解与该特殊情况下的解析解进行比较，两组解的吻合不仅证实了模型改进的有效性，而且表明上述数值计算方法是可靠且有效的。在潜器下放布置运动给定的情况下，脐带缆的运动仿真结果表明，潜器姿态角的调整会对拖曳点处的缆绳张力大小和变化趋势产生显著的影响，流在改变缆绳空间形状的同时引起了缆绳对潜器作用力和力矩的非线性和时变性，脐带缆总是阻止潜器自身动力对运动速度和姿态角的改变，且对纵荡运动的影响最大。

水下潜器；变长度脐带缆；有限差分法；最小二乘法；均匀定常流

Abstract:With consideration of current,the finite difference model for umbilical cable is improved to evaluate the effects of variable-length cable on underwater vehicle’s motion during its deployment.The least square method is adopted to solve the nonlinear equations discretized with central-difference scheme over time and space.The validity of the improved model is verified by comparing the numerical solution with the analytical one when the underwater vehicle is horizontally moving forward with a constant velocity in uniform steady flow.The agreement between numerical solutions and analytical ones not only confirms the validity of the improved model but also proves the reliability and validity of the numerical scheme.For the condition that the deployment motion of the underwater vehicle is given,the simulation results of the umbilical cable motion indicate that the adjustment of the underwater vehicle’s attitude angle can significantly affect the value and variation tendency of cable tension at tow-point.The existence of current causes the nonlinearity and time-dependency of force and moment acting on the underwater vehicle while changing the configurations of cable.Moreover,the umbilical cable always hinders the change of the underwater vehicle’s velocity and attitude angle powered by itself,and surge motion is most affected by the cable.

Keywords:underwater vehicles; length-variable umbilical cable; finite difference method; least square method; uniform steady flow

随着海洋工程的不断发展，带缆水下潜器的应用越来越多，也越来越受到研究者的重视，特别是拖曳系统动力学问题成为研究的热点。目前，关于拖缆的动力学问题主要采用有限差分法[1-2]和集中质量法[3-4]来求解。早些年的研究主要集中于定长度的拖缆[5-6]，对于变长度缆的研究较少。近些年，关于变长度缆问题的研究越来越多，Feng Z[7]采用有限差分法计算了信息缆对水下航行器运动的影响，卢军[8]采用有限差分法对水下拖曳系统的收放安全性进行了模拟计算；王飞、徐刚[9-10]等采用集中质量法对收放缆速度为已知函数的拖缆收放问题进行了研究，但计算结果有些扰动，杨智栋[11]等采用集中质量法对变长度拖缆AUV的纵向运动进行了建模与仿真。

本文基于有限差分模型，对考虑流作用下的现有数学模型进行了一定的改进，并采用最小二乘法求解离散后的非线性方程组。为了验证模型改进与最小二乘方法的有效性，将潜器在均匀定常流中匀速水平直航这一特殊情况的数值结果与解析解进行了对比，使这种有效性得到了验证。文中还对潜器下放布置过程中的下潜与转动运动进行了仿真计算，并给出了脐带缆的空间形状变化及其对潜器运动的影响。

1 变长度缆的运动建模

整个系统如图1所示，由水面母船、传输信号的脐带缆和水下潜器ARV组成。考虑到水面母船的质量相对于脐带缆和水下潜器大很多，可以认为脐带缆传递给水面母船的张力不会使母船产生相应的运动，因此整个系统的运动就集中于脐带缆和水下潜器上。下面给出变长度脐带缆的运动建模过程。

1.1坐标系的建立及坐标变换关系

在图1中，建立三个坐标系：船体固定的整体坐标系i-j-k、脐带缆局部坐标系t-n-b和潜器局部坐标系iv-jv-kv。

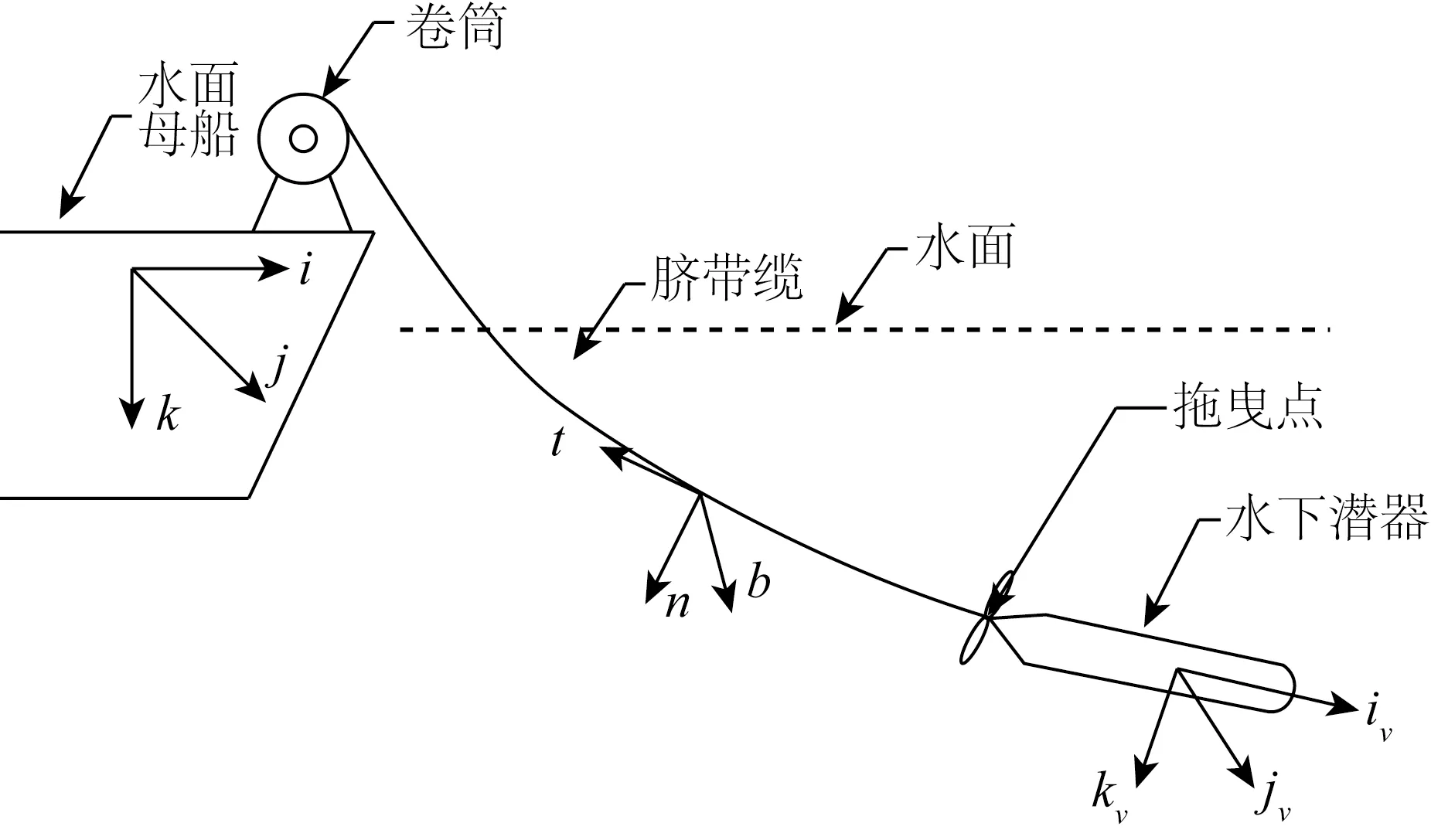
图1 坐标系示意Fig.1 Coordinate system

潜器局部坐标系与整体坐标系之间的变换关系为[12]：

脐带缆局部坐标系与整体坐标系之间的变换关系为[2]：

根据式(1)～(3),可以得到缆绳局部坐标系与潜器局部坐标系之间的变换关系：

1.2脐带缆的动力平衡方程式

假定脐带缆是具有圆形横截面的细长柔性柱体。脐带缆在水中运动时，要受到重力、浮力、流体阻力、惯性力以及水面母船和水下潜器的拉力作用，取单位微元的脐带缆进行受力分析，可以得到脐带缆的动力平衡方程式：

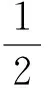
同时考虑到脐带缆在运动过程中，缆形变化是连续光滑的，则有缆的连续性方程：

式(6)中右边部分的上角标表示对未拉伸状态时缆绳长度s的偏导数。

联立矢量方程(5)、(6)，并设未知矢量Y=[T,Vt,Vn,Vb,α,β]T，通过推导化简，可以将上述矢量方程组写成如下的矩阵形式：

式中：e=1/EA，m1=m0+ρA0，wc=(m0-ρA0)g，N1=-ρA0(Jxcosα-Jysinα)，N2=-ρA0(Jxsinαsinβ+Jycosαsinβ)，N3=-ρA0(-Jxcosαcosβ+Jysinαcosβ+Jzsinβ) 。

1.3边界条件

在整个系统中，脐带缆的边界条件由两部分组成，一部分是脐带缆首端边界条件，即在缆绳与水下潜器的连接点处的速度应保持连续性：

式中：Vc=[u,v,w]、Ωc=[p,q,r]、rc=[xc,yc,zc]分别为潜器局部坐标系下潜器的线速度、角速度和连接点处的位置坐标。

另一部分是脐带缆尾端边界条件，缆绳在该处与水面母船上的缆绳卷筒相连接，此时缆绳仅有切向速度，而无法向速度，同时考虑到卷筒角动量随时间的变化，可以得到如下的边界方程[7]：

式中：Rd、Id为卷筒的半径、转动惯量，Γf为转轴处的阻尼力矩。

1.4脐带缆对潜器的作用力与作用力矩

由拖曳点处的缆绳张力T(0,t)，经过坐标变换可以得到在潜器局部坐标系下，缆绳作用于水下潜器上的作用力和作用力矩：

2 数值计算方法

鉴于脐带缆的控制方程是一个复杂的偏微分方程，为此采用空间和时间的中心差分方法将方程离散，并采用最小二乘法求解离散后的非线性方程组。

2.1控制方程的离散——有限差分法

同时定义如下的离散形式[7]：

在式(15)中，由于新微段ΔSk+1在tk时未浸没于水中，需要根据卷筒的转动对tk时的未知矢量Y(Sk+1,tk)进行假定，这里假定Y(Sk+1,tk)=[T(Sk,tk),Vt(Sk,tk),0,0,α(Sk,tk),β(Sk,tk)]，与文献[7]的假定略有不同，且数值计算结果表明这种假定是合理的。

在节点(Sj-1/2,tk+1/2),j=1,2,...,k+1离散控制方程(7)，可以得到如下6(k+1)个差分方程[2]：

边界方程(8)～(11)的离散形式如下：

2.2数值求解流程

式(16)～式(20)构成一个含有6(k+2)个非线性方程的方程组，且随着时间t的变化，非线性方程个数和未知数个数都发生相应的变化。上述非线性方程组的求解采用最小二乘法，数值求解流程如下：

图2 数值求解流程Fig.2 Flow chart of numerical computation

3 仿真结果与分析

脐带缆为细长的轻缆，且所受浮力大小等于重力，其连接于水下潜器的位置坐标为rc=[-0.6,0,0]；卷筒的半径为0.1 m，且忽略转轴处的阻尼力矩Γf，缆绳和流体参数[7]如下：

表1 缆绳和流体参数Tab.1 Cable and fluid parameters

3.1水平匀速直航

由于脐带缆为中性浮力的轻缆，在水下潜器水平匀速直航，且水流速度J与潜器运动方向平行的情况下，缆绳在每一节点处的欧拉角α、β以及速度Vt、Vn、Vb均不随时间t和缆绳长度s的变化，控制方程(7)可化简为：

由边界方程(9)可求得上式的解析解如下：

由式(14)，可进一步得到缆绳在潜器拖曳点处的张力(缆绳对潜器的拖曳阻力)：

取时间步长Δt=1 s，仿真时间TIME=50 s，水下潜器的运动参数为：u=2 m/s，v=w=0，p=q=r=0，φ=θ=ψ=0；根据文献[13]中关于南海北部海流的观测结果，水流速度分别取为：Jx=Jy=Jz=0、Jx=-0.1 m/s,Jy=Jz=0和Jx=-0.2 m/s,Jy=Jz=0。在不同流速下，拖曳点处缆绳张力的数值计算结果和解析解如图3所示。

由图3可以看出，随着时间的增加，缆绳长度不断增加，拖曳点处缆绳张力也以近乎线性的方式增加，出现这样现象的主要原因是水对缆绳的阻力随着缆绳长度增加而不断增加；比较不同流速时拖曳点处的缆绳张力，可以发现流对张力的影响明显，且这种影响随着时间增加而不断增大；比较各流速时数值计算结果和解析解，可以看出数值结果与解析解吻合良好，这也间接证明了模型改进以及最小二乘方法求解非线性方程组的有效性。

3.2定角速度下潜与转动

图4分别给出了潜器在该运动过程中纵倾角θ与首向角ψ随时间的变化规律。

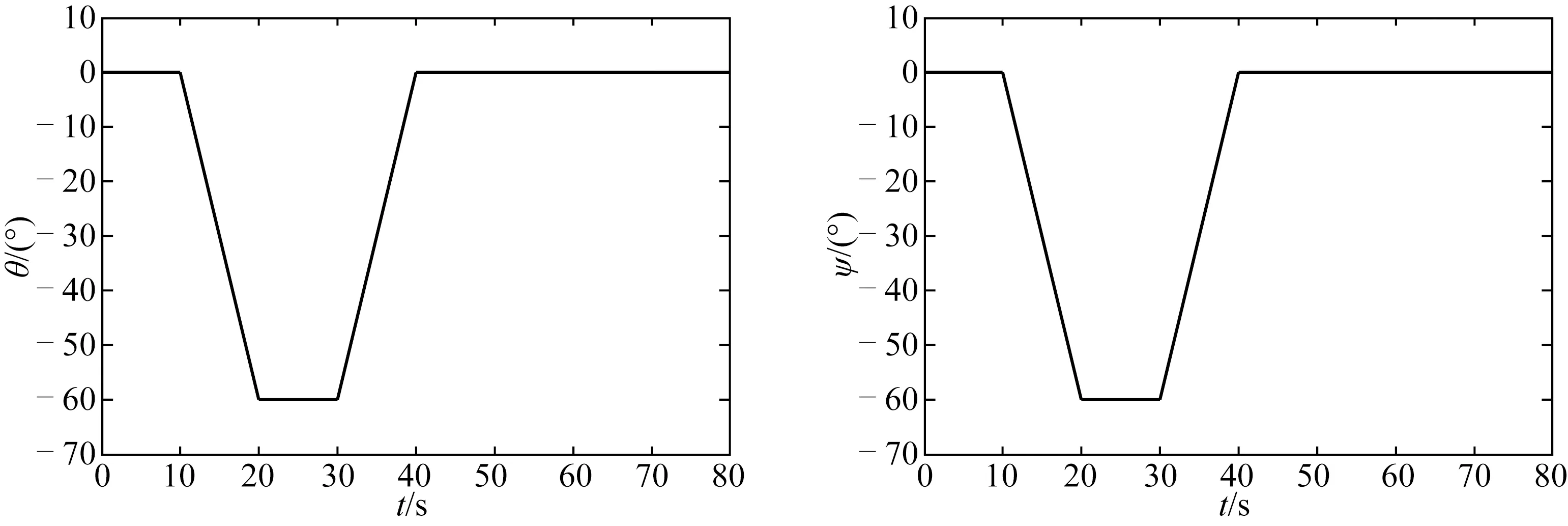
图4 潜器在不同时刻的纵倾角和首向角Fig.4 Pitch angles and heading angles at different time

图5分别给出了脐带缆在0～40 s、40～80 s两段时间内空间形状的变化，左侧图表明潜器正在逐渐下潜，右侧图表明潜器正逐渐转向，且由左侧图可以看出Jy=0.1 m/s的流使脐带缆沿y的正向有明显的偏移，且计算结果表明最大偏移位置约为y=3 m。

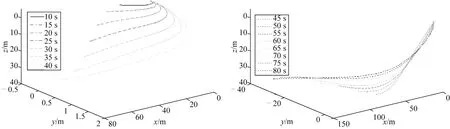
图5 不同时刻的缆形变化Fig.5 Configurations of cable at different time

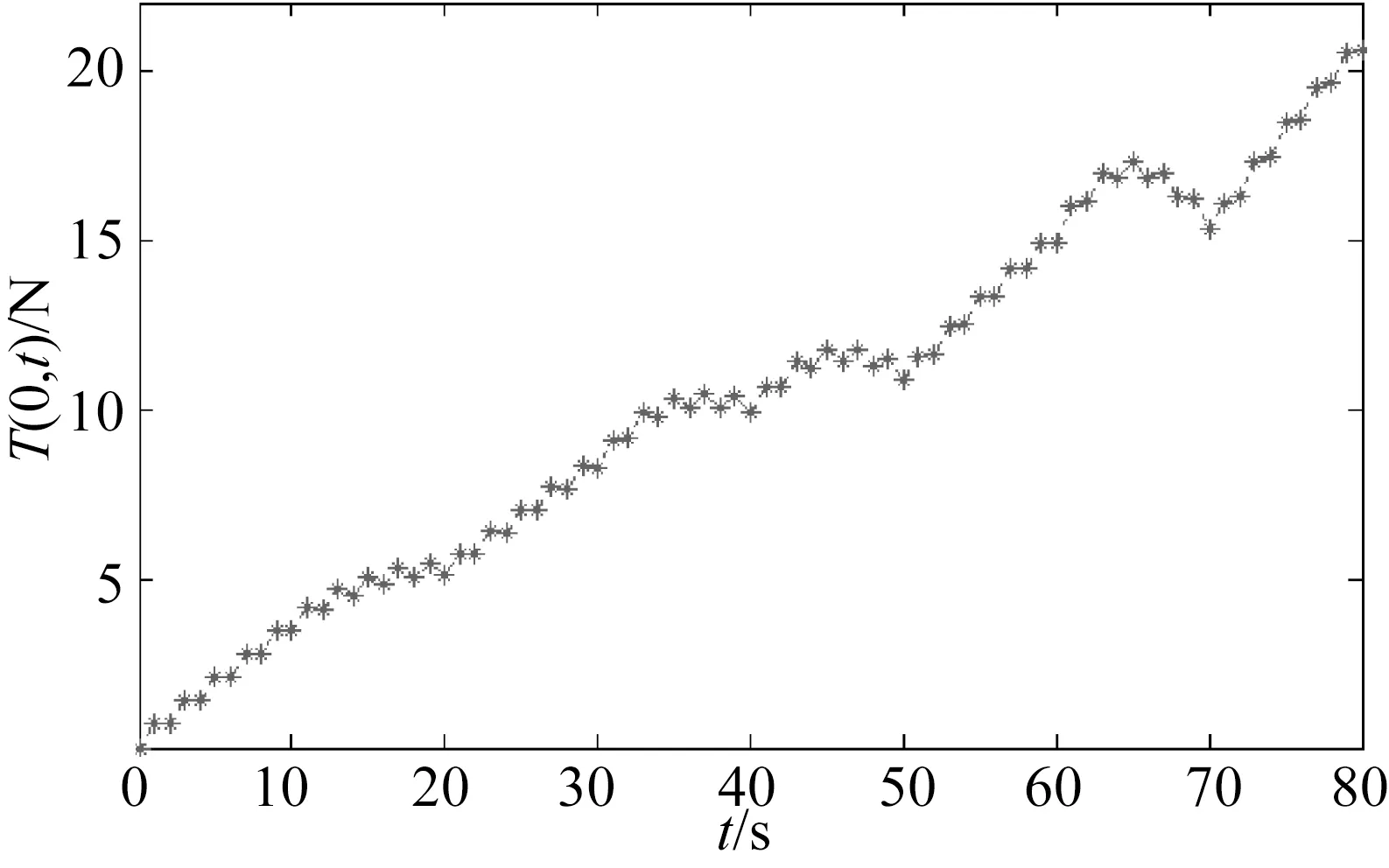
图6 拖曳点处缆绳张力随时间的变化Fig.6 Variation of cable tension at tow-point with time

图6表明拖曳点处脐带缆的张力T(0,t)总体上是随时间不断增大的，仅在30～40 s,40～50 s,60～70 s三个时间段内出现小幅的先增后减的趋势，其余时间段内基本上呈线性增大的趋势，出现上述情况的主要原因是潜器在这三个时间段内由纵倾角θ=-60°调整为无纵倾，首向角ψ=-60°调整为无首向角，使得拖曳点处的速度Vn、Vb出现方向更替，导致脐带缆与潜器之间的作用力呈现微幅的先增后减趋势。

图7给出了拖曳点处脐带缆在缆绳局部坐标系下三个方向的运动速度，从图中可以看出切向速度Vt出现微幅的波动，但基本保持在-2 m/s左右，速度Vn随着纵倾角θ的变化而发生从0 m/s到0.5 m/s到-0.5 m/s再到0 m/s的变化，速度Vb随着首向角ψ的变化也发生与Vn类似的变化。

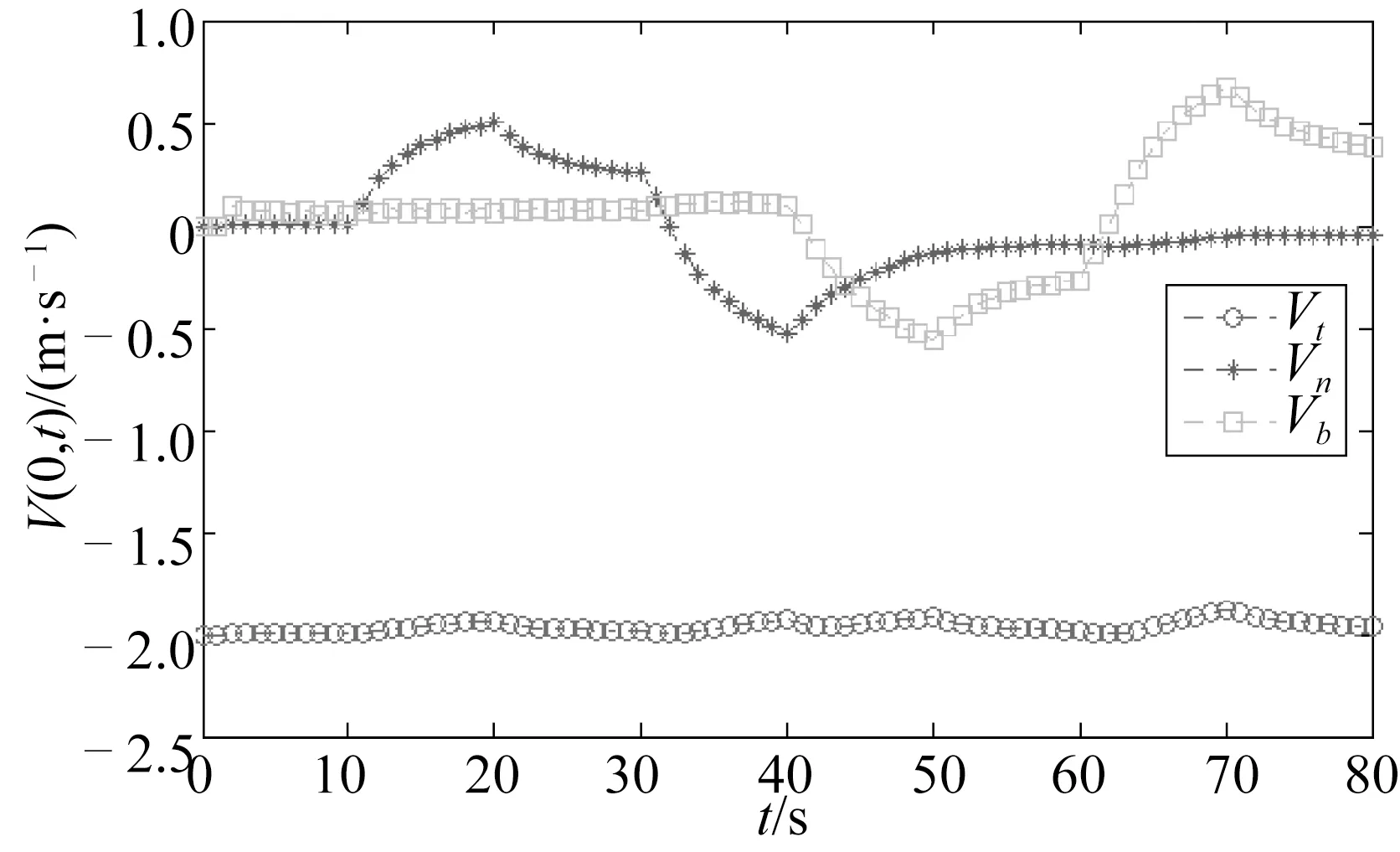
图7 拖曳点处缆绳速度随时间的变化Fig.7 Variation of cable velocities at tow-point with time

图8分别给出了在潜器局部坐标系下脐带缆对潜器的作用力Fc和作用力矩Mc，由左侧图可以看出Fcx的大小一直在增加，表明若推进器的功率保持不变，则潜器的前进速度将不断减小，Fcy,Fcz分别随首向角ψ和纵倾角θ的变化在正向、负向和零之间变化，从而产生横向加速度和垂向加速度来改变潜器的运动状态；由右侧图可以看到Mcx始终保持零值，从而保证潜器不会发生横摇，而这一结果也与实际情况相吻合，Mcy,Mcz分别随纵倾角θ和首向角ψ的变化也在正向、负向和零之间变化，从而使潜器不断调整纵倾角θ和首向角ψ，来达到预设的潜器姿态角。

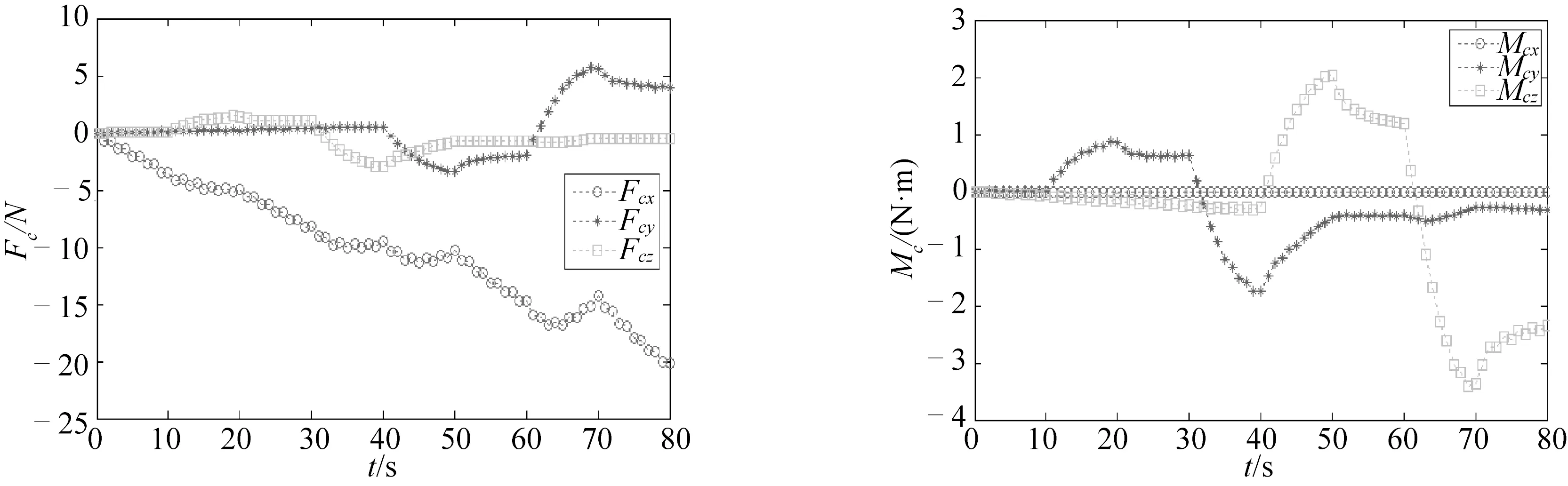
图8 缆绳在不同时刻对潜器的作用力和作用力矩Fig.8 Force and moment acting on underwater vehicle by cable at different time

4 结 语

在考虑定常均匀流的情况下，通过脐带缆的运动建模对原有的有限差分模型进行了改进，并进行了潜器在下放布置过程中的脐带缆运动数值模拟，在潜器运动过程给定的情况下得到如下结论：

1)虽然拖曳点处的缆绳张力总体上随着缆绳浸水部分的增加呈线性增大的趋势，但潜器调整姿态角的过渡运动时间段内缆绳张力呈缓慢的先增后减趋势，因此潜器姿态角的调整对拖曳点处缆绳张力变化趋势所产生的影响不可忽略。

2)流速的增加不仅使拖曳点处的缆绳张力增大，而且流的存在会改变缆绳的空间形状，特别是会使缆绳发生显著的横向位置偏移；流的存在增强了缆绳作用于潜器的力和力矩的非线性和时变性，给潜器的操纵带来更大的困难，因此在潜器下放布置时，应选择流对缆绳运动影响最小的路径下放潜器。

3)脐带缆作用于潜器的力和力矩总是阻止潜器自身动力对运动速度和姿态角的改变，且对纵荡运动的影响比其他运动的影响更大，需要在潜器的设计和运动控制中对该类运动给予最大的关注。

[1] ABLOW C M,SCHECHTER S.Numerical simulation of undersea cable dynamics [J].Ocean Engineering,1983,10 (6):443-457.

[2] MILINAZZO F,WILKIE M,LATCHMAN S A.An efficient algorithm for simulating the dynamics of towed cable systems [J].Ocean Engineering,1987,14 (6):513-526.

[3] WALTON T S,POLACHECH H.Calculation of transient motion of submerged cables [J].Mathematics of Computation,1960,14:27-46.

[4] HUANG S.Dynamic analysis of three-dimensional marine cables [J].Ocean Engineering,1994,21 (6):587-605.

[5] WU Jiaming.Simulation of a two-part underwater towed system [D].Pokfulam,Hong Kong:The University of Hong Kong,1998.

[6] 李英辉,李喜斌,戴杰,等.拖曳系统计算中拖缆与拖体的耦合计算[J].海洋工程,2002,20(4):37-42.(LI Yinghui,LI Xibin,DAI Jie,et al.Calculation of coupling between the cable and the towed-body in the towed system [J].The Ocean Engineering,2002,20(4):37-42.(in Chinese))

[7] FENG Z,ALLEN R.Evaluation of the effects of the communication cable on the dynamics of an underwater flight vehicle [J].Ocean Engineering,2004,31(8-9):1019-1035.

[8] 卢军,黄国樑.水下拖曳系统收放安全性的模拟计算[J].上海交通大学学报,2005(5):691-694+700.(LU Jun,HUANG Guoliang.Numerical calculation of the security of deploying and retracting underwater towed system [J].Journal of Shanghai Jiaotong University,2005(5):691-694+700.(in Chinese))

[9] 王飞.海洋勘探拖曳系统运动仿真与控制技术研究[D].上海:上海交通大学,2007.(WANG Fei.Simulation and control research of marine towed seismic system [D].Shanghai:Shanghai Jiaotong University,2007.(in Chinese))

[10] 徐刚,葛彤,朱继懋,等.“海龙-3500”深海潜水器的变长缆运动建模与仿真[J].造船技术,2005(5):26-30+25.(XU Gang,GE Tong,ZHU Jimao,et al.Motion modeling and simulation of "Sea-Dragon 3500" ROV with variable length cables[J].Marine Technology,2005(5):26-30+25.(in Chinese))

[11] 杨智栋,潘光,杜晓旭.变缆长拖缆AUV纵向运动建模与仿真[J].鱼雷技术,2014(1):14-19.(YANG Zhidong,PAN Guang,DU Xiaoxu.Longitudinal motion modeling and simulation of tethered AUV with length-variable towing cable [J].Torpedo Technology,2014(1):14-19.(in Chinese))

[12] FOSSEN T I.Guidance and control of ocean vehicles [M].Chichester:John Wiley & Sons,1994:9-12.

[13] 杨庆轩,梁鑫峰,田纪伟,等.南海北部海流观测结果及其谱分析[J].海洋与湖沼,2008(6):561-566.(YANG Qingxuan,LIANG Xinfeng,TIAN Jiwei,et al.Observation of the current in the Northern South China Sea and spectrum analysis [J].Oceanologia Et Limnologia Sinica,2008(6):561-566.(in Chinese))

Motion modeling and simulation of umbilical cable during underwater vehicle’s deployment

LI Xiaoxiao1,2,MA Ning1,2,LIU Han1,2,GU Xiechong1,2

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; 2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE),Shanghai,200240,China)

P75.1

A

10.16483/j.issn.1005-9865.2016.02.007

1005-9865(2016)02-0047-09

2015-01-19

国家重点基础研究发展计划(973计划)资助项目(2014CB046806-003)

李霄霄(1989-)，男，山东枣庄人，硕士研究生，主要从事海洋工程水动力性能研究。E-mail:cangqiong@mail.sjtu.edu.cn