海底管线整体屈曲过程中塑性变形研究
闫澍旺,洪兆徽,闫 玥,刘文彬
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.中交天津港湾工程研究院有限公司,天津 300222)
海底管线整体屈曲过程中塑性变形研究
闫澍旺1,洪兆徽1,闫 玥1,刘文彬2
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.中交天津港湾工程研究院有限公司,天津 300222)
海底管线是海洋油气工程中主要的输送手段。在工作状态下,受高温高压的影响,深海管线可能会发生水平向整体屈曲。随海洋油气作业水深的增大,施加于管线的温度和压强也逐渐增加,导致管线产生较大的屈曲位移和截面应力,使得截面产生塑性应变。本文采用数值模拟方法,对海底管线整体屈曲过程中塑性区的分布及其与整体屈曲影响因素的关联性、塑性变形对水平向变形的影响和塑性变形造成的截面椭圆度的变化规律进行分析,研究塑性变形对整体屈曲过程影响的规律。
海底管线;水平向整体屈曲;塑性变形;椭圆度
Abstract:Submarine pipeline is widely used in offshore oil and gas development engineering.The deep-water pipeline may have lateral global buckling due to the high temperature and pressure.With the increasing operating water depth,pipeline suffers higher temperature and pressure difference,leading to larger buckling displacement and plastic deformation.Tthe influence of plastic deformation on the pipeline global buckling process is studied using numerical simulation method.The distribution of plastic deformation region and the interaction between plastic strain and lateral global buckling influence factors are analyzed.The impact of plastic deformation on the lateral displacement and the ovality caused by the plastic deformation are calculated to reveal the influence of the plastic deformation on the lateral global buckling.
Keywords:submarine pipeline; lateral global buckling; plastic deformation; ovality
海洋油气工程中,经济、高效、安全的海底管线系统是油气资源运输最主要的手段。在运输油气资源的过程中,受到高温高压的影响,海底管线产生较大的温度应力,由于海床对海底管线的约束,热应力不能通过自由膨胀得到释放。对于深海管线,常常直铺于海床上,管线受到的水平向土体约束力较小,逐渐累积的应力最终导致管线发生水平向的大变形,称为海底管线的水平向整体屈曲。
海底管线整体屈曲的研究始于5种理想管线屈曲形态的提出[1],随后Taylor和Gan[2]在此基础上,对带初始缺陷管线的低阶模态的整体屈曲进行了分析。2005年,刘润等[3]结合实际工程改进了管线屈曲变形的计算方法,分析了温差、地基土特性、管线埋深和膨胀弯设置等因素对管线屈曲变形的影响。2010年,Antunes推导[4]了含浮力模块管线的整体屈曲解析解,揭示了含浮力模块的海底管线发生整体屈曲的变形特性。2014年,LIU运用[5]能量法推导了理想管线发生高阶模态整体屈曲的解析解,分析了温度应力、管线截面刚度、地基土特性以及干扰力对管线整体屈曲的影响。2015年Hong等[6]对缺陷管线发生3阶模态屈曲进行了研究,并解释了经典解析解中“snap”的屈曲现象。2015年,洪兆徽等[7]对待双拱初始缺陷的管线发生第2阶和第4阶模态的整体屈曲过程进行了分析。
进入21世纪后随着数值计算软件的日益成熟,出现了大量针对海底管线整体屈曲的数值研究。2004年,Villarraga等[8]利用数值计算的方法研究了不同土体约束力下含初始缺陷埋设管线的竖直向整体屈曲变形过程。2006年,Cardoso等[9]采用有限元分析软件SIGMA研究了动态土体约束力模型对循环荷载作用下管线整体屈曲变形的影响。2008年,Rathbone等[10]运用有限元法分析了初始缺陷形态对管线水平向整体屈曲的影响规律,同时提出可以将初始缺陷管线视为一种跨度较小的蛇形铺管管线。2015年,Hong等[11]对温压联合作用下海底管线失效包络线进行了分析,并提出了相应的函数表达式。此外,Chee和Walker[12],Cumming等[13]也采用数值分析方法对海底管线整体屈曲过程中内力和变形规律进行了相应的分析。
在以往的研究中,针对塑性变形对整体屈曲影响的分析较少。但随着海洋油气开采逐渐向更深的海域进军,海底管线承受的温度和压强逐渐增大(例如墨西哥湾某项目的工作温度和压强分别达到了177 ℃和44.8 MPa[14]),受热屈曲后局部管线的应力也逐渐增加,管线随之产生的塑性应变也较大,需要开展管线塑性变形对整体屈曲影响的研究。同时,鉴于经典解析解方法仍广泛应用于海底管线设计的实践中,研究塑性应变的分布及其对整体屈曲变形的影响也能对经典解析解的适用性起到一定的修正作用。
1 数值分析方案
数值分析中采用动力隐式方法计算海底管线在高温高压下的整体屈曲,管线采用S4R单元模拟,每个截面分16个单元,沿管线轴向单元长度为0.5 m。管线钢材的重度取水下重度68.5 kN/m3,管线总计算长度为2 km,在管线中点处引入初始缺陷,计算时约束管线两端的水平向位移。地基土体采用C3D8R单元模拟,水平向分20个单元,每个单元的竖直向长度为0.5 m,每个单元沿轴向长度为1 m。土体浮重度为7.8 kN/m3,计算时约束土体四周的水平向位移和土体底面水平向和竖直向的位移。管线与土体间竖直向采用“硬”接触模拟,当两者相接触时传递正向的接触压力,两者分离时接触面脱开,相互作用力归零;管线与土体间水平向采用“罚”函数模拟,即水平向约束力大小与接触压力和约束力系数相关。分析中采用各向异性的约束力系数,分别设定侧向和轴向约束力系数的大小。数值计算模型如图1所示。
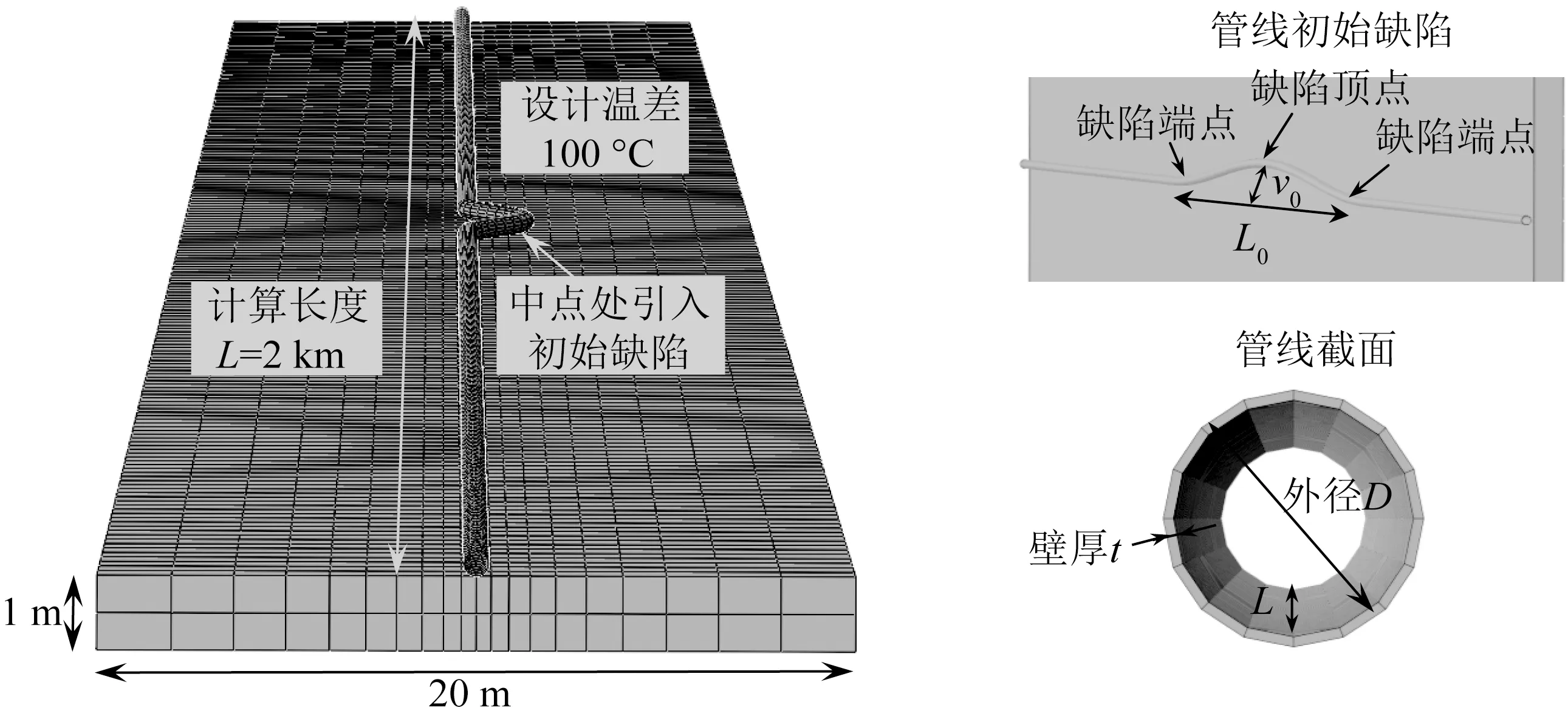
图1 管线整体屈曲数值计算模型Fig.1. Finite element analysis model for the simulation of pipeline global buckling
在数值分析过程中,选取钢材等级为X65的管线钢为代表,X65管线钢单向拉伸时应力应变曲线如图2所示。
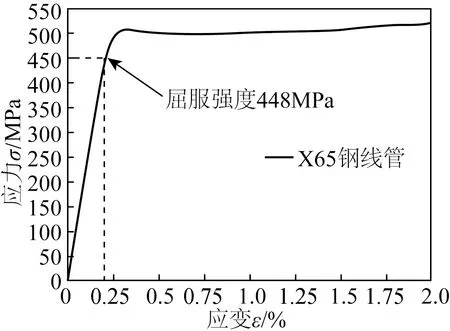
图2 X65管线钢单向拉伸时应力应变曲线Fig.2. The stress-strain curve for X65 pipeline steel under tension
在海底管线的整体屈曲分析中,管线的初始缺陷状态、所受压强差的大小、管线截面的参数、管线所受土体约束力大小等都会对管线的整体屈曲过程产生一定的影响,为使本文的分析结果更为可信,在研究中对整体屈曲影响因素(初始缺陷参数、压强差、截面参数和土体约束力系数),依次分别设计了9个、6个、7个和5个管线钢材为弹塑性的数值模型,并对每个影响因素同时分别设置1个管线钢材为线弹性的对比模型,具体的模型参数设计如下:
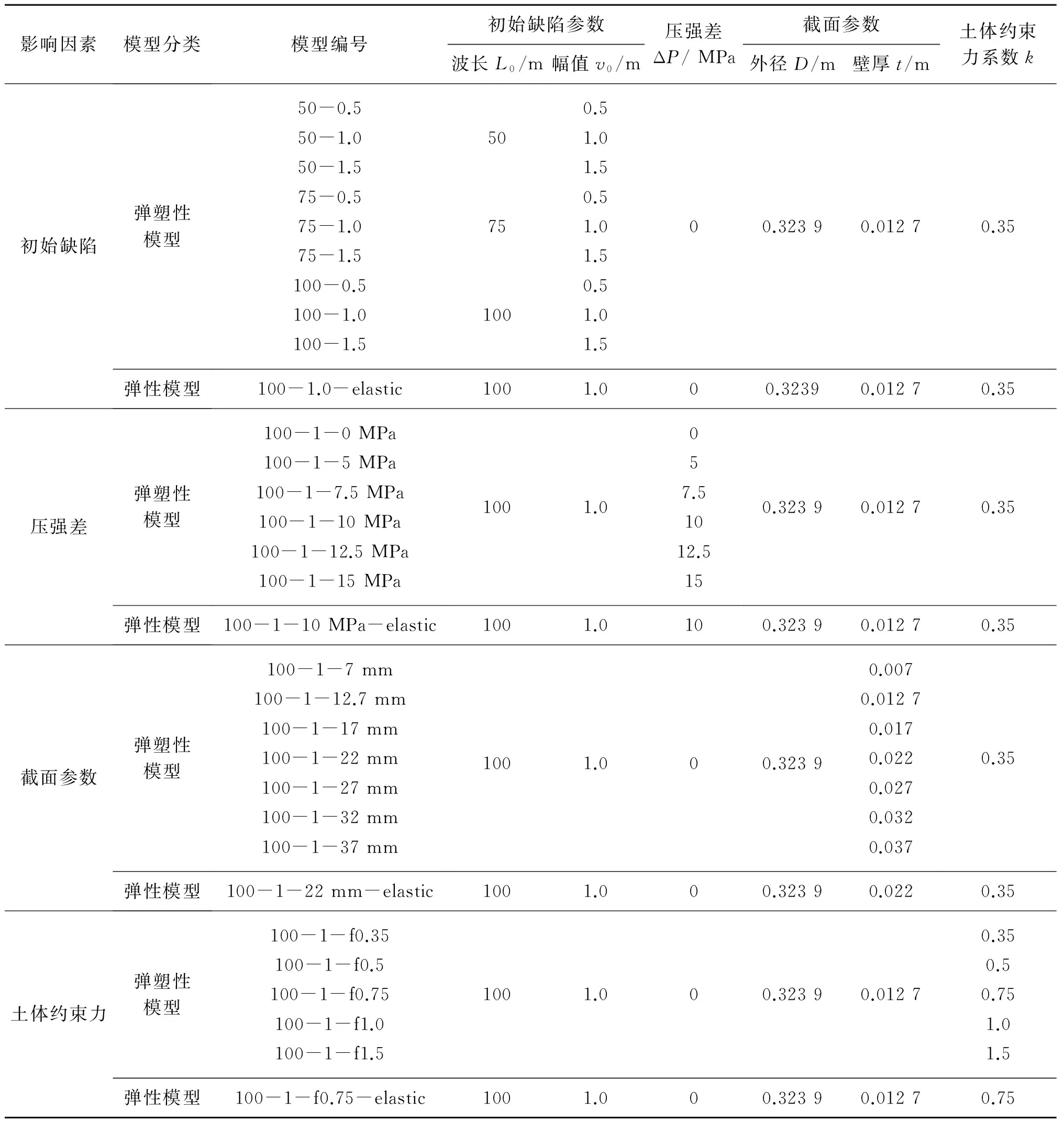
表1 模型参数表Tab.1 Parameters for FEA models
注:管线截面参数的选取参照 API SPEC 5L中关于管线截面的相关规定[15]。
2 数值模拟结果
2.1管线整体屈曲过程中塑性区的分布
海底管线受到温度和压强差的作用以及土体约束力的影响会在管线截面产生压应力,当外荷载较大,截面应力超过屈服强度使得管线进入塑性变形阶段。为研究管线整体屈曲过程中塑性应变的影响,首先需要了解塑性应变产生的时刻、塑性区的分布和变化规律。对上述计算模型进行数值模拟分析后,塑性区的特性统计如表2所示。
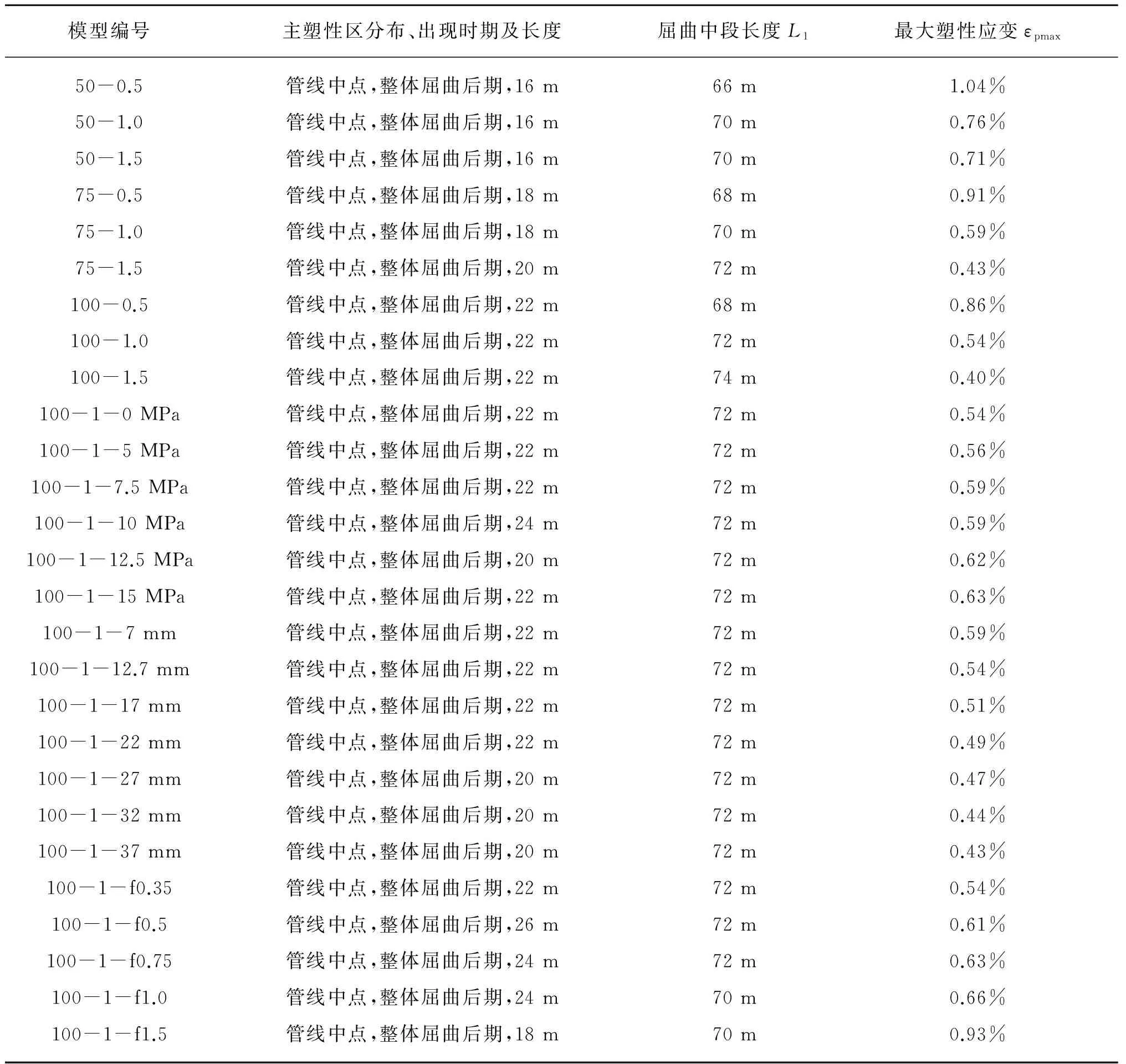
表2 塑形模型结果统计表Tab.2 Results of calculation models
注:屈曲中段长度L1指发生高阶模态整体屈曲的管线中点附近的单拱屈曲段长度,如图3所示。
由表2可知,整体屈曲后的管线塑性应变较小,管线中点附近为主要的塑性区,主塑性区长度都小于屈曲中段长度,主塑性区长度与屈曲中段长度几乎不随影响因素的改变而变化,典型的塑性区分布如图3所示。
由图3(a)可知,整体屈曲后管线的塑性应变主要分布于管线中点附近,即管线水平向变形最大的地方,在原先初始缺陷的两个端点附近也有部分区域产生了塑性应变,但塑性应变值较小。图3(b)显示管线在受到温差为47℃时才开始产生塑性变形,而此时管线已经发生整体屈曲(临界整体屈曲温差约20℃),说明在整体屈曲的临界状态时,管线截面应力尚未达到钢材的屈服强度,管线整体屈曲产生的瞬间水平向变形,来源于屈曲段管线两端的平直段产生指向屈曲段的轴向滑移,而非管线发生较大的塑性变形。同时,由图3(b)中塑性应变的变化可得,塑性应变先出现于管线中点(T=47℃时),即初始缺陷顶点,在整体屈曲后期(T=70℃时)才在原初始缺陷端点附近产生一定的塑性变形,整体屈曲后管线的塑性变形也仅分布于以上3点(1个缺陷顶点和2个端点)附近,在管线的其余部分没有塑性变形。
因此,管线整体屈曲全过程中变形的规律为:先为完全弹性,后出现局部塑形,且塑性区域和塑性应变值较小,主要通过两端管线的轴向伸缩来补偿管线整体屈曲产生的水平向变形。经典解析解中关于管线完全弹性的假设在整体屈曲初期阶段完全适用,在整体屈曲后期与真实情况存在一定的差距。
各计算模型所得的最大塑性应变随影响因素的变化如图4所示。
由图4可知,整体屈曲后管线的最大塑性应变与整体屈曲影响因素有着一定的关联性,最大塑性应变随缺陷幅值、缺陷波长和管线壁厚的增大而减小,随所承受的压强差和土体约束力系数的增大而增大,其中,最大塑性应变与压强差和壁厚呈近似线性关系。
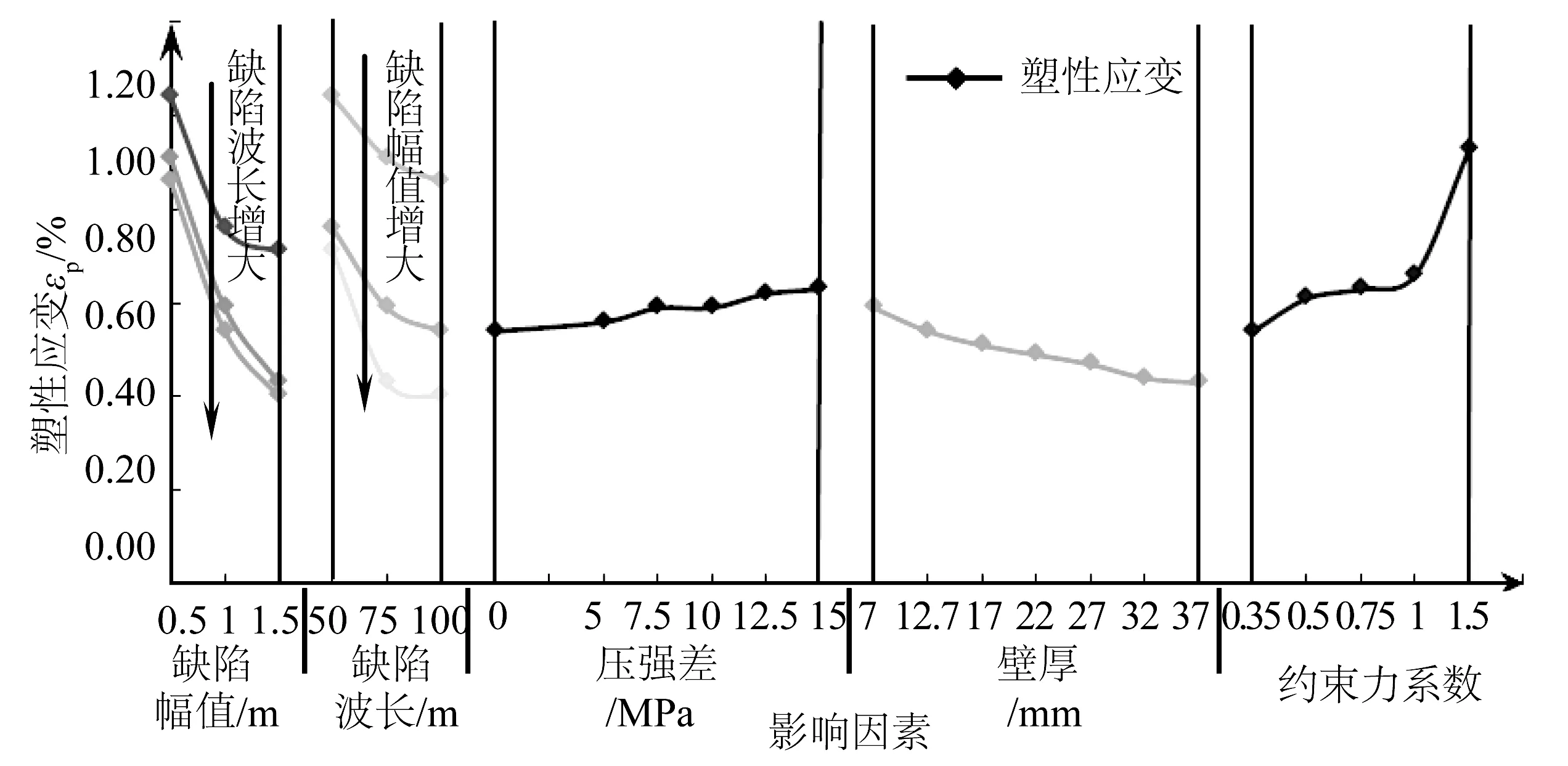
图4 最大塑性应变随影响因素的变化Fig.4 The relationship between the maximum plastic strain and the impact factors
2.2塑性变形对整体屈曲变形的影响
考虑管线钢材塑性后,整体屈曲后管线部分区域出现了塑性变形,对管线的变形形态有所影响。为了解塑性变形对整体屈曲变形形态的影响程度,对部分弹塑性模型设置了相同计算条件下的弹性对比模型。将模型编号为100-1.0、100-1-10 MPa、100-1-22 mm和100-1-f0.75的弹塑性模型与编号为100-1.0-elastic、100-1-10 MPa-elastic、100-1-22 mm-elastic和100-1-f0.75-elastic的弹性模型所得结果进行对比,由于塑性变形出现在整体屈曲后期,因此图5中仅列出整体屈曲变形的最终结果,即T=100℃时的管线变形形态。
由图5可知,由于塑性变形的影响,弹塑性模型部分管段的水平向变形值大于弹性模型相应管段的变形,在塑性变形最为集中、应变值最大的管线中点处,两种模型的差异最大。同时,上述对比结果还显示,在上述4组模型中,没有塑性应变的弹性管段(如图5(a)中的A、B两点处)两种模型的水平向变形也略有差异,说明两种模型水平向变形的差值并非纯粹源于管线产生的塑性变形,管线由于变形协调产生的轴向伸缩量也对两种模型间的差异产生了一定的影响。
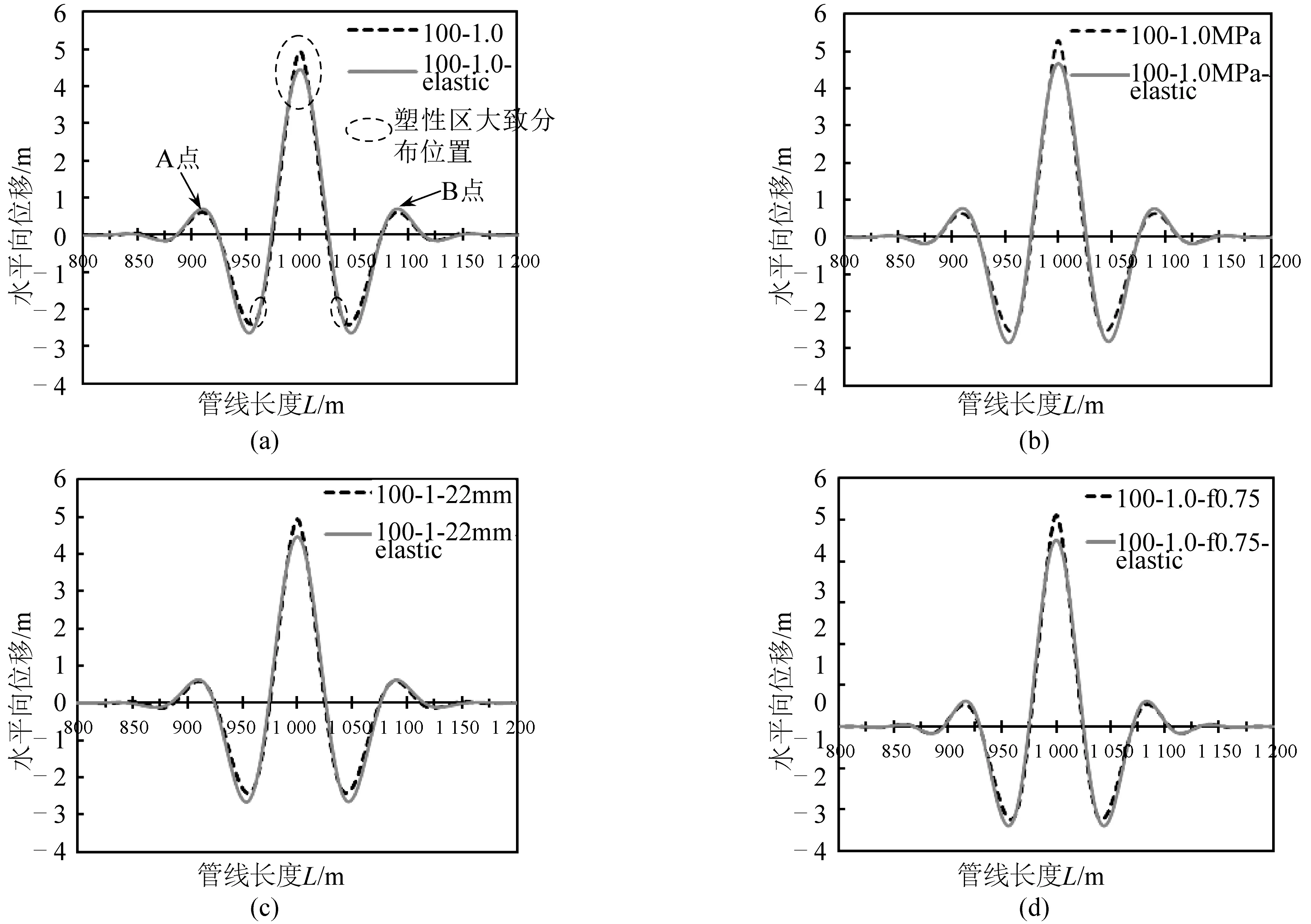
图5 弹塑性模型与弹性模型的最终整体屈曲变形对比Fig.5. The comparison of final lateral deformation between linear FEA and nonlinear FEA
2.3塑性应变造成的截面椭圆化
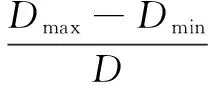
为获得管线整体屈曲引起的管线截面椭圆度,对前述模型在100°C温差,单次升温过程中,发生整体屈曲后截面的椭圆度进行计算,并将结果汇总于表3。
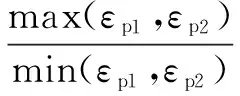
由图6(a)和6(b)可知,椭圆度与最大拉(压)塑性应变值之间的没有较为规则的函数关系,但截面椭圆度与管线最大拉、压塑性应变的比值χ近似呈线性,拟合的函数关系式为f0=0.164 6χ0.170 4,拟合决定系数R2=0.954 5。
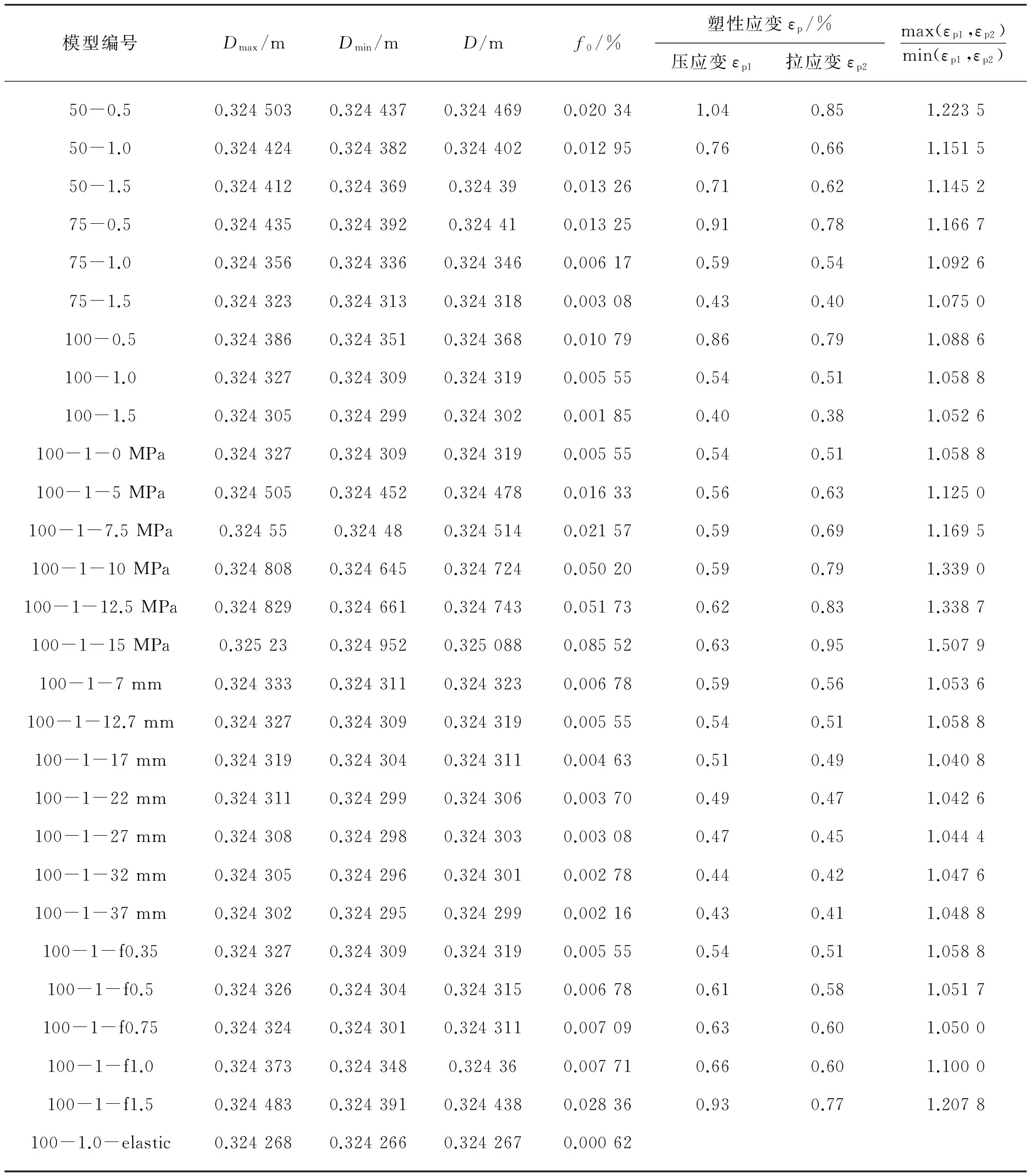
表3 整体屈曲后管线的椭圆度Tab.3 The ovality of post-buckling pipelines
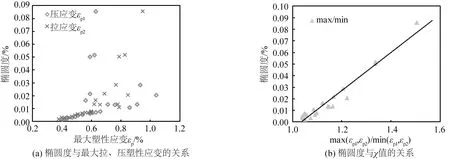
(a) The relationship between ovality and maximum plastic strain (b) The relationship between ovality and χ图6 椭圆度与塑性应变和χ值的关系Fig.6 The relationship between ovality and plastic strain or χ
由于椭圆度随χ值线性增长,获得χ值随影响因素的变化,对判断不同工况下椭圆度的大小有着重要的意义。根据表3可得获得χ值随影响因素的变化关系,如图7所示。
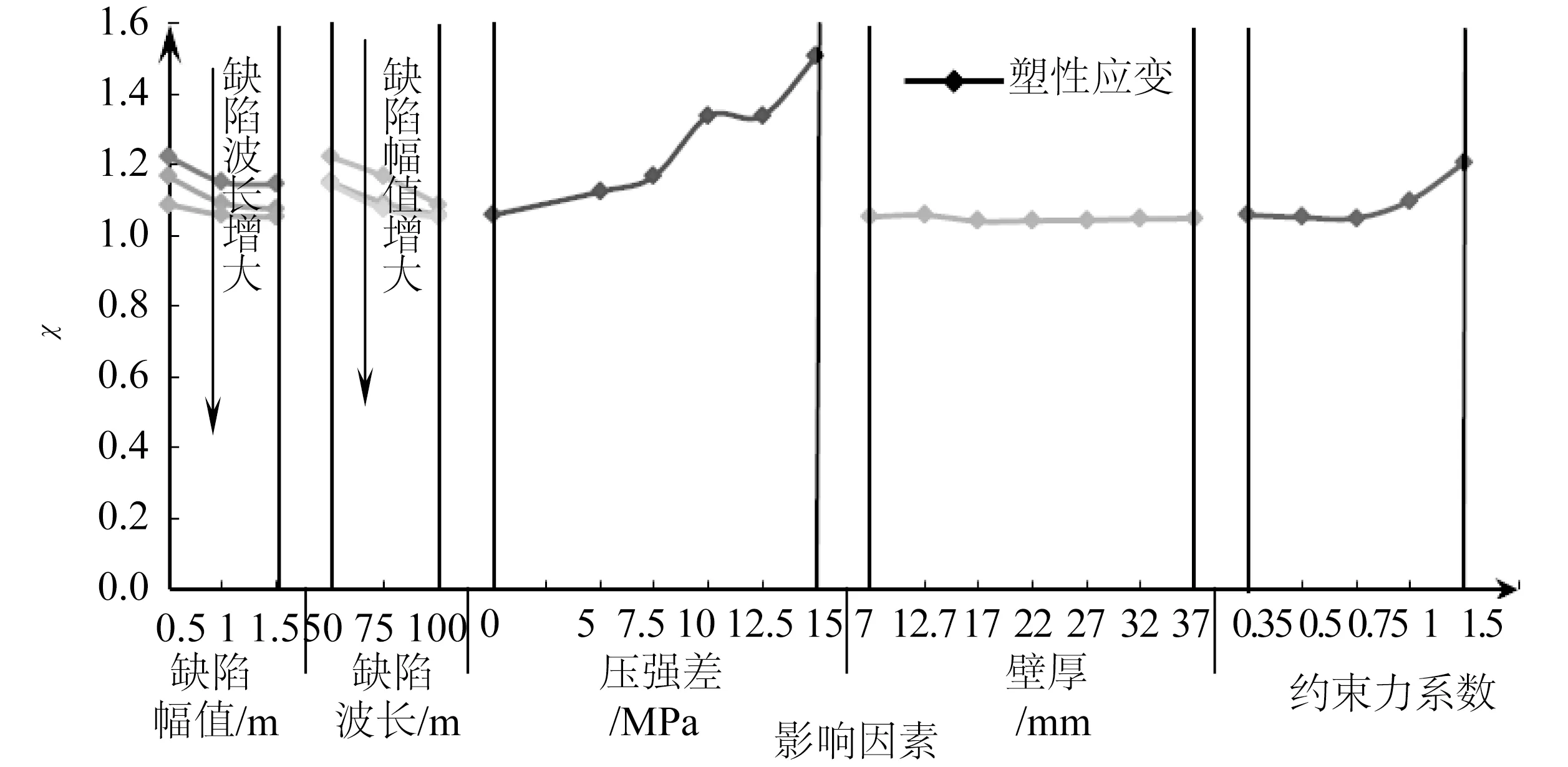
图7 χ值随影响因素的变化关系Fig.7 The influence of impact factors in the value of χ
由图7可知,χ值随壁厚改变的影响不大,随初始缺陷幅值v0 m和波长L0的增大而减小,随压强差Δp的增大而增大,当约束力系数k增加到一定程度后,χ值随约束力系数k的增大而增大。由于椭圆度f0与χ值线性正相关,因此椭圆度f0也随初始缺陷v0 m和波长L0的增大而减小,随压强差Δp和土体约束力系数k的增大而增大。
3 结 语
海底管线发生整体屈曲时,管线部分截面的应力较高,可能会使管线发生塑性变形。本文采用数值分析方法,研究了弹塑性模型下管线整体屈曲过程中塑性区分布及其影响,主要结论如下:
1) 当管线承受温、压荷载发生整体屈曲时,在屈曲过程初期管线维持线弹性状态。随着温度的升高,管线中点处(即初始缺陷顶点处)首先出现塑性变形,而后在原先初始缺陷端点处的管段也进入塑性变形阶段;
2) 整体屈曲中塑性区长度与屈曲段长度相比较小,管线整体屈曲中产生的水平向变形主要还是通过屈曲段两端管线向屈曲段产生滑移而补充相应的变形长度;
3) 管线的塑性应变产生于整体屈曲过程的后期,线弹性模型和弹塑性模型下管线整体屈曲后变形的差异随着管线承受荷载的增大而增大。对承受较低温度的管线,线弹性模型的分析结果仍具有较高的精确度;
4) 整体屈曲后管线的最大塑性压应变与整体屈曲的影响因素有一定的关联性,最大塑性压应变随缺陷幅值、缺陷波长和管线壁厚的增大而减小,随所承受的压强差和土体约束力系数的增大而增大,其中,最大塑性压应变与压强差和壁厚呈近似线性关系;
5) 弹塑性模型模拟管线的整体屈曲时,管线截面会产生较大的椭圆度,椭圆度f0随最大塑性拉、压应变中的较大值与较小值的比值χ线性增加。χ值随壁厚改变的影响不大,随初始缺陷幅值v0 m和波长L0的增大而减小,随压强差Δp的增大而增大,当约束力系数k增加到一定程度后,χ值随约束力系数k的增大而增大。
[1] HOBBS R E.In-service buckling of heated pipelines[J].Journal of Transportation Engineering,1984,110(2):175-189.
[2] TAYLOR N,GAN A B.Submarine pipeline buckling imperfection studies [J].Thin-Walled Structures,1986,4:294-323.
[3] 刘润,闫澍旺,孙国民.温度应力下海底管线屈曲分析方法的改进[J].天津大学学报:自然科学与工程技术版,2005,38(2):124-128.(LIU R,YAN SW,SUN GM.Improvement of the method for marine pipeline upheaval analysis under thermal stress[J].Journal of Tianjin University,2005,38(2):124-128.(in Chinese))
[4] ANTUNES B R,SOLANO R F,VAZ M A.Analytical formulation of distributed buoyancy sections to control lateral buckling of subsea pipelines [C]//Proceedings of the ASME 29th International Conference on Ocean,Offshore and Arctic Engineering.Shanghai,China,2010,5:669-677.
[5] LIU,R,LIU WB,YAN SW.Global lateral buckling analysis of idealized subsea pipelines [J].Journal of Central South University,2014,21(1): 416-427.
[6] HONG ZH,LIU R,LIU WB,et al.Study on lateral buckling characteristics of a submarine pipeline with a single arch symmetric initial imperfection[J].Ocean Engineering(In review).
[7] 洪兆徽,刘润,刘文彬,等.双拱缺陷管线整体屈曲的解析解研究[J].工程力学(In press).(HONG ZH,LIU R,LIU WB,et al.Analytical solution of pipeline global buckling with double arch imperfections[J].Engineering Mechanics,In press.(in Chinese))
[8] VILLARRAGA J A,RODRíGUEZ J F,MARTíNEZ C.Buried pipe modeling with initial imperfections[J].Journal of Pressure Vessel Technology,2004,126(2):250-257.
[9] DE Oliveira Cardoso C,DA Costa A M,SOLANO R F.HP-HT pipeline cyclic behavior considering soil berms effect[C]//25th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers,2006:205-216.
[10] RATHBONE A D,TøRNES K,CUMMING G,et al.Effect of lateral pipe lay imperfections on global buckling design[C]//Proceedings of the 8th International Offshore and Polar Engineering Conference.Vancouver,BC,Canada,2008:224-232.
[11] HONG ZH,LIU R,LIU WB,et al.A lateral global buckling failure envelope for a high temperature and high pressure (HT/HP) submarine pipeline[J].Applied Ocean Research,2015,51:117-128.
[12] CHEE K Y,WALKER A.Assessment of numerical modelling of pipeline lateral buckling [C]// Proc.,Int.Symp.on Lateral Buckling.Australia,2011.
[13] CUMMING G,DRUZYNSKI A,TORNES K,et al.Lateral walking and feed-in of buckled pipelines due to interactions of seabed features[C]//ASME 2009 28th International Conference on Ocean,Offshore and Arctic Engineering.American Society of Mechanical Engineers,2009:739-751.
[14] JUKES P,ELTAHER A,SUN J,et al.Extra high-pressure high-temperature (XHPHT) flowlines:design considerations and challenges[C]//ASME 2009 28th International Conference on Ocean,Offshore and Arctic Engineering.American Society of Mechanical Engineers,2009:469-478.
[15] American Petroleum Institute.Spec A P I.5L,2013[S].Specification for Line Pipe,45th ed.,Washington,DC.
[16] DET NORSKE VERITAS.Offshore standard DNV-OS-F101[S].Submarine Pipeline Systems,2012.
Research on the plastic deformation in the pipeline global buckling process
YAN Shuwang1,HONG Zhaohui1,YAN Yue1,LIU Wenbin2
(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China; 2.CCCC Tianjin Port Engineering Institute Co.,Ltd.,Tianjin 300222,China)
TE58
A
10.16483/j.issn.1005-9865.2016.05.010
1005-9865(2016)05-0083-09
2015-07-30
闫澍旺(1949-),男,天津人,教授,博导,主要从事结构物与土的相互作用研究。E-mail:yanshuwang@tju.edu.cn

