考虑应变率影响的圆管结构冲击试验缩尺修正方法研究

2016-10-12 06:55GeorgeWANG

海洋工程 2016年5期

关键词：缩尺圆管修正

包杰，刘昆，George WANG,3

(1.江苏科技大学船舶与海洋工程学院，江苏镇江 212003；2.上海船舶设计研究院上海 200120；3.美国船级社，新加坡)

考虑应变率影响的圆管结构冲击试验
缩尺修正方法研究

包杰1,2，刘昆1，George WANG1,3

(1.江苏科技大学船舶与海洋工程学院，江苏镇江 212003；2.上海船舶设计研究院上海 200120；3.美国船级社，新加坡)

评估结构耐撞性能最可靠的方法是实尺度碰撞试验，然而对于大尺度结构物的碰撞试验，因其耗资巨大而不易开展，适当开展比例模型试验可以为简化解析算法及数值仿真计算提供验证依据，也可在一定程度上评估结构的耐撞性能。但是在进行碰撞模型试验时，材料应变率的敏感性会使得缩尺模型的动态响应与实尺度结构结果出现偏差，模型试验得到的数据与实际结构的动响应不完全遵循相似关系，这就限制了相似理论在大型结构物冲击问题上的应用。本文给出了一种通过改变冲击质量来修正应变率效应的方法，不同于传统量纲分析法中选取时间、质量和长度为基本量纲，而是以冲击质量、初始冲击速度和动态应力代替，得到计及应变率效应的质量相似关系。以此为基础，将该修正方法应用于船舶-自升式海洋平台的碰撞分析中。研究结果表明，该修正方法可以有效降低由于应变率效应而造成的缩尺误差，修正后的缩尺模型在碰撞冲击载荷下的位移、碰撞力和撞击时间等动态响应参数与实尺度模型结果的一致性更好。本文研究成果可以为大型结构物冲击模型试验设计提供技术支撑。

碰撞试验；应变率敏感性；冲击质量；基本量纲；修正方法

Abstract：It is known that real scale collision tests are the most reliable method to evaluate collision resistance of structures.But it is too expensive for collision tests of large scale structures to be carried out.So the scale model tests are necessary and significant to provide a basis for validating the analytical method and finite element method.It can also reflect the collision resistance of the structure.However,when we carry out impact model tests,the dynamic response will be different between scale model and real scale structure because of strain rate sensitivity.And the model test data and actual dynamic response do not completely follow the similar relationships.So the application of similarity theory in large structures impact problems is limited by the strain rate effect.This paper provides a method to modify the effect of strain rate sensitivity by changing impact mass.The impact mass,initial impact velocity and dynamic stress are selected to obtain the similar relationship instead of the time,mass and length that are the basic dimensions in traditional dimensional analysis.Then,the modified scaled method is applied in the analysis of collision between ships and jack-up platforms.The modified scale method is verified for the problem of the tubular structure of platform subjected to impact loads.The results show that the modified scale method can effectively reduce the errors caused by strain rate effects,and the dynamic response of displacement,impact force and impact time of modified scale model under impact load are in good consistency with prototypes.The research results can provide technical supports for the design of large structures impact tests.

Keywords：collision tests; strain rate sensitivity; impact mass; basic dimensions; modified scale method

碰撞冲击是一种复杂的非线性动态响应过程，国内外学者为了获得结构抗冲击的最佳设计方案进行了许多碰撞方面的研究，也提出了一些分析碰撞问题的方法[1]。其中，评估结构耐撞性能最可靠的方法是实尺度碰撞试验，然而对于大尺度结构物(如船舶、飞机、大楼等)的碰撞试验，因耗资巨大而不易开展[2]，适当开展比例模型的碰撞试验可以为简化解析算法及数值仿真计算提供验证依据，也可以在一定程度上反映分析结构的耐撞性能。众所周知，在进行模型试验时，过大的缩尺比往往使得试验结果与试验预期相差甚远，模型试验得到的数据与原尺度结果不完全遵循相似关系，这是由于完全几何缩尺过程中一些物理现象如应变率敏感性、裂纹的扩展以及惯性现象等[3]无法按照既定相似准则来实现缩尺，且缩尺比越大误差越明显。

随着模型试验的深入开展，国外的学者就缩尺中的不完全相似现象做了一定研究。其中，Booth[4]对低碳钢的薄板进行了1/4缩尺的落锤冲击试验，发现焊缝的断裂和拉长在原尺度结构上更为显著，且由缩尺引起的误差在低碳钢上比在高强钢上更明显。Schleyer[5]等对矩形板进行了不同约束条件的系列缩尺试验，给平板施加了不均匀分布的三角形载荷，发现几何缩尺后平板上出现了不满足相似准则的瞬时响应偏差。Gregory[6]和Me-Bar[7]也做了一系列缩尺方面的研究，指出导致不完全相似的原因首先是应变率敏感性，其次是摩擦表面吸能、材料断裂、热传递等。尽管他们对于结构缩尺过程中出现的不完全相似现象均有了定性的认识，但却没有提供一个可以定量评估或修正这种现象的方法。

本文针对应变率敏感性对缩尺结构碰撞性能的影响进行分析讨论，基于量纲分析法推导得到考虑应变率影响的缩尺修正方法，并选取自升式海洋平台桩腿弦管为典型结构进行有限元计算，验证方法的可靠性。

1 应变率敏感性对缩尺影响

在众多缩尺影响因素中，材料应变率敏感性是造成结构缩尺后不完全相似的主要原因。当结构以相似比λ进行缩尺时，根据相似准则可知模型与材料的应变率存在关系式：

(1)

考虑到本文所用材料是率相关的，利用Cowper-Symonds应变率强化模型，可得表达式：

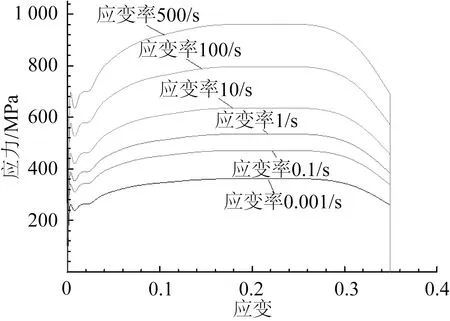
图1 计及应变率敏感性的材料力学性能曲线Fig.1 Material mechanics performance curve considering strain rate sensitivity

≠1

(2)

2 应变率敏感性修正方法

目前国外已经有学者提出缩尺修正方法可以考虑应变率敏感性的影响，使得相似比在一定范围内时缩尺模型可以较好地预测原型的动态响应[3，10]，这些修正方法主要改变初始冲击速度V0或者改变冲击质量G。本文主要通过改变缩尺模型冲击质量进而推导求得冲击质量新的相似关系λG，实现缩尺模型与原型动响应的完全相似。

2.1动态相似准则

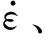
在考虑应变率影响的修正过程中，初始冲击速度和冲击质量是最关键的物理量，因此不同于传统方法中选取时间、质量和长度为基本量纲，本部分将冲击质量、初始冲击速度和动态应力作为基本量纲，建立系统的简化量纲矩阵[10]，如表1所示。

表1 简化量纲矩阵Tab.1 Simplified dimensional matrix

通过量纲间的矩阵换算得到无量纲π数，即碰撞动态相似准则，如式(3)所示：

(3)

2.2碰撞物理量相似比

不同于传统方法中各物理量的相似比都由几何缩尺比来表征，此修正方法中每个物理量的相似比都使用自己的变量来表示[10]，如冲击质量的相似比λG和初始冲击速度相似比λV0。定义动态应力的相似比为：

(4)

由无量纲数π3得：

(5)

这里是对冲击质量进行修正，缩尺过程中保持初始冲击速度不变，故λV0=1，可得：

λG=λ3λσd

(6)

由无量纲数π4得：

(7)

将式(5)带入式(6)中，可得：

(8)

由式(4)、式(6)、式(8)可得：

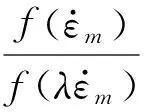
(9)

式(9)是质量修正方法中的关键公式，反应了考虑应变率影响下修正缩尺模型冲击质量与原尺度模型之间的相似关系。通过式(9)可以得到计及应变率效应的缩尺模型冲击质量。

2.3修正的一般步骤

1)确定缩尺模型的相似比λ。

2)求出模型内部的应变率。

3)获得动态应力相似比λσd。

4)运用式(9)计算λG得到修正后的冲击质量。

3 受横向冲击载荷圆管内部应变率的求法

由于自升式海洋平台桩腿为管节点的组合结构，故选取受横向冲击载荷圆管为本部分的研究对象，如图2所示，其中圆管长2L，内外半径分别为r、R，两端刚固，冲击物定义为刚体，质量G，撞击速度V，撞击的位置位于圆管跨中。通过推导求解受横向冲击载荷圆管内部的应变率，探究应变率敏感性对此种结构缩尺的影响，从而为船舶-自升式海洋平台碰撞模型试验的缩尺方案提供基础和依据。

图2 两端刚固圆管受横向冲击载荷Fig.2 Circular tube fixed on both ends under lateral impact load

3.1等效应变

基于米塞斯屈服准则，两端刚固的梁受到动态集中载荷时，结构等效应变定义为[11]：

(10)

由于梁沿x轴方向，冲击速度沿z方向，故εyy=εzz=0.3εxx，γxy=γyz=0，其中0.3为泊松比，得：

(11)

可见圆管结构等效应变由两部分组成，即弯曲应变εxy和剪切应变γxz，下面阐述两种不同应变的求法。

3.2弯曲应变

由文献[11]可知，圆管在冲击载荷作用点处的弯曲应变公式为：

(12)

式中：W为冲击载荷作用点处的位移。

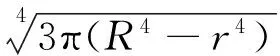
代入式(12)，得：

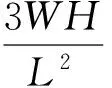
(13)

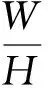
εxx=εM=3h2w

(14)

式(14)就是受横向集中载荷圆管碰撞区域的弯曲应变表达式。

3.3剪切应变

由文献[11]可知圆管的剪切应变沿长度方向可视为定值，约为：

γxz=Ws/(lQ/a)

(15)

式中：Ws为梁的剪切位移；lQ为梁的剪切铰区长度，即由于剪切而引起的弹塑性梁上非弹性变形集中区域的长度[11]。对于两端刚性固定的梁，其剪切铰区长度为lQ=0.551H≈1/2H；系数a是基于试验结果[12-13]取得，这里取a=2。

根据文献[14]中试验和数值回归的结果，可得：

Wsf=kHWs/L

(16)

根据文献[15]中的数值研究可以假定

(17)

最后由式(15)、式(16)、式(17)可得：

γxz=4khw

(18)

式(18)就是受横向载荷圆管的剪切应变表达式。

3.4等效应变率

由式(11)、式(14)和式(18)可得两端刚固受动态集中载荷梁等效应变的表达式：

(19)

(20)

(21)

将式(21)中圆管内部应变率带入式(9)可得圆管侧向冲击修正后的冲击质量相似比：

(22)

4 修正方法的有限元验证

4.1有限元模型

图3 简化有限元碰撞模型Fig.3 Simplified finite element model of collision

将第三节中应变率的求解方法运用于船舶-自升式海洋平台的碰撞问题中，需要对其进行一定的简化。由于第三节中定义撞击物为刚体，且本文的研究重点是探讨应变率敏感性对被撞结构缩尺的影响，故将撞击船球鼻艏简化为刚性半球，质量3 000 t，撞击动能6 000 kJ，被撞平台桩腿简化为撞击区域的弦管结构，如图3所示。

运用有限元软件ABAQUS进行建模计算，弦管结构材料选用低碳钢，其基本力学性能见表2。为了在软件输入中反映出材料的率相关，材料本构选用Cowper-Symonds应变率强化模型，其不同应变率下材料的应力-应变关系如图1所示。

表2 平台用低碳钢的基本力学特性Tab.2 Basic mechanical properties of mild steel

弦管侧向撞击过程选用动态显性分析步(Dynamic Explict)，选用通用接触，同时，对弦管两端刚性约束，撞击船运动方向位于管节点平面，垂直于弦管方向，初速度为2 m/s。

为了验证修正方法的可靠性，需要建立不同缩尺比的碰撞模型。参考大变形动态相似准则[18,19]，碰撞各物理相似关系详见表3，根据相似比尺建立不同缩尺比下的简化碰撞模型，模型具体尺寸参数如表4所示。

表3 碰撞各物理量相似比尺Tab.3 Similar scale of various physical quantities during the collision

表4 原型与缩尺模型尺寸参数表Tab.4 Prototype and scale model size parameter table

本文研究的重点在于修正应变率敏感性对结构缩尺的影响，而2 m/s的冲击速度下结构材料的应变率较小，其对缩尺的影响不明显，为了更加直观地反映考虑应变率影响的缩尺修正方法的效果，同时排除其它影响因素，故在保持总的冲击动能不变的前提下，增大冲击速度的同时减小冲击质量，分别选取三组不同初始冲击速度10、15和20 m/s(即不同应变率)进行分析验证。结合式(9)和式(22)求得各工况下质量修正系数，并反映到修正的有限元模型中，修正中所需的主要参数见表5，修正前后的各工况碰撞参数见表6。

表5 修正所需主要参数Tab.5 Main parameters in correction

表6 修正前后主要参数汇总表Tab.6 Summary table of main parameters before and after modification

4.2计算结果与分析

将不同缩尺比的弦管碰撞模型提交计算，可以获得撞击过程接触力的合力(碰撞力)及撞击船位移随时间变化的曲线。为了便于更加直观地比较缩尺前后物理量的关系，将缩尺模型时历曲线中各横坐标t按时间比尺放大，同时也将纵坐标按各自的缩尺比放大即得相似等效后的时历曲线图。

图4 速度20 m/s位移时历曲线Fig.4 The displacement-time curves of velocity 20 m/s

图5 速度20 m/s碰撞力时历曲线Fig.5 The collision force-time curves of velocity 20 m/s

图4和图5给出了初始冲击速度为20 m/s时原型与缩尺比为10的模型修正前后等效位移和碰撞力时历曲线。曲线的走势可以反映撞击过程，其中位移曲线先增后减，可知撞击船在与弦管结构相互作用的过程中先正向减速至零，后由于被撞结构的弹性被反向弹开，曲线峰值对应撞击船的极限撞深；碰撞力曲线则经历了振荡、平稳和衰减三个阶段，表现在结构上为碰撞初期弦管由于自身弹性处于振荡阶段，随着撞深的增加变形超越弹性进入塑性流动，此阶段碰撞力较为平稳，直至达到极限撞深后碰撞力开始卸载，曲线逐渐衰减为零。但未修正缩尺模型的曲线与原型仍存在较大差异，其中极限撞深较原型有明显减小，碰撞力峰值较原型偏大，碰撞持续时间偏短。通过查看相似理论可知模型缩尺使得应变率增大，从而带动材料的应力应变关系发生变化，由图1可知材料的强度随应变率的增大而增大，故使得撞深减小，碰撞力增大。修正后缩尺模型的曲线与原型吻合度很好，峰值处的偏差也大大减小，其中位移峰值偏差由9.68%减小到1.85%，碰撞力峰值偏差由22.12%减小到2.81%，同时碰撞持续的时间也与原型更加接近。因此修正后的模型表现出与原型更好的相似度。

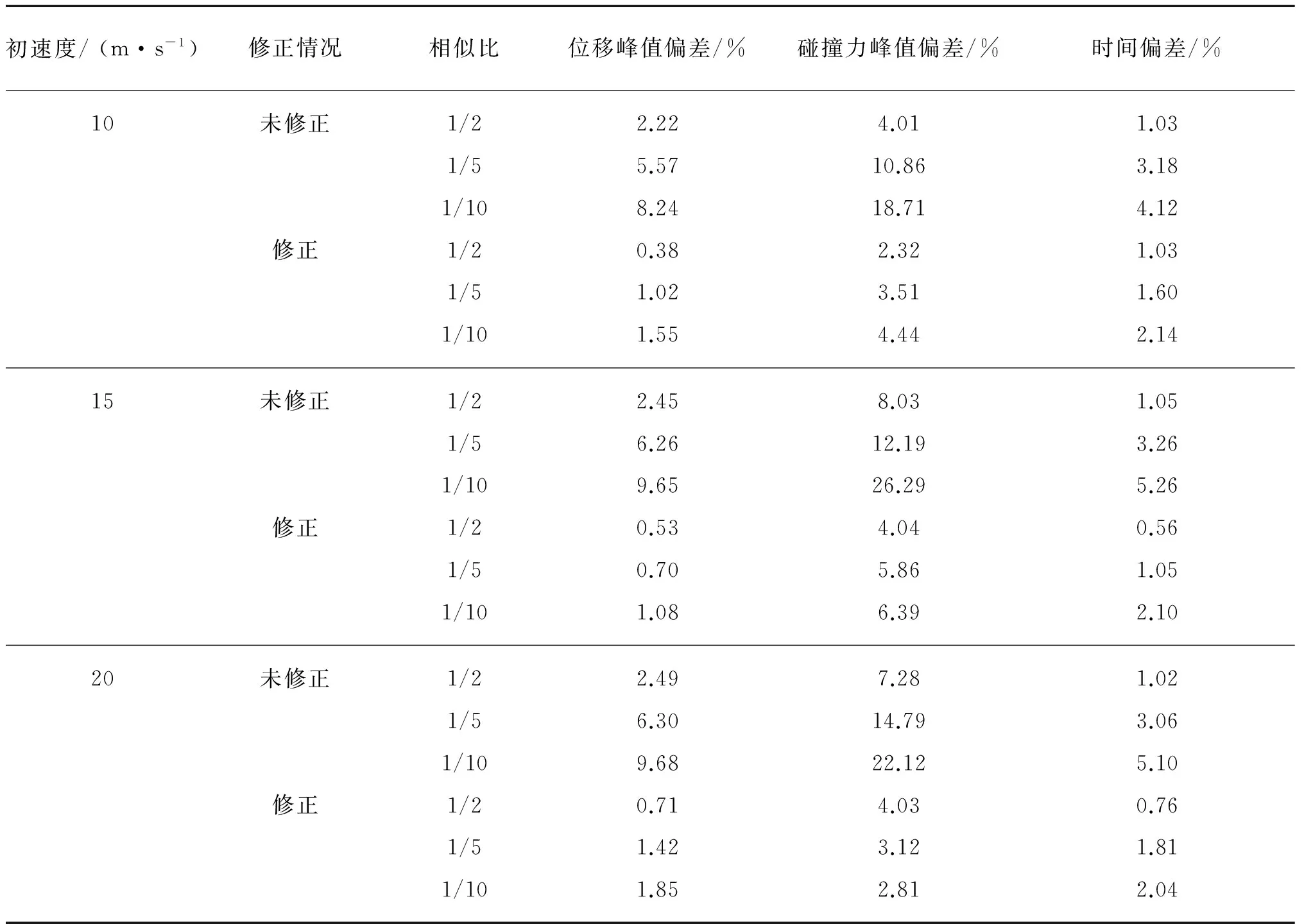
表7 修正前后误差分析汇总表Tab.7 Summary table of error analysis before and after modification

表7给出了三种速度对应三种缩尺比下模型修正前后的误差分析汇总表。从表中可以看出，通过应变率的修正均可以将误差成倍减小，如速度20 m/s缩尺比10的模型碰撞力的偏差值减小到原来的1/8，可见修正方法在此种结构碰撞问题中具有较高的可靠性，并可适用于船舶-自升式海洋平台模型试验中。

5 结语

基于应变率敏感性对缩尺的影响，给出了碰撞类冲击问题结构缩尺修正的方法，并以受横向冲击载荷圆管的缩尺为例，验证了修正方法的可靠性。主要结论如下：

1)以冲击质量、初始冲击速度和动态应力为基本量纲，运用量纲分析法可以得到考虑应变率敏感性的各物理量相似比，从而得到相应的修正方法，使得碰撞类冲击问题的缩尺修正成为可能。

2)以船舶-自升式海洋平台碰撞为背景，将考虑应变率敏感性的缩尺修正方法应用到平台桩腿弦管冲击问题当中，通过理论推导与数值计算，大大减小了极限撞深、碰撞力和撞击时间在缩尺过程中造成的误差，验证了该修正方法的可靠性，为大型海洋结构物冲击问题的缩尺试验方案设计提供了基础。

[1] OSHIEO R E,ALVES M.Predicting the behavior of structures under impact loads using geometrically distorted scaled models[J].Journal of the Mechanics and Physics of Solids,2012,(60)：1 330-1 349.

[2] 温小飞，卢金树，崔振东.船舶碰撞过程的数值模拟及试验研究[J].浙江海洋学院学报(自然科学版),2011,30(01)：71-76.(WEN X F,LU J S,CUI Z D.Numerical simulation and experiment research of ship collision process[J].Journal of Zhejiang Ocean University (National Science),2011,30(01)：71-76.(in Chinese))

[3] OSHIEO R E,ALVES M.Scaling of cylindrical shells under axial impact[J].International Journal of Impact Engineering,2007,(34)：89-103.

[4] BOOTH E,COLLIER D,Miles J.Impact scalability of plated steel structures[J].Structural Crashworthiness,London,1983：136-174.

[5] SCHLEYER G K,HSU S S,WHITE M D.Scaling of pulse loaded mild steel plates with different edge restraint[J].International Journal of Impact Engineering,2004,46(9)：1267-1287.

[6] GREGORY L F.Replica model scaling for high strain-rate events[J].International Journal of Impact Engineering,1995,16(4)：571-583.

[7] ME B Y.A method for scaling ballistic penetration phenomena[J].International Journal of Impact Engineering,1997,19(9-10)：821-829.

[8] 王自力,顾永宁.应变率敏感性对船体结构碰撞性能的影响[J].上海交通大学学报,2000,34(12)：1 704-1 707.(WANG Z L,GU Y N.Effect of strain-rate sensitivity on the behavior of ship structure in collision[J].Journal of Shanghai Jiaotong University,2000,34(12)：1 704-1 707.(in Chinese))

[9] 王自力,蒋志勇,顾永宁.船舶碰撞数值仿真的附加质量模型[J].爆炸与冲击,2002,22(4)：321-326.(WANG Z L,JIANG Z Y,GU Y N.An added water mass model for numerical simulation of ship/ship collisions[J].Explosion and Shock Waves,2002,22(4)：321-326.(in Chinese))

[10] ALVES M,OSHIEO R E.Scaling the impact of a mass on a structure[J].International Journal of Impact Engineering,2006,32(7)：1 158-1 173.

[11] ALVES M,JONES N.Impact failure of beams using damage mechanics：Part I[J].International Journal of Impact Engineering,2002,27(8)：837-861.

[12] WEN H M,REDDY T Y,REID S R.Deformation and failure of clamped beams under low speed impact loading[J].International Journal of Impact Engineering,1995,16(3)：435-454.

[13] JONES N,KIM S B,LI Q M.Response and failure of ductile circular plates struck by a mass[J].ASME Journal of Pressure Vessel Technology,1997,(119)：332-342.

[14] ALVES M,JONES N.Impact failure of beams using damage mechanics：Part I[J].International Journal of Impact Engineering,2002,27(8)：863-890.

[15] YU J L,JONES N.Numerical simulation of a clamped beam under impact loading[J].Compute Structure,1989,32(2)：281-293.

[16] PERRONE N,BHADRA P.A simplified method to account for plastic rate sensitivity with large deformations[J].Journal of Applicant Mechanics,1979,(46)：811-816.

[17] LIU K,Wang Z L.Experimental and numerical simulation of laterally impacted stiffened plates considering the effect of strain rate[J].Ocean Engineering,2015,(99)：44-54.

[18] 雷正保.汽车结构的大变形动态相似准则及相似计算精度[J].实验力学,2000,15(4)：429-435.(LEI Z B.Dynamic similarity criteria for automotive structures of elastic-plastic materials under large deformation condition and precision of similarity calculation[J].Journal of Experimental Mechanics,2000,15(4)：429-435.(in Chinese))

[19] 雷正保.大位移大转角弹塑性相似结构的相似比[J].机械工程学报,1999,35(2)：6-9.(LEI Z B.Similitude ratios of elastic-plastic similitude structure with large displacements and large deformations for dynamic system[J].Chinese Journal of Mechanics Engineering,1999,35(2)：6-9.(in Chinese))

Research on the modified scale method for impact tests of tubular structuresconsidering the effect of strain rate

BAO Jie1,2,LIU Kun1,George WANG1,3

(1.School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China；2.Shanghai Merchant Ship Design and Research Institute,Shanghai 200120,China；3.American Bureau of Shipping,Singapore)

P751

10.16483/j.issn.1005-9865.2016.05.009

刘昆。E-mail：justkliu@hotmail.com

1005-9865(2016)05-0073-10

2015-09-23

国家自然科学基金资助项目(51379093)；江苏省高校自然科学基金资助项目(15KJD580003)