三维自由面流动模拟中GPU并行计算技术
李海州,唐振远,万德成
(1.上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240;2.高新船舶与深海开发装备协同创新中心,上海 200240)
三维自由面流动模拟中GPU并行计算技术
李海州1,2,唐振远1,2,万德成1,2
(1.上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240;2.高新船舶与深海开发装备协同创新中心,上海 200240)
MPS(Moving Particle Semi-implicit)法能够有效地处理溃坝、晃荡等自由面大变形流动问题。在三维MPS方法中,粒子数量的急剧增加会导致其计算效率的降低并限制其在大规模流动问题中的应用。基于自主开发的MPS求解器MLParticle-SJTU,本文对求解过程中耗时最多的邻居粒子搜寻和泊松方程求解两个模块采用了GPU并行加速,详细探讨了CPU+GPU策略。以三维晃荡和三维溃坝这两种典型的自由面大变形流动为例,比较了CPU+GPU相对于MLParticle-SJTU串行求解时的加速情况,结果表明CPU+GPU在邻居粒子和泊松方程这两个模块中的加速比最高能达到十倍左右。此外,采用CPU+GPU并行能够较准确地模拟溃坝、晃荡等自由面大变形问题。
MLParticle-SJTU求解器;邻居粒子搜索;GPU并行技术;稀疏矩阵求解;溃坝;晃荡
Abstract:MPS (Moving Particle Semi-implicit) is very suitable to deal with free surfaces flows of large deformation such as dam-breaking and sloshing flows.However,the computational efficiency of the MPS method becomes a bottle neck for large-scale engineering applications with the increase of the number of particles,especially for 3D flow problems.Based on our in-house solver MLParticle-SJTU,the present work applies GPU technique in searching for neighboring particles and solving pressure Poisson equation,which are two most time-consuming parts in the MPS.The acceleration performance is analyzed according to 3D sloshing and 3D dam breaking flows.The results show that a speedup up to 10x can be achieved by CPU+GPU acceleration compared to that by only one CPU.
Keywords:MLParticle-SJTU solver; neighbor list search; GPU parallel computation; sparse linear equation; sloshing;dam-breaking wave
无网格粒子法MPS(Moving Particle Semi-implicit)[1-3]能够有效地处理自由面大变形流动问题,如晃荡、溃坝等。尽管如此,当该方法应用到三维流动问题时,粒子数和计算量会急剧的增加,基于传统的CPU串行计算已经很难满足工程应用的需要。因此,如何有效地提高MPS方法在三维问题中的计算效率就显得尤为重要。
近些年来,已有学者在尝试着通过多CPU并行计算来提高MPS方法的计算效率。Ikari 和 Gotoh[4]分析了粒子分解法和区域分解法两种并行策略的优缺点,结果显示区域分解法能够获得较好的并行效率;Gotoh 等[5]开发了一个三维 MPS 并行求解器,采用MPI实现进程间通信,研究了三维破波问题,并分析了不同迭代方法的并行效率。Iribe等[6]介绍了一种基于粒子分解法的并行 MPS 方法,为了减少因粒子分解带来的进程间通信量,作者采取了优化措施,如对粒子重新编号、提前生成缓冲区粒子列表,这些做法提高了并行效率,最后计算了波浪在海岸的演化问题。张雨新等[7]基于MPI并行库和动态负载平衡技术开发了粒子法并行求解器MLParticle-SJTU,数值测试表明该求解器能够获得较好的加速比。上述研究表明CPU并行确实能够有效地提高计算效率。一般地,随着核数的增加,计算效率有增大的趋势。因此,如果能够有效利用足够多核数进行并行计算的话,可能会得到非常可观的计算效率。
另外,一种拥有非常多核数的处理器引起了大家的注意,即GPU(图形处理器)。为了处理大规模的图像数据,GPU在硬件结构、指令流程和浮点数计算能力等方面做了大量的优化。同时,GPU的计算核心数也远远高于CPU,比如一块消费级显卡就拥有数百乃至上千个计算核心。而以上这些特性也奠定了GPU拥有强大并行计算能力的基础。因此,现在也有不少人开始考虑如何充分利用GPU的并行能力。
在粒子法领域,关于GPU并行的工作最早见诸于一种提出较早的无网格粒子法SPH(Smoothed Particle Hydrodynamics)中。Harada等[8]以及Zhang等[9]最早将GPU技术应用到无网格粒子法SPH。随后GPU在SPH上的应用逐渐增多。Crespo等[10]对SPH理论及某些关键问题的不同处理方式进行了综述,并比较了SPH方法在CPU和GPU上实现的异同。计算结果表明,在使用单块GPU进行百万级别粒子数的模拟时,较单核CPU能获得两个数量级的加速比。Dominguez等[11]研究了CPU-GPU计算平台的优化问题。对于CPU端,提出了将计算域划分为更小的Cell单元以及利用OpenMP等优化措施。对于GPU端,则提出了最大化并行率、减少全局内存访问等优化策略。相较于SPH而言,GPU在MPS中的应用就相对较少。其中,Hori 等[12]采用 CUDA (Compute Unified Device Architecture) 库开发了基于 GPU加速的二维MPS并行程序,获得了数倍到十多倍的加速比;朱小松[13]针对晃荡问题研究了MPS的GPU并行计算及其优化分析。这些应用大多是集中在二维问题上,三维应用所开展的工作还比较少。
本文的主要目标是基于课题组自主研发的CPU并行求解器MLParticle-SJTU[14-20],研究如何利用GPU并行技术来提高三维MPS的计算效率。其中,求解器MLParticle-SJTU是基于改进的MPS方法,利用C++语言和MPI并行库自主开发的,目前该求解器已经应用到液舱晃荡[15-18]、溃坝[19,20]等问题。针对MPS方法中最耗时的求解部分:邻居粒子搜寻和泊松方程求解,本文详细地讨论了GPU并行技术分别在这两部分中的加速策略。由于CPU上的算法并不能直接应用到GPU上,本文采用对原有CPU计算程序的部分模块进行GPU化的方法来研究GPU并行技术在三维MPS中的应用。为了与CPU并行以及全GPU并行相区别,本文将MPS中部分模块GPU化的方法称之为CPU+GPU并行。最后,本文将通过对三维晃荡问题和三维溃坝问题的仿真模拟来验证CPU+GPU并行在三维MPS方法中的可行性和有效性。
1 CPU+GPU并行模型
1.1GPU计算架构
GPU(Graphics Processing Unit),即图形处理器,最初主要用于图形处理的加速,随着技术的不断革新,目前GPU已发展成为一种高度并行化、多线程、多核的处理器,具有非常大的计算吞吐量和相当高的存储器带宽。如图1[21]所示,GPU相较于CPU划分了更多的执行单元(ALU),即更多的计算核心,从而能并发执行相当多数量的线程,而这也正是GPU拥有强大并行计算能力的原因所在,也即GPU是专为计算密集型、高度并行化的计算而设计。
1.2CPU+GPU执行方式
从上节可以看到,GPU的硬件结构决定了GPU可以进行高效率的并行计算。但是,要充分利用其并行性能,则需要一个简单、有效的操作平台,本文的CPU+GPU工作是基于NVIDIA公司推出的软件加硬件操作平台CUDA(Compute Unified Device Architecture,通用并行计算架构)来进行开发的。在CUDA模型中,CPU被称为主机(Host),而GPU被称为设备端(Device)。一个典型的CPU+GPU混合计算的工作流程如图2所示。在执行任务时,先由主机端程序开辟任务所需的内存或显存,然后将主机端数据拷入显存中,设备端接收到主机端的执行指令后执行相应的任务要求,执行结束后,将执行结果传递给主机端,主机端释放开辟的内存或显存,执行结束。
在主机端,程序的执行和只有CPU情况下的运行模式是一样的,可串行可并行。本文的计算中,主机端的程序都是串行进行的。

图1 GPU与CPU相比分配了更多的晶体管用于数据处理[21]Fig.1 The GPU devotes more transistors to data processing[21]

图2 CPU+GPU执行模式Fig.2 The execution mode of CPU+GPU
在设备端,程序是以线程为基本单位来运行的。而线程间则是以Thread、Block、Grid的三维组织层次来执行的。其中,每个Block由若干个Thread组成一维、二维、三维的形式,而Block则以一维、二维、三维的形式组成Grid。在计算时,计算任务将分配到相应的流多处理器(Stream Multiprocessors,SM)中,而流多处理器又将任务分配到Grid中,如此向下传递,最终到达Tread执行任务。任务完成后,则将计算结果返回,最终回到主机端。
总的来说,CPU+GPU的运行模式就是由CPU端提供GPU端计算所需要的初始数据,而当GPU端计算完成之后,就将结果传输回CPU端,从而构成一次CPU+GPU计算。
2 MPS的CPU+GPU并行方案
2.1MPS串行时间开销分析
本文分析MPS计算程序MLParticle-SJTU串行时各模块的CPU时间开销,并找出耗时最大的模块。求解器采用了改进的MPS方法[14-20],该方法将原始MPS方法中需要的两次邻居粒子搜寻降低到了一次,这在一定程度上优化了MPS的计算效率。图3(a)是原始的MPS计算流程,图3(b)给出了改进的MPS计算流程。
本文在linux平台下选取了一个三维溃坝(溃坝尺寸与后文中的溃坝算例相同)作为时间开销分析的测试算例,统计了100个时间步长的计算时间,并分析各部分的时间比例。统计结果如表1所示。

表1 MPS各部分时间占比情况Tab.1 The distribution of running time of MPS
从表1可以看到,PartB和PartD所占的时间比例最大,其余部分则几乎可以忽略。其中,PartD所占用时间比例高达82.74%,而其对应的部分为泊松方程求解模块。PartB对应占比11.33%则位居第二,并远远高于剩下的部分。其中邻居粒子搜寻是整个PartB的核心,其耗时占PartB的50%左右(表中没有列出)。从上述分析结果可以看到,在三维MPS计算中,邻居粒子搜寻和泊松方程的求解是制约计算效率的关键因素。因此,本文研究CPU+GPU并行加速在PartB和泊松方程求解中的加速策略。

图3 MPS计算流程Fig.3 The flow chart of MPS
2.2PartB的并行化方案
2.2.1 粒子搜寻的基本思路
PartB包含了建立邻居粒子对的三个步骤:邻居粒子搜寻、核函数计算、更新粒子对信息。其中核函数计算和更新粒子对信息实现起来比较容易,且步骤单一,所以不需要特别讨论。而PartB中的邻居粒子搜寻则是一个相对较复杂的问题,本文将对该问题进行详细讨论。
目前,普遍采用的粒子搜寻方法有CLL(cell-linked list)和VL(Verlet list)两种[ 23],其基本思想都是将粒子搜索域划分成一个个很小的单元,从而缩小搜索范围,提高搜索效率。由于原始的CPU程序采用的是CLL方法,也就是要构建链表保存所有的邻居粒子对,因此,本文的GPU端也要采用与之相适应的搜寻方法。

图4 邻居粒子搜寻范围Fig.4 The schematic diagram of neighbour searching
邻居粒子搜寻共分为两部分,首先要把所有粒子分配到背景单元中,这个可以通过对某一指定坐标点来计算所有粒子的相对坐标来实现;其次,利用分配好的背景单元来搜寻邻居粒子,以三维情况为例,每个粒子的搜寻范围应该如图4所示。可以看到,每个粒子只搜寻了一半的范围(单独来看的话,三维问题应该是上中下共三层27个单元都是潜在邻居粒子单元),这是因为在GPU上每个粒子的邻居粒子搜索操作均由一个对应的线程来完成,因此如果每个粒子都搜寻所有的邻居粒子,那么将会导致最后的邻居粒子列表重复。因为邻居粒子对是成对出现的,i粒子是j粒子的邻居粒子,那么j也是i的邻居粒子,所以如果都进行完全搜寻的话,将会造成邻居粒子对重复。
在对这一过程进行并行化的时候,还有一个值得注意的问题就是邻居粒子对的存储问题。图5给出了串行和并行程序中,邻居粒子对的存储情况。串行时需要预先估算一个最大的邻居粒子数来分配粒子对的存储空间。在并行处理时,由于每个线程都要进行粒子搜寻,所以要为每一个线程都分配存储空间,这就要求对每个线程估算一个最大的粒子数上限。而这个最大粒子数上限则和具体问题以及计算粒子数等相关,为了保险起见,该最大粒子数必须预留足够的空间,因此需要取足够大的值,这无疑会增加内存的消耗量。此外,由于在GPU端完成粒子搜寻后需要将数据传回CPU端,之前分配过大的数据存储空间则会造成数据传输时间增大,这也将一定程度上制约GPU的加速效果。
2.2.2 粒子搜寻中的优化措施
1) 合并保存两种作用域的邻居粒子。在MPS方法中,存在着两种粒子作用域的离散:一种是散度和梯度的离散,其作用域取为2.1倍的初始粒子间距;另一种则是拉普拉斯算子的离散,其作用域取为4.0倍的初始粒子间距[1]。由于第一种作用域内的邻居粒子必定属于第二种邻居粒子,因此只需要考虑拉普拉斯算子作用域情况下邻居粒子的情况来分配存储空间。
2) 数据传输优化。在GPU完成计算后需要把数据传回CPU端。当传输的数据量很大时,有限的传输速度就成为了瓶颈。在CUDA存储模型中,提供了一种称为锁页内存的模式,使用该内存后将在CPU内存中分配出专门用于与GPU存储进行数据传输而不参与其它CPU任务的空间,并允许GPU进行DMA(直接内存访问)。因此,使用锁页内存能够有效提高数据传输。
3)提取邻居粒子对的优化。如图5所示,CPU+GPU并行计算后的数据分布与串行的数据分布是不一样的。因此,需要将GPU并行计算得到的结果重新拼接为串行时的情况,也即拼接所有邻居粒子为一个连续的内存。在这个过程中,对于并行产生的零散结果进行拼接时,尽量使用整段内存copy拼接要比遍历插入效率高很多。

图5 串行与并行中粒子对存储情况Fig.5 The storage of particle pairs in serial and parallel compatations
2.3泊松方程求解的并行化方案
在MPS方法中,流体是不可压的,其压力是通过对压力泊松方程的求解得到的。本文所采用的改进的MPS方法[22]中,压力泊松方程的表达式为:
<2Pn+1>i=(1-γ)
(1)
式中:γ是一个系数,取值范围为0~1,Lee等[22]建议取值为0.01≤γ≤0.05。
通过对上式进行离散,最终会得到一个关于压力的稀疏矩阵。而对该矩阵的求解则耗费了绝大部分的计算时间。因此,如何高效地求解稀疏矩阵是提高MPS方法计算效率的关键点。
2.3.1 稀疏矩阵的存储
非零元素的个数远远小于元素总数的矩阵被称为稀疏矩阵。一般来说,一个N阶矩阵需要使用N*N的数组来存放,由于零元素并不参与计算,但是数量又很多,这无疑会增加很多不必要的存储开销。因此,对于稀疏矩阵需要使用压缩存储,这不仅可以节省存储空间,同时也可以节省计算时间。但使用何种压缩格式,则需要结合具体问题和实现难易度进行考虑。
本文采用了CSR(行压缩)的存储格式。该格式需要三类数据来表达:数值,列号以及行偏移。数值和列号与完全存储时的情况一致,表示对应元素的值及其列号,行偏移则表示某一行的第一个非零元素在values里面的起始偏移位置。假设有如下稀疏矩阵:

如果采用zero-based索引的话,该矩阵的CSR存储可表示为:

2.3.2 矩阵求解
稀疏矩阵的求解是科学和工程计算中经常遇到的问题,因此,关于稀疏矩阵求解的研究也取得了很多进展。其中,向量乘法运算(SpMV)是一个关键操作,特别是使用迭代法求解时,矩阵向量的乘法运算对计算效率的影响尤为突出。而在GPU平台上实现稀疏矩阵向量乘法运算则更具有挑战性。这主要是因为稀疏矩阵存储格式对GPU访存的影响,非零元素的随机分布可以导致线程之间的计算负载不均衡。

图6 CPU+GPU并行方案图示 Fig.6 The schematic diagram of CPU+GPU
在CUDA的官方库中有一些成熟的线性代数库,最终使用CULA线性代数库来求解稀疏矩阵。CULA[24]是一个用GPU开发的线性代数求解工具集,能够求解稀疏矩阵和稠密矩阵,并能达到很可观的加速比。对于稀疏矩阵,CULA提供了各种常用的迭代方法,比如共轭梯度(CG)、双共轭梯度(BICG)、稳定双共轭梯度(BICGSTAB)等。本文计算所采用的迭代方法为稳定双共轭梯度法(BICGSTAB),这种解法在效率、精度以及稳定性上都有较好的表现。
2.4MPS的CPU+GPU并行方案小结
通过对MLParticle-SJTU求解器中各部分计算时间的分析得知,PartB(邻居粒子搜寻、核函数计算、粒子对列表构建)与PartD(稀疏矩阵系数生成与稀疏矩阵求解)耗时最多。本文详细讨论了这两个最耗时部分在GPU上的加速策略。图6描述了将这两个模块进行部分GPU化后整个MPS求解的计算流程。
3 计算与分析
以三维晃荡问题和三维溃坝问题为研究对象,验证CPU+GPU加速的可靠性与效率问题。其中,对于溃坝算例本文详细分析了CPU+GPU相对于单CPU串行时的加速情况。本节中两个算例所采用的计算平台均为高性能集群,该计算节点的配置为Intel(R) Xeon(R) CPU E5-2680 v2 @ 2.80GHz,十核心;内存64G;K40 M显卡,显存12G,具有2 880个CUDA计算核心。需要指出的是,后文中MLParticle-SJTU计算结果是指单线程串行计算结果,CPU+GPU计算结果则是指CPU串行加GPU并行(邻居粒子搜寻模块和泊松方程求解模块)的计算结果。
3.1三维溃坝模拟
本文计算所采用的溃坝模型如图7所示,水柱位于液舱的右侧,初始时刻在挡板的约束下处于静平衡状态,从t=0 s时刻开始自由运动。水柱前面有一个方形障碍物,为了记录水柱的演化过程,在x=0.992 m,z=0 m处设置了一个水面高度探测器H1,记录该位置处水面高度随时间变化曲线。在计算中,总共使用了1 015 793个粒子来模型化该算例,其中652 212为水粒子,其余为边界粒子,粒子初始间距为0.01 m。
图8给出了H1位置处水面高度随时间变化曲线,计算终止在t=4 s,其中实验结果来自文献[25]。从图中可以看到,在t=0.4 s左右,水柱前缘到达H1,此后H1位置处水面迅速上升,在t=1.8 s左右,水面出现一个较大的峰值,这是由于障碍物后面返回的水体经过H1。对比可以看到,数值计算给出的峰值与实验值有一点差别,但水面的整体变化趋势和实验结果是比较接近的。需要说明的是,该算例的流动现象是非常复杂的,自由面变形十分剧烈,对于这样的流动问题,数值和实验的完全吻合是十分困难的,尽管如此,整体上看,MLParticle-SJTU和CPU+GPU得到的计算结果与实验结果基本一致。

图7 溃坝的几何尺寸(单位:m)Fig.7 Geometry definition of Dam breaking(unit: m)
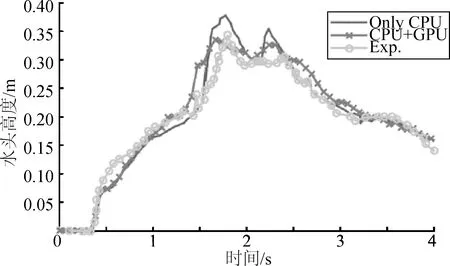
图8 H1位置处水面高度随时变化曲线Fig.8 The varying curve of elevating head at H1
3.2计算效率分析
对上节中的溃坝算例分别取五种不同的粒子间距来计算分析,具体参数如表2所示。此外,分析计算效率时采用的是计算中间100步的平均值。

表2 不同粒子间距及其对应的粒子数Tab.2 Varied particle spaces and corresponding particle number
3.2.1 邻居粒子加速情况
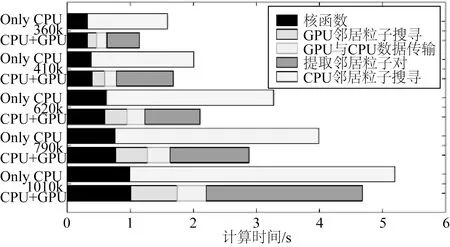
图9 不同粒子数下PartB各部分计算时间的分布变化 Fig.9 Time distribution of varied particle numbers in PartB
图9描述了PartB模块在MLParticle-SJTU与CPU+GPU模式下,五种不同粒子间距的时间分布情况。从整体上来说PartB的GPU+CPU加速效果并不明显,这是因为随着GPU加速的应用,邻居粒子搜寻在PartB中所占的比例相对较小,而随之产生的数据传输、提取邻居粒子对等额外操作所消耗的时间却占了较大比重。如果单独来比较GPU+CPU加速的邻居粒子搜寻和CPU串行时的邻居粒子搜寻,则可以发现采用GPU+CPU时有5~10倍的加速比。而诸如数据传输,特别是提取邻居粒子对这些额外操作耗费如此多的时间,主要是因为保存粒子信息的数组太大。比如,当粒子数为1 010 k时,拉普拉斯作用域内的邻居粒子对为101 447 855左右,而所需分配的显存大小为4 600 MB左右,如此庞大的数据量需要相当多的数据拷贝时间。同时,如此大的粒子对数也需要非常多的计算时间来提取邻居粒子对。但实际上,数据拷贝是对连续内存进行整段复制,因此这个效率相对还是较高的。而提取邻居粒子对则是对分散的数据(N个线程会产生N段数据,在GPU并行中,线程数一般是稍大于粒子数的,因此数据很分散)进行串行重排,因而相对来说耗时也要大许多。总之,数据传输以及粒子重排这些额外操作大大降低了加速效果。另外,核函数没有采用GPU加速也是考虑到这样做会进一步增加数据传输量。
由此可见,虽然GPU加速在邻居粒子搜寻中能提高数倍的计算效率,但CPU+GPU这种部分GPU化所产生的额外操作大大降低了加速效果。为了充分利用GPU加速可以采用如下改进措施:建立邻居粒子对信息时,可以将粒子间距稍微大于作用间距的粒子对也进行保存,而在需要使用邻居粒子对时则进一步检查是否是真正的邻居粒子。通过这种方法,可以对粒子对信息进行复用,只需在一定计算步数之后才更新邻居粒子对信息,从而减少数据传输以及串行重排的次数,具体算法可以参考Koshizuka[1]文章中的附录A。
3.2.2 泊松方程求解的加速情况
在MLParticle-SJTU串行计算时,泊松方程求解所占时间比例高达80%以上,因此有效的加速泊松方程求解对提高计算效率有相当大的意义。图10是五种不同粒子数下,使用GPU加速后泊松方程求解所对应的加速比。可以看到,加速比在6x~11x左右,随着粒子数的增多,加速比也有增大的趋势。此外,为了保证结果具有可比性,CPU+GPU与MLParticle-SJTU对稀疏矩阵求解的迭代精度是相当的。 值得一提的是,GPU计算时间是包括数据传输的。虽然需要交换的数据量不小,但是由于是整段内存拷贝传输,影响相对较小。

图10 不同粒子数下CPU+GPU与MLParticle-SJTU泊松方程求解计算时间的分布Fig.10 Time distribution of varied particle numbers of CPU+GPU and MLParticle-SJTU

图11 不同粒子数下CPU+GPU与MLParticle-SJTU 计算时间分布Fig.11 Time distribution of varied particle numbers of CPU+GPU and MLParticle-SJTU
3.2.3 GPU加速后的整体情况
在分析了PartB和泊松方程求解这些局部的加速情况后,有必要来看看整体时间分布的变化。在对五组数据进行分析后发现,时间占比较大的仍然是PartB和稀疏矩阵的求解,而其它部分所占时间则很少。为了方便起见,将PartB和稀疏矩阵求解之外的其它模块所耗时间合在了Others中进行比较分析。从图11中可以看到:1) 采用CPU并行技术能提高MPS的计算效率;2) 使用GPU加速后,PartB所占的比例增大到了30%左右,这是因为稀疏矩阵的求解时间大大减少了,PartB没有太大的改进,在加速后的时间占比中反而明显的增加了。
3.3晃荡算例
液舱的模型尺寸如图12所示,其中长L=0.79 m,高H=0.48 m,宽W=0.48 m。水深d=0.144 m,对应的充水率为30%。压力监测点在液舱右侧壁面自由面附近,距离液舱底部0.12 m。粒子总数达到了604 k,其中流体粒子422 k,其余为边界粒子。粒子的初始间距为0.005 m,时间步长为0.001 5 s,重力加速度g=9.81 m/s,水的密度为1 000 kg/m3。液舱的外部激励方程为:
x=-Acos(ωt)
(2)
式中:A为激励幅值,取0.057 5 m;ω为外部激励的圆频率,取4.49 rad/s。
图13给出了流动达到剧烈变化时,两个不同时刻的自由面形状。可以看到在流体到达右边顶部以及随后流体与右侧顶部冲击时,CPU+GPU和MLParticle-SJTU计算结果与实验所示的自由面形状都吻合良好。其中,实验数据源于Chang等[26]。
图14描述了MLParticle-SJTU和CPU+GPU给出的压力曲线能够较好的和实验相吻合。一次拍击有两个压力峰值,第一个压力峰值的产生是由于液体水平运动对侧壁撞击造成的,此后液体沿着舱壁向上运动,并在重力的作用下开始下落,从而对底部流体产生第二次拍击。
图15描述了晃荡算例的加速情况。其中,邻居粒子搜寻部分,CPU+GPU相较于MLParticle-SJTU有11.6x的加速比,但是由于数据传输和粒子重排所消耗的时间较多,导致PartB部分的加速只有1.4x;而在泊松方程求解这一块,加速比则有9.2x;最后,总体上的加速比则为3.2x。可以看到,晃荡算例所表现出的加速情况与溃坝算例中的结果是相当一致的。

图12 晃荡模型尺寸 Fig.12 Geometry definition of sloshing

图13 不同时刻粒子轮廓比较Fig.13 Comparison of free surface snapshots at different time

图14 P点拍击压力变化曲线对比Fig.14 The varying curve of impact pressure at point P

图15 晃荡算例加速情况(MLP即 MLparticle-SJTU)Fig.15 Time distribution of sloshing case (MLP is short for MLParticle-SJTU)
4 结 语
本文以CPU+GPU为计算平台,研究了GPU并行计算技术在三维MPS方法中的应用,并对晃荡、溃坝等典型自由面问题进行了数值模拟。通过计算结果与实验值比较,验证了CPU+GPU并行计算方式在求解水动力学问题中的可靠性与适用性。通过比较CPU+GPU与MLParticle-SJTU的计算时间,可以看到单步CPU+GPU能提高MPS的并行效率。在溃坝流动问题中,泊松方程求解的加速比最高可达11.0x。由此可见,CPU+GPU并行加速能够有效地提高三维MPS方法的计算效率。
在对MLParticle-SJTU中两个时间占比最大的模块,PartB和泊松方程的求解进行GPU加速后可以发现:虽然泊松方程的求解得到了较好的加速,但是PartB加速后的粒子重排与数据传输这些额外操作显著地增加了时间消耗,使得PartB的加速不明显,因而导致PartB在加速后的时间占比中显著增大,在一定程度上影响了整体的加速情况。如果要解决这个问题,可以考虑的途径有:1)对粒子信息进行复用,充分挖掘邻居粒子链表法这种存储模式的优点;2)考虑实现MPS的全GPU化,从而不再产生这些额外操作。
从整体上来说,CPU+GPU这种并行加速方式可以有效提高MPS的计算效率。但是由于在部分GPU化时会存在与原有程序进行拼接而产生额外的操作,有时这些额外的操作会降低整体的加速比。比如PartB中的邻居粒子搜寻就说明了额外操作会大大影响整体加速比。因此,在目前部分GPU化的基础上,将所有计算全部交由GPU处理,并根据GPU的特点充分地利用GPU的加速潜力。
[1] KOSHIZUKA S,NOBE A,OKA Y.Numerical analysis of breaking waves using the moving particle semi-implicit method[J].International Journal for Numerical Methods in Fluids,1998,26(7):751-769.
[2] 张雨新,万德成.用 MPS 方法数值模拟低充水液舱的晃荡 [J].水动力学研究与进展,2012,27(1):100-107.(ZHANG Y X,WAN D C.Numerical simulation of liquid sloshing in low-filling tank by MPS[J].Chinese Journal of Hydrodynamics,2012,27(1):100-107.(in Chinese))
[3] ZHANG Y X,TANG Z Y,WAN D C.A parallel MPS method for 3D dam break flows[C]//Proceedings of the 8th Int.Workshop on Ship Hydro.2013:135-139.
[4] IKARI H,GOTOH H.Parallelization of MPS method for 3D wave analysis[C]// Proceedings of the 8th International Conference on Hydro-science and Engineering (ICHE).2008.
[5] GOTOH H,KHAYYER A,Ikari H,et al.Refined reproduction of a plunging breaking wave and resultant splash-up by 3D-CMPS method[C]//Proceedings of the Nineteenth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2009:518-524.
[6] IRIBE T,FUJISAWA T,KOSHIZUKA S.Reduction of communication in parallel computing of particle method for flow simulation of seaside areas[J].Coastal Engineering Journal,2010,52(04):287-304.
[7] ZHANG Y X,YANG Y Q,TANG Z Y,et al.Parallel MPS method for three-dimensional liquid sloshing[C]// Proceedings of the Twenty-fourth International Ocean and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2014:257-264.
[8] HARADA T,KOSHIZUKA S,KAWAGUCHI Y.Smoothed particle hydrodynamics on GPUs[C]// Proceedings of the Computer Graphics International.2007:63-70.
[9] ZHANG Y X,SOLETHALER B,PAJAROLA R.GPU accelerated SPH particle simulation and rendering[C]// Proceedings of the ACM SIGGRAPH 2007 Posters.ACM,2007.
[10] CRESPO A J C,DOMINGUEZ J M,BARREIRO A,et al.GPUs,a new tool of acceleration in CFD:efficiency and reliability on smoothed particle hydrodynamics methods[J].PLoS One,2011,6(6):e20685.
[11] DOMíNGUEZ J M,CRESPO A J C,Gómez-Gesteira M.Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method[J].Computer Physics Communications,2013,184(3):617-627.
[12] HORI C,GOTOH H,IKARI H,et al.GPU-acceleration for moving particle semi-implicit method[J].Computers & Fluids,2011,51(1):174-183.
[13] 朱小松.粒子法的并行加速及在液体晃荡研究中的应用 [D].大连:大连理工大学,2011.(ZHU X S.Parallel acceleration of particle method and its application on the study of liquid sloshing [D].Dalian :Dalian University of Technology.(in Chinese))
[14] TANG Z Y,WAN D C.Numerical simulation of impinging jet flows by modified MPS method[J].Engineering Computations,2015,32(4):1 153-1 171.
[15] ZHANG Y X,WAN D C,TAKANORI H.Comparative study of MPS method and level-set method for sloshing flows[J].Journal of Hydrodynamics,Ser.B,2014,26(4):577-585.
[16] 张雨新,万德成,日野孝则.MPS方法数值模拟液舱晃荡问题[J].海洋工程,2014,32(4):24-32.(ZHANG Y X,WAN D C,HINO T.Application of MPS method in liquid sloshing[J].The Ocean Engineering,2014,32(4):24-32.(in Chinese))[17] 杨亚强,唐振远,万德成.基于MPS方法模拟带水平隔板的液舱晃荡[J].水动力学研究与进展,2015,30(2):146-153.(YANG Y Q,TANG Z Y,WAN D C.Numerical study on liquid sloshing in horizontal baffled tank by MPS method[J].Chinese Journal of Hydrodynamics,2015,30(2):146-153.(in Chinese))
[18] 张雨新,万德成.MPS方法在二维液舱晃荡中的应用[J].复旦学报:自然科学版,2013,52(5):618-626.(ZHANG Y X,WAN D C.Application of MPS method for 2D liquid sloshing[J].Journal of Fudan Univesity,Natural Science,2013,52(5):618-626.(in Chinese))
[19] 张驰,张雨新,万德成.SPH方法和MPS方法模拟溃坝问题的比较分析[J].水动力学研究与进展,2011,26(6):736-746.(ZHANG C,ZHANG Y X,WAN D C.Comparative study of SPH and MPS methods for numerical simulations of dam breaking problems[J].Chinese Journal of Hydrodynamics,2011,26(6):736-746.(in Chinese))
[20] 张雨新,万德成.MPS 方法在三维溃坝问题中的应用[J].中国科学物理学力学天文学,2011,41(2):140-154.(ZHANG Y X,WAN D C.Application of MPS in 3D dam breaking flows[J].Scientia Sinica Physica,Mechanica & Asstronomica,2011,41(2):140-154.(in Chinese))
[21] CUDA_C_Programming_Guide[R].NVIDIA,CUDA Toolkit Doc,2015.
[22] LEE B H,PARK J C,KIM M H,et al.Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads[J].Computer Methods in Applied Mechanics and Engineering,2011,200(9):1 113-1 125.
[23] DOMINGUEZ J M,CRESPO A J C,GóMEZ-GESTEIRA M,et al.Neighbour lists in smoothed particle hydrodynamics[J].International Journal for Numerical Methods in Fluids,2011,67(12):2 026-2 042.
[24] CULA (GPU-Accelerated LAPACK)[ED/OL].http://www.culatools.com/.
[25] KLEEFSMAN K,FEKKEN G,VELDMAN AEP,et al.A volume-of-fluid based simulation method for wave impact problems[J].Journal of Computational Physics,2005,206(1):363-393.
[26] SONG Y K,CHANG K A,RYU Y,et al.Experimental study on flow kinematics and impact pressure in liquid sloshing[J].Experiments in Fluids,2013,54(9):1-20.
Application of GPU acceleration techniques in 3D violent free surface flows
LI Haizhou1,2,TANG Zhenyuan1,2,WAN Decheng1,2
(1.State Key Laboratory of Ocean Engineering,School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; 2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)
O353
A
10.16483/j.issn.1005-9865.2016.05.003
万德成。 E-mail:dcwan@sjtu.edu.cn
1005-9865(2016)05-0020-10
2015-10-26
国家自然科学基金资助项目(51379125,51490675,11432009,51579145,11272120);长江学者奖励计划(T2014099);上海东方学者岗位跟踪计划(2013022);工信部数值水池创新专项VIV/VIM项目(2016-23/09)
李海洲(1991-),男,硕士,主要从事GPU并行技术在无网格粒子法中的应用。E-mail:dxlhz@foxmail.com

