Rosenau-KdV方程的一个非线性守恒加权差分逼近

陈利娅，胡劲松*

(西华大学理学院，四川成都　610039)



Rosenau-KdV方程的一个非线性守恒加权差分逼近

陈利娅，胡劲松*

(西华大学理学院，四川成都610039)

利用LXA加权差分格式的构造思想，在空间层引入加权系数，对Rosenau-KdV方程的初边值问题进行数值研究，提出了一个三层非线性加权差分格式，合理模拟了该问题的两个守恒性质，得到了差分解的先验估计，并利用离散泛函分析方法分析了格式的二阶收敛性与无条件稳定性.数值实验表明，该方法是可靠的，且适当调整加权系数可以大幅提高计算精度.

Rosenau-KdV方程；差分格式；守恒；收敛性；稳定性

在描述紧离散系统的动力学行为时，Rosenau方程：

(1)

一经提出就引起了众多学者的关注[1-7].作为非线性波的进一步考虑，对Rosenau方程(1)添加粘性项uxxx，则得到Rosenau-KdV方程[8]：

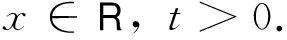
(2)

文献[8]讨论了Rosenau-KdV方程(2)的孤波解和周期解，文献[9-11]进一步给出了带通常的幂指数非线性项的广义Rosenau-KdV方程的孤波解以及两个守恒量.

本文考虑如下Rosenau-KdV方程的初边值问题:

(3)

(4)

(5)

其中u0(x)是已知光滑函数.由于Rosenau-KdV方程(2)的单个孤波解[8]为：

即Rosenau-KdV方程(2)的物理边界满足：

因此，当-xL≫0,xR≫0时，初边值问题(3)～(5)与Rosenau-KdV方程(2)的Cauchy问题是一致的，故边界条件(5)的假设是合理的.问题(3)～(5)具有如下守恒律[12]：

(6)

(7)

其中Q(0),E(0)均为仅与初始条件有关的常数.

文献[12]对初边值问题(3)～(5)提出了一个具有二阶精度的三层线性守恒差分格式，且模拟了守恒量(6)和(7)；文献[13,14]进一步对一类广义Rosenau-KdV方程提出了两层和三层有限差分格式，但它们都只能模拟守恒量(7).本文在保持二阶理论精度的前提下，利用LAX加权格式的构造思想，在空间层引入加权系数θ，对初边值问题(3)～(5)构造了一个具有二阶精度的含有加权系数的非线性差分格式，该格式合理模拟了守恒量(6)和(7)，通过适当调整加权系数θ，可以使计算精度大幅度提高，且计算效果明显优于文献[12]中的二阶格式.

1　差分格式及守恒律

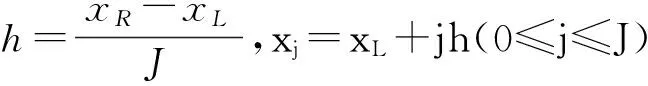
用C表示与τ和h无关的一般正常数(即在不同地方有不同的取值)，并定义如下记号：

(8)

(9)

(10)

为便于分析，定义

则差分格式(8)～(10)对守恒量(6)和(7)的数值模拟如下：

定理1差分格式(8)～(10)关于以下离散能量是守恒的，即

(11)

(12)

其中，n=1,2,…,N.

证明将(8)式两端乘以h然后对j从1到J-1求和，考虑到边界条件(10)以及分部求和公式[15]可得

(13)

由Qn的定义，将(13)式递推即可得(11)式.

(14)

又因为

(15)

(16)

所以，由En的定义，将(15)和(16)式代入(14)式，然后递推即可得(12)式.】

2　差分格式的收敛性与稳定性

下面在先验估计的基础上，运用离散泛函分析方法讨论差分解的收敛性和稳定性.

差分格式(8)～(10)的截断误差定义如下：

(17)

(18)

(19)

由Taylor展开可知，当h,τ→0时，

引理1[12]设u0∈H2[xL,xR]，则初边值问题(3)～(5)的解满足：

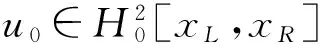
从而有

证明由于

(20)

所以由定理1可得

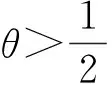
再由Cauchy-Schwarz不等式,有

(21)

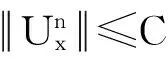
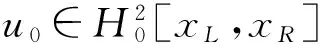
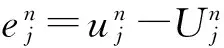
(22)

(23)

(24)

(25)

类似于(15)式有

(26)

利用引理1、定理2以及Cauchy-Schwarz不等式，有

(27)

(28)

将(26)～(28)式代入(25)式，并结合(21)式，整理得

(29)

令

对(29)式两端同时乘以τ，然后从0到n-1求和得：

(30)

由于B0=O(τ2+h2)2，且

所以类似于(20)式，有

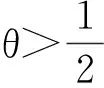
于是由离散Gronwall不等式[15]，有

再类似(21)式，有

最后由离散Sobolev不等式[15]，有

与定理3类似，可以证明：

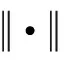
3　数值实验

在数值实验中，取初值函数为：

固定xL=-70,xR=100,T=40.为了便于比较，记本文的加权格式为格式1(表1和表2中仅用加权系数θ的值来表示)，记文献[12]中的三层线性格式为格式2.就τ和h的不同取值，分别列出了t=20和t=40两个时刻格式1在加权系数θ取不同值时的误差和格式2的误差进行比较，结果见表1和表2；加权系数取0.5和1.0两种情形下的守恒量Qn和En的部分数据见表3和表4.

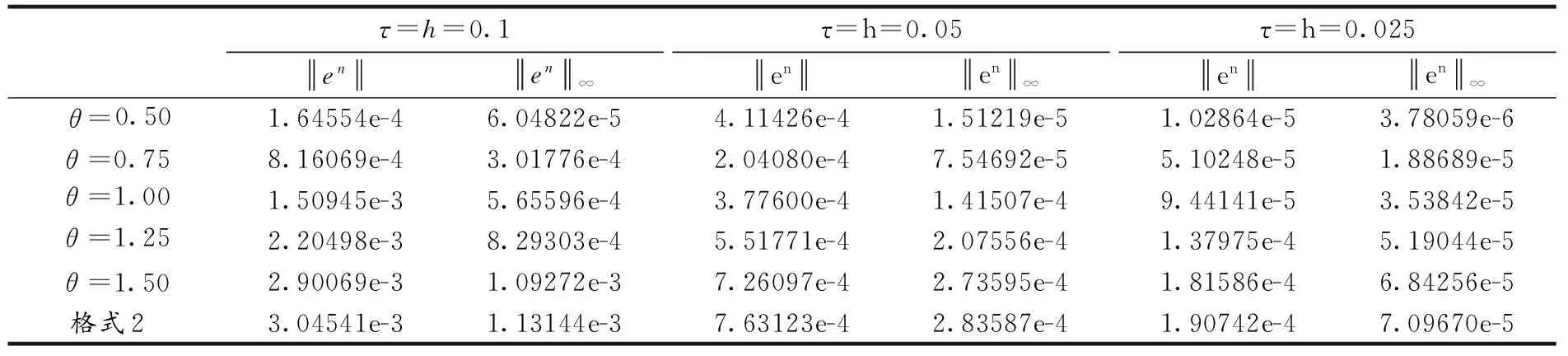
表1　t=20时，格式1在不同参数下的误差和格式2的误差比较

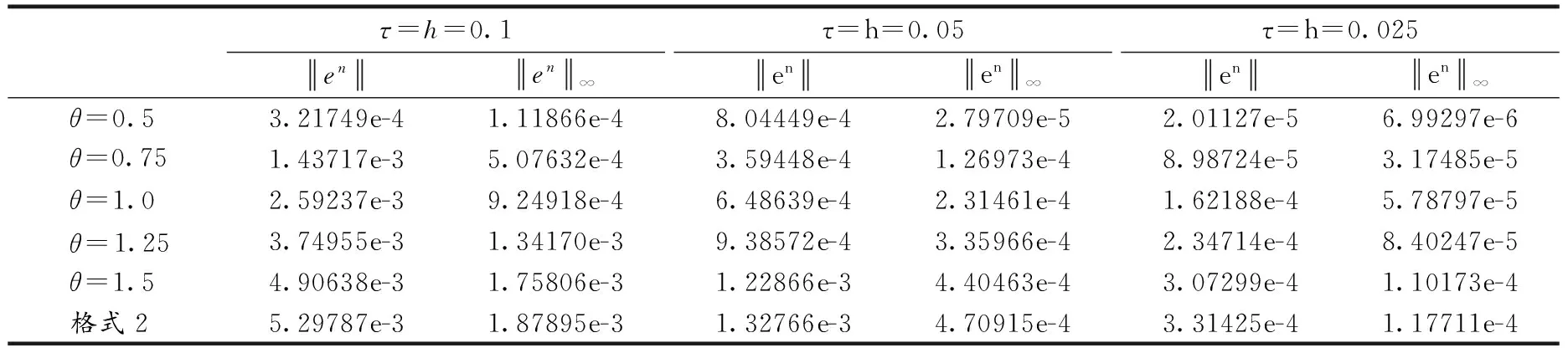
表2　t=40时，格式1在不同参数下的误差和格式2的误差比较

表3　θ=0.5时，格式1的守恒量Q n和E n的部分数据

表4　θ=1.0时，格式1的守恒量Q n和E n的部分数据

从数值结果可以看出，本文格式明显具有二阶精度；随着加权系数(θ>0.5)逐步增大，数值解的误差也随之增大；加权系数θ取0.5时计算效果最好，相对于文献[12]中的三层线性差分格式，其计算精度提高了一个数量级.另外，格式也对守恒量(6)和(7)进行了高精度模拟，故本文对初边值问题(1)～(3)提出的加权格式是可靠的.

[1]ROENAUP.Aquasi-continuousdescriptionofanonlineartransmissionline[J].Physica Scripta,1986,34:827.

[2]ROSENAU P.Dynamics of dense discrete systems[J].ProgressofTheoreticalPhysics,1988,79:1028.

[3]PARK M A.On the Rosenau equation[J].AppliedMathematicsandComputation,1990,9(2):145.

[4]CHUNG S K,HA S N.Finite element Galerkin solution for the Rosenau equation[J].ApplicableAnalysis,1994,54(1/2):39.

[5]OMRANI K,ABIDI F,ACHOURI T,et al.A new conservative finite difference scheme for the Rosenau equation[J].AppliedMathematicsandComputation,2008,201(1/2):35.

[6]CHUNG S K.Finite difference approximate solutions for the Rosenau equation [J].ApplicableAnalysis,1998,69(1/2):149.

[7]CHUNG S K ,PANI A K.Numerical methods for the Rosenau equation[J].ApplicableAnalysis,2001,77(3/4):351.

[8]ZUO J.Solitons and periodic solutions for the Rosenau-KdV and Rosenau-Kawahara equations[J].AppliedMathematicsandComputation,2009,215(2):835.

[9]ESFAHANI A.Solitary wave solutions for generalized Rosenau-KdV equation[J].CommunicationinTheoreticalPhysics,2011,55(3):396.

[10]RAZBOROVA P,TRIKI H,BISWAS A.Perturbation of dispersive shallow water waves[J].OceanEngineering,2013,63:1.

[11]EBADI G,MOJAVER A,TRIKI H,et al.Topological solitons and other solutions of the Rosenau-KdV equation withe power law nonlinearity[J].RomanianJournalofPhysics,2013,58(1/2):1.

[12]HU J,XU Y,HU B.Conservative linear difference scheme for Rosenau-KdV equation [J].AdvancesinMathematicalPhysics,2013(2013),Article ID 423718,7 pages.

[13]LUO Y,XU Y,FENG M.Conservative difference scheme for generalized Rosenau-KdV equation[J].AdvancesinMathematicalPhysics,2014(2014),Article ID 986098,7 pages.

[14]ZHENG M,ZHOU J.An average linear difference scheme for the generalized Rosenau-KdV equation[J].JournalofAppliedMathematics,2014(2014),Article ID 202793,9 pages.

[15]ZHOU Yu-lin.ApplicationofDiscreteFunctionalAnalysistotheFiniteDifferenceMethods[M].Beijing:International Academic Publishers,1990.

(责任编辑马宇鸿)

A weighted nonlinear conservative difference scheme for Rosenau-KdV equation

CHEN Li-ya,HU Jin-song

(School of Science,Xihua University,Chengdu 610039,Sichuan,China)

In this paper,a finite difference method for an initial-boundary value problem of Rosenau-KdV equation is considered.A nonlinear three-level conservation finite difference scheme with weighted coefficient is designed by LAX scheme.The scheme simulates two conservation properties of the problem well.The prior estimates of the finite difference solution are also obtained.It is proved that the finite difference scheme is convergent with second-order and unconditionally stable by discrete functional analysis method.Numerical experiment also shows that appropriate adjustments to the weighted parameter would significantly improve the computational accuracy.

Rosenau-KdV equation;difference scheme;conservative;convergence;stability

10.16783/j.cnki.nwnuz.2016.05.005

2016-01-14;修改稿收到日期:2016-04-01

四川省教育厅重点科研基金资助项目(16ZA0167)；西华大学重点科研基金资助项目(Z1513324)

陈利娅(1972—)，女，四川新都人，副教授.主要研究方向为偏微分方程数值解.E-mail:chenliya-1@163.com

*通讯联系人，男，教授，博士.主要研究方向为偏微分方程数值解.E-mail:hjs888hjs@163.com

O 241.82

A

1001-988Ⅹ(2016)05-0018-06