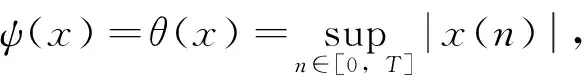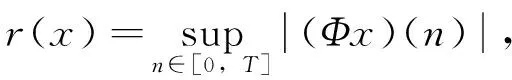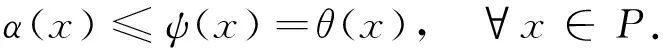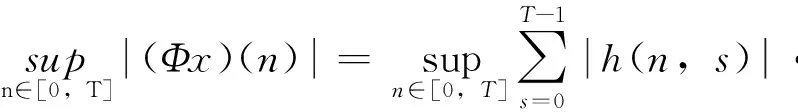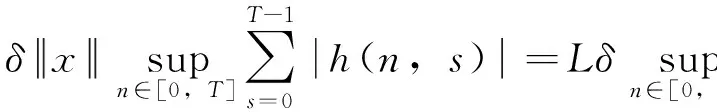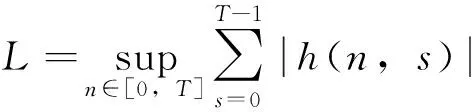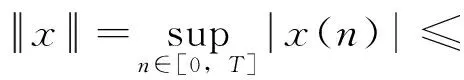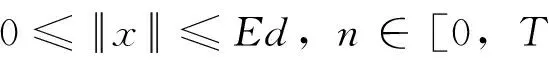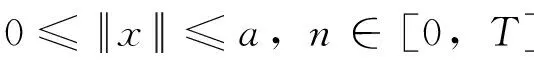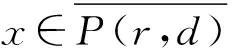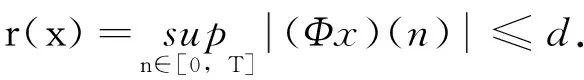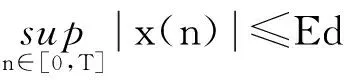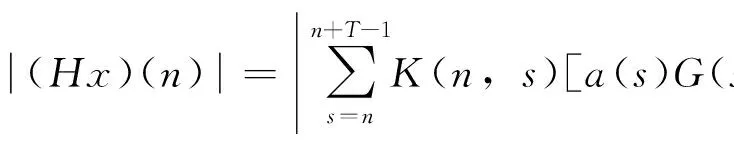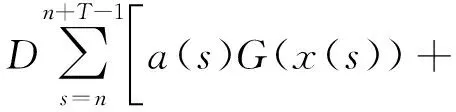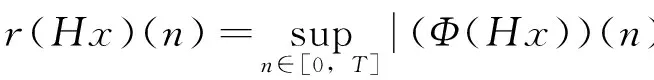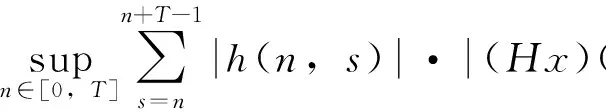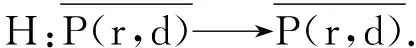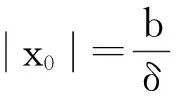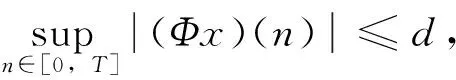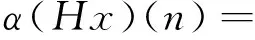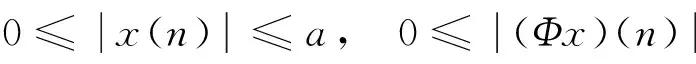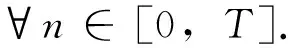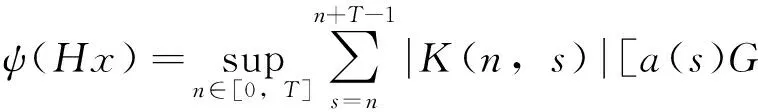一类中立型差分方程的三重正周期解
王丽丽,胡 猛
(安阳师范学院 数学与统计学院,河南安阳 455000)
一类中立型差分方程的三重正周期解
王丽丽,胡猛
(安阳师范学院 数学与统计学院,河南安阳455000)
研究了一类中立型差分方程,运用锥多重不动点理论(Avery-Peterson不动点理论),给出了其至少存在三个正周期解的充分条件.
中立型差分方程;正周期解;锥不动点
用差分方程描述的离散模型在许多领域有着广泛的应用,如生态系统中离散种群模型比连续模型能更好地模拟当种群各代不相重叠时的情形.由于计算机的实际运算与操作需要将微分方程离散化,而低维截面上的离散映像可以反映高维连续过程的一些规律,所以近年来,差分方程得到了学者的广泛关注[1-5],但有关中立型差分方程多重正周期解的存在性研究还很少.
考虑如下中立型差分方程:
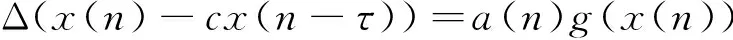
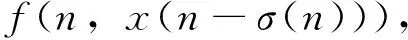
(1)
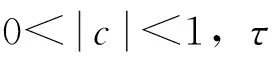
本文运用Avery-Peterson锥不动点定理,研究方程(1)的多重正周期解的存在性,并给出其至少存在三个正周期解的充分条件.
对于方程(1),假设:
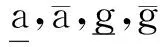
(A2)函数f(n,x)关于第二变元x是非减的.
1 预备知识
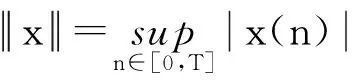
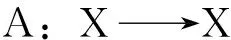
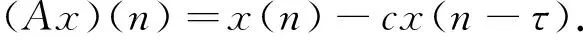
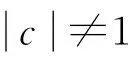
由引理1及A与A-1的定义可得,
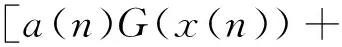
(2)
其中
引理2x(n)是方程(2)的T-周期解,当且仅当(A-1x)(n)是方程(1)的T-周期解.
类似文献[8]中引理3的证明,可得
引理3x(n)是方程(2)的一个T-周期解,当且仅当x(n)是方程
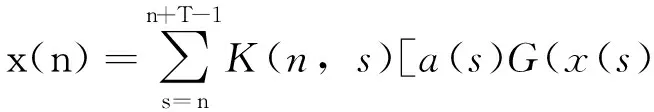
的一个T-周期解,其中
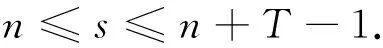
由条件(A1)可得0 引理4[9]如果c∈(-δ,0],x∈P,那么有 证明对∀x∈P,有(Hx)(n+T)=(Hx)(n),所以Hx∈X.对∀x∈P,有 由引理4及c∈(-δ,0]可知G(x(n))≥0,n∈Z.因此, 又因为 记集合 设r,θ是P上非负连续凸泛函,α是P上非负连续凹泛函,ψ是P上非负连续函数,对于正实数a,b,c,d,定义下面的凸集: 和一个闭集 定理1[10]设r,θ是P上非负连续凸泛函,α是P上非负连续凹泛函,ψ是P上非负连续泛函,满足ψ(ρx)≤ρψ(x),0≤ρ≤1,且存在正数E,d,使得 (3) (i){x∈P(r,θ,α,b,c,d):α(x)>b}≠∅,α(Hx)>b,x∈P(r,θ,α,b,c,d); (ii)α(Hx)>b,∀x∈P(r,α,b,d),θ(Hx)>c; (iii)0∉R(r,ψ,a,d),当x∈R(r,ψ,a,d)时ψ(Hx) 定义η,l∈[0,T],η≤l.设非负连续凹泛函α、非负连续凸泛函r,θ及非负连续函数ψ在锥P上的定义分别为 其中 显然,上面定义的函数满足 证明对∀x∈P,有 另外,对于任意的x∈P,有 (4) 并且ψ(ρx)=ρψ(x),∀ρ∈[0,1],∀x∈P.由(4)式可知定理1中的条件(3)成立. 定理2假设条件(A1)~(A2),(S1)~(S2)成立,c∈(-δ,0],则方程(1)至少存在三个正的T-周期解x1,x2,x3,且满足 那么 即 由条件(A2),(S2)及引理4,得 其次,由锥P的定义,得 由(A2),(S3)及引理4,得 所以,定理1中的条件(iii)成立. 综上所述,由定理1可得算子H至少存在三个不动点,即方程(2)至少存在三个正的T-周期解.再由引理2,方程(1)至少存在三个正的T-周期解.】 [1]AGARWAL R P,ZHANG W N.Periodic solutions of difference equations with general periodicity[J].ComputMathAppl,2001,42:719. [2]FAN M,WANG K.Periodic solutions of a discrete time nonautonomous ratio-dependent predator prey system[J].MathComputModel,2002,35:951. [3]LALLI B S,ZHANG B.On existence of positive solutions and bounded oscillations for neutral difference equations[J].JMathAnalAppl,1992,166:272. [4]PEICS H.Positive solutions of neutral delay difference equation[J].NoviSadJMath,2005,35(2):111. [5]ZENG X Y,SHI B,GAI M J.A discrete periodic Lotka-Volterra system with delays[J].ComputMathAppl,2002,47:491. [6]LU Shi-ping,GE Wei-gao.Periodic solutions of neutral differential equation with multiple deviating arguments[J].ApplMathComput,2004,156:705. [7]ZHANG Mei-rong.Periodic solution of linear and quasilinear neutral functional differential equations[J].JMathAnalAppl,1995,189:378. [8]申淑媛.具有反馈控制和时滞变量的离散周期系统周期解的存在性[J].华南师范大学学报(自然科学版),2007,3:14. [9]WU Jun,LIU Yi-cheng.Two periodic solutions of neutral difference systems depending on two parameters[J].JMathAnalAppl,2007,206:713. [10]AVERY R I,PETERSON A C.Three positive fixed points of nonlinear operators on ordered Banach spaces[J].ComputMathAppl,2001,42:313. (责任编辑马宇鸿) Triple positive periodic solutions for a class of neutral difference equation WANG Li-li,HU Meng (School of Mathematics and Statistics,Anyang Normal University,Anyang 455000,Henan,China) This paper is concerned with a class of neutral difference equation,by using a multiple fixed point theorem(Avery-Peterson fixed point theorem) in cones,several sufficient conditions are established for the existence of at least three positive periodic solutions for the equation. neutral difference equation;positive periodic solution;fixed point in cones 10.16783/j.cnki.nwnuz.2016.05.004 2016-01-11;修改稿收到日期:2016-03-30 河南省高等学校重点科研项目(16A110008,15A110004) 王丽丽(1981—),女,河南新乡人,讲师,硕士.主要研究方向为泛函微分方程理论及其应用. E-mail:ay_wanglili@126.com O 175.1 A 1001-988Ⅹ(2016)05-0014-04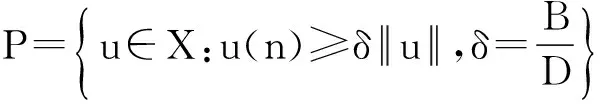
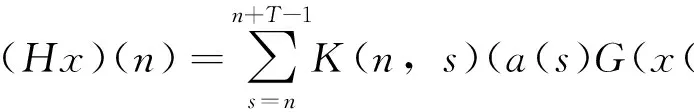
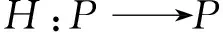
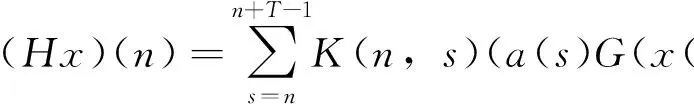
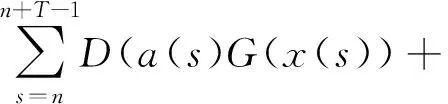
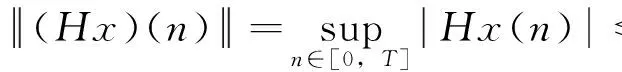
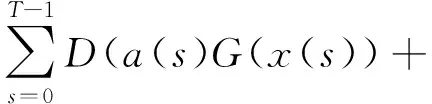
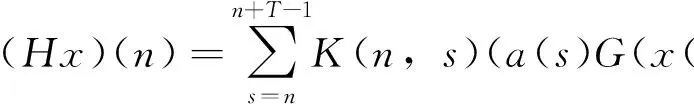
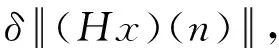
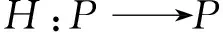

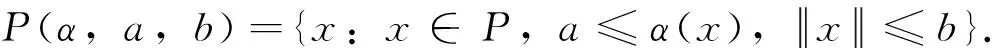
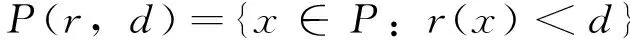
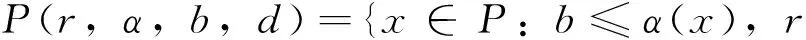
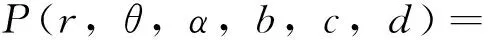
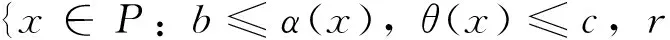
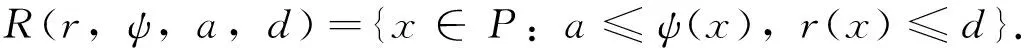
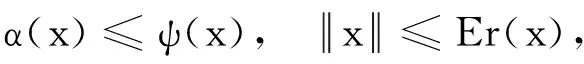
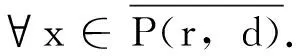
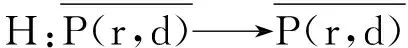
2 主要结果