基于风压差翻转漂移模型的海上搜寻区域确定

， ,

(1．中国科学院 沈阳自动化研究所， 沈阳 110016； 2．中国科学院大学， 北京 100049；3．中国科学院 光电信息处理重点实验室， 沈阳 110016)

基于风压差翻转漂移模型的海上搜寻区域确定

郑宏喆1,2,3，赵怀慈1,3,王立勇1,3

(1．中国科学院沈阳自动化研究所，沈阳110016； 2．中国科学院大学，北京100049；3．中国科学院光电信息处理重点实验室，沈阳110016)

为提高海上搜救的成功率，最大限度地减少生命和财产损失，需获得精确的漂移模型，并快速确定包含搜救目标的最小搜寻区域。对此，分析海洋环境、目标漂移特性等因素的不确定性对漂移运动的影响，提出一种新的风压差翻转率计算方法,并运用该方法建立搜救目标漂移模型。通过仿真试验，基于所建立的漂移模型，分别用解析法和Monte Carlo法对失事船舶搜寻区域进行估计。结果表明：风压差翻转率计算方法可提高漂移模型的精度；基于所建立的漂移模型，使用Monte Carlo法估计的搜寻区域能最大程度地包含搜救目标且面积小。

海上搜救；漂移模型；风压差翻转率；搜寻区域

Abstract: In order to improve Probability Of Success (POS) of Search And Rescue (SAR) operations and reduce the losses of life and property to the maximum extent, an accurate drift model is needed to determine minimum search area of objects being adrift quickly. A new method to compute leeway-jibing rate, which is used to develop the drift model of objects, is proposed for analyzing the impact of the marine environment uncertainties, and drift characteristics of the object etc. on the drift motion. With the drift model established，the search area of a wrecked vessel is estimated employing analytical method and Monte Carlo method by simulation. The results of the study show that the calculation method of leeway-jibing rate improves the accuracy of the drift model, and the search area estimated via Monte Carlo method is much smaller and contains the target object as far as possible.

Keywords: maritime search and rescue; drift model; leeway-jibing rate; search area

随着经济贸易的发展和海洋开发战略的实施，远洋运输、捕捞及海上石油勘探等活动日益频繁，发生水上险情和事故的频率与日俱增。发生海难时，为最大限度地减少生命和财产损失，需准确、快速地估计搜寻区域，进而提高海上搜救的成功率。准确地划定搜寻区域包含以下2个要求[1]：

(1)搜寻区域以最大概率包含搜救目标；

(2)搜寻区域尽可能细致，尽可能小，使搜寻力量在最短的时间内搜寻可能性最高的区域。

为使搜寻区域满足以上2个要求，需建立精确、简单实用的漂移模型。影响漂移模型的主要因素是风和流。流场数据既可通过实时实地观测获得，也可通过建立海洋水动力数学模型计算获得，可直接用于计算漂移轨迹。风对漂移运动的影响称为风压差，与漂浮物的种类有关，测量相对困难。因此，对漂移模型的研究主要集中在风压差上。早期采用间接法测量风压差，测量结果不精确。随着测量技术不断进步，测量装置变得小而灵活，从20世纪80年代开始，几乎所有有关搜救物体的试验都采用直接测量技术。[2]BREIVIK 等[3]通过观察和记录63种物体的漂移运动，得到风压差和风速的关系。基于此，挪威气象局(Norwegian Meteorological Institute，NMI)开发针对船舶和海上油污的漂移模型，该模型广泛应用于海上搜救中心及海上交通服务等部门。ISOBE等[4]通过水槽试验研究物体的漂移运动，推导出风压差计算式。ALLEN[5]通过统计分析试验数据发现风压差与海面10 m风速有着稳定的线性关系，并将风压差分解为顺风向分量和横风向分量。

事实上，海上漂浮物的运动存在很大的偶然性。NI等[6]提出预测船漂移的理论模型，根据船漂移特性和外部力场的不确定性区间分析估计搜寻区域。WANG等[7]考虑漂浮物的形状特征，并设计权值向量描述形状特征与随机运动之间的关系，提高平均漂移速度的估计精度。VANDENBULCKE等[8]使用超集合技术对直接或间接与漂移相关的同一物理过程的不同模型进行线性和非线性组合，通过运用数据同化、最小二乘等方法优化模型权值，最终得到最优的线性组合模型。BREIVIK等[9]采用Monte Carlo法在估计的事故位置附近产生符合某种概率分布的粒子群，对每个粒子进行漂移计算，停止时刻粒子群的凸包就是搜寻区域；该方法考虑了风速、流速、风压差和漂浮物初始位置的不确定性。

以上对漂移模型的研究中风压差一直在风向的左侧或右侧，而实际中搜救目标的风压差方向会从风向右侧突变到左侧或从左侧突变到右侧，这种现象被称为风压差翻转。文献[9]认为在恶劣天气下，受破碎波、强阵风的影响，搜救目标的风压差方向会突变；在极低或极高风速下，风压差容易翻转；在中等风速下，翻转的可能性较小。夏宇亮[10]将风压差每小时内翻转的概率设定为常数，预测漂浮物的漂移轨迹。目前有关风压差翻转的研究甚少，主要原因是风压差翻转的原因尚不明确、风压差速度方向改变不易测量及没有行之有效的统计方法确定风压差翻转的概率。这里对风压差翻转问题进行初步探索，建立含有风压差翻转的漂移模型，并选取恰当的方法估计搜寻区域。

1 搜救目标漂移模型

搜救目标的漂移运动是风、浪、流共同作用的结果。根据文献[11]的研究，当目标长度远小于海浪波长时，浪的影响可忽略。这里针对尺寸小的漂浮物进行研究，只考虑风和流的影响。

1.1 风压差翻转模型

由于搜救目标形状不规则，致使风作用在其水上部分时受力不对称，从而引起目标偏离风向漂移。目标偏离风向的角度称为风压差角。风压差与物体类型、浸没比等有关，将其分解为顺风向分量和横风向分量(见图1，其中Vw为风速)。风压差分解式为

Ld=adw10+bd

(1)

Lc+=ac+w10+bc+

(2)

Lc-=ac-w10+bc-

(3)

式(1)～式(3)中：w10为海面10 m风速；Lc+为风向右侧横风向分量，Lc-反之，通常Lc+和Lc-关于风速对称；ad，bd，ac+，bc+，ac-及bc-为通过拟合实际测量数据得到的线性系数，称为风压系数。美国和加拿大等国家通过对大量试验数据进行分析，拟合得到风压系数的经验值。

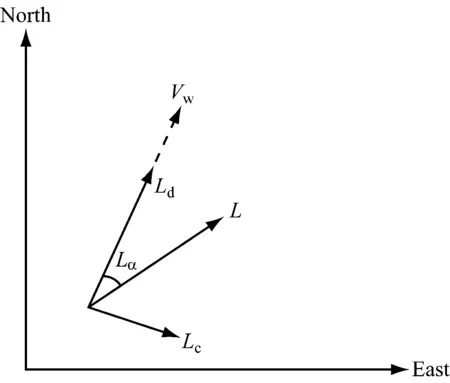
图1 风压差矢量分量

在现有的漂移模型研究中，风压差一直在风向的左侧或右侧，没有考虑风压差翻转的情况。考虑到漂移模型的影响因素为风、浪、流和目标漂移特性，风压差翻转必然与这些因素有关。水流作用于目标的水下部分，且流速通常相对稳定。因此，将风和流看成2种性质不同的作用力，彼此互不影响，即风压差翻转与流速无关。若对较小的物体进行研究，忽略浪的影响，则风压差翻转主要与风速、目标漂移特性有关。

风速突然改变的瞬间，目标运动的不确定性变大，风压差容易发生翻转。风速改变包括风向和大小的改变。为便于度量风速改变量，将风向和风幅的改变量归一化。风向的改变即为两向量的夹角，取值范围为[0，π]，可将风向改变量的归一化参数设为π。归一化以后的风幅和风向改变量Δw及Δφ分别为

Δw=‖Vw(n)-Vm(n-1)‖/b

(4)

Δφ=|φw(n)-φw(n-1)|/π

(5)

式(4)和式(5)中；b为风幅阈值；φw为风向。

目标漂移特性的作用决定漂移速度，因此建立目标漂移速度与风压差翻转之间的联系。目标漂移速度越小，对外界环境的改变越敏感，运动方向就越容易发生改变。目标漂移速度对风压差翻转的影响δ0表示为

δ0=a/‖V0(n)‖

(6)

式(6)中：a为目标漂移速度阈值。

风压差翻转率Lre为风向改变量Δw、风幅改变量Δφ及目标漂移速度对风压差翻转的影响δ0的加权和，即

Lre(n)=aδ0+βΔw+rΔφ

(7)

式(7)中：α，β及r分别为目标速度、风幅和风向影响的权重。当α=β=r=0时，Lre=0，将这种情况定义为不考虑风压差翻转。设翻转率阈值为τ，当Lre>τ时发生翻转，反之不翻转，即

(8)

若Lc+和Lc-关于风速对称，则风压差L(n)为

L(n)=Ld(n)+Lc(n)

(9)

1.2 漂移模型

目标漂移运动的作用力中，只考虑风和流。目标受力可表示为

(m+m)′dV0/dt=∑F=Fw=Fc

(10)

式(10)中：V0为目标漂移速度；∑F为目标所受外力之和；Fw和Fc分别为风、流的作用力；m为目标质量；m′为附加质量，来自于附着在目标表面的水的质量。

根据文献[12]的研究，目标初始漂移时速度在风、流等外力作用下急剧增加，在2～10 min之内达到某一恒定值，此后保持不变，加速度为零。因此，当预测目标几个小时或更长时间之后的位置时，加速过程所用时间远远短于总漂移时间，不予考虑，这就意味着不必知道目标质量m。

根据以上受力分析，目标的漂移速度是风压差与总水流速度之和(见图2)。已知当地风场和流场数据，目标的漂移轨迹可被预测。目标漂移速度计算式为

(11)

式(11)中：Vc为总水流速度；Vsc为海流；Vwc为风生流[13]，是风持续作用在水面上形成的，目前风对形成当地风生流的实际影响不是很清楚。一些海流数值预报模式数据已包括基于风的预报的当地风的影响，因此搜救计划者不必在预测的海流中加入当地风生流。此外，从海图或水文图册中得到的存在持续风区域的海流也不应把风生流计算在内。据此，目标漂移模型为

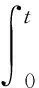
(12)

式(12)中：P0为目标初始位置；Pt为目标时刻的位置；t′为积分变量。

图2 目标漂移速度矢量计算

1.3 不确定性分析与处理

可靠的漂移模型需高时空分辨率和高精度的风场、流场数据，而搜救计划者所获取数据的质量往往不能满足预期要求。事故位置往往是不确定的，有时事故时间也是未知的，甚至最后已知位置也不确定。搜救目标的漂移特性存在估计误差。因此，精确的漂移模型要尽可能多地考虑以上各种不确定性。通过对风场、流场和风压差分解参数加入扰动项作为对不确定性的处理。

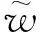
(13)

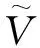
(14)

风压差分解公式中，线性回归系数的扰动项εd服从正态分布，则

(15)

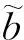
(16)

3 估计搜寻区域

目标的漂移运动存在很大的随机性，虽然漂移模型无法得到目标的精确位置，但可估计搜救目标可能存在的区域(即估计搜寻区域)。实际应用中，估计搜寻区域的方法有解析法和Monte Carlo法。

3.1 解析法

解析法的基本思想是尽量包含搜救目标可能存在的区域。首先，分别在最左和最右2个风压差角下进行漂移计算，得到左右漂移范围(可选择为圆、椭圆或矩形)；随后，对左右2个漂移范围进行最小面积覆盖，得到的区域即为搜寻区域。

以漂移范围为圆为例(见图3)，首先将左右漂移范围取为圆(以漂移轨迹端点为圆心，漂移误差率与风压左右漂移距离的乘积为半径)；随后做一个大圆，与左右2个小圆相切，并以一定的置信度扩充大圆，扩充之后的圆即为搜寻区域。

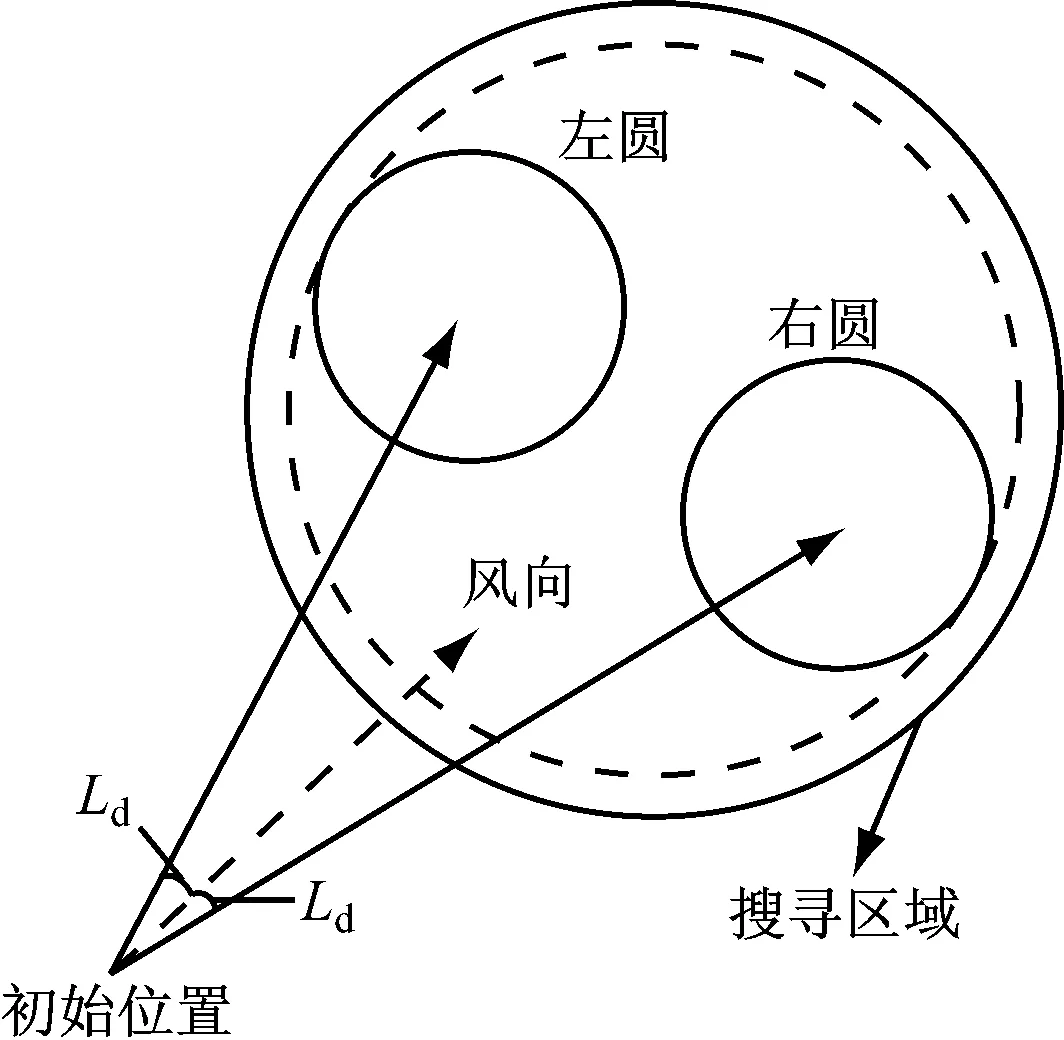
图3 解析法确定搜寻区域

解析法中，误差率和置信度主要根据经验选取，估计的搜寻区域因具体方法不同而形状各异。

3.2 Monte Carlo法

Monte Carlo法也称计算机随机模拟法，是以概率统计理论为指导的一类非常重要的数值计算方法。为了使用该方法估计搜寻区域，首先将目标看作单个粒子，在估计的事故位置附近生成大量服从某种概率分布的粒子，初始风压差在风向左右两侧的粒子数目各占1/2；随后用所建立的漂移模型对各个粒子的漂移轨迹进行预测，一段时间后所有粒子的凸包即为搜寻区域。

假设粒子的漂移满足马尔科夫过程，即目标未来位置的条件概率分布仅依赖于当前状态，与到达当前状态的历史路径无关。

P(xn+1|xn,xn-1,xn-2,…,x1)=P(xn+1|xn)

(17)

式(17)中：xi(i=1,2,3,…)为第i时刻目标的位置。

单个粒子的随机漂移过程可表示为

Δx=V0(n)ΔT+dε

(18)

xn+1=xn+Δx

(19)

式(18)和式(19)中：V0(n)为第n时刻目标的漂移速度；ΔT为离散时间步长；dε为具有零均值和已知方差的随机扰动项。

4 仿真试验与结果分析

采用MATLAB软件生成风速和流速数据以模拟实时风场和流场。在仿真试验中，速度单位为m/s，时间单位为s，假设遇难船事故位置坐标为(0,0)，仿真时间步长为600 s。定义x轴和y轴正向为东、北方向，x轴和y轴负向为西、南方向。

4.1 仿真对象

假设遇难船舶为渔船，根据文献[5]，其风压系数见表1。

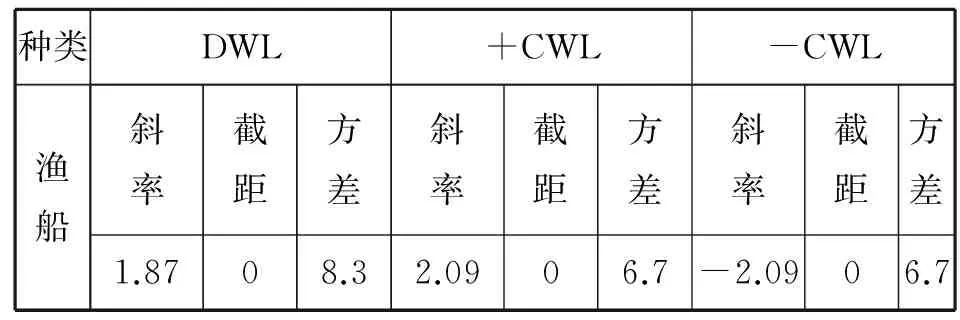
表1 船舶风压系数

4.2 漂移模型仿真

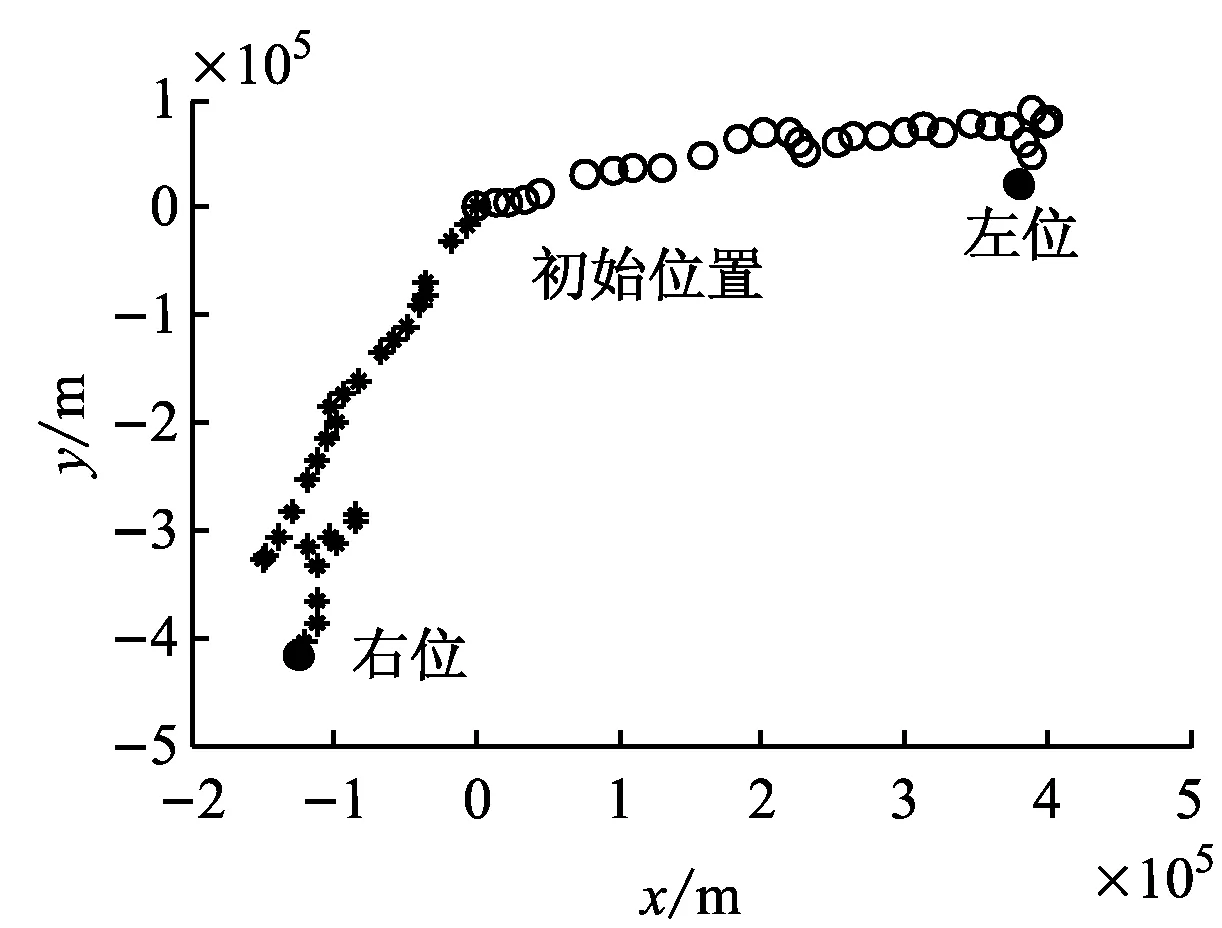
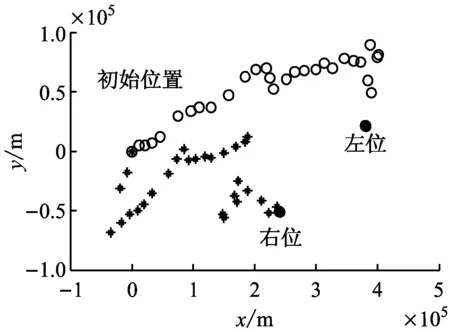
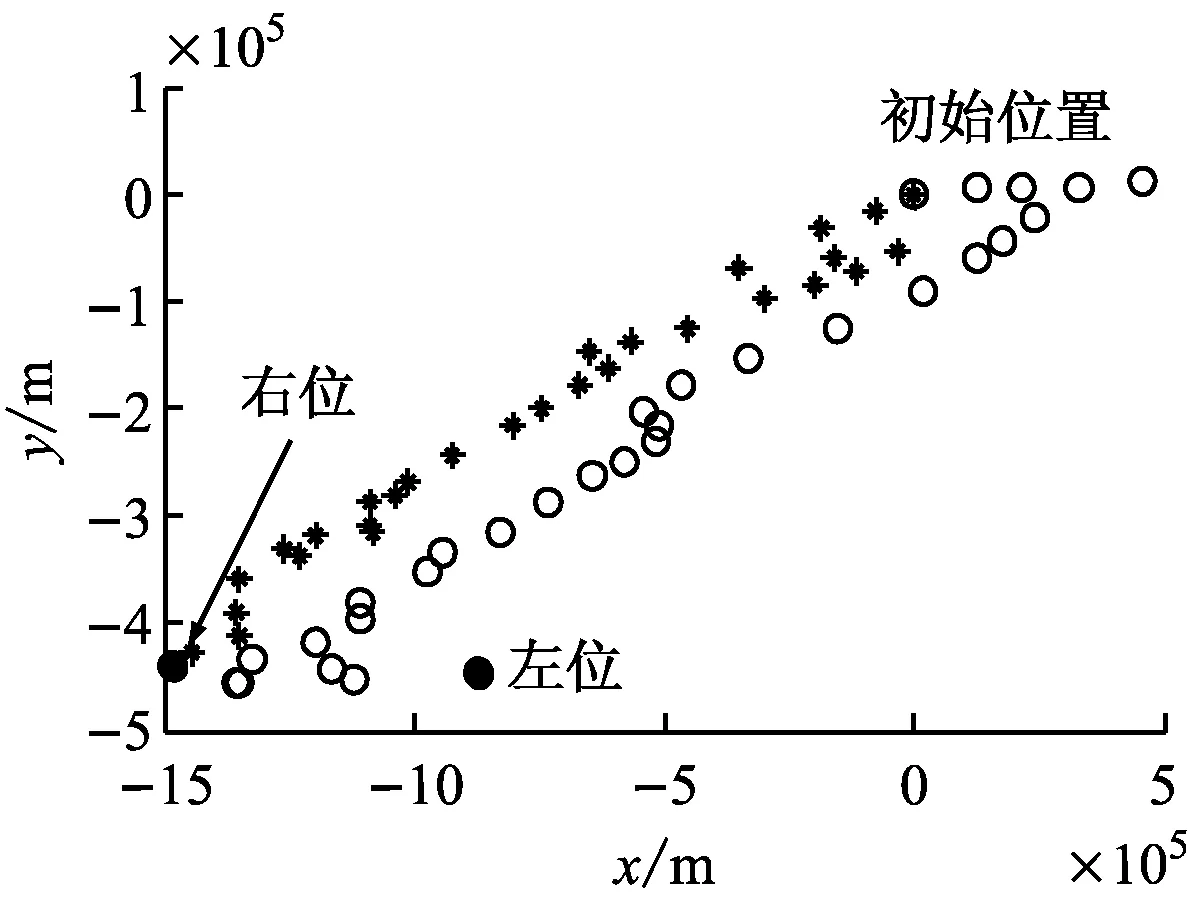
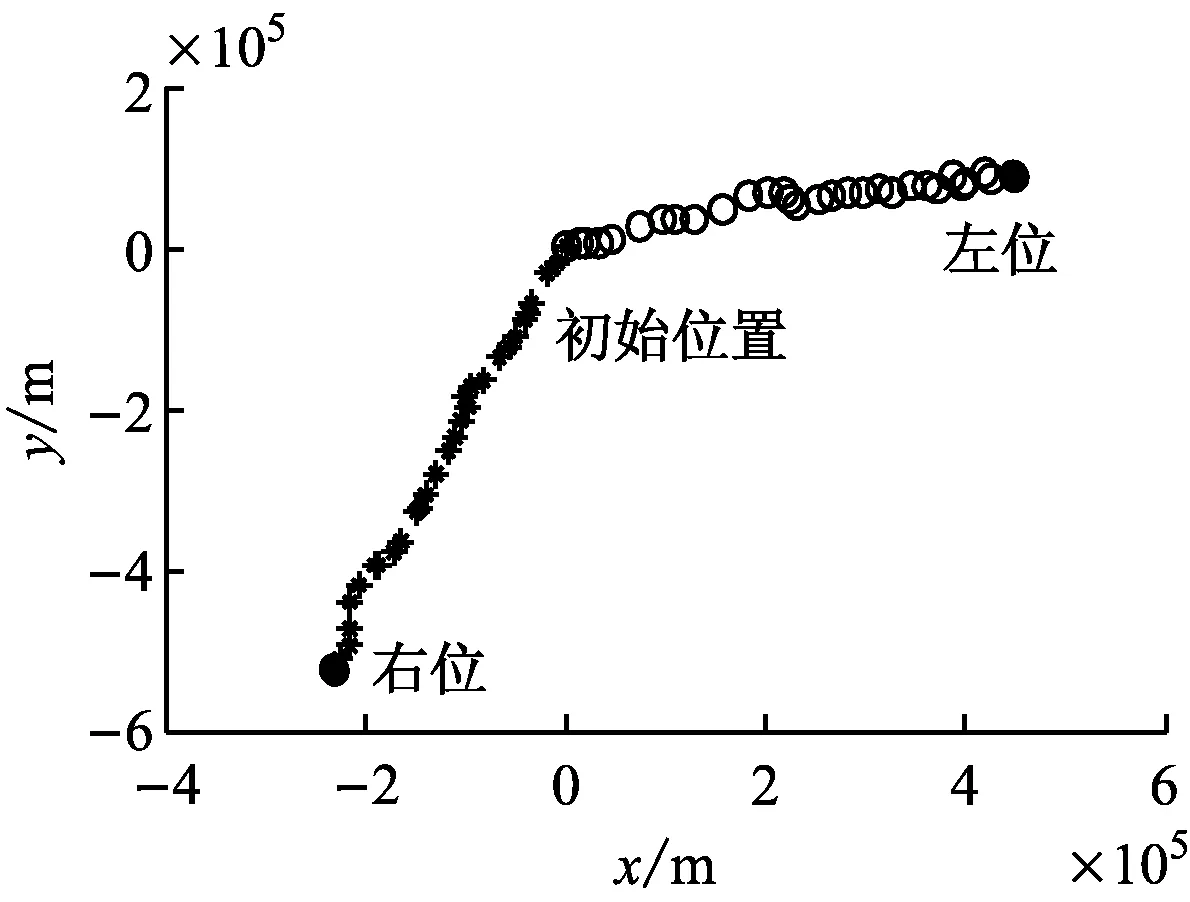
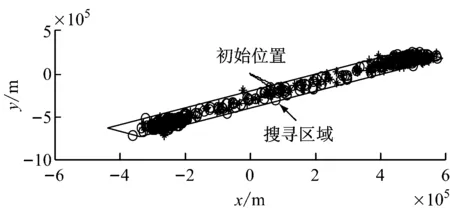
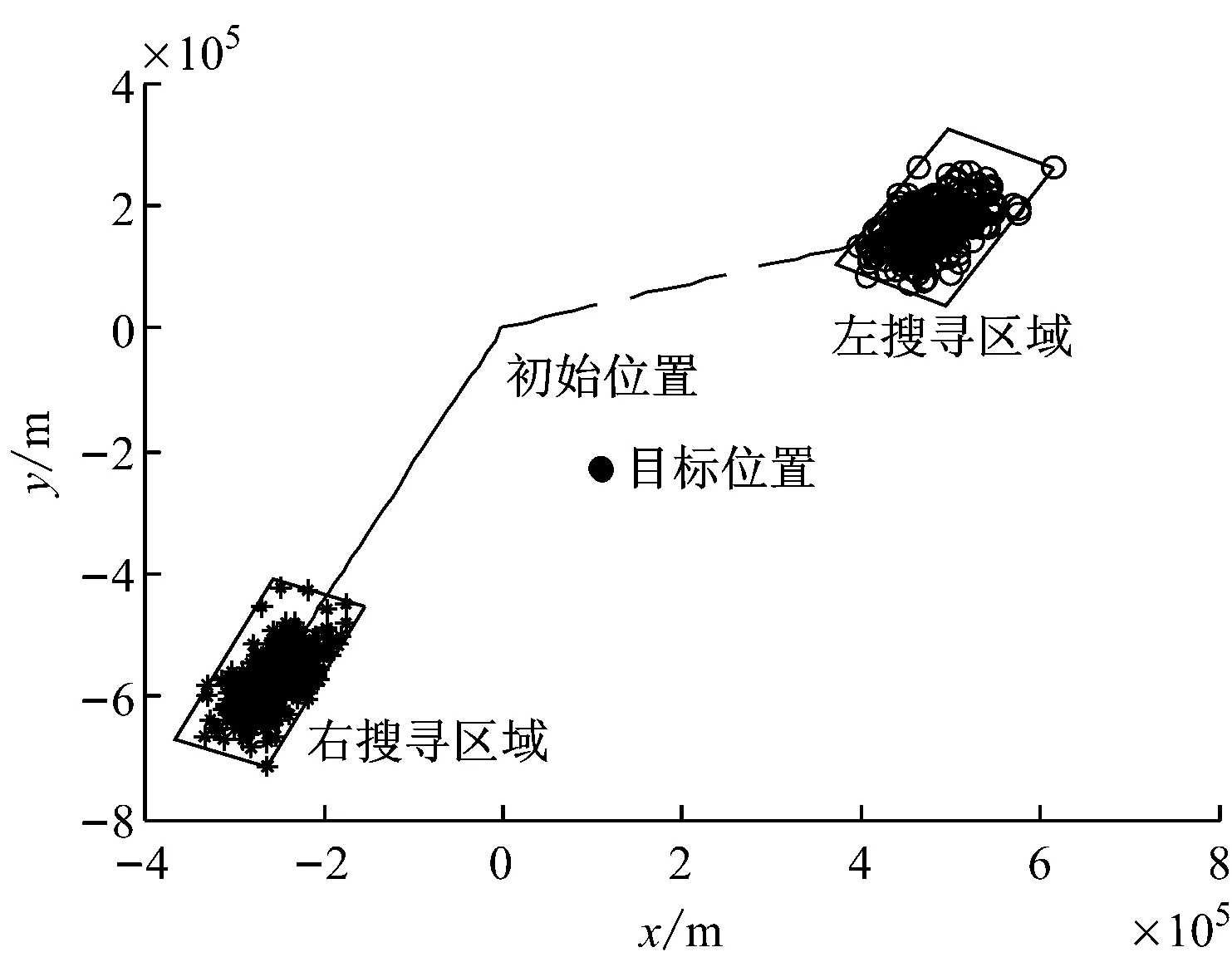
基于所建立的漂移模型，对遇难渔船的漂移轨迹进行预测。在风压差翻转率的计算式中，根据物体的质量越大其运动状态越难以改变的特性，目标漂移速度阈值与目标的质量呈负相关关系，且通常0

从仿真结果中可看出，考虑风压差翻转之后，粒子轨迹发生很大变化。粒子轨迹不再朝着一个方向前进，而是随着风压差方向的翻转而转向。风压差翻转的整体效果填充了图4f左右搜寻点间的位置空缺。比较图4b～图4d可看出漂移速度、风幅变化和风向变化对风压差翻转的影响各异；比较图4a和图4e可看出风速对风压差翻转的影响更大。风压差翻转的时刻和频率与a，β及r的取值有关。

4.3 估计搜寻区域

解析法估计的搜寻区域不仅包含最左和最右2个搜寻区域，还包括他们之间的区域。因此，解析法无需考虑风压差翻转。最左和最右风压差角取为±π/5，误差率取0.2，仿真结果见图5。

下面主要针对Monte Carlo法，在考虑风压差翻转和不考虑风压差翻转2种情况下进行仿真试验。在估计的事故位置(0,0)附近产生600个符合圆高斯分布的粒子，初始风压差在风向左、向右的粒子数目各占1/2。基于以上建立的漂移模型计算各个粒子的漂移轨迹，得到考虑风压差翻转和不考虑风压差翻转2种情况下的仿真结果(见图6)。

a)a=1，β=1，r=1

b)a=1.5，β=1，r=1

c)a=1，β=1.5，r=1

d)a=1，β=1，r=1.5

e)a=1，β=1.5，r=1.5

f)a=0，β=0，r=0

图5 解析法估计搜寻区域

从图6中可看出，考虑风压差翻转之后，左右2个搜寻区域不再孤立，两者之间的区域也成为搜寻区域。当实际发生风压差翻转而搜救计划者没有考虑时，很可能遗漏搜救目标，发生图7所示的情况，从而导致搜寻计划失败。因此，搜救计划者在制定搜寻计划时十分有必要考虑风压差翻转，尤其是在海洋环境恶劣时必须考虑。Monte Carlo法是一种随机模拟法，充分考虑漂移运动的不确定性，估计的搜寻区域小而精确，很大程度上提高了搜救的成功率。解析法本身不涉及风压差是否翻转，因此计算量小，而且估计的搜寻区域是连续的，不易遗漏搜救目标。但是，解析法中误差率和风压角参数很大程度上依赖于经验，估计的搜寻区域往往偏大，导致搜寻耗时长、搜寻代价高，而当海洋环境、目标漂移特型等不确定性非常大时可考虑使用。

a)考虑风压差翻转

b)不考虑风压差翻转

图7 估计搜寻区域失效

5 结束语

海上搜寻是海上搜救作业十分重要的部分，快速准确地确定包含搜救目标的最小搜寻区域对提高搜救成功率具有重要意义。针对风压差翻转问题提出风压差翻转率的计算方法，建立漂移模型，用于搜救目标漂移轨迹预测。在考虑风压差翻转时，比较解析法和Monte Carlo法估计搜寻区域的效果。通过仿真试验验证，结果表明：提出的风压差翻转率计算方法可提高漂移模型的精度，进而提高估计搜寻区域的可靠性；针对风压差翻转进行的研究工作对制订搜寻计划仍具有重要指导意义和参考价值。

[1] 刘海峥, 赵怀慈, 赵春阳. 基于Monte Carlo方法的搜救区域预测算法[J]. 船海工程, 2010, 39(1):132-135.

[2] BREIVIK Ø, ALLEN AA, MAISONDIEU C，et al. Advances in Search and Rescue at Sea[J].Ocean Dynamics, 2013, 63(1):83-88.

[3] BREIVIK Ø, ALLEN AA, MAISONDIEU C，et al. Wind-Induced Drift of Objects at Sea: The Leeway Field Method[J].Applied Ocean Research, 2011,33(2): 100-109.

[4] ISOBE A, HINATA H, KAKO S，et al. Interdisciplinary Studies on Environmental Chemistry Marine Environmen-tal Modeling and Analysis[M]. Tokyo: TERRAPUB, 2011：239-249.

[5] ALLEN A, LEEWAY D. USCG R & D Center Technical Report CG-D-05-05. [EB/OL]. (2015-08-11). http: // www. ntis.gov.

[6] NI Z, QIU Z P, SU T C. On Predicting Boat Drift for Search and Rescue[J].Ocean Engineering, 2010, 37(13): 1169-1179.

[7] WANG S Z, NIE H B, SHI C J. A Drifting Trajectory Prediction Model Based on Object Shape and Stochastic Motion Features[J].Journal of Hydrodynamics, Ser. B, 2014, 26(6):951-959.

[8] VANDENBULCKE L, BECKERS JM, LENARTZ F，et al. Super-Ensemble Techniques: Application to Surface Drift Prediction[J].Progress in Oceanography, 2009, 82(3): 149-167.

[9] BREIVIK Ø, ALLEN A A. An Operational Search and Rescue Model for the Norwegian Sea and the North Sea[J]. Journal of Marine Systems , 2011, 69(1-2):99-113.

[10] 夏宇亮. 基于云和场理论搜寻区域漂移粒子的密度表征[D]. 大连:大连海事大学,2010.

[11] HODGINS DO, HODGINS SLM. Phase Ⅱ Leeway Dynamics Program: Development and Verification of a Mathematical Drift Model for Life Rafts and Small Boats[R].Repot No.5741,Canadian Coast Guard,1998.

[12] SØRGARD E, VADA T. Observations and Modeling of Drifting Ships[R]. DNV Technical Report 96-2011, Detnorske Veritas, Høvik, Norway, 1998.

[13] 国际海事组织，国际民用航空组织.国际航空和海上搜寻救助手册修整案[M].中华人民共和国海事局，译.北京：人民交通出版社,2009.

Determination of Maritime Search Area Based on Leeway-Jibing Drift Model

(

ZHENGHongzhe1,2,3,ZHAOHuaici1,3,WANGLiyong1,31.ShenyangInstituteofAutomation,ChineseAcademyofSciences,Shenyang110016,China; 2.UniversityofChineseAcademyofScience,Beijing100049,China; 3.KeyLaboratoryofOptical-ElectronicsInformationProcessing,ChineseAcademyofSciences,Shenyang110016,China)

1000-4653(2016)04-0102-06

U676.8

A

2016-05-15

国家重点型号资助项目

郑宏喆(1990—)，女，河南新乡人，硕士，从事海上搜救研究。E-mail：lily19900323@163.com