基于优化灰色模型的柴油机状态分析及故障预测

， ，

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

基于优化灰色模型的柴油机状态分析及故障预测

韩冰，尹振杰，王岘昕

(上海船舶运输科学研究所航运技术与安全国家重点实验室，上海200135)

针对柴油机状态分析及故障预测问题，提出一种基于神经网络优化的灰色模型预测方法。在建立多维GM(1,5)模型的基础上，利用遗传算法优化的神经网络构建误差补偿器，进而构建GBPGA预测模型，实现对柴油机的状态分析及故障预测。以柴油机故障仿真试验数据为样本对该模型进行验证，结果表明构建的GBPGA预测模型能有效地对柴油机潜在的故障进行预测。

船舶工程;故障预测；神经网络；GM(1,5)；遗传算法；GBPGA

Abstract: Targeting the problem of status analysis and fault prediction for diesels, a new gray-system-based prediction model, optimized by neural network and genetic algorithm, is introduced. The neural network is employed for correcting the error that originates from gray prediction, and the GA is for further optimization. The combination of the three algorithms is named the model of GBPGA. The combined prediction model with preferable structure and parameters is applied to simulation and analysis of data of AVL boost. Experiment results show that the model is capable of predicting accurately, and is well used in fault prediction.

Keywords: ship engineering; fault prediction; neural network; GM(1,5); genetic algorithm; GBPGA

柴油机是船舶的核心设备，对其状态分析及故障预测技术进行研究对保障船舶安全运行具有重要意义。常用的柴油机状态分析方法[1]有域值分析、时间序列分析和频域分析等。对柴油机故障进行预报，建立具有较高精度的故障预测模型是近年来柴油机状态分析及故障预测技术研究的焦点。目前采用的柴油机状态预测模型[2]主要有时间序列预测模型、灰色预测模型及神经网络模型等,其中灰色预测模型通过对原始数据进行处理，利用数据间的关系建立灰色模型，发现、掌握系统的发展规律，对系统的未来状态作出预测[3]。文献[4]将灰色预测模型应用到柴油机故障状态分析中，为柴油机故障预测技术研究提供新的思路，然而其较弱的非线性逼近能力使得模型对非线性数据预测的效果不太理想。

神经网络具有较强的非线性函数逼近能力，将其与灰色模型相结合可弥补其非线性方面的不足。叶晓斌[5]构建针对飞行器故障的灰色神经网络预测模型；LI[6]将神经网络与优化的灰色模型相结合，分析组合预测模型的优势。将神经网络应用到灰色模型中已取得一定的成果，但受误差梯度算法的局限性影响，在学习训练时容易陷入局部最优，导致模型误差不稳定，多次的预测结果不尽相同。因此，可在神经网络的训练过程中引入优化机制，克服该弊端。

考虑到柴油机故障行为的非线性、多参数和“小样本”等特征，引入灰色预测模型，利用灰色模型“小样本”、分类精度高的特征分析评估柴油机的故障工况。同时，采用具有良好全局性和并行性优点的遗传算法优化神经网络，利用优化后的神经网络构建误差补偿器，对灰色预测进行误差补偿，建立GBPGA组合预测模型，进而实现对柴油机的状态分析及故障预测。

1 柴油机故障模型及样本数据提取

以TBD620L6柴油机为研究对象，通过引入AVL boost软件建立柴油机工况仿真模型；进一步模拟柴油机的工作状态及几种典型的故障形式，获取试验分析样本数据。

1.1 柴油机工况模型

依据TBD620L6柴油机的系统结构和试验性能参数(由制造厂家提供)，在AVL boost提供的模型编辑器中选取主要元件建立柴油机工况仿真模型，并按工作原理连接各元件及布置测量点。建立的TBD620L6柴油机工况仿真模型见图1。

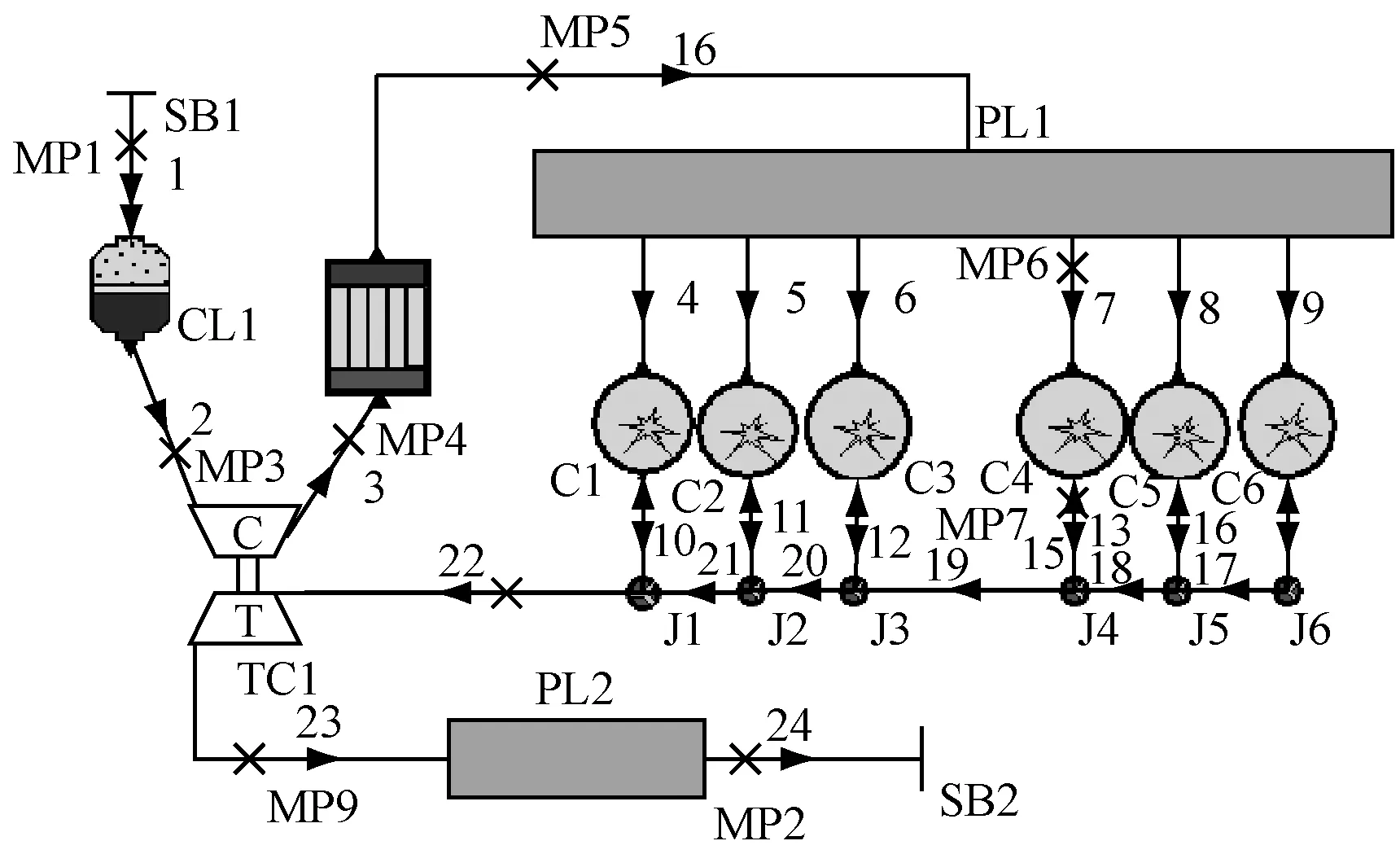
图1 TBD620L6型柴油机工况仿真模型

仿真模型包含气缸元件(C1～C6)、进气管(PL1)、排气管(PL2)、中冷器元件(CO1)、涡轮增压器元件(TC1)、空气过滤器(CL1)、系统边界(SB1～SB2)及连接管道(J1～J6)，并在测量的相应位置上布置9个测点(MP1～MP9)。

确定各元件的边界条件和初始条件，选取缸内的燃烧模式和热传导模型分别为单VIBE函数及Woschni1978模型，增压模型选择简化模式。[7]

1.2 性能参数的选取

结合柴油机故障诊断系统所需的热力性能参数，选取5组相关的热力性能参数作为测试诊断参数。通过对这5组诊断参数的状态和变化趋势进行分析，实现对气缸内工作过程的监测诊断。选取的5组监测诊断参数分别为：平均有效压力Pg(bar)、有效燃油消耗率ge(g/(kW·h))、爆发压力Pz(MPa)、最大压力升高比λmax及涡轮后排气温度Tout(K)。这其中，平均有效压力和爆发压力是衡量柴油机动力性能的主要指标，爆发压力又可判断各零部件所承受的负荷；有效燃油消耗率是衡量经济性能的重要指标；最大压力升高比可判断柴油机的燃烧程度；涡轮后排气温度可反映增压器的工作状态和各缸的排气温度及工作效率等。

1.3 样本数据

结合试验数据，在额定工况下对仿真模型进行试验标定。同时，选取在100%，75%，50%和25%负荷下测试柴油机的5组性能参数，将仿真数据与试验数据进行对比。结果表明，涡轮后排气温度的相对误差最大，为2.57%，其他各性能参数的相对误差都在5%以内，模型的精确度和可靠性得到验证。

通过调整仿真模型各元件的初始参数值，在额定工况下模拟柴油机的正常工作状态和5种典型故障形式(见表1),通过软件计算测量并记录各诊断参数值。整理记录的结果并建立基准故障向量表。按时间序列从特定的故障模式中选取多组诊断参数值作为初始向量，建立原始数据表。基准故障向量表见表2，空冷器效率故障原始数据表见表3。

表1 故障形式列表

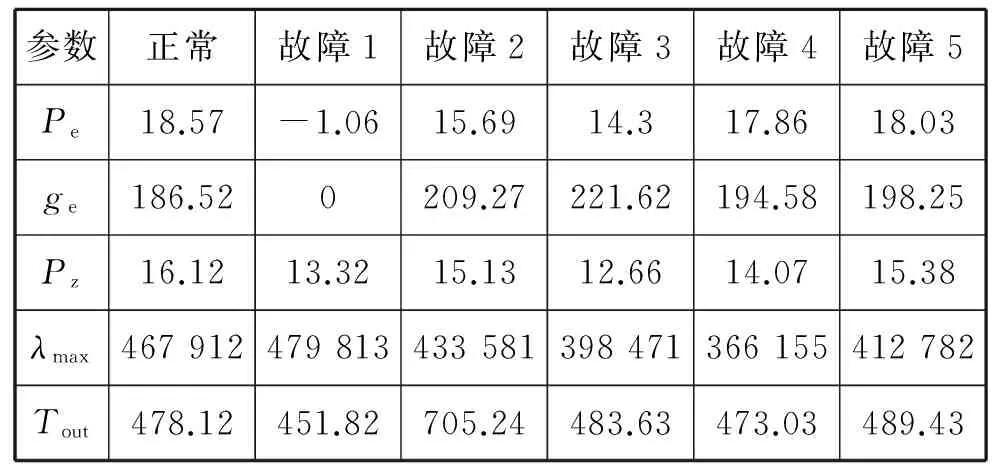
表2 基准故障向量表

2 动态组合预测模型的建立

结合所选的柴油机故诊断参数建立多维GM(1,5)模型作初步预测，得到初步预测值与预测误差；引入遗传算法对神经网络进行优化，得到网络最优权值与阈值；利用优化的BP神经网络构建误差补偿器，计算误差补偿值，进而对灰色模型的初步预测值进行修正，得到最终预测值。整个过程构成的模型称为GBPGA组合预测模型，最终预测值即为灰色模型的初步预测值与补偿误差值之和。

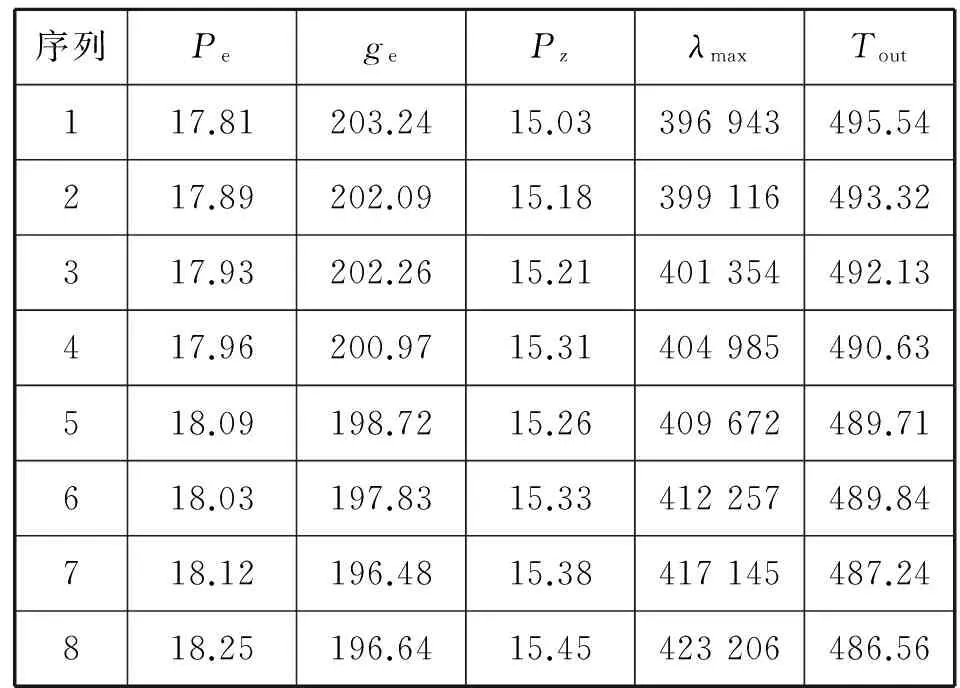
表3 空冷器效率故障原始数据表

2.1 确立GM(1,5)模型

灰色预测模型是对原始数列作一次累加生成之后利用累加数列建立灰色微分方程而形成的预测模型。整个过程可看作是样本数据随时间序列的发展，由灰色量或灰色过程逐步白化得到清晰的表现方式，建立相应于微分方程解的模型并作出预测。[8]通常采用一阶一维GM(1,1)进行灰色建模，结合柴油机故障行为的多参数特征建立一个多维灰色GM(1,5)预测模型，其中括号内的1和5分别表示方程的阶数及变量的维数。

根据灰色系统理论，建立离散化的时间序列预测模型[9]为

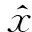
(1)

k=1,2,…

式(1)中：a为参数矩阵；u为灰作用矩阵；a和u的值取决于原始数据及其背景值。

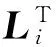
(2)

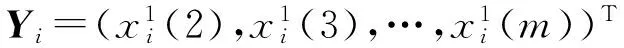
2.2 神经网络误差补偿器

神经网络误差补偿是利用神经网络建立拓扑结构，构建训练数据与误差间的映射关系，从而训练测试数据得到补偿误差，进而对初步预测值进行修正。

三层BP神经网络(即输入层、隐含层及输出层)具有很强的非线性函数逼近能力，因此选取三层网络结构构建误差补偿模型。各层节点数的选择取决于研究对象的复杂程度及经验公式。[10]结合柴油机故障仿真选取的特征参数，选取神经网络拓扑结构为5×6×5，即输入层和输出层均设置5个神经元，隐含层6个神经元。这其中：W=(wji)5×6为输入层与隐含层间的连接权矩阵；V=(vlj)6×5为隐含层与输出层间的连接权矩阵。

2.3 遗传算法优化神经网络

遗传算法具有全局性和并行性，为避免神经网络训练陷入局部最优，引入遗传算法对神经网络进行优化，获取网络的最优初始权值和阈值。其主要思路为：初步确定神经网络的结构，给出学习样本，由输入样本计算得到模型输出，根据模型输出计算其与期望值的误差，并以该误差作为个体适应度值进行优化。遗传算法具体优化步骤[11]如下。

2.3.1种群初始化

随机产生S个个体，S为种群数目。初始化种群的目的是获取良好的模型，使遗传算法模型在计算分类上更优于传统模型。

2.3.2计算适应度函数

适应度函数是遗传算法的核心，在全局信息搜索方面占据着不可替代的位置。因此，恰当地构建适应度函数是形成优良算法的重要环节。个体的适应度由适应度函数计算得到，其大小决定某个体被遗传到下一代的概率。由适应度函数得到第i个染色体的适应度为

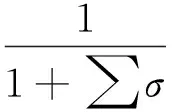
(3)

若误差σ满足需求精度或适应度f达到给定的最大值，则结束。

2.3.3选择操作

通过赌轮式选取的方式从上代中选择父体，交叉并得到2个子体。每个染色体被选择的概率pi=fi/∑fi。

2.3.4交叉操作

依据交叉概率的原则从群体中抽取2个染色体并进行交叉，可进一步提高遗传算法的搜索能力。交叉概率应在一定的范围之内，过小往往会导致搜索过程停滞不前，通常选取的范围为0.5～1.0。这里选取交叉概率pc=0.7。

2.3.5变异操作

为增强遗传算法的全局搜索能力、丰富群体的多样性，变异算子随机确定个体的基因位，进一步改变其基因值。若不存在变异，则不会有新的基因产生；若变异过大，则会使搜索过程趋近于随机搜索。变异概率的取值范围通常为0.01～0.20。这里选取变异概率pm=0.15。

2.3.6终止操作

循环操作，直到误差满足精度需求或适应度达到设定的最大值为止，获取神经网络的最优初始权值及阈值。

3 仿真分析

分别在MATLAB中进行灰色模型计算、神经网络优化和神经网络误差补偿，对提出的预测方法进行试验验证。通过仿真计算得到GBPGA模型的预测结果，并将其与灰色模型、神经网络模型的预测结果进行对比，验证模型的精度。最后，通过灰色关联分析，进一步判断柴油机的故障状态。

模型的建立过程为：累加前7组初始数据建立灰色微分方程，建立多维新陈代谢GM(1,5)模型，作初步预测，得到初步预测值和误差值；利用遗传算法优化BP神经网络，通过网络训练使误差函数达到最小，确定网络最优权值和阈值；利用优化后的神经网络构建误差补偿器计算补偿误差，将前7组初始数据的预测值作为网络输入，相应的7组误差值作为网络的期望输出，训练网络，使误差函数达到最小；训练第8组预测数据得到补偿误差，最终预测值即为初步预测值与补偿误差值之和。

3.1 模型仿真结果

遗传算法优化过程中的最优个体适应度值见图2，优化后的神经网络训练误差收敛曲线见图3。由图2和图3可知：利用遗传算法优化得到的最优适应度值为0.018 6；神经网络训练实际误差为9.979 19×10-5，经过1 569次迭代网络收敛得到第8组的误差补偿值为[0.24 3.01 0.28 8 710 8.03]，不同模型的最终预测值及误差比较见表4。

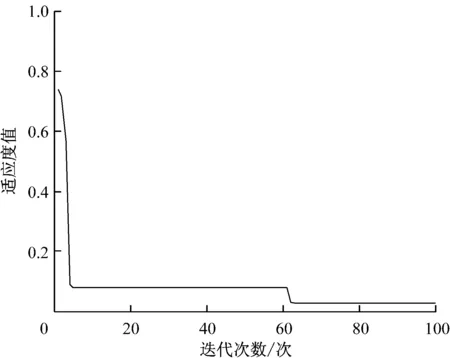
图2 最优个体适应度值

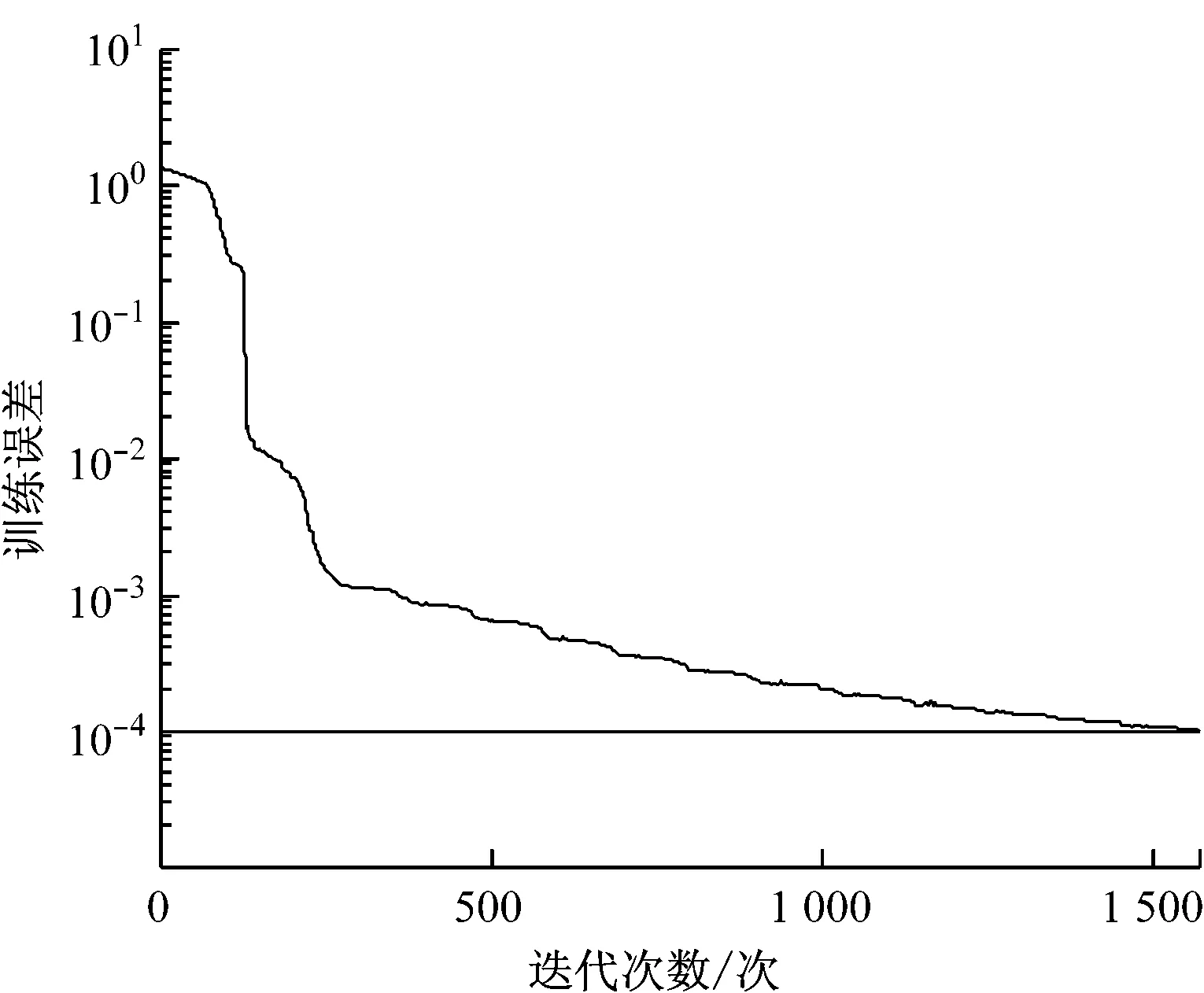
图3 优化后的神经网络训练误差收敛曲线

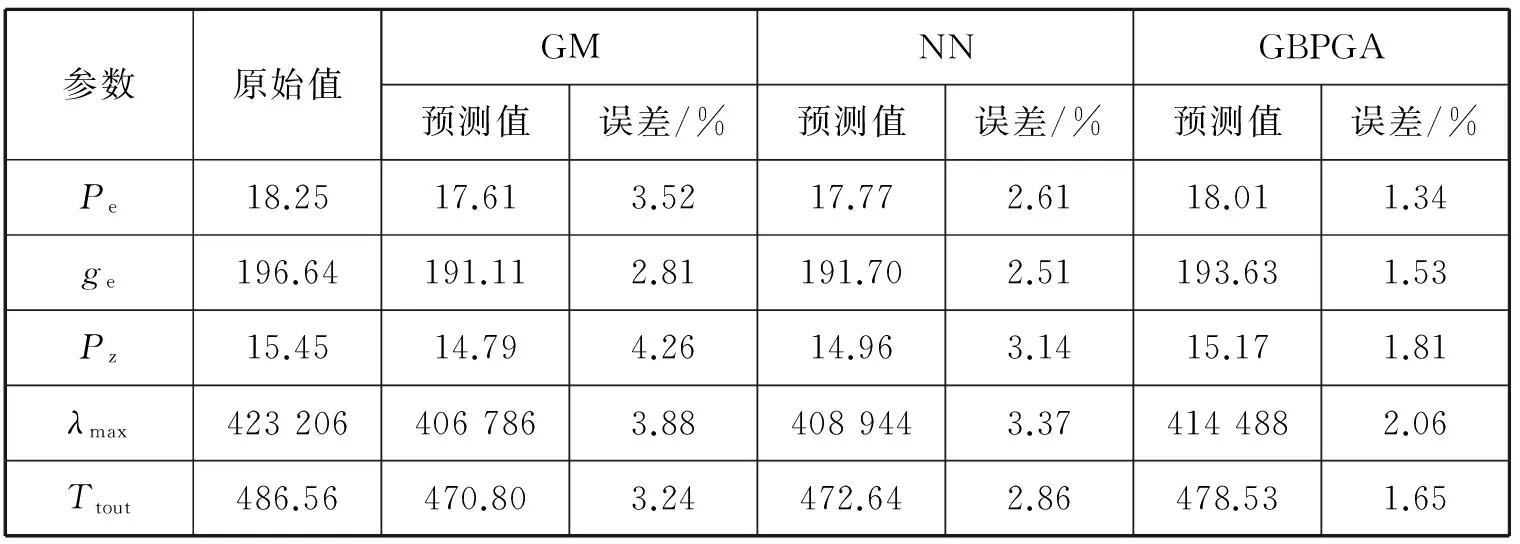
参数原始值GMNNGBPGA预测值误差/%预测值误差/%预测值误差/%Pe18.2517.613.5217.772.6118.011.34ge196.64191.112.81191.702.51193.631.53Pz15.4514.794.2614.963.1415.171.81λmax4232064067863.884089443.374144882.06Ttout486.56470.803.24472.642.86478.531.65

结果表明，采用GBPGA预测模型得到的预测结果的精度要比单灰色预测和单神经网络模型的预测结果高。分析其原因，主要是由于遗传算法对网络权值和阈值进行了优化，优化后的误差补偿对预测值有一个校正和优化，提高了模型的预测精度。

3.2 状态预测及故障诊断

依据灰色关联分析方法计算各组检测向量与所有基准故障向量之间的灰关联度，得到灰色关联度矩阵。灰色关联度矩阵中每一行表示一种故障模式，每一列表示一种检测向量。依据最大灰色关联度判断准则[12]进行故障判断：在灰色关联度矩阵的每一行中，灰色关联度最大的值所对应的状态即为改组检测向量对应的故障模式。

计算GBPGA模型的预测数据与基准故障向量之间的关联度，为更清楚地表达灰色关联度矩阵的含义，将矩阵以列表的形式表示为

M1=[0.827 3 0.677 9 0.765 4 0.679 7 0.807 7 0.931 9]

(1)

式(1)中：第1列关联度对应的柴油机工况为正常工作；第2～6列关联度对应的柴油机工况分别为故障1～故障5。

由此可得，GBPGA模型的预测数据产生的最大灰色关联度为矩阵最后一列，表明采用GBPGA模型的预测结果为故障5，即柴油机处于空冷器效率故障，与原仿真模型的故障模式一致。因此，GBPGA模型的预测结果可准确描述柴油机在第8时刻的故障形式，即该模型可准确预测柴油机的工作状态。

同理，再从原正常工作仿真模型中选取特征参数建立原始数据表，按上述方法采用GBPGA模型进行数据预测，并进一步判断柴油机的工作状态。正常工作模型原始数据见表5。

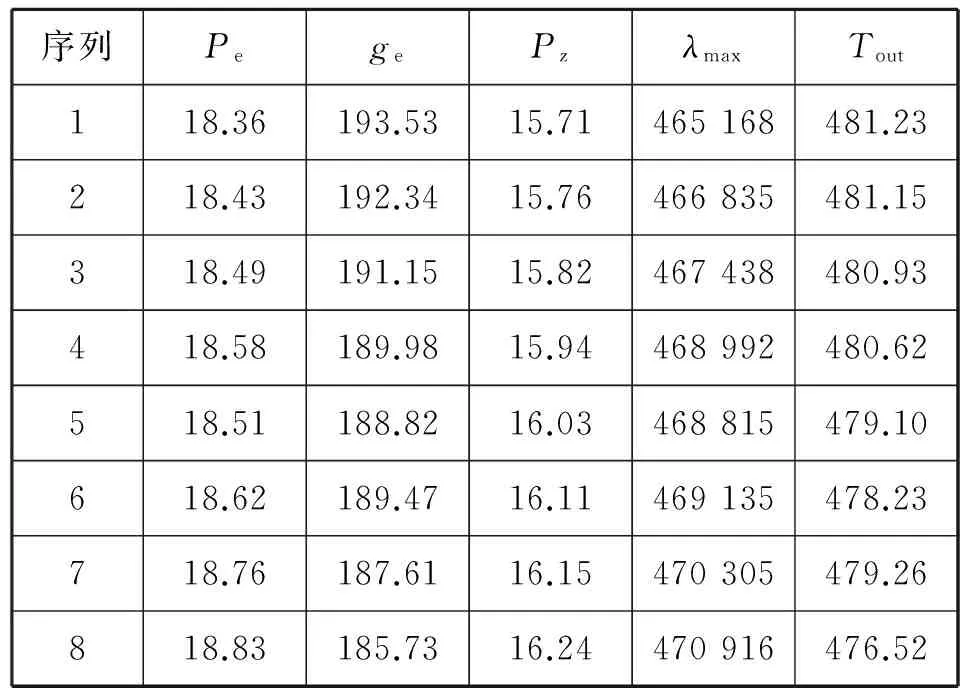
表5 正常工作模型原始数据

利用GBPGA模型对表5中的数据进行预测，得到的预测值为[18.58 182.89 15.95 461.00 215.00 468.66]。通过灰色关联分析对预测值所对应的工作状态进行判断，得到灰色关联度矩阵为M2=[0.980 2 0.780 6 0.745 1 0.631 0 0.714 30.794 4]。

由此得到模型预测结果，工作状态判断为正常工作，与原仿真模型一致。因此，该预测模型能有效地预测出柴油机的工作状态及故障形式。

4 结束语

在灰色模型的基础上引入遗传算法对神经网络进行优化，并进一步构建神经网络误差补偿器对灰色模型的预测值进行误差补偿，进而提出GBPGA动态组合预测模型。试验结果表明，GBPGA动态组合预测模型预测结果可靠、准确度高，能有效判断出柴油机的故障形式。此外，针对不同时间序列的柴油机状态参数评估与趋势预测有待进一步研究。

[1] 郭江华, 侯馨光，陈国钧，等. 船舶柴油机故障诊断技术研究[J]. 中国航海, 2005(4)：75-78.

[2] 闫显. 船用柴油机智能故障预测技术研究[D]. 镇江： 江苏科技大学, 2011.

[3] 刘思峰, 谢乃明. 灰色系统理论及其应用[M]. 北京：科学出版社, 2008：11-15.

[4] 于涛. 基于灰色系统理论的柴油机故障诊断方法研究[D]. 哈尔滨：哈尔滨工程大学, 2012.

[5] 叶晓斌.基于灰色系统理论和神经网络的机械故障预测模型及其应用[D].重庆:重庆大学,2012.

[6] LI X Y. Optimized Grey RBF Prediction Model Based on Genetic Algorithm[C].CSSE， 2008： 74-77.

[7] 潘光艳. 620单缸机结构设计、性能分析以及主要运动件有限元计算[D]. 哈尔滨： 哈尔滨工程大学，2008.

[8] 袁景凌,李小燕,钟珞.遗传优化的灰色神经网络模型比较研究[J].计算机工程与应用,2010:41-43.

[9] 李国勇，闫芳，郭晓峰. 基于遗传算法的灰色神经网络优化算法[J]. 控制工程, 2013，20(5)：934-937.

[10] 许丽君, 陈红卫. 神经网络在船舶柴油机故障诊断中的应用研究[J]. 计算机测量与控制, 2013,21(6):50-52.

[11] 周明, 孙树栋. 遗传算法原理及应用[M]. 北京：国防工业出版社, 1999:25-31.

[12] 苟军, 熊静琪. 灰色关联度在柴油机故障诊断中的应用与改进[J]. 车用发动机, 2007(1):72-75.

Fault Prediction of Diesel Engine Based on Optimized Grey Model

HANBing,YINZhenjie,WANGXianxin

(State Key Laboratory of Navigation and Safety Technology, Shanghai Ship and Shipping Research Institute, Shanghai 200135, China)

1000-4653(2016)04-0038-05

U664.121

A

2016-08-22

上海市青年科技启明星计划资助项目(15QB1400800)

韩 冰(1981—)，男，吉林省吉林市人，副研究员，从事船舶动力装置及动力定位研究。E-mail: hanbing@sssri.com 尹振杰(1988—)，男，河北邯郸人，硕士，从事舰船动力装置故障诊断与预测研究。E-mail: vin2009@126.com