分段组合Kalman滤波在滚转弹SINS/GPS系统中的应用研究

刘可可,马国梁,李元生

(1.南京理工大学 能源与动力工程学院,南京 210094;2.中国船舶工业系统工程研究院,北京 100094)



分段组合Kalman滤波在滚转弹SINS/GPS系统中的应用研究

刘可可1,马国梁1,李元生2

(1.南京理工大学 能源与动力工程学院,南京 210094;2.中国船舶工业系统工程研究院,北京 100094)

为解决滚转弹SINS/GPS系统的运动参数估计问题,建立了广义误差模型,采用输出校正滤波对测量误差进行估计,进一步将输出校正滤波和反馈校正滤波进行了分段组合,给出了输出校正和反馈校正滤波原理图和分段组合流程图。根据SINS/GPS组合系统松组合模型,以某滚转弹六自由度仿真数据为例进行仿真。仿真结果表明,文中提出的分段组合Kalman滤波方法提高了估计精度。研究结果可为精确测量滚转弹的运动参数问题提供有效的解决办法。

滚转弹;运动参数;Kalman滤波;输出校正;反馈校正

低成本的远程精确打击技术是目前弹箭技术的重点发展方向之一。运动参数的测量是弹箭气动布局、弹道参数及特性研究的基础。由于发射过程处于高过载、高动态条件下,获取准确的运动参数十分困难[1-3],而单个测量系统亦不能满足所需,因此有必要探讨研究组合测量系统。捷联惯性导航系统(SINS)不受外界干扰的影响,隐蔽性好,并且数据更新率高、短期精度和稳定性好,但导航信息是经过积分得到的,其定位误差会随时间的推移而增大,长期精度较差。全球定位系统(GPS)可以连续、精确地提供三维位置信息和速度信息,并且不随时间发散,长期稳定性好。但是,当GPS载体作高动态运动时,接收机极易受到干扰,导致卫星信号暂时丢失,使定位无法进行。由此可看出SINS和GPS的组合不是简单相加,而是具有优势互补,扬长避短的特点。在SINS/GPS组合系统中,可以采用一种低性能的惯性导航系统,利用惯导系统的速度信号解决动态跟踪问题,而高精度定位则由GPS来实现,这样大大降低了成本,因此它们的组合系统成为近年来导航领域的热点[4-6]。它们的组合模式有3种,分别是松组合、紧组合和深组合。但应用时采用松组合较多,以往的这种组合主要用在飞机导弹上,应用在滚转弹上并不常见。

组合导航系统的运动参数估计主要采用的是Kalman滤波器[7],由于本文研究的滚转弹具有高动态、高过载等特性,这就给单一的输出校正滤波和反馈校正滤波算法带来了较大的难度。为此本文提出了一种基于输出校正和反馈校正的分段组合Kalman滤波方法。仿真结果表明,采用分段组合Kalman滤波不仅能使运动参数的估计精度提高,同时可以达到较好的收敛效果。

1　误差状态方程的建立

在实际应用中,导航系统开始工作前传入的数据都存在误差,并且在SINS/GPS组合系统中,捷联惯性导航系统作为主系统,其误差方程被作为Kalman滤波的状态方程。因此,建立惯性导航系统的误差方程意义重大。

1)姿态误差方程。

(1)

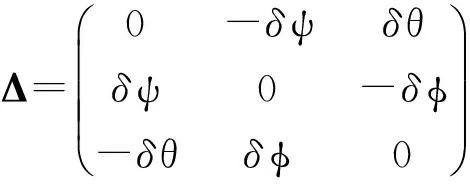
将式(1)整理后,可得:

(2)

该方程微分后,得到误差方程:

(3)

(4)

(5)

将式(1)、式(4)、式(5)代入式(3),整理后得:

(6)

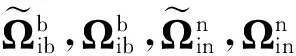
(7)

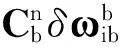
(8)

(9)

式(9)即为姿态角误差方程。

2)速度误差方程。

在导航坐标系下[8],速度计算方程为

(10)

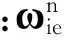
对式(10)微分即可得速度的误差方程:

δvn+δgn

(11)

故

于是式(11)可化为

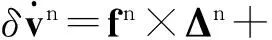
(12)

纬度L、经度l和距地表的高度h计算公式如下[9]:

(13)

式中:vN,vE,vD分别为北向、东向、地向速度;RM为地球子午面曲率半径;RN为地球卯酉面曲率半径。RM,RN表达式如下:

在WGS-84中,R为地球长半轴,R=6 378 137.0m;e为地球椭球偏心率,e=0.081 819 190 842 6。式(13)的误差方程为

(14)

综上所述,误差状态方程可写为

(15)

X(t)=(φNφEφDδvNδvEδvDδLδlδhεgxεgyεgzaxayaz)T,其中,下标N,E,D分别表示北、东、地地理坐标系的3个方向；φN,φE,φD为INS平台误差角;δvN,δvE,δvD分别为北、东、地速度误差;δL,δl,δh为位置误差;εgx,εgy,εgz为陀螺仪的固定偏差;ax,ay,az为加速度计的固定偏差。W(t)=(WgxWgyWgzWaxWayWaz)T为系统过程测量噪声矢量,其中,Wgx,Wgy,Wgz为陀螺的测量噪声;Wax,Way,Waz为加速度计的测量噪声;F(t)为系统状态矩阵,G(t)为系统噪声传播矩阵。

矩阵F(t)具有如下的形式:

式中:FN是对应9个基本导航参数的矩阵,由捷联惯导基本误差方程决定,其非零元素如下：

由图5可以看出，随着氨水浓度的增加，磁性产品的产率也逐步增加(即赤铁矿的回收率逐步增加)。当氨水浓度达到1.0 mol/L时，赤铁矿回收率达到最大值。为此采用1.0 mol/L氨水浓度进行以下试验。

F(9,6)=-1,

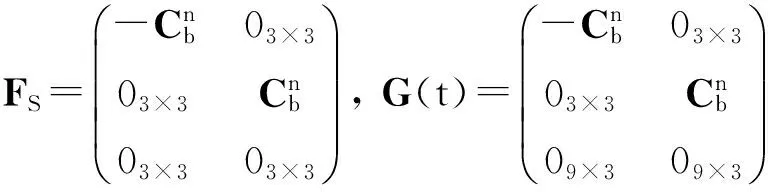
式中:Ω为地球自转角速率,在WGS-84中,Ω=7.292 115×10-5rad/s。

2　基于输出校正滤波的估计方法

2.1卡尔曼滤波基本原理

实际上,输出校正滤波和反馈校正滤波都是在卡尔曼滤波的基础上延伸得到的。卡尔曼滤波算法是一个高效的最优化自回归数据处理算法,它实质上是通过系统的量测信息重新构造系统的状态向量,并以“预测—实测—修正”的模式顺序递推,即利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计,求出现时刻的估计值。它主要包含2个信息更新过程:时间更新过程和量测更新过程[7]。具体计算可通过以下步骤来实现。

①状态一步预测。

Xk/k-1=Φk,k-1Xk-1

(16)

②均方差一步预测。

(17)

③滤波增益。

(18)

④状态估计。

Xk=Xk/k-1+Kk(Zk-HkXk/k-1)

(19)

⑤均方差误差估计。

(20)

式中:Φ为式(16)对应的离散状态转移矩阵;Qk为系统噪声Wk的协方差阵,为非负定阵;Rk为量测噪声Vk的协方差阵,为正定阵。

2.2输出校正滤波的实现

图1为INS/GPS组合输出校正的滤波示意图。

图1　INS/GPS组合输出校正的滤波示意图

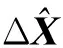
Z(t)6×1=H(t)6×15X(t)15×1+V(t)6×1

(21)

式中:

式中:Z(t)主要是由SINS和GPS的位置、速度的误差量组成;H(t)是量测值矩阵;V(t)是量测噪声;L,h分别表示纬度、高度;LI,hI和LG,hG分别表示INS和GPS所输出的纬度和高度;NE,NN,ND为GPS接收机沿东、北、地方向的距离测量误差;vIN,vIE,vID分别为INS输出的北向速度、东向速度和地向速度;vGN,vGE,vGD分别为GPS接收机直接输出的运载体的北向速度、东向速度和地向速度。

3　基于分段组合Kalman滤波校正方法

INS/GPS组合常采用的是输出校正,但用在滚转弹上却不能达到满意的效果。另一种方式是采用反馈校正滤波,其原理如图2所示[10]。

图2　SINS/GPS组合反馈校正的滤波示意图

同样,由图1输出校正滤波原理可知,若单纯用输出校正滤波,当上一时刻的估值误差较大,而此刻又以上一时刻为基准,这样误差会越来越大。由于弹丸的转速很高,初始误差较大,所以不能不考虑弹丸的特殊性。同时考虑到惯性导航系统本身就有随时间积累而发散的特点,因此单纯的输出校正滤波算法的收敛性亦难以保证。

由于以上2种滤波方法都不能达到较好的效果,因此考虑是否可以同时运用输出校正滤波和反馈校正滤波,结合二者的优点以提高滚转弹运动参数的测量精度。基于以上思路,本文提出了一种分段切换Kalman滤波算法,考虑到弹箭飞行过程中姿态参数的测量是其他运动参数测量的基础,因此切换条件就设定为姿态角,当姿态角的误差值小于1°时用反馈校正滤波,否则切换为输出校正滤波。其流程图如图3所示。

图3　输出反馈分段组合流程图

4　仿真分析

根据前面给出的SINS/GPS组合系统松组合模型,以某滚转弹六自由度弹道仿真数据为例,射向90°,即东向射击,射角30°。用卡尔曼滤波算法对系统进行仿真,地球相关常数定义均以WGS-84模型为基准。由上面的Kalman滤波核心方程式(16)～式(19)可以看出,仿真前需提供X(0)和P(0/0)的初始值。由于随着滤波步数的增加,任意选定的初始值对滤波值的影响会逐渐减弱直至消失,所以本文初值设定如下:X(0)初始值为0,初始方程阵P(0/0)取为对角阵,其对角线上的元素为

P1,1=(0.1°)2,P2,2=(0.1°)2,P3,3=(0.1°)2,

P4,4=(0.1)2,P5,5=(0.1)2,

P6,6=(0.1)2,P7,7=(10)2,P8,8=(10)2,

P9,9=(20)2,P10,10=(0.1°)2,

P11,11=(0.05°)2,P12,12=(0.05°)2,P13,13=

(0.1)2,P14,14=(0.05)2,P15,15=(0.05)2。

观测噪声方差阵设定对角阵,其元素为

R1,1=(0.1)2,R2,2=(0.1)2,R3,3=(0.1)2,

R4,4=(5)2,R5,5=(5)2,R6,6=(5)2。

过程噪声方差阵对角线上的元素设为

Q1,1=(0.1°)2,Q2,2=(0.1°)2,Q3,3=(0.1°)2,

Q4,4=(0.1)2,Q5,5=(0.05)2,Q6,6=(0.05)2。

图4～图6给出了输出校正滤波算法和切换Kalman滤波算法的仿真对比结果。图中,δθ,δψ,δφ分别为俯仰角误差、偏航角误差、滚转角误差；δvE,δvN,δvD分别为东、北、地速度误差；δL，δl,δh分别为纬度、经度和高度误差。

由于弹丸的转速很高,所以各参数的初始误差均较大,但随着时间的推移,经过滤波器的融合,误差将渐渐地减少。从图4(a)看出,输出校正滤波得到的俯仰角和偏航角的误差值一直在0上下浮动,不能收敛至0,其收敛效果不是很好。图4(b)是切换Kalman滤波姿态角误差曲线,从图中可以看出,俯仰角和偏航角的误差在20 s时基本都收敛到0,而滚转角误差的收敛速度则更快,在5 s左右就收敛为0。这表明切换Kalman滤波算法的收敛速度要明显快于输出校正滤波。

图5为速度误差曲线图,从图中可看出,2种算法的北向速度和东向速度误差区别较小,但地向速度误差则有明显的不同,输出校正滤波的最大误差为20 m/s,而切换Kalman滤波的最大误差则为10 m/s,其效果明显好于输出校正滤波算法。图6为位置误差曲线,从图6(a)可以明显地看出,输出校正滤波算法得到的经度和高度都随着时间在发散,而从图6(b)可以看出,切换Kalman滤波算法能获得很好的收敛效果。从以上的仿真结果可以明显看出,切换Kalman滤波算法具有更快的收敛速度和计算精度,其效果要明显好于单纯的输出校正滤波算法。

图4　输出校正和切换Kalman滤波姿态角仿真对比图

图5　输出校正和切换Kalman滤波速度仿真对比图

图6　输出校正和切换Kalman滤波位置仿真对比图

5　结束语

本文以滚转弹为研究对象,建立了SINS/GPS组合系统的松组合模型、卡尔曼滤波的状态方程和量测方程;分析了卡尔曼滤波的工作原理,并给出了输出校正和反馈校正滤波原理图及其使用范围。分析比较表明,单独使用反馈校正会失去稳定性,单独使用输出校正滤波收敛效果却不能满足需要。因此,本文基于分段滤波的组合导航思想,提出了一种切换Kalman滤波算法。仿真结果表明,切换Kalman滤波算法比单纯的输出校正滤波算法具有更快的收敛速度和更高的计算精度,具有一定的理论参考和工程应用价值。

[1]马国梁.高转速弹丸磁强计/太阳方位角传感器组合测姿方法[J].南京理工大学学报(自然科学版),2013,37(1):140-144.

MAGou-liang.Magnetometer/yawsondeintegratedattitudemeasurementforhighspinrateprojectiles[J].JournalofNanjingUniversityofScienceandTechnology(NaturalScience),2013,37(1):140-144.(inChinese)

[2]史金光,韩艳,刘世平,等.制导炮弹飞行姿态角的一种组合测量方法[J].弹道学报,2011,23(3):38-41.

SHIJin-guang,HANYan,LIUShi-ping,etal.Anapproachofcombinationmeasurementforflightattitudeanglesofguidedprojectile[J].JournalofBallistics,2011,23(3):38-41.(inChinese)

[3]DAVIDE,GAYLORE,GLENNL.GPS/INSKalmanfilterdesignforspacecraftoperationintheproximityoftheinternationalspacestation[C]//AIAAGuidance,Navigation,andControlConferenceandExhibit.Ausin,Texas:AIAA,2003.

[4]PARKDB,SHINDH.DevelopmentofaGPS/INSsystemforprecisionGPSguidedbombs[J].AerospaceandElectnricSystemsMagaiche,IEEE,2012,27(3):31-39.

[5]WANGLi-jun,ZHAOHui-chang,YANGXiao-niu.ThemodelingandsimulationforGPS/INSintegratednavigationsystem[J].IEEEConfencePublications,2008,4:1 991-1 994.

[6]GROSSJ,GUY,GURURAJANS.AcomparisonofextendedKalmanfilter,sigma-pointKalmanfilter,andparticlefilterinGPS/INSsensorfusion[C]//AIAAGuidance,Navigation,andControlConference.Toronto,Ontario,Canada:AIAA,2010.

[7]秦永元,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2012.

QINYong-yuan,WANGShu-hua.Kalmanfilterwithintegratednavigationprinciple[M].Xi’an:NorthwesternPolytechnicalUniversityPress,2012.(inChinese)

[8]张天光,王秀萍,王丽霞,等.捷联惯性导航技术[M].北京:国防工业出版社,2010.

ZHANGTian-guang,WANGXiu-ping,WANGLi-xia,etal.Strapdowninertialnavigationtechnology[M].Beijing:NationalDefenseIndustryPress,2010.(inChinese)

[9]杜习奇.GPS与捷联惯导组合导航系统研究[D].南京:南京理工大学,2004.

DUXi-qi.SINScombinedwithGPSnavigationsystem[D].Nanjing:NanjingUniversityofScienceandTechnology,2004.(inChinese)

[10]以光衢.惯性导航原理[M].北京:航空工业出版社,1987.

YIGuang-qu.Inertialnavigationprinciple[M].Benjing:AviationIndustryPress,1987.(inChinese)

[11]SHENXiang,ZHANGYong-jun,LUXiao.AnimprovedmethodfortransformingGPS/INSattitudetonationalmapprojcetionframe[J].GeoscienceandRemoteSensingLetters,IEEE,2015,12(6):1302-306.

Research on Piecewise Integrated Kalman Filter in SINS/GPS System of Spinning Projectile

LIU Ke-ke1,MA Guo-liang1,LI Yuan-sheng2

(1.School of Power and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China;2.Systems Engineering Research Institute,CSSC,Beijing 100094,China)

To solve the parameter estimation of spinning projectile SINS/GPS system,a generalized error model was established.The output correction filter was utilized to estimate the errors of measurement,and then a new filter was proposed by piecewise integrating the output correction filter with the feedback correction filter.Schematic diagrams of the output correction filter and the feedback correction filter,and the flow chart of the piecewise-integrated filter were also provided.According to the loose integrated model of SINS/GPS system,the simulation was carried out by taking the 6DOF simulation data of certain spinning projectile for instance.The numerical simulation results show that the proposed piecewise-integrated Kalman filter can improve the estimation accuracy.The results can provide an effective solution to accurately measuring the motion parameters of the spinning projectile.

spinning projectile;motion parameters;Kalman filter;output correction;feedback correction

2015-05-13

刘可可(1987- ),女,硕士研究生,研究方向为飞行器导航、制导与控制。E-mail:1418839092@qq.com。

通过作者:马国梁(1976- ),男,副教授,研究方向为飞行器导航、制导与控制。E-mail:mgljob@163.com。

TJ765.1

A

1004-499X(2016)01-0045-07