基于遗传粒子群算法的底排参数优化

谢利平,史金光,李元生,邱海迪,黄玉才

(1.南京理工大学 能源与动力工程学院,南京 210094;2.沈阳炮兵学院 电子侦察系,沈阳 110867;3.中国船舶工业系统工程研究院,北京 100094)



基于遗传粒子群算法的底排参数优化

谢利平1,2,史金光1,李元生3,邱海迪1,黄玉才1

(1.南京理工大学 能源与动力工程学院,南京 210094;2.沈阳炮兵学院 电子侦察系,沈阳 110867;3.中国船舶工业系统工程研究院,北京 100094)

为优化底排装置结构和药柱燃速系数,以某型底部排气弹为例,分析确立了设计变量和目标函数,综合遗传算法和粒子群优化的优点,设计了遗传粒子群优化算法,结合建立的底排内外弹道模型,构建了基于GA-PSO的底排参数优化模型。算例中优化方案能增加底排弹的减阻率,底排工作时间延长9.56 s,落点存速增加6.01 m/s,最大射程增加1 892.95 m,增幅5.02%。该文设计的GA-PSO具有较好的稳定性和较快的收敛速度,优化模型可以为底部排气弹底排装置的设计提供参考,也可以作为其他相似寻优问题的基本模型。

底部排气弹;增程;参数优化;遗传粒子群算法

底排增程是目前广泛使用的一种减阻增程方法,该方法通过向弹底低压区排入具有一定质量和能量的燃气、提高底压来达到减阻增程的目的[1]。底排的减阻性能与底排装置结构、药剂燃速等密切相关,同时也受底排内外弹道环境条件、飞行状况等因素的影响,因此如何设计底排装置结构、优化底排药剂燃速将直接关系到底排弹的减阻增程效果。

目前,国内外关于底部排气弹的研究主要集中在利用数值模拟方法研究底排弹底部流场与减阻性能[2-5],利用风洞实验研究环境温度和压力对底排的影响[6,7]以及特定条件下的底排减阻特性[8-11]等,有关底排参数优化的问题研究较少。而在众多的优化方法中,遗传算法(genetic algorithm,GA)作为一种全局优化算法,它启发于生物的遗传与进化过程,具有全局搜索能力强、稳定性好、易于并行等优点,但算法效率有待于提高[12];粒子群优化(particle swarm optimization,PSO)则是模仿鸟类群体搜索食物过程,是一种基于自身学习和社会学习的智能优化算法,有很强的通用性,粒子间学习能力较强,原理简单,便于实现,但搜索精度不高,易陷入局部最优[13]。

针对底排参数优化问题的现状以及上述2种算法的优缺点,本文设计了遗传粒子群优化算法(GA-PSO)作为问题寻优的基本方法,建立了底排内外弹道模型,并将两者有机结合，构建了基于遗传粒子群算法的底排参数优化模型。模型所使用的遗传粒子群算法充分利用遗传算法的优秀基因遗传进化特性和粒子群算法的自我认知和社会学习能力,采用“父代遗传+自身学习”的优化模式,更符合生物进化理论和人类发展过程。底排内外弹道模型考虑了飞行马赫数变化、高转速环境、全弹道飞行条件等的影响,为精确的底排参数优化提供了保证。

1　问题描述

底部排气弹是利用底排装置通过向弹底低压区排入具有一定质量和能量的燃气,进而提高底压来达到减阻增程的目的。底排装置设计参数、评价指标有多种,因此首先要分析并确定其优化设计变量、约束条件和目标函数。

1.1设计变量

底排弹减阻增程效果主要取决于底排装置的结构参数、药柱燃速系数等因素。底排开始工作时间选择在炮口最有利于发挥减阻增程作用[14],底排装置的结构参数、药柱燃速系数确定之后,底排药柱燃速、燃面变化规律,燃气质量流率,底排工作时间等量也即确定。因此本文选用底排药柱燃速系数b以及底排药柱长度LB、初始内半径r0、分瓣数nB、喷口直径dnoz等5个参数作为底排优化设计变量。

1.2约束条件

约束条件是对设计变量的取值给予一定限制的数学关系式,也是对优化设计问题本身提出一些条件限制,使设计方案在满足这些限制条件下达到较优。对于底排参数优化模型,应满足以下约束条件。

①设计变量取值范围约束。底排药长、初始内半径、分瓣数、喷口直径等参数的取值应综合底排弹实际情况进行约束:xd,min≤xd≤xd,max,其中,xd,max,xd,min分别为设计变量xd的取值上、下限。

②底排药剂质量约束。过大的底排药剂质量对于底排弹的质心位置、转动惯量等都有影响,因此底排药剂质量应满足:mB≤mB,max。

③排气参数约束。对应于一定的马赫数,底排装置具有最佳排气参数,称为极限排气参数Imax,底排装置工作期间应尽量满足I≤Imax。

1.3目标函数

评价底部排气弹性能的参数有多种,例如底压比、减阻率、落点散布、射程等。底部排气弹的最终效果就是增程,因此选用底排弹的最大射程作为目标函数进行设计变量优化效果的评价值。同时,对于不满足相关约束条件的优化方案,引入罚函数,将有约束问题转化为无约束问题进行求解。底排弹射程Lran与设计变量的关系可表示为

Lran=f(X),X=(x1x2…xD)T

(1)

引入罚函数的目标函数Ltar可表示为

(2)

式中:X是由设计变量x1,x2,…,xD组成的列向量,下标D为设计变量个数;Ltar是对应于一组设计变量的目标函数值(适应度);ks,Δcs分别为第s个约束的罚因子和性能指标超过约束条件的量值。

2　底排参数优化数学模型

确定了设计变量及目标函数后,需要建立设计变量与目标函数之间的联系,即要建立底排弹射程与底排参数之间的数学关系Lran=f(X),因此需要首先建立底排弹内弹道和外弹道模型,进而构建底排参数优化数学模型。

2.1底排内弹道模型

根据空气动力学知识,建立以底排药柱燃烧内径、生成燃气质量、内压力等为变量的底排内弹道微分方程:

(3)

式中:pmot为底排装置内压力;ρB为底排药剂密度;r,c分别为随燃烧不断变化的底排药柱内孔半径和扇形药柱间的狭缝宽;Sr,Sc分别为对应的燃烧面积;vr,vc分别为对应的燃速。考虑弹丸旋转的指数燃速定律可表示为

(4)

(5)

式中:Se为排气喷口截面积;Tmot为药柱燃烧温度;R,k分别为燃气的气体常数和绝热指数;pe,pmot分别为喷口附近环境压力和底排装置内压力;nB为药柱分瓣数;LB为底排药柱长度;r2为底排药柱扇形药块外圆弧半径。

(6)

式中:ρ∞,v∞分别为来流密度、速度;I为排气参数;Sb为弹底面积;Ma为飞行马赫数;RcDB为底阻减阻率,是马赫数Ma与排气参数I的函数;A为对应的3×3系数矩阵,利用风洞实验测定;cD为总阻力系数;cD0为底排不工作时的总阻系数;cDB0为底排不工作时的底阻系数;kcD为总阻减阻率。

2.2底排外弹道模型

底排外弹道模型中弹丸运动方程组采用刚体六自由度模型。在弹道坐标系中建立的质心运动方程和弹轴坐标系中建立的绕心运动方程如下:

(7)

(8)

式中:Ω,ω1分别为弹道坐标系和弹轴坐标系的转动角速度;Fx2,Fy2,Fz2为外力矢量F沿弹道系各轴分解的分力;Mξ,Mη,Mζ为外力矩M沿弹轴系各轴分解的分力矩。以上各物理量表达式详见参考文献[15]。通过联立底排内外弹道模型方程组,即可求解某一组设计变量Xi=(xi1xi2…)T对应的底排弹射程Lran=f(Xi)。

2.3底排参数优化模型

综上所述,建立底排参数优化模型如下。

目标函数:

(9)

约束条件:

(10)

式中:f(X)为一组优化方案对应的底排弹射程,通过上述底排弹道模型进行计算得到。

3　遗传粒子群优化算法的设计

3.1遗传算法

遗传算法是一种基于生物自然选择与遗传机理的自适应全局优化概率搜索算法,其生物学原理是模拟自然界遗传机制和生物进化过程。在遗传算法中,群体中每个个体是问题的一个解向量,称为染色体。染色体在后续迭代中不断进化,称为遗传。算法通过不断地选择、交叉、变异等操作,将优秀个体基因遗传到下一代。这样经过若干代之后,算法收敛于最好的染色体,即问题的近似最优解。

设在D维目标搜索空间中,种群中个体数为lg,第i个个体表示为Xi=(xi1xi2…xiD)T,i=1,2,…,lg。首先代入目标函数计算个体适应度值,然后计算出此适应度值在群体适应值总和中的比例,作为该个体在选择过程中被选中的概率。选择过程采用轮盘赌的方式,对于个体Xi,设其适应度值为f(Xi),其被选中的概率为

(11)

(12)

式中:q为[0,1]区间的随机数,对于不同个体、不同位置的交叉操作,q值通常不同。在遗传算法变异操作中,对于每个个体Xi的每个位置xid(d=1,2,…,D),以一定的概率Pmut进行变异,变异操作如下:

(13)

式中:qid为[-1,1]区间的均匀随机数,Δxid是对应于xid的变异范围。

3.2粒子群优化算法

粒子群优化算法源于对自然界中鸟群等生物群体觅食行为的仿真研究,通过个体“学习”优秀者的行为,其表现型逐渐向优秀者靠近。PSO算法基本步骤为:设在D维目标搜索空间中,有lp个粒子组成一个粒子群,lp是种群规模;第i个粒子表示为Xi=(xi1xi2…xiD)T,i=1,2,…,lp,每个粒子的位置Xi是问题的一个潜在解,将其代入目标函数可计算其适应度值,根据适应度的大小来衡量相应粒子的优劣。粒子向优秀者“学习”的过程称为“飞翔”,第i个粒子的“飞翔”速度表示为vi=(vi1vi2…viD)T。粒子速度与位置更新通过以下2个公式进行操作:

(14)

(15)

式中:i=1,2,…,lp,d=1,2,…,D;D是解向量维数;世代数n=1,2,…;w为惯性权重,c1,c2为加速常数;q1,q2为[0,1]之间的随机数;xbest为该粒子记录的最优位置,xglobal为全局最优位置。为获得更好的寻优结果,惯性权重采用线性递减权值策略[16],第n代惯性权重wn的计算公式为

wn=[(wstart-wend)·(N-n)/N]+wend

(16)

式中:wstart,wend分别为初始时和终止时惯性权重;n为当前代数;N为最大迭代次数。

3.3遗传粒子群优化算法

遗传算法通过选择、交叉、变异等遗传操作能将父代优秀基因遗传给子代,同时又具有很强的全局搜索能力,但计算时间的增长使得求解效率降低;粒子群优化算法中粒子能够比较自身及群体优秀者,通过向优秀者学习来提高自身适应度,模仿了自我认知和社会学习机制,操作简单,收敛较快,但易陷入局部最优。

因此,综合遗传算法和粒子群算法各自优点,充分利用遗传算法的优秀基因遗传特性和粒子群算法的学习能力,本文设计了一种新的遗传粒子群(GA-PSO)混合算法,该算法采用“父代遗传+自身学习”的优化模式,更符合生物进化理论和学习发展过程。该算法首先随机生成l0个个体(或粒子),进行一次遗传操作后根据适应度值排序,并分成两部分:较优的lb个个体和较差的l0-lb个个体;对较优的lb个个体进行遗传优化,而对较差的l0-lb个个体进行粒子群优化;将由此得到的新的l0个个体再按上述步骤重复进行,直至满足终止条件。GA-PSO算法优化过程如图1所示,基本操作公式如式(11)～式(16)所示。

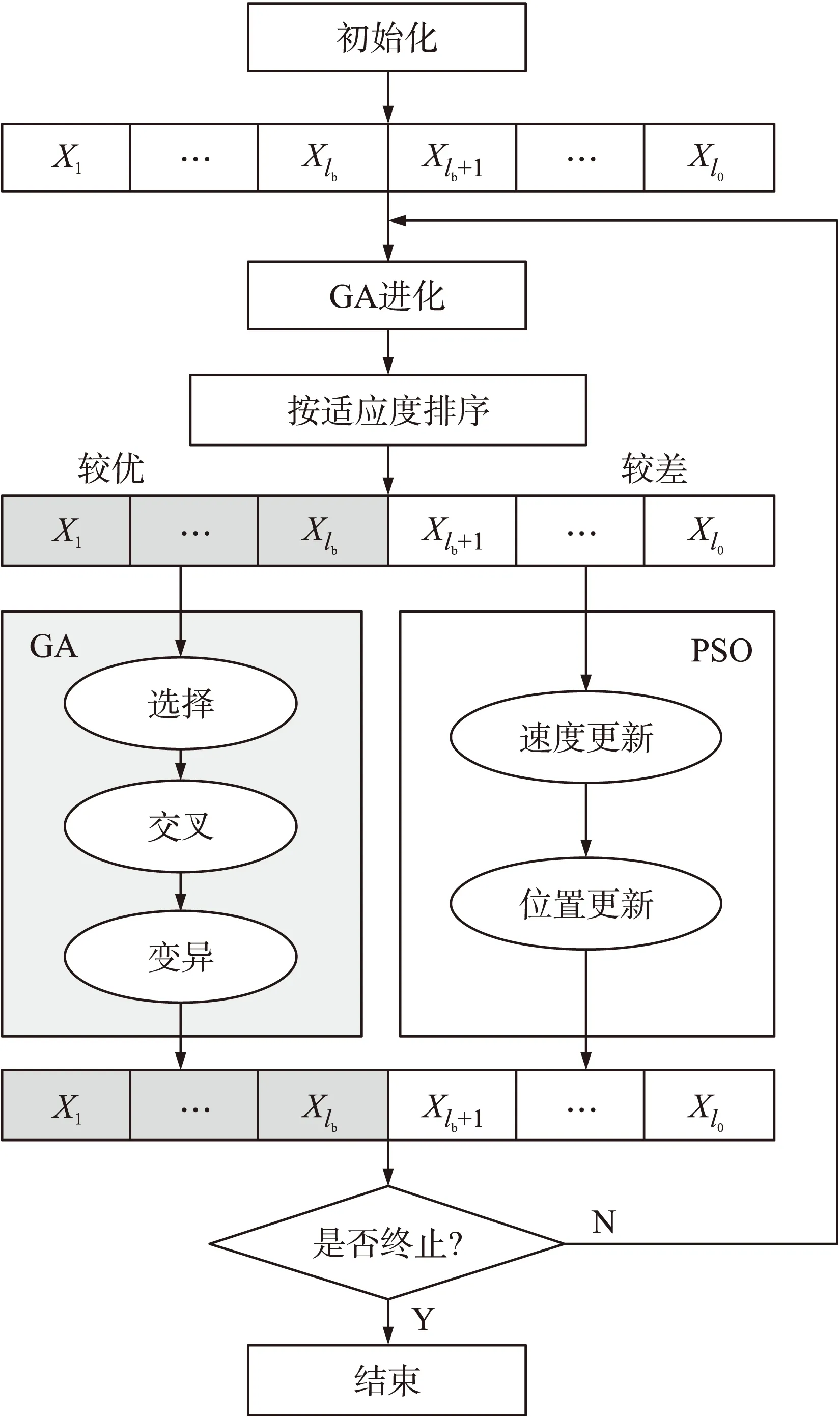
图1　GA-PSO算法优化过程

将底排弹道模型与GA-PSO算法连接就形成了底排参数优化模型,模型的主要流程如图2所示。

图2　底排参数优化模型示意图

4　优化算例

根据上述底排参数优化模型编制了计算程序,以某型底部排气弹为例,弹丸初速v0=930m/s,采用射角θ0=52°时的射程近似作为最大射程,用上述方法对底排参数进行优化设计。表1给出了设计变量取值范围,各变量符号如前所述。表2给出了GA-PSO算法的参数设计,表中,mg,mp和Ng,Np分别是GA部分和PSO部分的种群规模和最大迭代次数。设计变量及相关参数在优化前的参考取值和优化后取值如表3所示,表中,tB为底排工作时间,vend为落点存速,其余变量含义如前所述。从表3可

以看出,优化前后底排弹射程增加1 892.95m,增幅达到5.02%。同时,底排工作时间延长9.56s,落点存速增加6.01m/s,可使底排弹在落点处动能增大3.12%。

在一定范围内底排药长增加使燃气质量流率增大,底排减阻效果增强;但随着底排药长的进一步增加,过大的排气参数使得底排燃气从喷口排出时动能过大,对底部回流区的引射作用更加明显,反而会抵消部分减阻效果,降低增程率。同样,底排药剂燃速系数的增加会引起排气参数的增大,增加底排弹减阻增程效果;而药剂燃速如果过快,不仅会缩短底排工作时间,还会使得排气参数达到甚至超过极限排气参数Imax,使底排药柱产生“浪费”,甚至使燃气非亚音速喷出,导致增程率减小。底排药柱长度和燃速系数的优化结果也证实了以上观点。此外,底排药柱初始内半径越小可供利用的底排燃气就越多,有利于射程的增加;喷口直径的适当增大会使底排内压力减小,避免燃气喷出速度过大,能有效防止燃气引射作用,从而加强减阻增程效果;增加药柱分瓣数能增大初始阶段药柱燃烧面积,使底排弹在底排工作初期就获得较大减阻率,有效提高了射程。底排参数的优化结果也符合上述分析。图3所示为底部排气弹在优化前后总阻减阻率随底排工作时间的变化情况,从图中看出,优化方案使得底部排气弹在初期就获得了较大的总阻减阻率,同时延长了底排工作时间。

表1　底排设计变量取值范围

表2　GA-PSO算法中参数设计

表3　底排设计变量及相关参数优化前后对比

图3　优化前后总阻减阻率随底排工作时间的变化

粒子群算法、遗传算法和遗传粒子群算法寻优过程中最大适应度值随迭代次数(世代数)n的变化如图4所示。从图中可以看出,本文提出的遗传粒子群算法避免了粒子群算法早熟和遗传算法收敛慢的缺点,在稳定性与收敛性方面均较优,是一种理想的寻优方法,运用该方法进行相关问题的优化设计可以得到较好的优化方案。运用遗传粒子群算法进行底排参数优化过程中最大适应度值、平均适应度值随迭代次数(世代数)n的变化如图5所示。图中显示当代平均适应度值能较快收敛且波动较小,进一步验证了算法的稳定性与快速收敛性,优化方案相对于参考方案在适应度方面有较大改善。

图4　不同算法寻优过程对比

图5　GA-PSO算法适应度随迭代次数的变化

5　结论

本文建立了底部排气弹内外弹道模型,提出了基于遗传粒子群优化(GA-PSO)的混合算法,并将两者有机结合组成了底排参数优化模型,对某型底部排气弹进行了算例优化及结果分析。优化结果表明:GA-PSO同时避免了粒子群算法早熟和遗传算法收敛慢的缺点,具有较好的稳定性和较快的收敛速度;相比于参考方案,基于GA-PSO的底排参数优化方案能增大底排弹的减阻率,底排工作时间延长9.56s,落点存速增加6.01m/s,落点处底排弹动能增大3.12%,最大射程增加1 892.95m,增幅5.02%。优化方案可以为底部排气弹底排装置的优化设计提供参考,基于GA-PSO的底排参数优化模型可以作为其他类型寻优问题的基本模型。

[1]郭锡福.底部排气弹外弹道学[M].北京:国防工业出版社,1995.

GUO Xi-fu.Exterior ballistics of base bleed projectiles[M].Beijing:National Defense Industry Press,1995.(in Chinese)

[2]卓长飞,封锋,武晓松.超声速底部排气弹底部流场与气动特性研究[J].空气动力学学报,2014,32(6):783-790.

ZHUO Chang-fei,FENG Feng,WU Xiao-song.Research on base flow field and aerodynamic characteristics of the supersonic base bleed projectile[J].Acta Aerodynamica Sinica,2014,32(6):783-790.(in Chinese)

[3]谭慧俊,郭荣伟.底部排气法的减阻特性及在超声速导弹上的应用[J].南京航空航天大学学报,2004,36(6):677-682.

TAN Hui-jun,GUO Rong-wei.Drag reduction of base bleed method and its application on supersonic missiles[J].Journal of Nanjing University of Aeronautics & Astronautics,2004,36(6):677-682.(in Chinese)

[4]余文杰,余永刚,倪彬.底部排气圆柱体模型尾部流场的数值模拟[J].弹道学报,2014,26(1):7-12.

YU Wen-jie,YU Yong-gang,NI Bin.Numerical simulation of base flow field over a cylindrical model with base bleed[J].Journal of Ballistics,2014,26(1):7-12.(in Chinese)

[5]CHOR J Y,SHIN E,KIM C K.Numerical study of base-bleed projectile with external combustion[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Tucson,Arizona:AIAA,2005:1-6.

[6]丁则胜,陈少松,刘亚飞,等.环境温度对底排效应的影响[J].弹道学报,2003,15(1):37-40.

DING Ze-sheng,CHEN Shao-song,LIU Ya-fei,et al.Influence of ambient temperature on base bleed effect[J].Journal of Ballistics,2003,15(1):37-40.(in Chinese)

[7]丁则胜,陈少松,刘亚飞,等.底排性能的环境压力效应[J].弹道学报,2002,14(1):88-92.

DING Ze-sheng,CHEN Shao-song,LIU Ya-fei,et al.Influence of ambient pressure on base bleed[J].Journal of Ballistics,2002,14(1):88-92.(in Chinese)

[8]陈少松,丁则胜,罗荣,等.亚、跨声速底排减阻特性研究[J].流体力学实验与测量,2000,14(4):41-45.

CHEN Shao-song,DING Ze-sheng,LUO Rong,et al.An investigation on characteristics of base drag reduction with base bleed in subsonic and transonic speeds[J].Experiments and Measurements in Fluid Mechanics,2000,14(4):41-45.(in Chinese)

[9]卓长飞,武晓松,封锋.超声速流动中底部排气减阻的数值研究[J].兵工学报,2014,35(1):18-26.

ZHUO Chang-fei,WU Xiao-song,FENG Feng.Numerical research on drag reduction of base bleed in supersonic flow[J].Acta Armamentarii,2014,35(1):18-26.(in Chinese)

[10]LEE Y K,RAGHUNATHAN S,KIM H D,et al.Computations of the supersonic flow over an afterbody with base bleed[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada:AIAA,2005:1-7.

[11]KAURINKOSKI P.Computation of the flow of thermally perfect gas past a supersonic projectile with base bleed[C]//AIAA Atmospheric Flight Mechanics Conference.San Diego,CA:AIAA,1996:725-734.

[12]葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2008,25(10):2 911-2 916.

GE Ji-ke,QIU Yu-hui,WU Chun-ming,et al.Summary of genetic algorithms research[J].Application Research of Computers,2008,25(10):2 911-2 916.(in Chinese)

[13]TRELEA I C.The particle swam optimization algorithm:convergence analysis and parameter selection[J].Information Processing Letters,2003,85(6):317-325.

[14]郭锡福,魏应彬.底部排气弹减阻特性的合理设计[J].空气动力学学报,1995,13(4):388-395.

GUO Xi-fu,WEI Ying-bin.Reasonable design of drag reduction characteristic of base bleed projectile[J].Acta Aerodynamica Sinica,1995,13(4):388-395.(in Chinese)

[15]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.

HAN Zi-peng.Exterior ballistics of projectile and rocket[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

[16]EBERHART R C,SHI Y.Comparing inertia weights and constriction factors in particle swarm optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation:Evolution at Work,vol.1.La Jolla,California:IEEE,2000:84-88.

Optimization on Base Bleed Parameters Based on Genetic Particle Swarm Algorithm

XIE Li-ping1,2,SHI Jin-guang1,LI Yuan-sheng3,QIU Hai-di1,HUANG Yu-cai1

(1.School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China;2.Department of Electronic Reconnaissance,Shenyang Artillery Academy,Shenyang 110867,China;3.Systems Engineering Research Institute,CSSC,Beijing 100094,China)

To optimize the structure of base bleed device and the burning rate coefficient of grain,a certain type of base bleed projectile was taken as instance,and the design variables and target function were analyzed and established.Considering both advantages of genetic algorithm and particle swarm optimization,a genetic algorithm-particle swarm optimization(GA-PSO)algorithm was designed.Combined with the model of base bleed interior and exterior ballistics,a model of base bleed parameters optimization was established based on GA-PSO.Results show that the optimization scheme can increase the drag-reduce rate,extend base bleed work time for 9.56 s and increase remaining velocity of 6.01 m/s,and the maximum range increases by 1 892.95 m(5.02%).The designed GA-PSO is stable and has a fast convergence speed.The optimization model offers reference for the design of base bleed device,and the model can be a basic model for other similar optimization problems.

base bleed projectile;extended range;parameter optimization;GA-PSO

2015-08-14

中国博士后科学基金项目(2013M541676)

谢利平(1989- ),男,硕士研究生,研究方向为外弹道理论及弹道气象。E-mail:xlp14@163.com。

史金光(1975- ),男,副研究员,博士,研究方向为外弹道理论及弹箭飞行与控制。E-mail:shijg1122@163.com。

TJ012.3

A

1004-499X(2016)01-0033-06