空化器参数对超空泡初生位置影响大涡模拟

张　木,谭俊杰,易文俊,廖选平

(1.中国运载火箭技术研究院 战术武器事业部,北京 100076;2.南京理工大学 能源与动力工程学院,南京 210094;3.南京理工大学 瞬态物理国家重点实验室,南京 210094)



空化器参数对超空泡初生位置影响大涡模拟

张木1,谭俊杰2,易文俊3,廖选平1

(1.中国运载火箭技术研究院 战术武器事业部,北京 100076;2.南京理工大学 能源与动力工程学院,南京 210094;3.南京理工大学 瞬态物理国家重点实验室,南京 210094)

为揭示空化器参数对超空泡初生位置的影响规律,离散求解了三维气液两相大涡模拟控制方程组,对三维不同空化器参数模型下超空泡流动进行了数值模拟。在不同空化数条件下,通过数值模拟获得超空泡无量纲几何参数并与实验数据对比,结果表明两者吻合良好。在此基础上,分析了不同空化器形状、直径对超空泡初生位置影响。分析结果为探索高速航行体空化器性能与水动力特性提供了数值参考。

超空化;大涡模拟;超空泡初生位置;气液两相流动;数值模拟

俄罗斯高速超空泡鱼雷的出现，促使超空泡武器吸引了世界各大军事强国的关注,并纷纷投入大量科研力量开展空化现象的研究。空化流动是一种考虑相变、粘性、湍流运动、界面可压缩性的极其复杂的多相流动现象。早期由于受到多相流理论及计算机硬件设备等条件的制约,研究人员主要利用势流理论方法[1],其中具有代表性的研究有:Helmholtz[2]基于势流理论,分析了绕二维平板的超空泡流动现象;Riabouchinsky[3]提出了有限长度空泡模型。随着多相流理论和计算机硬件设备条件取得长足进展,研究人员开始广泛使用离散求解N-S方程的算法进行机理研究与工程应用[1]。例如:Delannoy和Kueny假设流动状态为等温且不考虑气相与液相的可压缩性,研究了不同模型下的空化流动问题[4-5]。Hesister依托Delannoy的研究结果,优化了混合密度求解方程,引入压力的影响[6]。黄海龙等[7]针对三维圆盘空化器模型,分析了变攻角条件下超空泡流动。周景军、于开平研究了低弗劳德数下通气超空泡泄气机理,揭示了弗劳德数与通气率对空泡泄气的影响规律[8-9]。综合上述分析可知,目前超空泡研究主要集中在大空化数(空化数小于0.01)，采用雷诺平均湍流模型方法。结合国内外相关研究情况,本文研究了小空化数下空化器参数对超空泡初生位置的影响。

1　控制方程

1.1大涡模拟

本文基于VOF方法、大涡模拟湍流模型,以及空化模型,对超空化流动进行数值仿真,其滤波后的控制方程可写为

(1)

(2)

(3)

(4)

(5)

1.2空化模型

为模拟气相与液相间的相变质量传递过程,本文采用Kunz空化模型,其表达式为

(6)

(7)

式中:Cprod,Cdest为模型系数;t∞=L/v∞,L为计算域长度;v∞,ρv,ρl分别为来流速度、气相与液相密度;其他变量参数详见文献[10]。

2　离散方法

本文计算中N-S方程组的对流项、扩散项以及时间项离散方法详见文献[1]。为实现气液交界面的可压缩性计算,引入基于PISO算法的密度-压力-速度耦合算法[10]。

(8)

式中:ap为单元中心项系数,H(U)表示相邻节点项以及源项之和,ΔVp为单元体积。将预估压力分布p*代入式(8)求解出近似速度分布u*,v*,w*。

查看u*,v*,w*在连续性方程中的适应性,若适应性不符合连续性方程条件需进行第1次修正,即求解如下方程:

·(U*)p-

(9)

式中：ΔVp为计算单元体积。式(9)考虑了气液两相界面可压缩性影响。通过式(9)求解出经过第一次校正步后的速度、压力改进值U**和p**。

第2压力修正方程为

·(U**)p+

(10)

将U**,p**代入式(10)所示的第2压力修正方程,求解出流场的速度与压力值。

3　计算结果与分析

3.1计算结果与试验结果对比

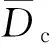
图1　超空泡几何参数随空化数变化

由图1可知,随着空化数增加,空泡长度、直径均降低。本文空泡直径计算结果与经过试验验证的Longvinovich[11]经验公式和Savchenko[12]经验公式吻合良好。本文空泡长度计算结果与Longvinovich经验公式吻合良好,这是由于Longvinovich经验公式适用空化数范围为0～2.5×10-1,而Savchenko经验公式适用空化数范围为1.2×10-3～5.7×10-3。数值模拟结果与试验结果变化趋势基本一致且吻合良好。

3.2不同空化器直径对超空泡初生位置的影响

在FVM(finite volume method)方法计算中,为提高计算效率和精度,本文采用分块结构化网格方法实现三维圆盘空化器航行体模型(长径比为10)网格划分,如图2所示。

本文计算对象的航行速度小于水下声速,为保证航行体表面的流动不会受到远场的影响,并且考虑到超空泡长度的影响,本文选取如图3所示的计算域范围。除计算域右端为压力出口边界条件外,其余均为速度入口边界条件,航行体表面为固壁边界条件,速度为无滑移边界条件。

在空化器直径分别为Dn=5 mm,3.5 mm,2 mm;攻角α=0°,空化数σ=2.17×10-3条件下,对圆盘空化器航行体超空泡流动现象进行了计算,分析了空化器直径对超空泡初生位置的影响。计算结果如图4所示,图中,φl表示液相体积分数。

图2　计算网格

图3　计算域示意图

图4、图5分别为不同空化器直径下空泡等值面图和液相体积分数图。由图4、图5可知,当Dn=2 mm时,航行体表面无法被空泡整体覆盖,头部空化器和航行体表面部分区域外露,处于粘湿状态,头部超空泡初生位置距离空化器顶点明显靠后,尾部超空泡初生位置出现在锥-柱连接处,这样会导致航行体受力特性发生变化,对航行体运动稳定性和水动力特性存在较大影响。当3.5 mm≤Dn≤5 mm时,航行体表面完全被空泡整体覆盖,超空泡初生位置出现在空化器顶端,且航行体表面空泡厚度随空化器直径增加而增厚,空泡空化效果越好。航行体上表面空泡厚度随空化器直径的变化曲线如图6所示，图中，X/L表示航行体无量纲轴向位置,h表示上表面空泡厚度。

图4　不同空化器直径下空泡等值面图

图5　不同空化器直径下液相体积分数图

图6　航行体上表面空泡厚度随空化器直径变化曲线

由图6可知,从航行体头部前缘起,当Dn=2 mm,0≤X/L≤0.6时,空化器直径小导致航行体表面无法被空泡整体覆盖,因此上表面空泡先增大再减小到0;当Dn=2 mm,0.6

柱连接处形成低于临界空化压力区,再次产生尾端空泡,因此上表面空泡最后逐渐增大。从航行体头部前缘起,当3.5 mm≤Dn≤5 mm,0≤X/L≤1时,由于航行体表面完全被空泡整体覆盖,因此在空化器直径不变条件下, 上表面空泡整体呈增大趋势。

在无量纲轴向位置相同情况下,当2 mm≤Dn≤5 mm时,上表面空泡随空化器直径增加而变厚。

3.3不同空化器形状对超空泡初生位置的影响

在α=0°,σ=2.17×10-3,Dn=5 mm条件下,计算了3种典型空化器头型航行体超空泡流动,结果如图7所示; 小空化数条件下不同空化器形状对空泡初生位置的影响规律如图8、图9所示。

图7　超空泡几何参数随空化数变化

图8　不同空化器形状下航行体液相体积分数云图

图9　不同空化器形状下航行体头部空泡等值面图

由图可知,圆盘空化器模型头部超空泡初生位置距离空化器顶端0 mm,1/4球形空化器模型头部超空泡初生位置距离空化器顶端2.46 mm,而150°锥角圆锥空化器模型头部超空泡初生位置位于两者之间,其距离空化器顶端1.05 mm。由此可得出,在空化数、空化器直径以及攻角一定的条件下,圆盘空化器航行体的粘湿面积最小,1/4球形空化器航行体的粘湿面积最大。此外,为保持超空泡航行体的运动稳定性,应尽可能减小航行体的粘湿面积。综合上述分析可知,在空化数、空化器直径以及攻角一定的条件下,圆盘空化器的超空泡初生位置出现在空化器顶端,具有良好的超空泡生成能力。

4　结论

本文离散求解三维气液两相大涡模拟控制方程组,探究了绕三维不同空化器参数航行体模型的超空泡流动现象,揭示了小空化数下不同空化器参数对超空泡初生位置的影响并获得如下相关结论:

①通过数值模拟获得了无量纲空泡几何参数随空化数的变化规律,并且本文数值模拟结果与Logvinovich、Savchenko试验结果吻合良好。

②揭示了超空泡初生位置随空化器直径的变化规律,分析结果显示,当Dn=2 mm时,航行体表面无法被空泡整体覆盖,头部超空泡初生位置距离空化器顶端明显靠后,尾部超空泡初生位置出现在锥柱连接处,导致航行体受力特性发生变化,影响运动稳定性;当3.5 mm≤Dn≤5 mm时,航行体表面完全被空泡整体覆盖,超空泡初生位置位于空化器顶端。

③探究了不同空化器形状对超空泡初生位置的影响,分析结果表明,在空化数、空化器直径以及攻角一定的条件下,圆盘空化器模型的超空泡初生位置出现在空化器顶端,具有良好的超空泡生成能力。

[1]张木,易文俊,谭俊杰,等.带尾翼水下自然超空泡射弹数值模拟研究[J].计算力学学报,2013,30(1):161-165.

ZHANGMu,YIWen-jun,TANJun-jie,etal.Numericalinvestigationofunderwaternaturalsupercavitatingprojectilesoperatingwiththeempennages[J].ChineseJournalofComputationalMechanics,2013,30(1):161-165(inChinese)

[2]NOURINM,ESLAMDOOSTA.Aniterativeschemefortwo-dimensionalsupercavitatingflow[J].OceanEngineering,2009,36(9):708-715.

[3]RIABOUCHINSKYD.Onsteadyfluidmotionwithfreesurfaces[J].ProceedingsoftheLondonMathematicalSociety,1921,19(1):206-215.

[4]DESHPANDEM,FENGJ,MERKLECL.CavityflowpredictionsbasedontheEulerequations[J].JournalofFluidsEngineering,1994,116(1):36-44.

[5]KARIMMM,AHMMEDMS.NumericalstudyofperiodiccavitatingflowaroundNACA0012hydrofoil[J].OceanEngineering,2012,55(15):81-87.

[6]CHENY,HEISTERSD.Modelinghydrodynamicnonequilibriumincavitatingflows[J].JournalofFluidsEngineering,1996,118(1):172-178.

[7]黄海龙,魏英杰,黄文虎,等.重力场对通气超空泡影响的数值模拟研究[J].哈尔滨工业大学学报,2007,39(5):800-803.

HUANGHai-longWEIYing-jie,HUANGWen-hu,etal.Numericalsimulationstudyoftheinfluenceofgravityfieldontheventilatedsupercavity[J].JournalofHarbinInstituteofTechology,2007,39(5):800-803.(inChinese)

[8]周景军,于开平,杨明.低弗鲁德数条件下通气超空泡泄气机理数值模拟[J].工程力学,2011,28(1):251-256.

ZHOUJing-jun,YUKai-ping,YANGMing.NumericalsimulationofgasleakagemechanismofventilatedsupercavityundertheconditionoflowFroudenumber[J].EngineeringMechanics,2011,28(1):251-256.(inChinese)

[9]YUKai-ping,ZHOUJing-jun,MINJing-xin,etal.AcontributiontostudyontheliftofventilatedsupercavitatingvehiclewithlowFroudenumber[J].JournalofFluidsEngineering,2010,132(11):1-7.

[10]张木,谭俊杰,易文俊,等.非定常水下超空泡射弹大涡模拟研究[J].弹道学报,2012,24(3):91-95.ZHANGMu,TANJun-jie,YIWen-jun,etal.Largeeddysimulationofthree-dimensionunsteadyflowoverunderwatersupercavitatingprojectile[J].JournalofBallistics,2012,24(3):91-95.(inChinese)

[11]SEVCHENKOYN,SEMENENKOVN,SEREBRYAKOVVV.Experimentalstudyofthesupercavitationflowsatsubsonicflowvelocities[J].DokladyANUkrainy,1992,42(2):64-69.

[12]SEVCHENKOYN.Experimentalstudyofhigh-speedcavitationflow[J].Hydromechanics,1998,72(1):103-111.

LargeEddySimulationAnalysisonEffectofCavitatorParameteronSupercavityPrimaryPosition

ZHANGMu1,TANJun-jie2,YIWen-jun3,LIAOXuan-ping1

(1.PWD,ChinaAcademyofLaunchVehicleTechnology,Beijing100076,China;2.SchoolofEnergyandPowerEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China;3.StateKeyLaboratoryofTransientPhysics,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Inordertorevealtheeffectofcavitatorparameterontheprimarypositionofsupercavity,thethree-dimensiongas-liquidLES(largeeddysimulation)Navier-Stokesequationswerediscretedandsolved.Thenumericalsimulationofthree-dimensionsupercavitatingphenomenonflowaroundnavigationbodieswithdifferentcavitator-parameterswerecarriedout.Thedimensionlessgeometricparametersofsupercavityundertheconditionsofdifferentcavitationnumberswereobtained.Thecalculationresultwascomparedwithexperimentalresult.Thenumericalresultagreeswellwiththeexperimentalresult.Onthisbasis,thesupercavitatingflowsaroundnavigationbodywhichhasbeencalculatedatdifferentcavitatordiametersandcavitator-shapes.Theeffectsofdifferentcavitator-shapesanddiametersonsupercavitypromarypositionwereanalyzed.Theanalysisresultoffersacademicreferenceforthestudyofhydrodynamicsandcavitatorperformanceofhigh-speedbodies.

supercavitation;largeeddysimulation;supercavityprimaryposition;gas-liquidflow;numericalsimulation

2015-04-08

张木(1985- ),男,工程师,博士,研究方向为多相流场数值模拟。E-mail:nanjingzhangmo@163.com。

O351.3

A

1004-499X(2016)01-0087-05