侧喷管脉冲发动机内流场数值模拟

吴佳男,余　陵,蔡文祥

(南京理工大学 机械工程学院,南京 210094)



侧喷管脉冲发动机内流场数值模拟

吴佳男,余陵,蔡文祥

(南京理工大学 机械工程学院,南京 210094)

为研究侧喷管脉冲发动机的性能,运用流体计算软件对作为制导弹药推力矢量控制系统执行结构的侧喷管脉冲发动机内的三维流场进行数值模拟,分析了偏心段偏心距离、喷管至偏心段距离、偏心段长度对发动机流场结构和发动机性能参数的影响。研究结果表明:随着脉冲发动机偏心段向上移动,其径向推力减小,推力中心由喷管中心内侧向外侧移动;随着喷管至偏心段距离的增加,径向推力先增大、后减小,推力中心发生阶跃性的变化;受发动机结构的限制,偏心段长度对发动机性能的影响较小;采用的数值模拟方法可以用于侧喷脉冲发动机流场及性能预示计算。

侧喷管脉冲发动机;内流场;发动机性能;数值模拟

侧喷脉冲发动机组技术采用一系列独立的、高冲质比、短脉冲的固体火箭发动机组合在一起,通过控制指令,由点火系统进行有序的点火控制,是一种微小型的固体火箭发动机组技术,具有气动舵等其他执行机构无法比拟的快速响应特征[1]。将侧喷脉冲发动机组应用于火炮,加强了火炮打击移动目标的能力,可减少弹药消耗,满足现代战争对智能化弹药的需求。

美国在研精确制导迫弹(precision guided mortar munition,PGMM)[2]、意大利76 mm CCS(舰载反导弹弹道修正弹)[3]均在弹丸质心周围安装小型固体火箭发动机,有效地提高了迫弹的射击精度。ERINT-1作为美国新一代的防空导弹,采用气动式与力矩式直接力控制方式,其直接力控制亦由180个小脉冲发动机产生。随着脉冲喷气发动机的运用日益广泛,研究人员对其性能及工作过程进行了较为深入的研究。张平等人[4]对T型固体脉冲发动机开展试验研究,对比了2种结构的T型发动机,指出侵蚀燃烧对T型发动机性能的影响很大;意大利航空宇航中心的Ciucci[5]对固体火箭喷管的三维湍流流动进行了数值分析,计算结果可有效预测不对称的压力梯度对发动机喉部的作用,以及喷管内涡流和绕流的位置及流动模式;Arabshahi等人[6]基于N-S方程,采用数值方法对飞行中的固体火箭发动机的内部湍流流动过程进行了分析,所得结果较为准确;文献[7]计算了偏心段直径对侧喷管性能的影响,研究发现单靠增加偏心段直径并不能有效地消除“颈缩效应”;文献[8]采用不同湍流模型对侧喷管流场进行数值计算,研究发现k-ωSST湍流模型能够更好地模拟侧喷管燃气的流通特性。通过分析发现,目前国内外对侧喷管脉冲发动机结构尺寸对发动机性能影响的研究较少,研究深度有待于进一步加强。

为此,本文采用Fluent软件对不同结构尺寸的侧喷管脉冲发动机三维流场进行数值模拟,通过分析侧喷管发动机径向推力大小及径向推力偏离喷管中心的距离等性能指标,系统研究偏心段偏心距离、喷管至偏心段距离、偏心段长度对发动机流场结构和发动机性能参数的影响。

1　数学与物理模型

1.1基本假设

侧喷管固体火箭发动机的工作过程是典型的三维非定常过程。为了简化模拟、分析过程,对流场做出如下假设:

①不考虑燃气流动对发动机的烧蚀;

②不考虑热辐射对壁面的传热;

③不考虑流动中化学反应的影响;

④将燃气视为理想可压缩气体;

⑤不考虑重力等彻体力的影响。

1.2数学模型

采用通用计算流体力学软件Fluent,基于有限体积法对用于描述三维可压缩湍流流场的N-S方程组进行离散,将其变换为相应的代数方程并加以求解。其中,N-S方程组主要由质量守恒方程、动量守恒方程、能量守恒方程等组成,可写成如下通用形式[9]:

(1)

式中:Φ为通用变量,可代表速度分量和温度等变量;Γ为广义扩散系数;S为广义源项;ν为比体积。上述变量可在不同的控制方程中具有不同的表达式。

在侧喷脉冲发动机内流动中含有分离流动,可选择k-ωSST两方程模型以较好地模拟流动的逆压梯度及分离过程。在该模型中,湍动能k方程及湍流比耗散率ω的求解公式分别为

(2)

Gω-Yω+Dω+Sω

(3)

式中:Gk,Gω分别为k,ω的生成项;Γk,Γω分别为k,ω的扩散项;Yk,Yω分别为k,ω的耗散项;Sk,Sω为自定义源项,其他参数定义参见文献[10]。

1.3物理模型

本文对侧喷脉冲发动机燃烧室头部、隔热部件以及喷管的内部流场进行了数值分析,发动机结构如图1所示。本文对发动机内部关键结构参数(如图2所示)进行了定义,从而系统研究相关结构对发动机性能的影响。

图1　发动机结构图

对发动机内流场进行了必要的简化,有效地提高了网格质量,提高了计算的效率和准确性。物理模型:燃烧室区域,内径为15 mm，长度为13.1 mm;偏心段,内径为10 mm,长度为11.5 mm;喷管,喉部直径为6.9 mm,扩张比为1.86,长度为8.5 mm。对比不同的偏心距离a、喷管至偏心段距离b及偏心段长度c对发动机流场结构和发动机性能参数的影响,本文计算分析了表1所示的3组尺寸侧喷管脉冲发动机。结合表1及图3,偏心段偏离燃烧室向下为“-”,向上为“+”;喷管底面低于偏心段为“-”,高于偏心段为“+”;径向推力中心偏在喷管外侧为“+”,偏在喷管内侧为“-”。

图2　计算模型

a/mmb/mmc/mm第1组-2.5,-2.2,-2,-1.5,-1,-0.5,0,0.5,1,1.5,2,2.50.511.5第2组-2.2-2,-1.5,-1,-0.5,0,0.5,1,1.5,2,3,4,6,811.5第3组-2.20.56,8,10,10.5,11,11.5,12,12.5,13,14,16

采用ICEM对计算模型划分非结构网格,如图3所示。受物理模型结构、尺寸的影响,计算域网格为50万～65万。为准确地模拟近壁面的流场,对近壁面网格进行加密处理。

图3　网格模型

1.4边界条件

物面条件:采用无滑移的绝热条件,物面附近网格较密,认为附面层假设成立。

入口条件:根据试验的压力曲线,通过曲线积分平均取平均压力23.2 MPa;燃气温度取3 200 K。

出口边界:出口压力设为标准大气压101 325 Pa,出口主要是超声速流动,外推得到。

2　计算结果及分析

2.1偏心段偏心距离对流场和发动机性能的影响

图4(a)、4(b)分别给出了第1组尺寸发动机的径向推力F及径向推力偏离喷管中心距离d的变化规律。从中可以发现,随着偏心段不断向上偏移,径向推力不断变小,且偏心距离在0 mm附近时,推力变化速率最慢;径向推力的推力中心由喷管外侧向喷管内侧移动,呈线性变化规律,在0 mm附近时推力中心偏移量较小。

图4　发动机性能随偏心段偏心距离的变化

图5～图7分别给出了偏心段偏心距离为-2.5 mm,0 mm,2.5 mm的发动机对称面流场的压力p的云图、流线,速度云图,湍粘性系数μt云图。从图5(a)可以看出燃气流经通道最大的特点是燃烧室和喷管由90°拐角连接。从图6(a)、图6(b)可看出侧喷脉冲发动机流场的基本结构:流体从燃烧室进入偏心段后,由于通道面积减小,流体第1次膨胀加速;流体接近拐角,在离心惯性力作用下,流体在拐角外侧出现逆压梯度,有较强回流区,从而使有效通道面积减小;在拐角内侧出现局部逆压梯度,流场在内侧靠近喉部的地方出现回流区,有效喉颈减小,致使质量流率减少,喷管有效膨胀比增大,从而使喷管出口速度增大、压强减小,这种现象被称为“颈缩效应”[5],在有效通道面积和有效喉颈减小的共同作用下,流体在拐角处第2次膨胀加速。流体进入喷管段之后,由于喷管先收敛后扩张的结构特点,流体在喷管内第3次膨胀加速。

图5　偏心段偏心距离-2.5 mm时发动机流场与参数分布

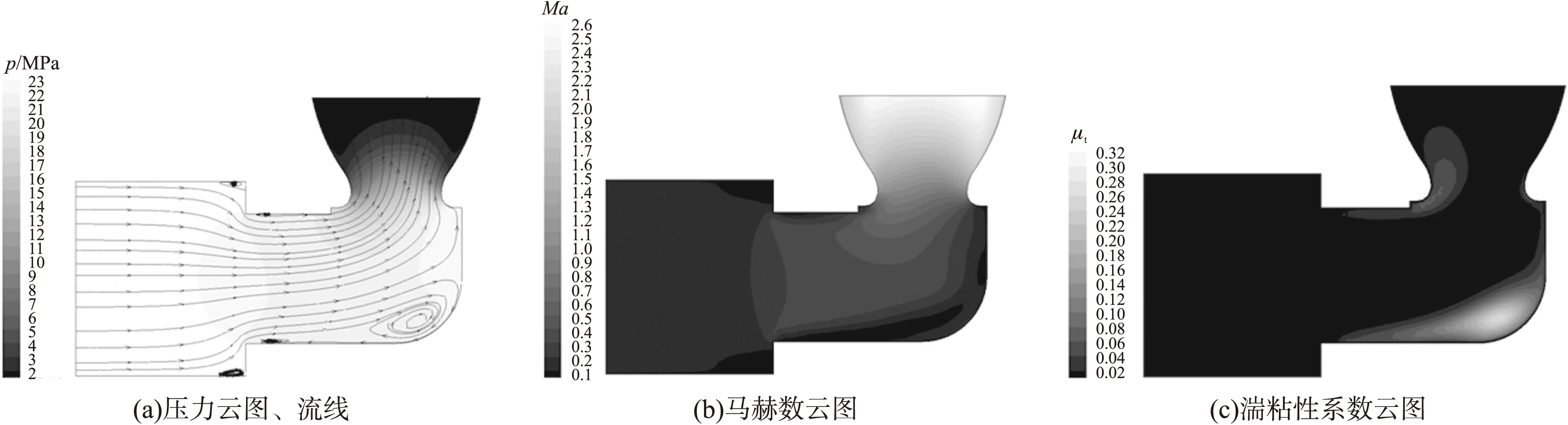
图6　偏心段偏心距离0 mm时发动机流场与参数分布

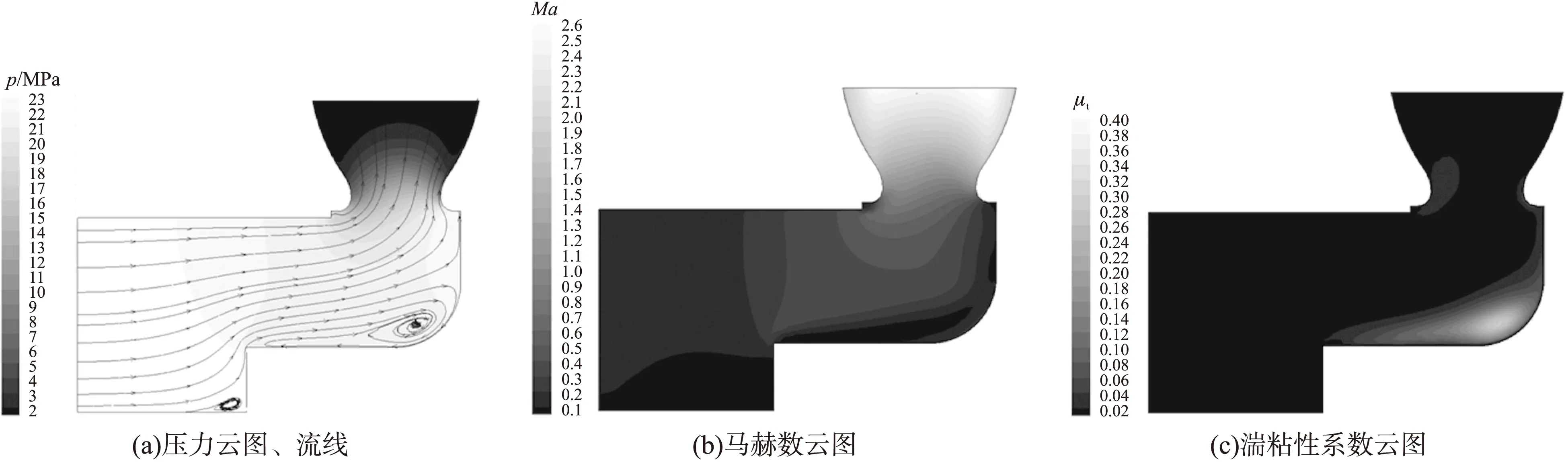
图7　偏心段偏心距离2.5 mm时发动机流场与参数分布

从图5(a)、图6(a)和图7(a)可看出,随着偏心段向上移动,偏心段上侧回流区向偏心段下侧移动,拐角内侧靠近喷管部分的膨胀加速增强,拐角外侧回流区增强,侧喷管脉冲发动机的“颈缩效应”加强。观察图5(b)、图6(b)和图7(b)可发现,当偏心距离为-2.5 mm时,沿着偏心段上侧会产生低速回流区,抑制“颈缩效应”的发展;当偏心距离为2.5 mm时,上侧并没有产生低速回流区,因此燃气可以充分地膨胀加速,“颈缩效应”得到了加强。由此可推测,随着偏心段的上移,“颈缩”效应加强,质量流率减小,有效膨胀比增大,出口速度增大,出口压强减小。

从图5(c)、图6(c)和图7(c)可看出,随着偏心段不断向上移动,湍流损失由偏心段上侧及喷管内侧逐渐向拐角外侧移动;而且总体湍粘性系数变大,湍流强度增大,流动损失变大,出口的质量流率减小。在湍流强度较大的地方,流体与固体的换热程度较大,发动机容易遭受热流破坏。因此需要在偏心段及拐角处采用隔热材料,有效地减小传热损失,防止发动机结构被破坏,从而提高发动机的推力。其中图5的喷管内侧湍流强度较大,喷管最容易被破坏。因此侧喷脉冲发动机喷管需要采用抗烧蚀性更强的材料,可以有效地防止喷管烧蚀破坏,提高发动机的效率,增大推力。

2.2喷管至偏心段距离对流场和发动机性能的影响

图8(a)、图8(b)分别给出了第2组尺寸发动机的径向推力大小及径向推力偏离喷管中心距离d的变化规律。图中,b为喷管至偏心段距离。从图8(a)可看出,随着喷管不断向上移动,径向推力先变大,在-1 mm～+1 mm附近维持稳定,然后不断减小,减小的幅度不断变小。由此推测,应存在一个极限值,当喷管高于偏心段的高度超过某个值后,径向推力将不再发生改变。从图8(b)可看出,喷管凹陷于偏心段时,推力中心位于喷管中心内侧2.5 mm处,基本保持不变;当凸起于偏心段时,径向推力中心发生阶跃,径向推力中心突变到喷管外侧0.5 mm处,且不断偏向喷管中心。由此推测,应存在一个极限值,当喷管高于偏心段的高度超过某个值后,径向推力中心将位于喷管中心线上。

图9～图11分别给出了喷管至偏心段距离为-2 mm、0 mm、8 mm的压力云图、流线，速度云图及湍粘性系数云图。

图8　发动机性能随喷管至偏心段距离的变化

图9　喷管至偏心段距离-2 mm时发动机流场与参数分布

图10　喷管至偏心段距离0 mm时发动机流场与参数分布

图11　喷管至偏心段距离8 mm时发动机流场与参数分布

从图9(a)、图10(a)、图11(a)可看出,随着喷管至偏心段距离的增加,喷管喉部“颈缩效应”逐渐减弱,由此推测,当距离足够远之后,侧喷管脉冲发动机喷管喉部“颈缩效应”将消失;拐角内侧竖直部分出现逆压梯度,有回流区,湍流损失较为严重。

从图9～图11可看出,随着喷管的连续上移,发动机的性能参数变化规律有3个阶段。

第1阶段,喷管底端面低于偏心段。从图9(b)、图10(b)可发现:随着喷管上移,喷管突入偏心段的高度逐渐降低,逆压梯度区域变小,偏心段上侧的回流区变小,由凸台造成的湍流损失减少,出口速度增加;由于上侧回流区对喷管的影响逐渐增大,“颈缩效应”有减小的趋势,有效喉颈增大,质量流率增大。

第2阶段,喷管与偏心段相切附近。从图10(b)可看出,随着喷管的上移,凸台对流动的阻碍作用越来越小。由于偏心段上侧本来就存在低速回流区,当突入的高度小于某个值后,喷管底部对流动的阻碍并不明显,逆压梯度区大小基本保持不变,流动损失变化不大,因此发动机的推力基本保持不变。

第3阶段,喷管高出偏心段大于某个值。从图11(b)、图11(c)可看出:随着喷管继续上移,拐角上部逆压梯度区域不断变大,回流区变大,湍流损失不断变大,导致质量流率减小;拐角对侧喷管喉部的影响有逐步减小的趋势,喷管喉部的“颈缩效应”逐渐减弱,由此推测,应存在某个值,当距离大于这个值后,“颈缩效应”将消失;拐角上部内侧的逆压回流区对喷管喉部有一定的影响,造成了喉部中心湍流损失的加大,若喷管至偏心段的距离大于某个值,偏心段上部回流区就不会对喷管喉部产生影响,可能会使喷管效率提高、径向推力提升。

2.3偏心段长度对流场和发动机性能的影响

图12(a)、图12(b)分别给出了第3组尺寸发动机的径向推力大小及径向推力偏离喷管中心的距离变化规律,图中，c为偏心段长度。可以发现：随着偏心段长度的增加,径向推力小幅度增加、径向推力中心逐渐远离喷管中心;当偏心段长度c大于某个值后,径向推力、径向推力偏离喷管中心的距离基本维持稳定。在现有的结构条件下,偏心段的长度8 mm已经是极限值。因此在结构允许的情况下,偏心段的长度对径向推力大小及径向推力偏离喷管中心的距离基本无影响。

图12　发动机性能随偏心段长度的变化

图13、图14分别为偏心段长度为6 mm、10 mm的压力云图、流线，速度云图及湍粘性系数云图。从图13可看出,“颈缩效应”产生的局部逆压梯度与燃烧室内流体互相干涉，使偏心段内初始的膨胀加速减弱,压力升高、速度降低。从图13(a)、图13(b)、图14(a)和图14(b)可看出,当偏心段长度为6 mm时,偏心段内侧逆压梯度区对喷喉影响较大,有效喉颈较小,“颈缩效应”较强,因此质量流率较小,有效膨胀比较大,出口速度较大,压力较小。因此随着偏心段长度的增加,出口速度减小,压力增加,质量流率增加。

图13　偏心段长度6 mm时发动机流场与参数分布

图14　偏心段长度10 mm时发动机流场与参数分布

从图13(c)、图14(c)可看出,当偏心段长度为10 mm时,拐角底部的湍流区域较大、湍流强度较大。偏心段较长时,湍流发展得较为充分,流动损失较大;当偏心段长度大于某个值后,湍流强度将不发生变化,湍流损失将不变。

从图14可看出,当偏心段的长度大于某个值后,随着偏心段长度的增加,发动机的“颈缩效应”基本保持不变,流场参数不会发生明显变化。由此推测,应存在一个值,当偏心段长度大于这个值后,“颈缩效应”产生的局部逆压梯度不会与燃烧室内燃气互相影响,速度及压力将维持稳定,流场及参数分布基本不发生变化,发动机径向推力大小、推力中心将基本维持稳定。

3　结论

本文采用的数值模拟方法可以用于侧喷脉冲发动机流场及性能预示计算,通过对计算结果的分析,可得出以下结论:

①偏心段偏心距离通过影响偏心段内的低速回流区对“颈缩效应”产生影响。随着偏心段向上偏移,低速回流区由偏心段上侧移向下侧,从而使“颈缩效应”产生的膨胀加速得到了加强,速度增加,压力降低,但由于质量流率的减少,径向推力随着偏心段向上偏移而下降。

②喷管底面低于偏心段时,通过喷管底部对流动的影响改变湍流损失及“颈缩效应”;喷管高于偏心段时,“颈缩效应”随喷管至偏心段距离的增加而逐渐减弱、消失,拐角上部内侧的逆压回流区的变化影响了喷喉的效率,从而影响了发动机的性能。

③受发动机结构尺寸的限制,在实际的侧喷管脉冲发动机中偏心段长度不会影响发动机的性能。

[1]谈凤岗.弹道修正弹的概念研究[J].弹箭技术,1998,9(4):1-10.

TAN Feng-gang.Concept development of trajectory correction projectiles[J].Rocket Technology,1998,9(4):1-10.(in Chinese)

[2]王强.21世纪末制导弹药的发展预测[J].制导与引信,2004,5(10):5-10.

WANG Qiang.Development prediction of the terminal guidance ammunition in the 21st century[J].Guidance and Fuze,2004,5(10):5-10.(in Chinese)

[3]岳明凯,曲家辉.弹道修正弹药的关键技术和发展趋势[J].飞航导弹,2009(9):25-28.

YUE Ming-kai,QU Jia-hui.The key technology and development in ballistic trajectory[J].Aerodynamic Missile,2009(9):25-28.(in Chinese)

[4]ZHANG P,ZHOU S G.Experimental diagnoses of interior ballistic anomalies for an impulsive T-thruster,AIAA 92-3051[R].1992.

[5]ALESSANDRO C,GIANLUCA I,MARCELL A.Numerical investigation of 3D two-phase turbulent flows in solid rocket motors,AIAA 1998-3966[R].1998.

[6]ABDOLLAH A,KIDAMBI S,STEPHEN N D,et al.Computational analysis of turbulent internal flow in ballistic solid rocket motors,AIAA 2007-1449[R].2007.

[7]程兴华.固体脉冲发动机设计及优化[D].长沙:国防科学技术大学,2007.

CHENG Xing-hua.Design and overall optimization for solid pulse rocket motor[D].Changsha:National University of Defense Technology,2007.(in Chinese)

[8]罗茜.固体火箭脉冲发动机内流场特性数值研究[D].南京:南京理工大学,2009.

LUO Qian.Numerical analysis of interior flow field in the solid pulse motor[D].Nanjing:Nanjing University of Science and Technology,2009.(in Chinese)

[9]武晓松,陈军,王栋.固体火箭发动机气体动力学[M].北京:国防工业出版社,2005.

WU Xiao-song,CHEN Jun,WANG Dong.Gas dynamics in solid rocket engine[M].Beijing:National Defense Industry Press,2005.(in Chinese)

[10]TOWNSEND A A R.The structure of turbulent flow[M].England:Cambridge University Press,1976:49-53.

Numerical Analysis of Internal Flow Field in Side Nozzle Pulse Motor

WU Jia-nan,YU Ling,CAI Wen-xiang

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Side-nozzle pulse motors as the executive mechanisms of guided ammunition’s thrust vector control system are smart solid propellant rocket motor.To study the characteristics of motors,fluid calculation software was deployed to carry out simulation analysis on the 3D internal flow field.The effects of the eccentric distance of eccentric segment,the height between nozzle and the eccentric segment and the length of eccentric segment on the flow field structure and performance of engine were studied.Results show that the radial thrust decreases with the increase of the eccentric distance of eccentric segment,and the center of the radial thrust moves from the inside to the outside of the nozzle;the radial thrust increases first and then decreases with the increase of the height between nozzle and the eccentric segment,and the center of radial thrust varies sharply;due to the limitations of engine structure,the length of the eccentric section has less effect on the engine.The methods used can be used to simulate the integrated flow field and estimate the performance of engine.

side nozzle pulse motors;internal flow field;engine performance;numerical simulation

2015-08-30

国家自然科学基金项目(51306092)

吴佳男(1991- ),男,硕士研究生,研究方向为脉冲发动机实验及内流场数值分析。E-mail:njustwujianan@126.com。

余陵(1961- ),男,副教授,硕士生导师,研究方向为固体火箭发动机。E-mail:yuling61@mail.njust.edu.cn。

V435

A

1004-499X(2016)01-0019-07