极限运算中常用方法易错点解析

黄　磊

(江苏联合职业技术学院 镇江分院，江苏 镇江 212000)



极限运算中常用方法易错点解析

黄磊

(江苏联合职业技术学院 镇江分院，江苏 镇江 212000)

极限运算是高等数学(特别是微积分)中的基本运算。本文就解答极限问题过程中出现的常见问题加以归纳，结合例题分析，整理典型错解，理清思路并给出教学建议。

极限；错题；分析

微积分是高等数学的核心内容，而极限运算又是微积分中的基本运算。但是由于学生长期习惯于初等数学的思维方式，初学微积分时往往不太适应。极限的基本运算建立在严格的理论基础上，如果对运算的公式、法则与定理掌握不准确，很容易造成运算上的失误，并且还自查不出原因。在遇到相似的题目时，也很难快速找到合适的法则进行解答。这些问题都是教师在教学过程中应当引起重视的地方。

在学生运用极限公式、法则与定理解决求极限问题时，经常会遇到一些容易混淆的问题。下面将通过几个典型例子对这些问题做出分析，以期抛砖引玉。

1　两个重要极限

(1)

(2)

式(1)与式(2)虽然形似，但实际上式(1)适用范围更广。式(1)中x是实数，可正可负，且为连续变量；而式(2)中n只限于正整数。

实际教学过程中，学生经常会犯以下的错误：

(3)

(4)

(5)

详细写出式(5)的演算步骤如下：

=e-2

(6)

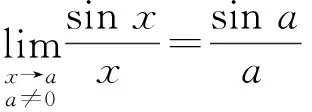
特别注意，式(6)中的变量是弧度制单位。

2　极限四则运算法则

2.1极限存在

=∞-∞

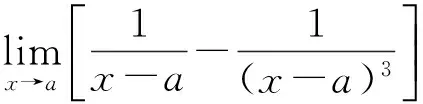
=0

这一解法的第一步是盲目搬用极限的减法法则，第二步是把∞当有限数进行计算，均是错误的。

正确解法如下：

2.2项数有限

法则可推广到函数(包括数列)个数不止两个的情况，但个数只能是有限个，若个数为正无穷大，简单地运用法则就会导致错误的结果。

=0+0+…+0

=0

正确解法如下：

3　极限存在定理

∴无法用极限存在定理来求出。

解1∵sinx有界，

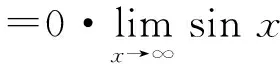
=0

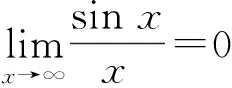
这个问题还有着各种各样的错解，如：

这些错误比较明显，不再赘述。

例4常用规范解法是运用极限存在定理，即

4　总结

求解极限的方法多种多样，在运用不同方法解答时，必须注意强调前提条件，注意适用范围。正确掌握极限的运算方法和运算技巧，对学好微积分课程具有重要意义。在日常教学中，教师要更有效地把握核心内容，让学生少走弯路，让教学更高效。

[1]华东师范大学.数学分析：上[M].4版.北京：高等教育出版社，2010.

[2]同济大学.高等数学：上[M].7版.北京：高等教育出版社，2014.

[3]中国人民大学.微积分[M].北京：高等教育出版社，2004.

[4]景慧丽.极限求解方法研究[J].哈尔滨师范大学学报，2015(5)：16-17.

Analysis of Mistakes in Common Methods of Limit Operations

HUANG Lei

(Zhenjiang Branch of Jiangsu Union Technical Institute，Zhenjiang Jiangsu212000，P.R.China)

Limit operations are basic operations in higher mathematics(especially calculus)．This paper sums up common problems in limit solutions，analyzes examples，sorts out typical wrong solutions，and gives relevant teaching suggestions．

limit；wrong solution；analysis

2016-06-16

黄磊(1983-)，讲师，研究方向为高等数学教学。

O171

A

1008- 8032(2016)04- 0014- 03