一种基于维纳滤波的语音增强算法

［蔡萍］

一种基于维纳滤波的语音增强算法

［蔡萍］

由于各式各样噪声的存在，语音信号的质量会大大地降低，环境噪声的污染造成了许多语音处理系统的功能性急剧降低。维纳滤波是处理噪声污染的可行办法之一。维纳滤波法是一类以极小的均方误差为原则、对平稳过程的最优估计器。对语音信号进行逐帧处理的过程中，传统的维纳滤波法计算短时自相关函数时会遇到求和项数递减的问题，造成自相关函数估计的不准确。针对这一问题，提出一种计算修正自相关函数的改进算法。该算法处理后滤波器系数更加逼近最优值，提高了语音增强的信噪比。

语音增强 维纳滤波 自相关函数

蔡萍

闽江学院物理学与电子信息工程系讲师。

1　引言

语音是人类进行交流的重要工具，已经越来越被人类重视。但是现实生活中，语音中总是掺杂着各种噪声，使得语音失真。语音降噪是解决噪声污染的一种有效方法，其主要目的是尽可能的去除带噪语音中的背景噪声，实现噪声和语音分离，从而使语音信号的质量得到改善［1］。维纳滤波器对带噪语音进行降噪的基本原理是依据最小均方误差法则进行降噪滤波器的设计，带噪语音通过设计滤波器来进行噪声消除，从而获取降噪后较纯净的语音［2］。传统的维纳滤波法计算短时自相关函数时，求和项数递减，自相关函数值趋于衰减，得不到准确的自相关函数的估计。本文提出一种修正后的自相关函数的计算方法，很好地克服了这一问题。

2　维纳滤波算法

设带噪语音信号，纯净语音信号和噪声信号分别为y（k）,x（k）, n（k），y（k）=x（k）+n（k）。将带噪语音信号通过维纳滤波器，输出应尽量逼近x（k）。用e（k）表示真实值与估计值之间的误差，即

显然e（k）是随机变量。维纳滤波的误差准则就是最小均方误差准则，即令达到最小值。

对因果系统而言，

设h（n）是一个因果序列且可用有限长（N点长）的序列去逼近它，则式（3）和（4）变为：

要使得均方误差对小，将上式对各h（m）（m=0,1,…,N-1）求偏导，并且等于零，得：

于是得到N个线性方程：

写成矩阵形式如下：

从维纳-霍夫方程中解出的hopt（m）就是最小均方误差准则下的最佳滤波器系数。写成矩阵形式得［3］：

H=［h（0）,h（1）,…,h（ N-1）］T是待求的单位序列响应。两边取傅里叶变换，得：

设y（k）=x（k）+n（k）中，语音信号x（k）与噪声信号n（k）相互独立，则

故

3　改进的计算方法

式（15）可变成：

计算Pyy（ω）需用到Ryy（0）,Ryy（1）,…,Ryy（N-1）根据语音信号的短时平稳性，对语音信号进行维纳滤波时是逐帧进行的。设帧长为L。对平稳随机过程，自相关函数的计算式为：

设该平稳随机过程具有各态历经性，将统计平均转化为时间平均得一帧内的短时自相关函数：

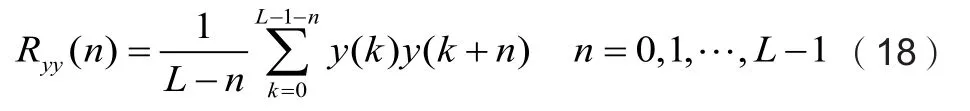
采用式（18）计算出来的短时自相关函数，其幅度上是一个逐渐衰减的曲线。这是由于在计算短时自相关时，窗选语音段的有限长度为L，而求和上限是L-1-n，因此当n增加时可用计算的数据就越来越少了，从而导致n增加时自相关函数的幅度减小［4］。

取起点相同窗长分别为L和2L的语音段y1（k）和y2（k），将式（18）修正为［5］

由于求和上限是L-1，与n无关，求和项数始终保持为L，自相关函数曲线不下降。

4　仿真与分析

仿真环境在MATLAB7.0下进行。通过麦克风采集10男10女20段语音信号。设带噪语音信号的长度为M，计算输入和输出信噪比的公式分别为：

将纯净语音信号分别以5dB和0dB的信噪比进行混合，仿真结果如图1、图2所示。

仿真结果表明，在5dB信噪比下，改进的算法比传统算法输出信噪比高1.9dB，0dB条件下改善1.1dB。主观听觉上也可比较出改进算法的可懂度和舒适度都高于传统算法。这是因为在分帧处理的前提下，传统自相关函数的计算方法随着n取值的增大，参与求和的项数减少，当n值较大时，估计出的自相关函数值偏差较大；而改进后算法求和项数保持L项，避免了自相关函数衰减的问题。

图1　5dB信噪比条件下的仿真结果

图2　0dB信噪比条件下的仿真结果

1 胡航.语音信号处理［M］.哈尔滨：哈尔滨工业大学出版社，2000

2 赵力.语音信号处理［M］.北京：机械工业出版社，2003

3 朱琦.采用两级维纳滤波器的消噪系统［J］.南京理工大学学报，1997， 21 （4）：306～308

4 鲍长春，樊昌信.基于归一化互相关函数的基音检测算法［J］通信学报， 1998， 19（10）：27～31

5 张雪英.数字语音处理及MATLAB仿真［M］.北京：电子工业出版社，2010

10.3969/j.issn.1006-6403.2016.06.015

（2016-05-31）