行列式的计算
于荣娟
(内蒙古农业大学,内蒙古 呼和浩特 010018)
行列式的计算
于荣娟
(内蒙古农业大学,内蒙古呼和浩特010018)
行列式的计算是求解线性方程的基础.教材上对于行列式的计算只是简单的提了一部分,本文对行列式的计算方法进行归纳总结.
行列式;线性方程组;计算方法
线性代数是以求解线性方程组为中心的一门数学分支,而行列式的计算在求解线性方程组中占有很重要的地位.但行列式的计算方法很多,综合性较强.本文根据相关资料,对行列式的计算方法归纳.
1 定义法
应用行列式的定义来计算其值的方法,称为定义法.适用于0比较多的行列式.
证明若记,λi=ai,n-i+1,则依行列式定义
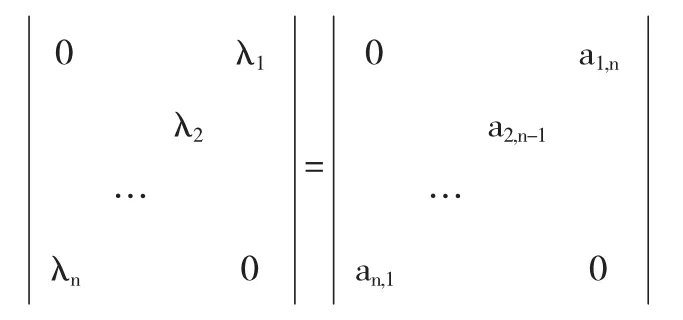
=(-1)τa1,na2,n-1…an,1=(-1)τλ1λ2…λn其中τ为排列n(n-1)…1的逆序数,故
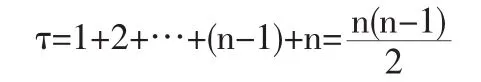
2 按行按列展开法

解按照第一列展开
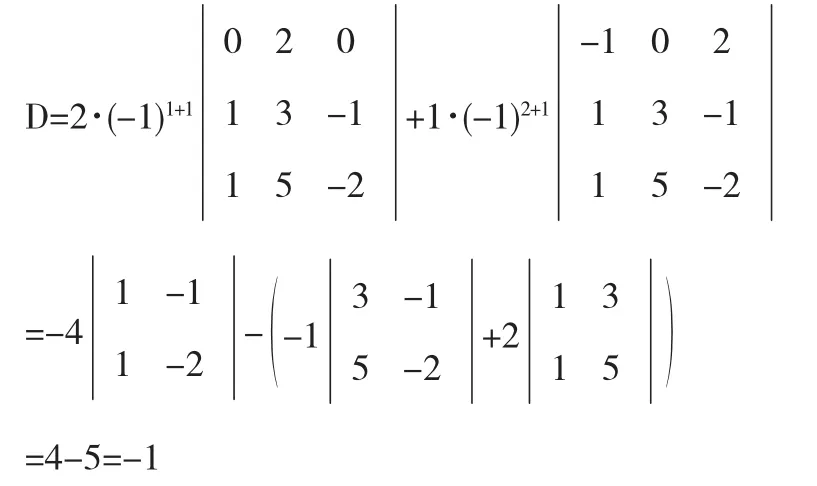
3 化三角形法
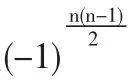
解

4 提取公因式法
若行列式满足下列条件之一,则可应用此法:某行或某列元素完全相同;某两行或某两列对应元素作和或作差完全相等;行或列元素作和之后相等.满足第一个条件的行列式可将相同元素提取出来,行列式此行都为1,通过消去变换将此行化为“1,0,…,0”型,于是应用按行(列)展开定理,使行列式降低一阶.满足条件第二个和第三个的行列式都可根据行列式的性质转化为满足第一个的行列式,继而使用提取公因式法.

5 利用范德蒙(Vandermonde)行列式法

解根据范德蒙行列式,可得
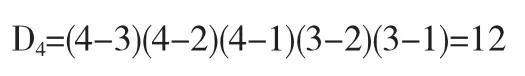
6 递推法
利用递推关系,建立同类型n阶与n-1阶(或更低阶)行列式之间的关系——递推关系式,利用递推关系式求出原行列式的值.
解将Dn的第一列视为(a-c)+c,0+c,…,0+c,据行列式的性质,得

由于b与c的对称性,不难得到

联立(1)和(2)解之,得Dn=(b-c)-1[b(a-c)n-c(a-b)n]
7 升阶法(加边法)
在计算行列式时,一般情况下先根据行列式的性质将给定行列式简化,再用展开定理使之降阶,从而使计算步骤变得简单.有时与一般方法恰恰相反,即需在原行列式的基础上添加行和列使其升阶构造一个容易计算的新行列式,然后求出原行列式的值.这种计算行列式的方法称为升阶法(有点时候也称加边法).凡可利用升阶法计算的行列式都具备特点是:除主对角线上的元素外,其余的元素都相同,或任两行(列)对应元素成比例.升阶时,根据原行列式的特点作出适当的选择.

8 拆开法
此法的具体做法是,根据行列式的形式,将行列式的某一行或某一列的元素拆成两数之和的形式,再利用行列式的性质(性质4)将行列式拆成两个新行列式的和,使问题简化便于计算.

9 利用拉普拉斯展开定理计算行列式
根据拉普拉斯展开定理可知:在行列式D中任取k(1≤k≤n)行(列),由着k行(列)元所组成的一切k阶子式分别与它们的代数余子式的乘积之和,等于行列式D.
解按1,2行展开,则不为0的2阶子式分别为
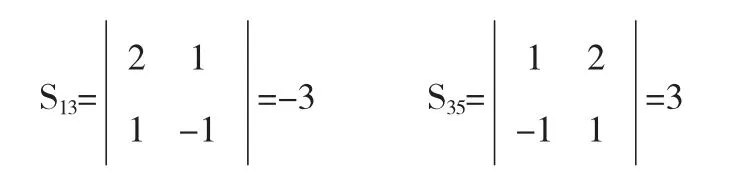
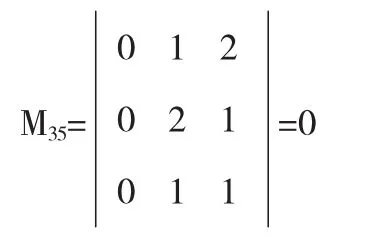
所以D=S14(-1)1+2+1+2M13+S35(-1)1+2+3+5M13=0
由上述可以看出,计算行列式有定义法、按行(列)展开、化三角法等9种方法,通过上述9道例题可以发现,选择不同的方法计算,难易繁简程度不一,所以要使计算过程简单,必须选择合适的方法,我们更需要掌握一定的解题技巧.本文,也只是总结了一部分行列式的计算,还有其他的计算方法和技巧需要我们继续探讨和归纳.
〔1〕张禾瑞,郝炳新.高等代数(第四版)[M].北京:高等教育出版社,1997.
〔2〕北京大学数学系几何与代数教研室代数小组编.高等代数(第二版)[M].北京:高等教育出版社,2003.
〔3〕徐仲,陆全,张凯院,等.高等代数(北大·第三版)导教·导学·导考[M].西安:西北工业大学出版社,2003.
〔4〕张新功.行列式的计算方法探讨[J].重庆师范大学学报:自然科学版,2011,28(4):88-92.
〔5〕李蕾.行列式的计算[J].科技资讯,2014(29):135-137.
O151
A
1673-260X(2016)04-0025-03
2015-10-22

