球面方程的不同形式及其应用
王玉光,李亚男
(1.宁夏大学 数学计算机学院,宁夏 银川 750021;2.河南理工大学 万方科技学院,河南 焦作 453000)
球面方程的不同形式及其应用
王玉光1,李亚男2
(1.宁夏大学数学计算机学院,宁夏银川750021;2.河南理工大学万方科技学院,河南焦作453000)
球面是几何学研究的重要对象,根据球面方程的不同形式,给出了其在解析几何、微分几何和数学分析等课程的理论学习及实际生活中的一些应用.
球面;方程形式;应用
球面在实际生活当中有着重要应用,也是几何学研究的一个重要对象.几何上很多著名的定理都和球面有关,著名的庞加莱猜想就是其中一个典型代表.在高校数学专业本科生的多门数学课程中,如解析几何,数学分析,微分几何,高等几何等,有很多地方都涉及到球面.所以,掌握球面的常见表示形式,知道其相互联系和区别,并灵活地加以应用,不论对学生兴趣的培养、知识的学习还是能力的提高都有积极的帮助.根据近年来承担宁夏大学数学大类相关专业几何学教学改革的实践经历,以“球面方程的常见形式及其应用”为例,介绍了课堂教学的详细过程,根据球面方程的不同形式,给出了其在解析几何、微分几何和数学分析等课程的理论学习及实际生活中的一些应用,最后提出课程教学改革的一些建议.
所谓球面,是在空间中到定点的距离等于定长的点的集合,其中定点叫做球心,定长叫做半径.为了方便,除非特别说明,否则下文所说球面都指球心在原点,半径为a的球面,所有的图形,都是在右手笛卡尔直角坐标系下而言.
1 普通方程
在空间单位直角坐标系下,球面普通方程的形式为

2 向量方程
在空间单位直角坐标系下,球面向量方程的形式为

3 参数方程
在空间单位直角坐标系下,球面的参数方程可以表示为

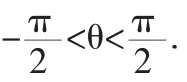
除了上述地理坐标的实际用途外,(3)中参数方程对于计算球面的面积也有方便之处.由内蕴几何知识可知,曲面域的面积由其第一基本形式完全确定,所以球面的面积
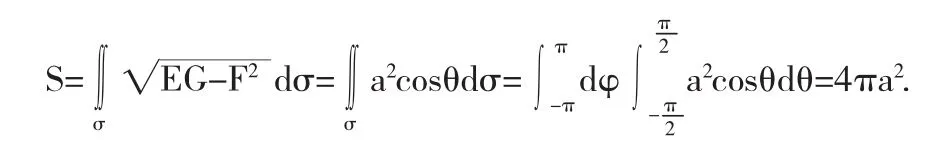
除了上面介绍的地理坐标参数表示,还有其他一些类似的表示方法,如天文学、测量学、地质学以及结晶学等中的赤道坐标系参数表示和水平坐标系参数表示.这些本质上和地理坐标参数表示是类似的,有兴趣的同学可以查阅进一步资料和文献.
4 球坐标方程
当建立了空间球坐标系后,空间任一点的直角坐标和球坐标之间有如下关系

其中参数的变化范围是ρ≥0;0≤φ≤2π;0≤ø≤π.需要注意的是,和(3)中的参数相比较,φ的几何意义相同,只是为了方便变化范围换成了[0,2π];ø则是θ的余角,即空间任一点的向径和z轴正向的夹角,同样为了方便其变化范围换成了[0,π].
在球坐标系下,球面的方程有更简洁的形式,即

仍考虑球面围成的空间立体的体积
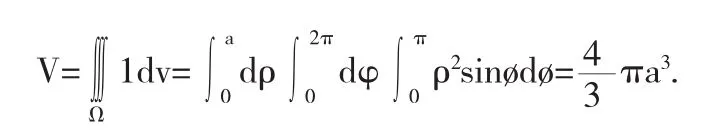
5 球极投影
球极投影也是表示球面的一种重要形式,其起源至少追溯到古希腊托勒密甚至欧多克斯时代,其思想源自光的直线传播.把球面放在一平面上,假设在球面的最高点(称为北极)有一光源,则由其发出的光穿过球面上任一点之后一定射向平面上的一点,将平面上的点作为球面上点的对应点,这就是球极投影.
显然,除北极外,球面上点和平面上的点一一对应.在直角坐标系下,球面和平面的参数方程可以分别表示为

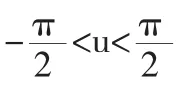
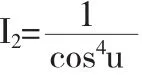
6 麦卡托投影
除了球极投影外,麦卡托投影也是将球面变换到平面的一种常见方式.仍考虑球面的参数方程(3),易知此时球面的第一基本形式为
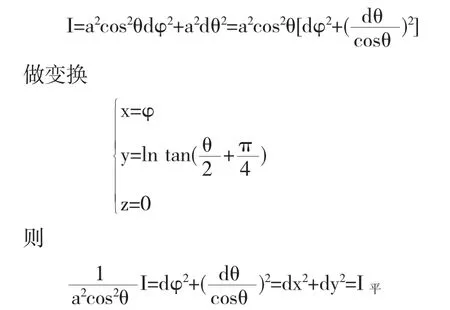
从而可以按上述变换将球面保角变换到平面上,此时变换后的图形是平面上一个带形区域
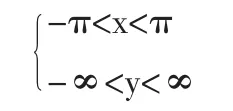
球面中的经线变成xoy平面和y轴平行的直线,球面中的纬线变成变成xoy平面和x轴平行的直线段,这也是通常世界地图的一种制作原理.16世纪麦卡托首先用这种方法,所以一般也称作麦卡托投影.
然而需要说明的是,尽管麦卡托投影可以用来制作世界地图,但是该投影也并不是将球面变换到平面上一个有界区域,而是对极点附近也做了模糊处理.比较麦卡托投影和球极投影可以发现,相同之处是两者都是球面到平面的保角变换,不同之处主要在于前者将球面变到平面一带形区域,后者将球面变到平面一上下左右都无界的区域.而且易知,这两种变换后的图形之所以无界主要是由于极点附近的点所致.由此可见,在上述两个对应下,极点及附近的点可能是一些性质比较“坏”的点.
既然球极投影和麦卡托投影都不能将球面变换到平面上一个有界区域内,那么,能不能找到一个变换能将球面变换到平面上一个有界区域内?答案是否定的.这是因为三维空间的可展曲面只有柱面、锥面和空间曲线的切线曲面这三类曲面,或者说只有高斯曲率恒为0的曲面.而球面的高斯曲率为正常数,从而不可展,更不必说展开到平面上的一个有界区域了.
〔1〕吕林根,许子道.解析几何(第四版)[M].北京:高等教育出版社,2009.
〔2〕梅向明,黄敬之.微分几何(第三版)[M].北京:高等教育出版社,2003.
〔3〕宋鸿藻,等.微分几何及其应用[M].开封:河南大学出版社,1994.
〔4〕张奠宙,沈文选.中学几何研究[M].北京:高等教育出版社,2006.
O18
A
1673-260X(2016)04-0009-02
2015-10-13
宁夏大学科学研究基金(ZR1414)

