参数型拉格朗日插值公式
刘国祥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
参数型拉格朗日插值公式
刘国祥
(赤峰学院数学与统计学院,内蒙古赤峰024000)
本文给出经过n+1个定点的参数式平面曲线和空间曲线的拉格朗日型插值公式,这些点的横坐标可以重复,甚至有些点是可以重复的.
平面曲线方程;空间曲线方程;参数方程;拉格朗日插值公式
给定平面上的n+1个不同的点

如果他们的横坐标xi(i=0,1,2,3,……,n)任意两个互不相同,当然我们不妨假定x0<x1<x2<……<xn.那么,一定存在唯一的次数不超过n次的多项式Pn(x),使得满足条件:yi=Pn(xi),(i=0,1,2,3,……,n).这个多项式用拉格朗日型插值公式表示是:

例如,当n=2时,直接写出来是:

这里必需注意的是,他们的横坐标xi(i=0,1,2,3,……,n)互不相同.如果横坐标相同,不可以写出这样的多项式,因为多项式是单支函数,同一个横坐标xi对应的函数值yi必须是唯一的.现在我们要考虑的是,如果他们的横坐标xi(i=0,1,2,3,……,n)有重复,更甚至点集合(xi,yi),(i=0,1,2,3,……,n)有重复,是不是能够找到通过这n+1个点的曲线呢?
注意,这里用“曲线”,当然可以用方程,但是绝不是函数,绝不是多项式.
考虑到参数方程和极坐标方程可以表示更多的曲线,但是极坐标不容易推广到三维立体空间中,尝试借助于参数方程,参照拉格朗日插值公式,能够做到这一点.先就简单的例子说明方法,再推广到一般情形.
例1求经过(0,0),(0,1),(1,0)三点的曲线的参数方程.
解这里横坐标有重复的,不能够直接应用拉格朗日插值公式.因为经过三个点,试图引进一个参数t,t取值为0,1,2.做两个以t为参数的函数x=x(t),y=y(t),t=0,1,2.使得:

应用拉格朗日插值公式,得到经过(0,0),(0,1),(1,0)三点的曲线的参数方程:

化简后得到:

这个参数方程,在t=0,1,2时,分别得到(0,0)(0,1),(1,0)三个点.所以它是经过三个已知点的参数曲线方程.
利用Matlab画出曲线的图形,看的更清晰.

图1 经过(0,0),(0,1),(1,0)三点参数的曲线
把这个简单的例子作为一般性的推广,就得到平面上或者空间中通过n+1个点(坐标可以重复)的拉格朗日型插值参数方程.
定理1通过平面上的n+1个点:(x0,y0),(x1,y1),(x2,y2),……,(xn,yn)的拉格朗日型参数方程是:

定理2通过三维立体空间中的n+1个点:(x0,y0,z0),(x1,y1,z1),(x2,y2,z2),……,(xn,yn,zn)的拉格朗日型参数方程是:

例2 求通过4个定点:(1,0),(-1,0),(0,1),(0,-1)的平面参数曲线方程.
解直接代入(6)式中:

容易看出来,题目所给定的4个点在单位圆周x2+y2=1上,但是这个参数方程消去参数并不是这个圆,有一点象笛卡尔曲线的样子.
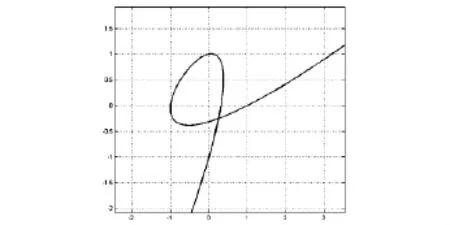
图2 经过(1,0),(-1,0),(0,1),(0,-1)四点的参数曲线
例3求通过5个定点:(1,0),(-1,0),(0,1),(0,-1),(1,0)的平面参数曲线方程.
解这里的(1,0)点,是第一个点,也是第五个点,也就是说有重复点,应该就是曲线的一个重点.
直接代入(6)式中:

化简后得到:

容易看出来,虽然经过的点一样,这里的曲线与例2是有区别的,除了(1,0)点外,还有一个重点.

图3 通过(1,0),(-1,0),(0,1),(0,-1),(1,0)五点的平面参数曲线
例4求通过3个定点:(1,0,0),(0,1,0),(0,0,1)的空间参数曲线方程.
解直接代入(7)式中:

这里参数t的取值为0,1,2,……n,如果取其他值,类似的可以得到其它形式的参数方程.

图4 通过(1,0,0),(0,1,0),(0,0,1)三点的空间参数曲线
〔1〕许萃薇,孙绳武.计算方法引论[M].北京;高等教育出版社,2002.30-31.
〔2〕刘国祥.用插值方法得到的几个恒等式[J].赤峰学院学报,2005,8(4):28-31.
〔3〕刘国祥,用插值方法构造多项式证明中值问题[J].赤峰学院学报,2011,3(3).
〔4〕刘国祥.收敛速度阶数更高的迭代开方公式[J].赤峰学院学报,2011,2(2).
〔5〕武汉大学,山东大学.计算方法[M].北京;高等教育出版社,1983.
O122.4
A
1673-260X(2016)04-0021-02
2015-12-29

