高等代数与解析几何课程教学现状分析及其提高教学质量的途径

余柏林



高等代数与解析几何课程教学现状分析及其提高教学质量的途径

余柏林

（淮阴工学院 数理学院，江苏 淮安 223003）

以在高等代数与解析几何课程实践教学中积累的经验为基础，结合对该课程教学现状的问卷调查与分析，针对当前出现的普遍问题提出相应的改进措施，为提高高等代数与解析几何课程教学质量提供参考．

高等代数与解析几何；教学现状；教学质量

随着我国高等教育改革，尤其是课程教学改革的不断深入和发展，如何让学生在相同或更少的时间内学会更多的知识，培养成素质高、能力强的复合创新型人才，已成为当前课程改革的核心问题．作为数学专业学生的传统课程，高等代数和解析几何互为方法、相互交融．随着理工科院校新课程的开设及其学时的增加，分别开设高等代数和解析几何2门课程无疑将占用较多课时．因此，将高等代数和解析几何2门课程合并为1门课程进行教学是非常必要的．这也得到了陈省身、杨忠道和王叔平等数学家的倡导．南开大学孟道骥教授的专著《高等代数与解析几何》[1]一书于1998年率先出版．而后，华东师范大学的陈志杰教授编著的《高等代数与解析几何》等一系列将高等代数和解析几何2门课程合并为1门的教材[2-3]相继出版．将高等代数和解析几何2门课程合并进行一体化教学，不仅能节省出许多的学时，而且不会削减过多的教学内容．从某种意义上说，反而使这2门课程得到加强．但在实际的教学过程中，由于代数与几何合并教学的特点，教师教学水平和学生学习能力等方面的原因，高等代数与解析几何课的教学质量不尽如人意，出现教学效果不好，学生不愿意学的局面，难以实现培养学生数学能力的目的．本文以在高等代数与解析几何课实践教学中积累的经验为基础，结合对该课程教学现状的问卷调查与分析，针对当前出现的普遍问题提出相应的改进措施，为提高高等代数与解析几何课程教学质量提供参考．

1 高等代数与解析几何课程教学现状

为全面把握高等代数与解析几何课程教学现状，充分了解学生在学习本门课程时所面临的困难，设计了包含对本课程的整体认识、障碍大小程度、概念理解、性质推导、定理证明、知识的应用及习题的完成等方面在内的问卷调查表．本次调查的对象从信息与计算科学专业各年级学生中选出，共计70名学生.

在对课程整体认识方面，约13％的学生认为高等代数与解析几何课程非常难学，约82％的学生认为难学，对本门课程不感兴趣和很不感兴趣．有如此多的学生认为本课程难学和不感兴趣，是教学中所不曾设想到的．为了解学生认为本课程难学和不感兴趣的原因，在调查表中设计了让学生按学习困难的大小程度进行排序，结果见表1．

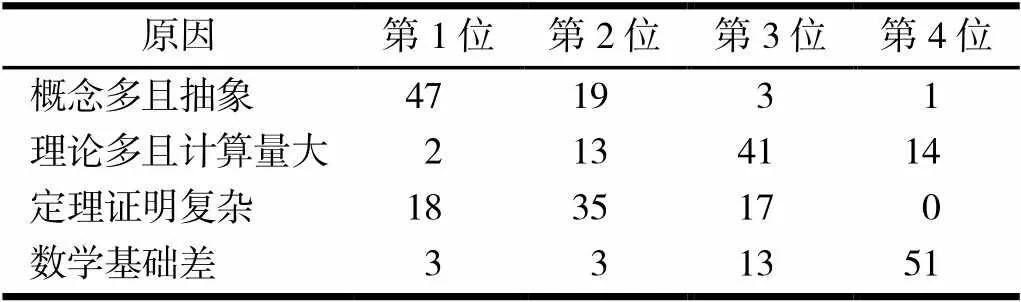
表1　学习困难原因

注：表中数字代表学生人数．

由表1可以看出，约67％的学生认为本课程的概念多，概念多且抽象是学生认为本课程难学和不感兴趣的第1位原因，而约27%的学生认为概念多且抽象应是本课程难学的第2位原因；约58％的学生认为本课程的理论多且计算量大是本课程难学的第3位原因；50％的学生认为本课程的定理证明过于复杂是本课程难学的第2位原因，而认为定理证明过于复杂是第1位原因和第3位原因的分别约占26％和24％；约73％的学生认为自身数学基础差是本课程难学的第4位原因．可以得出，绝大多数学生认为本课程学习困难的大小程度顺序为：概念多且抽象、理论多且计算量大、定理证明复杂、自身的数学基础差．

通过调查，发现只有21％的学生基本能理解高等代数与解析几何课程中的抽象概念，而大多数学生（占73％）对本课程中数学概念都是似懂非懂，没有形成自己对概念的认识；大约有70％的学生分别对性质推导、定理证明过程的理解是似懂非懂，在课后则不能独立、完整、正确地完成相关作业．在对似懂非懂地理解数学概念的这部分学生进行的调查中，发现大约21.4%的学生是由于跟不上教学进度，导致部分内容前后衔接不上问题；有14.3%的学生根本不懂，不明白所讲概念是怎么回事．余下的64.3%的学生则是对相关数学概念形成不了整体认识，没有自己的理解和体会．

对不能独立完整地完成相关作业的这部分学生进行调查，发现大约54.3%的学生是缺乏明确的求解问题思路，不能完整解决问题；45.7%的学生根本找不到问题的求解思路．

从问卷调查情况看，在本课程的学习中，大多数学生在数学抽象概念、理论性质推导．定理证明的理解、掌握以及灵活运用上都有很大困难．这些困难应排在导致本课程难学成因的第1位到第3位，也是学生学习中存在的最主要困难．

2 成因分析

通过对学习困难原因分析，归纳起来主要有3个层面：高等代数和解析几何课程自身的特点，教师的“教”和学生的“学”．

2.1高等代数与解析几何课程自身的特点

虽然高等代数与解析几何课程的部分研究对象比较具体，如多项式理论、行列式、线性方程组、矩阵和二次型等，但是本门课程的数学概念非常多，学生往往搞不清楚这些数学概念之间的关系．如学生很容易混淆矩阵的等价、相似和合同等概念，不能明确这些概念之间的区别与联系．

课程教学内容非常抽象．形式化、符号化及公理化是本课程中相关数学概念的显著特点．如线性空间，线性相关与线性无关，线性子空间的直和、同构，线性变换，线性空间同构与对偶空间，内积空间等概念．教材上，这些理论的组织基本上是从理论到理论，从符号到符号，缺少具体直观的数学或物理模型．本课程现行教材这种“重理论、轻应用”，“重公式推导、轻数值计算”的特点，不符合信息与计算科学专业的办学特色与人才培养目标．学生缺乏对相关概念的感性认知和其应用背景的了解．因此，对概念的理解、性质推导和定理的证明出现一知半解、似懂非懂的现象也就不足为怪了．

课程计算量大，理论证明复杂，对学生思维水平的要求高．如求矩阵的特征值与特征向量以及矩阵的Jordan标准形及其相应的变换矩阵等的计算工作量是很大的，而且这些工作都是程序化的．若总是让学生手工计算，久而久之学生就会失去对本门课程的学习兴趣、热情和学好它的自信心．

2.2教师的“教”

与其它大学数学课程的教学一样，高等代数与解析几何课程的教学由3部分构成：课堂讲授、习题（课堂练习题和课外作业）和考试（期中和期末等考试形式）．教师课堂讲授时，主要包括概念的介绍、基本性质的推导、重要定理的证明、例题及课堂练习题的讲解．这种传统教学模式的基本形态就是：定义→性质→证明→定理→证明→例题→作业→考试．此外，这种教学模式过于强调教师的中心地位，而弱化了学生的主体地位，没有充分地让学生参与到整个教学过程中来．高等代数与解析几何课程的教学要求和目标就是在传授知识的同时，既要培养学生的抽象思维能力、逻辑推理能力和空间想像能力，又要特别注意培养学生运用所学知识去分析问题和解决问题的能力．对于面向信息与计算科学专业学生而设置的高等代数与解析几何课程若单纯地采用传统教学模式，是难以产生师生互动的教学氛围，难以提高课堂教学质量，更难以达到本课程的教学要求目标．

此外，由于一些新学科的设置，本课程的教学学时一少再少（2学期，共128学时）．这就造成教师在课堂讲授时，只能把有限的、紧张的时间用于定义、定理、例题和部分练习题的讲解上，而无法顾忌相关概念的来源、定理的应用背景等介绍，更没有时间去考虑利用计算机技术来进行可视化教学和相关数学实验．这种一维式的教学模式（即“定义→性质→证明→定理→证明→例题→作业→考试”）主导下教学，缺少具体直观的数学或物理模型，不能有效地引导学生主动学习，不能充分提高学生的学习热情和积极性，也就不能取得良好的教学效果．

2.3学生的“学”

为了解学生在学习高等代数与解析几何课程时的学习现状，进一步分析本课程的学习困难成因，分别对学生在课前准备、课堂听课情况、课后复习及作业完成等方面进行调查．

2.3.1课前准备情况从课程辅导资料阅读情况（见表2）可以看出，只有7.1%的学生在课前阅读过本课程的相关教学辅导资料，52.9%的学生从来没有阅读过本课程的相关教学辅导资料．在课前预习方面，57.1%的学生从不预习，42.9%的学生只是偶尔预习一下，而坚持预习的学生一个也没有．据此，可以明确：在学习高等代数与解析几何课程时，绝大多数学生对本课程认识不够，甚至根本不重视，学习缺乏积极性和主动性．这部分学生只是简单地、被动地、消极地学习．

表2　学生课前准备情况 %

2.3.2课堂听课情况调查发现，70.0%的学生把主要精力和时间放在解题思想及方法上，重在如何计算．只有17.1%的学生把听课重点放在基本概念上，关注概念的提出背景、发生过程．此外，约有13%的学生重在定理或性质的推导过程及其技巧掌握方面．

2.3.3课后复习及作业完成情况调查发现，只有10.0%的学生坚持课后复习，养成了良好的复习习惯．而分别有72.9%和17.1%的学生偶尔复习和根本没有复习．在课后作业的完成方面，能独立完成作业的学生和抄袭别人作业的学生都分别占7.1%，大半学生都需要查看笔记和教辅资料，或者与同学讨论后才能完成．只有1个学生从来不做作业．此处，还有34.3%的学生只是偶尔做一点作业，没有养成按时完成作业，上交作业的习惯．

可以看出，无论是课前还是课后方面，很多学生对高等代数与解析几何课程的重要性认识不够，学习兴趣不浓，缺乏学习的积极性和主动性，处于消极学习和为考试而学习的状态中．本课程所面向的教学对象是刚进入大学生活的大一新生和入学不久的大二学生，很多学生还没有从中学形成的学习方法、学习习惯过渡到大学的学习中来，受应试教育的影响，还是只注重解题方法与技巧方面，而忽视对数学概念本质的理解．这些学生的数学思维能力和认知水平不高，对形式化、符号化的定义方式比较陌生，仅凭对中学数学课程的认识是很难学习课程中那些抽象的数学概念和复杂的理论．如学生对线性空间、线性变换、内积空间以及同构等概念非常不理解，甚至不明白为什么要学这些抽象概念．此外，这些刚入校园不久的学生独立思考能力不高，在解题方面只会套公式，不能灵活运用．这也导致他们学习本课程存在一定的困难．

3 提高高等代数与解析几何课教学质量的途径

基于高等代数与解析几何课程自身的特点和学生学习本课程时所面临的困难及其成因分析，欲实现本课程的教学要求和目标，就必须改变传统的教学模式，把以教师为中心改变为以学生为中心，以教师为主导，让学生直接参与到整个教学过程中；不断调查研究，探索更加适用于本课程教学的新教学方法．如基于项目和问题的研究性教学[4-5]、案例教学[6]和可视化教学[7-9]等．在教学过程中，尤其要注意以下2个方面．

3.1加强本课程抽象概念的教学

本课程教学内容非常抽象．形式化、符号化及公理化是本课程中相关数学概念的显著特点．如何将抽象的概念具体化、直观化，实现数形结合，使学生更容易理解并接受，是课程教学中急需思考的一个问题．

3.1.1 从低维空间过渡到高维空间在讲授概念时，首先在二维或三维实空间（或）考虑，然后再推广到一般的维实空间，最后再抽象到一般维线性空间．这样做符合学生的认知规律，即直观到抽象，低维到高维；也降低了相关概念的抽象性，使学生更容易理解和掌握本课程中的概念，加深了学生对所学知识的认识．

3.1.2利用数学概念的几何或应用背景，强化学生对概念理解课程中有很多数学概念抽象难懂，但这些概念往往具有其相应的几何或应用背景．如三维空间中向量组线性相关问题的几何背景就是该向量组共面问题．三阶行列式在几何上就是一平行六面体的体积问题（符号右手法则）．在讲授初等矩阵概念时，若能通过一些应用型问题的举例，让学生体会到利用伴随矩阵求逆的困难，进而体会到初等行（列）变换的妙用时，引入初等矩阵的概念，学生就容易接受，学习效果自然会好．总之，这种注重数学概念本身的几何背景或在现实生活的应用背景的教学，是理论联系实际的最好表现．尤其是通过来自实际的真实问题介绍，有利于激发学生的学习热情，培养学习兴趣，提高其分析问题和解决问题的能力．

3.1.3注重类比教学，厘清概念内在联系高等代数与解析几何课程的教学内容非常丰富，所涉及到的数学概念也非常多．在初学本课程时，学生往往因搞不清这些数学概念之间的关系而感到迷惑．通过对相关数学概念进行类比，可以厘清概念内在联系，使学生思路清晰，更容易接受所授知识，进而加深对概念的理解．以矩阵等价、相似、合同的概念为例，通过对类比教学，可让学生清楚：.相似必等价，合同必等价；等价不一定合同，等价也不一定相似；相似不一定合同，合同也不一定相似．

3.2教学过程中充分运用可视化技术

可视化作为专业术语的出现，始于上世纪90年代的美国．随着计算机技术的发展，可视化已经广泛地应用于各个领域中．计算机可视化技术也为教学提供了形象生动的图形，减少用于手工计算的时间，缩短了课程与学生的距离，有助于学生理解抽象的数学概念，增强学生的数学能力．

以求矩阵的特征值与特征向量为例，探索如何利用计算机代数系统Maple[10]软件来进行可视化教学．与以往其它文献不同的是，本文着重于在教学过程中一步一步地演示计算的过程和理论的推导，而不是仅仅局限于得到计算的结果和图形的描绘．

特征值与特征向量是一类非常重要的概念．会求矩阵的特征值与特征向量，是本课程教学的基本要求之一，它也是学习本课程后续教学内容（如对角化问题和Jordan标准形等）以及其它课程的一个必备的数学基础．在讲授这一知识点时，教师在阐述矩阵的特征值与特征向量求解方法后，往往手工演示一二个例子，然后由学自己动手做几个练习题．这样不仅占用了本来就非常紧张的教学时间，而且若总是这样手工计算，学生会感觉课程非常枯燥，当然也没有兴趣和热情学习本门课程．利用Maple软件来进行特征值与特征向量的可视化教学，就可避免上述问题，达到事半功倍的效果．

若只需要求矩阵特征值与特征向量的结果，则可以直接利用Maple软件提供的Linear Algebra软件包，进行以下操作即可：

>With（LinearAlgebra）：

>A：=输入的矩阵；

>Eigenvalues（A）；

>Eigenvectors（A）；

但是若要向学生演示矩阵特征值与特征向量的求解步骤，则可利用Maple软件提供的向导功能菜单．首先点击主窗口工具（Tool），在下拉菜单中选中向导，然后选中线性代数子菜单，最后在该下拉菜单中分别选择特征值和特征向量子菜单．弹出交互式窗口界面（见图1）．

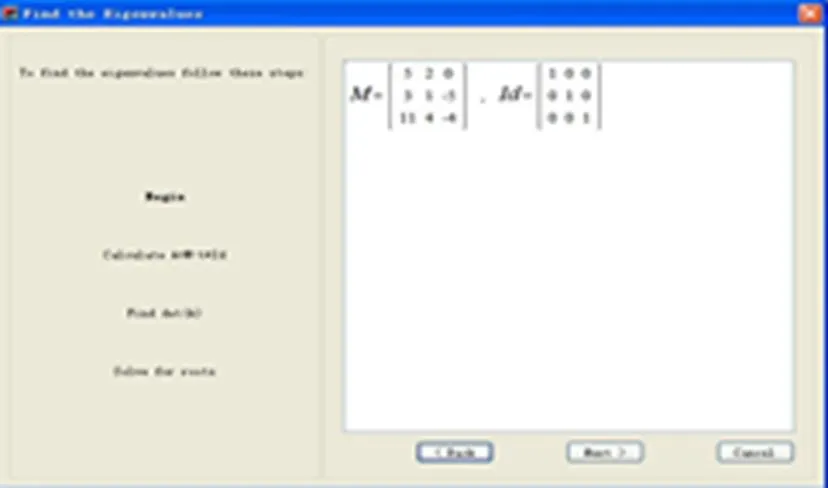
图1　计算特征值

点击“Next”按钮，则有计算特征值第１步：计算特征矩阵（见图2）．然后再点击“Next”按钮，则出现计算特征值第２步：计算特征多项式（见图3）．最后，点击“Next”按钮则可得特征根（见图4）．

图2　计算特征矩阵

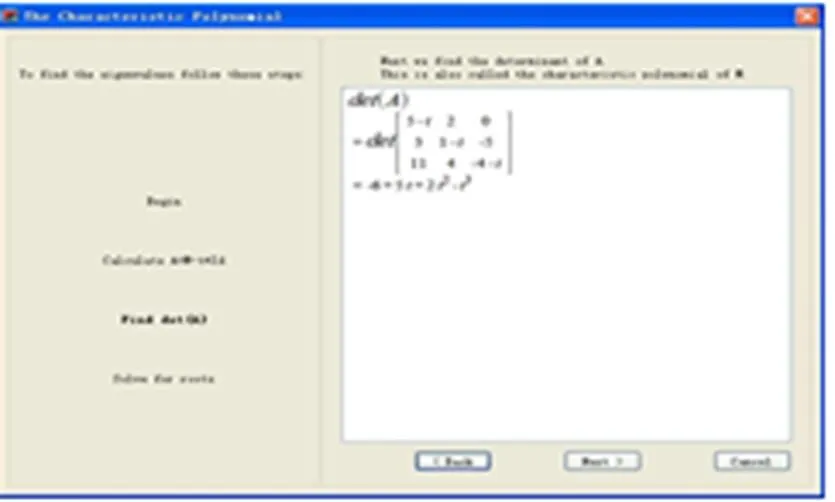
图3 计算特征多项式

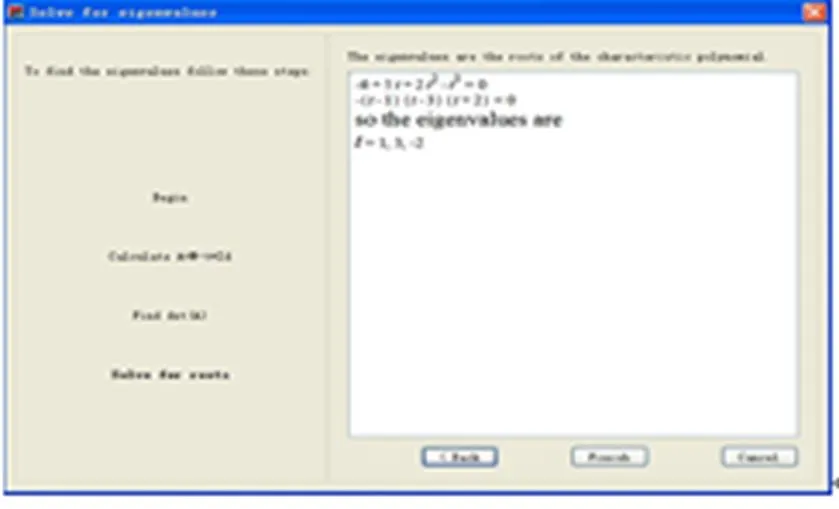
图4 求解特征方程的根

类似地，通过工具→向导→线性代数→特征向量进入主界面窗口，也可以用Maple软件来解相应的特征向量．由于计算机代数系统Maple软件所得到的结果是精确的符号解，这与Matlab等其它偏重于数值计算的数学软件不同，这正是高等代数与解析几何课程中性质推导和定理证明相关教学演示所需要的．由此可见，通过对矩阵求特征值与特征向量过程的展示，既减轻教师的负担，又让学生直观地体会了求特征值与特征向量的方法，加深他们的认识，也非常有利于提高学生的学习兴趣，有效提高了教学效果．

通过对高等代数与解析几何课程教学现状的调查和分析，得出导致学生学习困难主要受课程自身特点、教师的“教”和学生的“学”等方面的影响，并据此提出提高教学质量的途径．若能与传统教学方相互结合、相互补充，这些教学方法和策略可有效应用于本课程的教学过程中．这也是对传统教学方法的一种有益的改革尝试．

[1] 孟道骥．高等代数与解析几何[M]．北京：科学出版社，1998

[2] 陈志杰．高等代数与解析几何[M]．北京：高等教育出版社，2000

[3] 同济大学应用数学系．高等代数与解析几何[M]．北京：高等教育出版社，2005

[4] 李尚志．从问题出发引入线性代数概念[J]．数学学习，2006，9（5）：6-8，15

[5] 陈建华，李立斌，凌智．基于问题解决的线性代数课程教学设计研究[J]．高等理科教育，2011（4）：117-119， 152

[6] 赵思林，朱德全．试论数学直觉思维的培养策略[J]．数学教育学报，2010，19（1）：23-26

[7] 郑秀琴，杨晓春．Matlab在数学教学中的可视化研究[J]．高师理科学刊，2006，26（3）：102-104

[8] 王小华．基于Mathematica的高等数学教学实践[J]．重庆科技学院学报：自然科学版，2010，12（4）：195-198

[9] 李世贵，李青，杨天国．可视化教学与数学能力培养[J]．重庆科技学院学报：社会科学版，2006，（1）：124-126

[10] 刘辉，李海．Maple符号处理及应用[M]．北京：国防工业出版社，2001

Teaching strategies to enhancd the quality of course teaching based on the analysis on the current teaching situation about higher algebra and analytic geometry

YU Bo-lin

（School of Mathematics and Physics，Huaiyin Institute of Technology，Huaian 223003，China）

Based on an detailed analysis on a questionnaire about the course of higher algebra and analytic geometry and our practical teaching experiences，proposed some teaching strategies and methods that can be applied effectively into our practical teaching process in order to enhance our quality of course teaching.

higher algebra and analytic geometry；current teaching situation；teaching quality

1007-9831（2016）07-0070-06

O1∶G642.0

A

10.3969/j.issn.1007-9831.2016.07.019

2016-04-09

余柏林（1979-），男，四川广安人，副教授，博士，从事组合矩阵理论及应用研究．E-mail：berlinyu@163.com