有限质量降落伞充气动力学数值模拟*

高兴龙，张青斌，高庆玉，唐乾刚，杨　涛

(1. 国防科技大学 航天科学与工程学院， 湖南 长沙　410073;2. 中国空气动力研究与发展中心 设备设计及测试技术研究所， 四川 绵阳　621000)



有限质量降落伞充气动力学数值模拟*

高兴龙1,2，张青斌1，高庆玉1，唐乾刚1，杨涛1

(1. 国防科技大学 航天科学与工程学院， 湖南 长沙410073;2. 中国空气动力研究与发展中心 设备设计及测试技术研究所， 四川 绵阳621000)

为研究空投任务中降落伞有限质量充气过程的动力学行为，基于罚函数耦合方法和网格自适应技术分析了降落伞柔性结构与周围不可压缩流场的流固耦合特性。数值模拟开伞过程伞衣三维外形变化，获得降落伞系统下落速度、阻力面积等参数；对比分析初始投放速度对降落伞开伞时间、伞衣阻力面积的影响；通过试验数据对比分析开伞力变化。计算结果表明，该方法可以有效模拟降落伞系统有限质量充气过程的动力学特性，仿真结果与试验结果相符。

降落伞；流固耦合；有限质量充气；ALE动网格

降落伞部件主要为柔性多体结构，其充气过程涉及流体结构相互作用下的大变形问题，通常可借助风洞及地面空投等试验手段进行研究，同时也可结合经验公式及数值仿真的方法模拟预测降落伞开伞过程。根据降落伞周围流场的气动特性，可以将充气过程分为有限质量充气和无限质量充气：风洞试验中来流速度不发生变化，降落伞周围为稳态流场，此过程通常称为无限质量充气；相对而言，地面空投或伞塔试验则更贴近真实的降落伞开伞情况，充气过程流入伞衣的气流的速度急剧变化，流场为非稳态，通常称为有限质量充气，其流固耦合模型与降落伞系统弹道方程相耦合，求解难度较大[1]。

Wolf曾基于试验数据建立了简化的降落伞飞行过程充气模型，但并未考虑流固耦合行为，主要分析了伞衣惯性效应对充气时间的影响[2]。相比之下，Potvin等建立的充气经验模型则更真实地预测了降落伞充气行为，但其需要借助试验手段获取较准确的过载系数变化曲线[3]。Tezduyar等基于DSD/SST(deformable-spatial-domain/stabilized space-time)有限元方法对Navier-Stokes(N-S)方程进行求解，充分研究了降落伞建模和3D充气过程的流固耦合行为[4-5]。Li等采用界面追踪法(front tracking method)和弹簧系统模拟了降落伞开伞过程[6]，但并未对充气时间等性能参数进行研究。Tutt等基于ALE(arbitrary Lagrangian Euler)方法对稳态下落过程的降落伞有限质量充气进行了研究[7]。近年来，国内对于降落伞充气过程流固耦合行为进行了机理研究：彭勇等针对返回着陆任务中降落伞下落过程的充气行为进行了理论建模和求解，获得了二维有限质量情况的降落伞几何外形和流场变化[8]；程涵等针对降落伞三维的有限质量充气进行了数值模拟[9]，但需要流场网格覆盖整个飞行区域，计算量过大，较难满足实际工程需求。

本文基于ALE方法和动网格技术，以平面纵向开缝伞为例，为预测降落伞有限质量充气过程的流固耦合动力学行为和开伞性能，开展了低速空投过程的有限质量开伞过程三维数值仿真研究。模拟了伞衣充气过程的3D外形变化，对比分析主要开伞参数曲线，计算结果与试验数据一致。

1　问题描述和模型假设

所研究的降落伞系统为低空救生用伞，伞衣为平面圆形伞，并采用纵向开缝技术，伞衣表面布置加强带将降落伞对称划分为8个扇形幅，共有28根伞绳连接伞衣与挂重，降落伞伞衣平面结构模型如图1所示。降落伞结构的主要设计参数如表1所示。

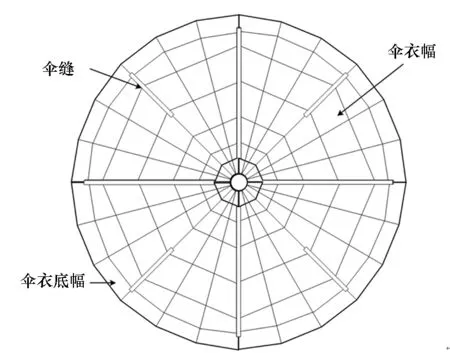
图1　伞衣平面结构模型Fig.1　Flat layout of canopy model

项目数值名义直径7.86m伞绳长度6m顶孔直径0.3m伞缝数量8

考虑降落伞动力学模型的复杂性，建模前需要进行如下假设：

1)降落伞为轴对称结构，伞衣初始为拉直状态，初始下落速度即为伞衣拉直速度；

2)降落伞系统下落过程为有倾角再入情况；

3)挂重为假人模型，模拟空投人员，忽略物伞相对运动的影响；

4)忽略伞衣织物预应力和织物摩擦对结构力学行为的影响；

5)由于降落伞是在低海拔区域做低速投放运动，忽略空气的压缩性，流场本质具有时变非稳态的气动特性。

2　动力学方程

2.1流场控制方程

考虑降落伞充气过程为低速，认为温度变化较小，故不进行能量方程的求解[10]。流场为非稳态，令Ωf为空间域，则不可压缩流场的N-S方程可以写为：

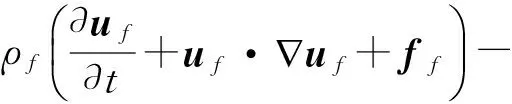
(1)

·uf=0 onΩf

(2)

其中，ρf，uf,ff和σf分别为流体密度、速度矢量、所受的外部力及应力张量。引入ALE格式，流体域和材料域网格可以自由移动，式(1)可写为：

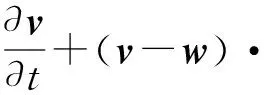
(3)

其中流体速度uf=v-w，v和w分别为流体网格和材料网格速度矢量，从式(3)可以看出，ALE格式同时包含了欧拉和拉格朗日格式[11]。

对于牛顿流体，应力张量σf定义为：

σf=-pI+μf[v+(v)T]

(4)

式中，p为压力，I为单位张量，μf为流体动力黏性系数，利用Dirichlet和Neumann边界条件可以对流体动量方程进行求解[12]。

2.2结构控制方程

充气过程降落伞结构变化通常为大变形，且伞衣和伞绳等部件均为柔性体。为避免结构过度变形所带来的单元畸变而引起计算困难，采用Lagrange描述结构域动力学方程。令Ωs为空间域，∂Ωs代表固体域边界，则结构域控制方程为：

(5)

式中，ρs为材料密度，u是位移矢量，fs是作用在结构上的体积力，σs为Cauchy应力张量。初始条件和边界条件为：

(6)

同时考虑降落伞结构的典型非线性特性，分别对伞衣薄膜单元和伞绳单元的材料模型进行二次开发，建立新的材料本构关系模型。其中伞衣薄膜单元基于传统的用于气囊充气的织物连续性材料模型，可以描述织物的屈曲和褶皱行为。

通过对应变率张量的时间积分，可以输出应力和应变值。其中自旋张量和应变张量分别为：

(7)

(8)

如果对n到n+1时间步的应变进行积分更新，则：

(9)

其中，

(10)

对于壳单元，分别在内部和外部的积分点对应变张量进行积分，并输出每个单元的两个应变张量值，最终输出中面应力作为平均值。

F=K·max(Δl,0)

(11)

Δl=l-(l0-loff)

(12)

其中，Δl为绳长变化量，材料刚度K定义为

(13)

l为绳索当前长度，E为绳索弹性模量，A为绳索截面积，l0为原长，loff为偏移量，如绳索初始状态松弛，偏移量应设为负值，若绳索受拉力，为张紧状态，偏移量应设为正值。

考虑阻尼项和非线性项的本构关系则为：

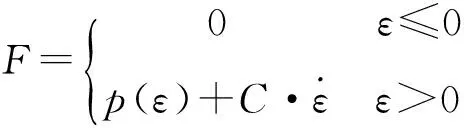
(14)

式中：p(ε)为伞绳的非线性张力函数；C为阻尼系数；应变ε为：

(15)

3　ALE耦合方法及动网格技术

3.1耦合信息传递

降落伞有限质量充气过程不仅涉及流体与结构的紧耦合，同时与降落伞系统飞行过程的弹道方程也具有紧密关系，需要根据流固耦合方程所求解的速度信息，更新降落伞下落位置信息，其中关键是流体与结构耦合界面上的节点力和节点速度等耦合信息的求解。

基于罚函数法的思想，利用流体与结构节点之间的接触特性，将穿透深度d作为惩罚因子，在每一显式积分时间步内求解流体与结构节点的相对速度并进行更新[13]。如图2所示，实心为流体节点，空心为伞衣单元的结构节点。

张宗登博士的专著《潇湘竹韵——湖南民间竹器的设计文化研究》，是张博士近年最新研究成果的总结。该书以湖南民间竹器为研究对象，以文化为研究背景，以设计为研究视角，从设计的角度剖析湖南民间竹器的一般性设计规律，从地域文化的角度分析湖南民间竹器的设计内涵与设计文化，进而构建湖南民间竹器的设计文化体系。

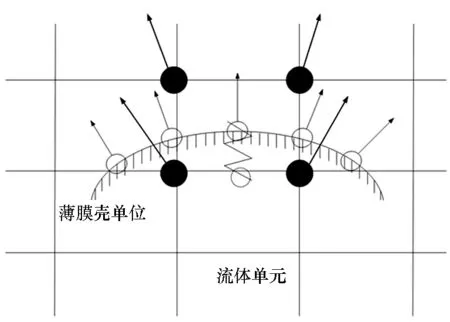
图2　流固耦合界面的罚函数法Fig.2　Penalty method of fluid-structure interaction interface

3.2ALE动网格自适应技术

实际仿真过程很难令流场求解域网格完全覆盖降落伞的飞行轨迹。考虑伞衣的变形行为主要受附近流体的影响，因此计算域网格仅选取降落伞附近的区域，同时令网格域跟随弹体系进行空间运动，则流体域同结构域仍处于相对静止状态。

具体的运动策略为：选取投物质心所在的体坐标系作为ALE动参考系，三个方向分别满足右手法则，即网格平动以投物一阶运动(质心位置)为参考，转动以投物二阶运动(质心速度方向)为参考，这样流场计算域便始终跟随投物空间运动且轴线方向与投物运动方向保持一致。

在ALE网格跟随降落伞投物系统做刚体运动的同时，还需要进行拉伸和缩放。网格的拉伸缩放以降落伞系统质心为中心节点，通过获取ALE网格的运动信息可以知道网格质心Xc的位置和速度。

(16)

(17)

其中：mi(i=[1,nn])是ALE网格节点的质量；(u，v，w)分别为节点在x，y，z方向的速度。

这样通过实时获得流固耦合计算中所得到的结构运动信息，就可以引导流体网格进行跟随求解。

4　仿真模型

所计算的有限质量充气过程指降落伞从拉直瞬间直至投影直径最终达到稳定状态为止。考虑到降落伞拉直时的状态，故这里仅考虑伞衣径向的折叠，其充气过程的初始折叠状态可以简化为锥形，假人载荷直接简化为单点悬挂(如图3所示)。

所采用的ALE流固耦合数值方法不要求流体与结构进行一致性的网格划分，因此可以根据各自几何尺寸确定网格密度，之后直接将结构域与流体域耦合。伞衣用壳单元进行划分，伞绳用缆索单元进行划分，流体网格则采用六面体单元进行划分。显式积分时间步长取为6.00E-06 s，仿真过程的有限元模型信息如表2所示。

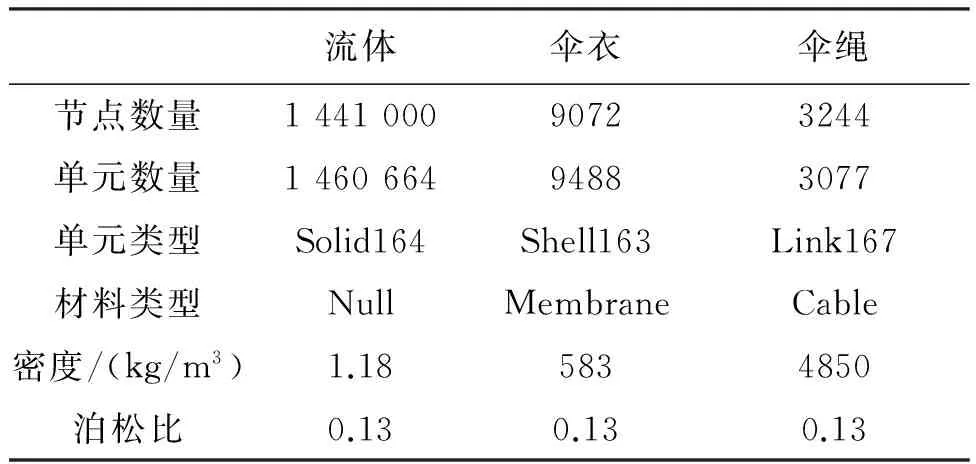
表2　流固耦合数值模型信息

5　计算结果分析

5.1伞衣外形分析

降落伞充气过程是典型的随机过程，尤其是有限质量情况下，许多随机参数都会对充气性能产生显著影响。本文未考虑阵风等随机环境因素对充气过程的影响，图4为降落伞充气过程三维外形变化，从图中可以看出，充气的初始阶段，伞缝较为细小狭长。气流进入伞衣首先在顶部堆积，伞衣呈“乌贼”状，之后再带动伞衣向外、向下扩张，并逐渐充满。相比无限质量情况而言，降落伞有限质量充气过程外形变化更剧烈，且更具有随机性。

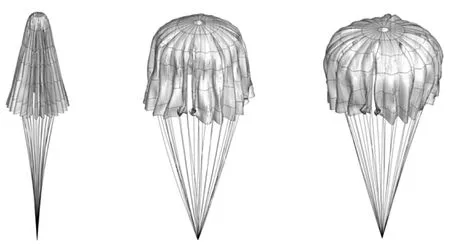
(a) t=0.05 s　　(b) t=0.1 s　　(c) t=0.3 s

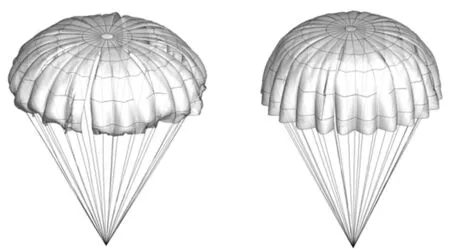
(d) t=1.2 s　　　　　　(e) t=2 s图4　降落伞开伞过程三维外形变化Fig.4　3D shape of canopy during inflation

图5为伞衣阻力面积变化对比曲线，可以看出，随着投放速度的增加，降落伞的充气时间缩短(这里的充气时间定义为阻力面积首次达到峰值的时间)，但投放速度对阻力面积影响不大，三个工况的最大充满面积和稳态阻力面积均无明显变化。

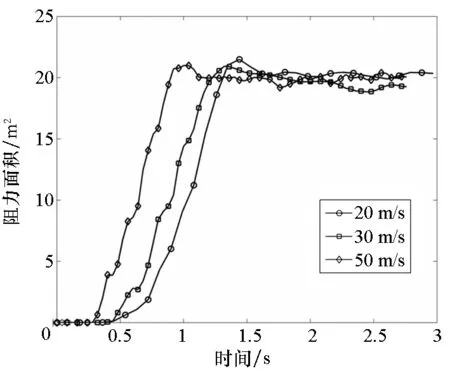
图5　伞衣阻力面积变化Fig.5　Results of canopy drag area

5.2流固耦合分析

图6为充气过程的伞衣周围流场速度和压力分布云图，从图中可以看出，在降落伞结构的作用下伞衣底部前缘附近的流场被加速，产生附加质量力并作用在伞衣外表面，当伞衣尾流的速度超过降落伞的速度时，通常会出现尾流再附现象，容易造成伞衣塌陷。伞衣肩部出现低速区(如图6(a)中流线所示)，形成绕流，结合顶孔气流的加速分离作用，从而形成顶端局部的负压区。

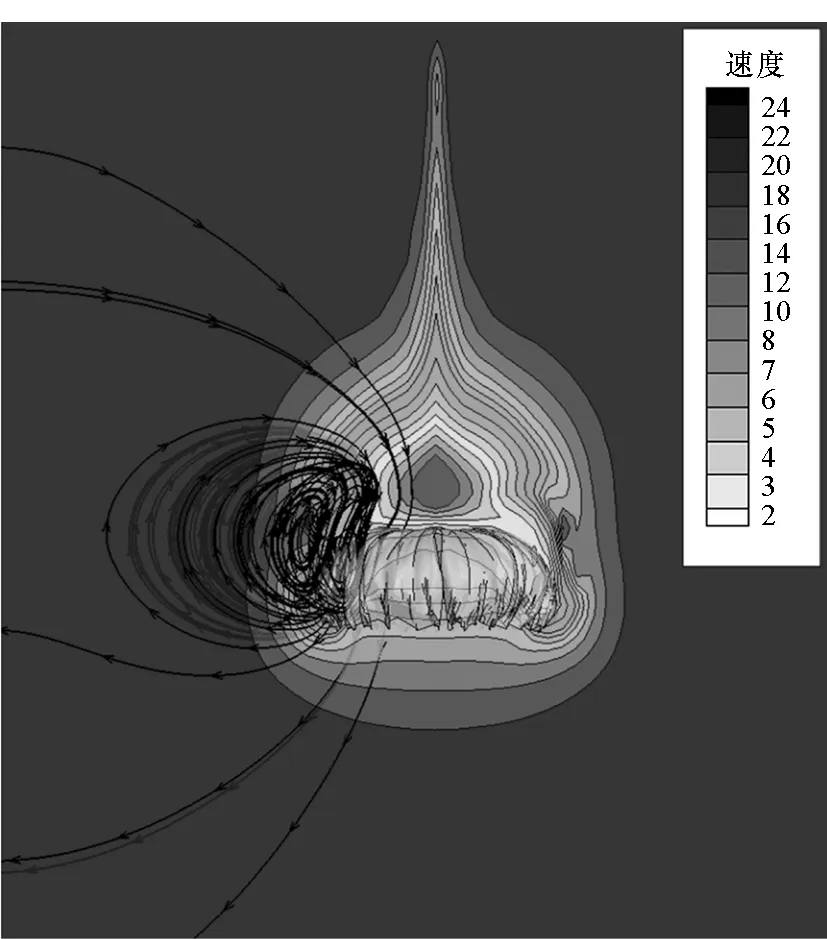
(a) 速度矢量云图(a) Velocity contour

(b) 压力矢量云图(b) Pressure contour图6　充气过程伞衣周围流场压力和速度分布云图Fig.6　Pressure distributions and velocity contours of canopy during inflation

5.3伞衣动载曲线

图7给出了充气过程挂重的开伞动载变化曲线，并结合空投试验数据进行了对比。挂重的质量为300 kg，从图中可以明显看出开伞力的变化趋势，开伞动载峰值达到23 g，仿真曲线与真实情况的变化趋势一致。相对于试验曲线结果，计算结果的开伞力峰值开始时间要提前0.1 s左右，这是因为本文所假定的初始折叠模型同实际伞衣拉直状态相比，张满程度更大，这样可以避免伞衣之间的初始接触，便于计算的收敛和充气过程的进行。有限质量充气环境下，伞弹系统无约束状态飞行，此时相对来流速度会减小，从而开伞力会出现明显的回落，相对于无限质量充气过程，有限质量开伞力的峰值也会明显降低[14]。同时可以看出开伞动载的峰值并未出现在伞衣充满瞬间，而是明显早于开伞时间。

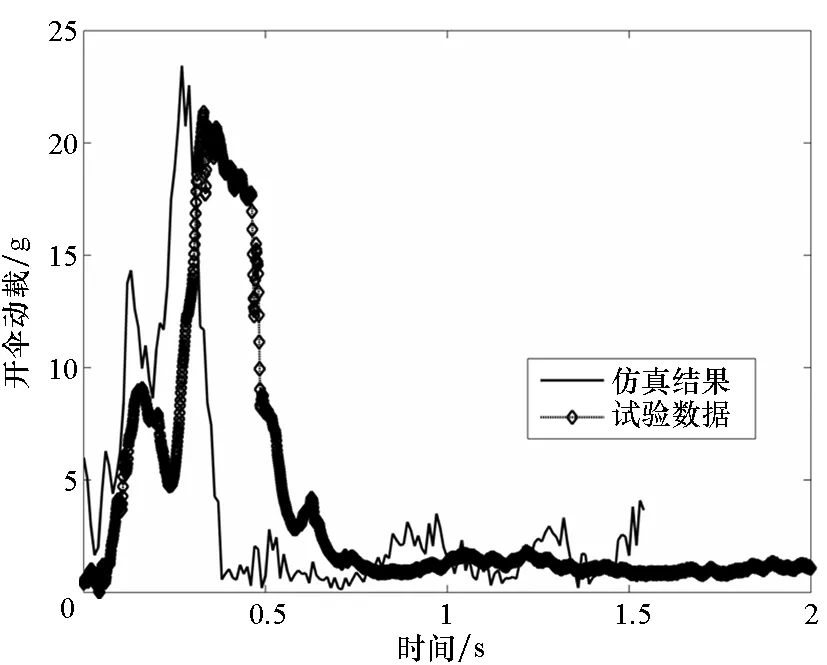
图7　开伞动载对比Fig.7　Comparison of opening load

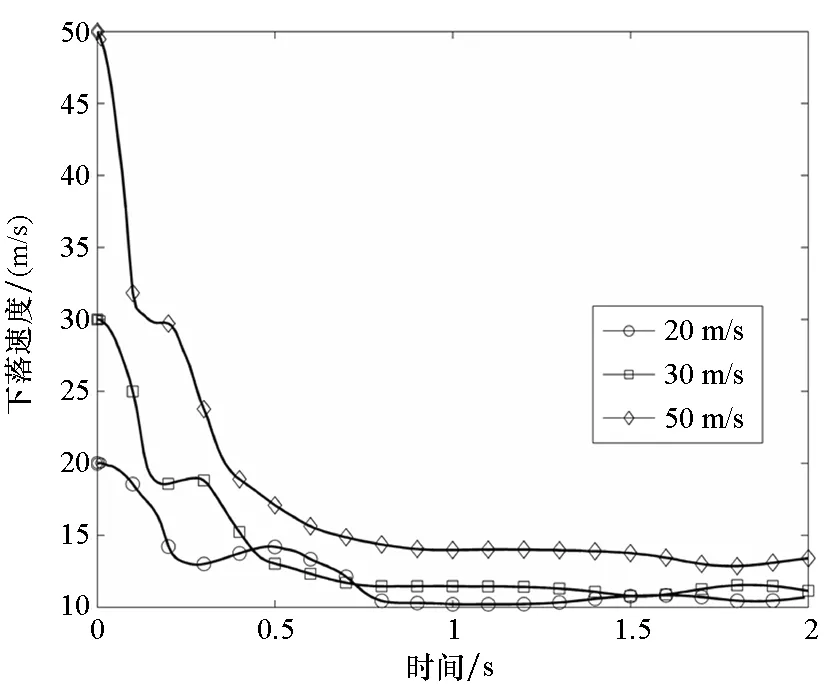
图8　下落速度变化对比Fig.8　Results of dropping velocity

5.4下落速度分析

对于有限质量充气过程，降落伞和挂重的下落速度不断减小。当阻力和重力达到平衡状态，下落速度达到恒定值，开始稳降阶段。图8给出了降落伞挂重下落过程的速度曲线变化，对比不同的初始空投速度可以看出，初始充气阶段的减速行为明显，充满之后基本保持稳定。同时可以看出，空投速度越大，充满时间越短。

6　结论

采用ALE流固耦合算法，数值模拟了低速空投过程降落伞有限质量充气过程的流固耦合动力学行为，采用动网格技术，减少了流场网格数量，提高了计算效率。对比试验数据进行分析，结果表明：在有限质量开伞条件下，伞衣周围的气流容易在降落伞结构的作用下被加速，产生附加质量力，在尾流区域产生再附现象，容易造成伞衣塌陷；随着投放速度的增加，伞衣充气时间缩短，且有限质量环境下开伞力峰值出现时间要早于开伞时间，之后伞衣沿径向逐渐充满，伞衣表面压力分布趋于均匀。

本文所采用的方法可以有效地预测降落伞空投过程动力学行为，结合多体系统的动力方程和稳定性分析理论，可以进一步对降落伞有限质量开伞过程的轨迹和随机扰动等动力学行为进行深入研究。

References)

[1]Ewing E G, Knacke T W, Wbixby H. Recovery systems design guide[M]. Beijing: Aviation Industry Press, 1978.

[2]Wolf D. A simplified dynamics model of parachute inflation[J].Journal of Aircraft, 1874, 11(1): 28-33.

[3]Potvin J, Peek G, Brocato B, et al. Inflation and glide studies of slider-reefed cruciform parachutes [C]//Proceedings of 16th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2001: AIAA 2001-2021.

[4]Takizawa K,Tezduyar T E. Computational methods for parachute fluid-structure interactions [J]. Archives of Computational Methods in Engineering, 2012, 19(1): 125-169.

[5]Sathe S, Benney A R, Charles R, et al. Fluid-structure interaction modeling of complex parachute designs with the space-time finite element techniques [J]. Computers & Fluids, 2007, 36 (1): 127-135.

[6]Kim J D, Li Y, Li X L.Simulation of parachute FSI using the front tracking method[J]. Journal of Fluids and Structures, 2013, 37: 100-119.

[7]Tutt B, Roland S, Charles R D, et al. Finite mass simulation techniques in LS-DYNA[C]//Proceedings of 21th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland, 2011: AIAA 2011-2592.

[8]彭勇， 张青斌， 秦子增. 降落伞主充气阶段数值模拟[J]. 国防科技大学学报, 2004, 26 (2): 13-16.

PENG Yong, ZHANG Qingbin, QIN Zizeng. Simulation of parachute final inflation phase[J]. Journal of National University of Defense Technology, 2004, 26(2): 13-16. (in Chinese)

[9]程涵, 余莉, 杨雪松, 等. 有限质量情况下降落伞开伞过程数值模拟研究 [J]. 空气动力学学报, 2014, 32 (2): 258-263.

CHENG Han, YU Li, YANG Xuesong,et al. Numerical simulation of parachute opening process in finite mass simulation [J]. Acta Aerodynamica Sinica, 2014, 32 (2): 258-263.(in Chinese)

[10]刘巍, 寇宝华, 葛建全, 等. 降落伞充满稳定阶段流场数值模拟 [J]. 中国空间科学技术, 2007, 27(1): 61-64.

LIU Wei, KOU Baohua, GE Jianquan,et al. Numerical simulation of flow field of the parachute fully developed[J]. Chinese Space Science and Technology, 2007, 27(1): 61-64. (in Chinese)

[11]Wang J, Aquelet N, Benjamin T, et al. Porous Euler-Lagrange coupling application to parachute dynamics[C]//Proceedings of 9th International LS-DYNA Users Conference, 2005.

[12]高兴龙， 唐乾刚， 张青斌， 等. 开缝伞充气过程流固耦合数值研究 [J]. 航空学报, 2013, 34 (10): 2265-2276.

GAO Xinglong, TANG Qiangang, ZHANG Qingbin, et al. Numerical study on fluid-structure interaction of slot parachute′s inflation process [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2265-2276. (in Chinese)

[13]Ben T, Taylor A P. The use of LS-DYNA to simulate the inflation of a parachute canopy [C]//Proceedings of 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2005: AIAA 2005-1608.

[14]Cockrell D J. The aerodynamics of parachutes[R]. North Atlantic Treaty Organization, 1987.

Numerical simulation on finite mass inflation dynamics of parachute

GAO Xinglong1，2, ZHANG Qingbin1, GAO Qingyu1, TANG Qiangang1, YANG Tao1

(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China；2. Facility Design and Instrumentation Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China)

In order to study the finite mass inflation dynamic behavior of parachute at an airdrop mission, the penalty coupling algorithm and the adaptive mesh technology were used to analyze the fluid-structure interaction characteristics between the flexible parachute structure and the surrounding incompressible flow field. The three dimensional dynamic opening profiles of parachute were numerically simulated and some parameters of parachute system like dropping velocities and drag coefficients were obtained; the influences of initial dropping velocity on filling time and drag area were compared; the trajectory was validated by the experimental data from airdrop tests. The computation results show that this method can efficiently simulate the dynamic characteristics of finite mass inflation in parachute system. The simulation results coincide with the test results.

parachute; fluid-structure interaction; finite mass inflation; ALE moving mesh

10.11887/j.cn.201604029http://journal.nudt.edu.cn

2015-11-16

国家自然科学基金资助项目(11272345，51375486)；国防科技大学校预研计划资助项目(JC13-01-04)

高兴龙(1987—)，男，吉林蛟河人，博士研究生，E-mail：18674853560@163.com； 张青斌(通信作者)，男，副教授，博士，硕士生导师，E-mail：qingbinzhang@sina.com

TP316

A

1001-2486(2016)04-185-06