两道同侧扫掠激波作用下形成的三维平板边界层*

何　刚，周　进

(国防科技大学 航天科学与工程学院， 湖南 长沙　410073)



两道同侧扫掠激波作用下形成的三维平板边界层*

何刚，周进

(国防科技大学 航天科学与工程学院， 湖南 长沙410073)

为探索一种减弱扫掠激波/边界层干扰强度的侧压方式，采用数值计算方法研究两道同侧扫掠激波作用下形成的三维平板边界层。对三维边界层的流动机理进行研究，并与相同气流偏转角的一道扫掠激波作用下形成的三维边界层进行定量比较。研究表明，存在两道同侧扫掠激波时，第一道扫掠激波使侧壁附近边界层变薄，进而使第二道扫掠激波与再附形成的边界层的相互作用减弱，从而总的效果是两道扫掠激波与边界层的相互作用强度比一道扫掠激波的弱；两道扫掠激波的气流总偏转角与一道扫掠激波的相同，相交后汇聚成的激波强度与一道扫掠激波的基本相同，之前被两道扫掠激波“扫”起来的边界层在汇聚激波作用下还呈现锥形流动，分离线和来流的夹角也与一道扫掠激波的基本相同。

扫掠激波/边界层干扰；三维边界层；高超声速进气道；边界层分离

高超声速进气道中广泛存在着激波与边界层的相互干扰，其一直是进气道设计所关心的问题。侧压式进气道中，扫掠激波与边界层的相互作用不仅影响着起动性能[1-3]，而且使流动更加复杂。由于前体有多个楔角产生多道斜激波，进气道的侧板边界层就会受多道同侧扫掠激波的作用而产生分离[4]。为改进侧压式进气道、提高效率，通常将侧板改成曲面以降低激波/边界层相互干扰强度[5-7]，但这样就增加了复杂性。由多个压缩平面构成的侧板或许是减弱激波/边界层干扰的有效方法，但这也带来了多道同侧扫掠激波与边界层相互干扰的基本问题。

目前，扫掠激波/边界层干扰问题的研究主要集中在两类问题上：一是由一个侧壁产生的扫掠激波与边界层的相互作用[8-9]；一是由双侧壁产生的两道交叉激波与边界层的相互作用[10-12]。对于后者，可以看作是一道扫掠激波与边界层的相互作用受到了异侧的另一道扫掠激波的干扰。而一道扫掠激波与边界层的相互作用，受到同侧另一道扫掠激波的干扰，即两道同侧扫掠激波与边界层的相互作用是对这一问题的延伸。目前这一问题还未见文献研究报道。

本文拟采用数值模拟方法研究两道同侧扫掠激波与边界层相互干扰的问题。将典型参数条件下与相同气流偏转角条件下的一道扫掠激波与边界层相互干扰的流场进行定性和定量对比分析，以研究流动的机理，并探索一种减弱扫掠激波与边界层相互干扰强度的侧压方式。

1　研究条件和计算方法

1.1研究条件

图1为研究两道同侧扫掠激波与平板边界层相互干扰的几何模型(单位：mm)。来流马赫数为3，总压P0为1个大气压，总温T0为300 K，湍流度为1%。侧板有两个侧压角(气流偏转角)，分别产生一道扫掠激波。当α2=0°时问题退化为一道扫掠激波与边界层相互干扰的问题。在图1所示流动条件下，侧板前缘处来流边界层的厚度δ0.99= 3.4 mm。

图1　计算的几何条件Fig.1　Configuration for calculation

根据同侧激波相交的理论，只要气流最终偏转角一致，经过两道斜激波作用下的气流的压升系数σP和一道斜激波作用下的差别不大，近似计算时可忽略[13]。对于本文来流马赫数为3的情况，在α1+α2=20°时，随着α1变化，σP最大偏差为1.7%。为与一道扫掠激波的情况(α1=20°)作对比，本文设定α1+α2=20°并分别计算了α1为 5°，10°，15°，20°时的4个算例。

两道扫掠激波相交后合成一道更强的扫掠激波。根据斜激波相交的理论，波后的σP基本相当于一道相同气流偏转角的激波作用后的[13]。

1.2计算方法

数值计算采用的控制方程为理想气体可压N-S方程，采用三维定常隐式求解器求解。来流气体为空气，比热比为1.4。气体分子黏性采用Sutherland公式计算，湍流模型采用k-ωSST模型[1, 12]。方程的离散采用有限体积法，无黏项采用二阶Roe格式离散，黏性项采用二阶中心差分格式离散。文献[14]对侧压角为12°的扫掠激波/边界层干扰进行了数值仿真并与实验作了对比。文献中采用的数值方法和来流条件与本文的相同，仿真结果与实验结果获得的流场吻合较好，表明仿真计算具有较高的可靠性。这也表明了本文采用的数值仿真方法可以较好地模拟扫掠激波/边界层相互作用的流场。

计算域如图1所示。壁面的边界条件设置为绝热无滑移壁面，流场的入口设置为压力远场，出口设置为压力出口。由于法向和展向空间足够大，其余的边界设置为对称面。流场区域的划分采用结构网格，并向壁面加密。壁面第一层网格的高度为0.05 mm，以保证壁面附近流动y+≈1。本文的4个算例流场相似，计算的网格量一样，所以用α1=20°的算例为代表做网格无关性验证。对三套网格做了计算，网格量分别为：180×60×60，240×80×80，300×100×100。下平板上的分离线拟合的直线与来流的夹角分别为49.4°，49.9°，49.9°，x=300 mm平面内边界层的厚度H(H为下平板边界层中总压恢复系数等于0.8的轮廓与下平板的最大距离)分别为7.18 mm，7.04 mm，6.95 mm。可见，采用第三套网格计算得到的流场和第二套网格的相比变化很小，网格对计算结果的影响可忽略。本文计算采用的是第三套网格。

2　结果和分析

2.1流动机理分析

选取α1=10°，α2=10°算例的流场代表两道扫掠激波与边界层相互作用的流场，与α1=20°，α2=0°算例的流场，即一道扫掠激波与边界层相互作用的流场进行对比分析。

从图2的云图可见(文中标值的单位为mm，压力的单位为Pa)，图2(b)的主流经过两道扫掠激波的压缩后总压恢复系数σP0比图2(a)经过一道扫掠激波的大。底板附近的σP0定性地显示了边界层的分布。可见，在两个算例中，边界层都在激波的作用下沿展向远离侧壁的方向运动并堆积形成锥形流动，从而侧壁附近的底板上边界层变得很薄。从底板附近的σP0分布来看，图2(a)中的最后一个流向截面的低σP0区域明显比图2(b)的大，表明图2(a)的激波边界层相互作用比图2(b)的强。

从图2的压力等值线来看，图2(a)中的扫掠激波与图2(b)中的第一道扫掠激波在与边界层相互作用后都呈现“λ”结构。而图2(b)的第二道扫掠激波的“λ”结构不明显，并且激波在法向上延伸到离底板更近的位置。这表明第二道激波与边界层的相互作用较弱。从图2(b)最后一个截面可见，两道扫掠激波相交后在主流中合成一道激波，在边界层里合成一个“λ”结构。这表明经过两道扫掠激波作用后，边界层在汇聚激波作用下还呈现一道扫掠激波作用下形成的锥形流动结构。

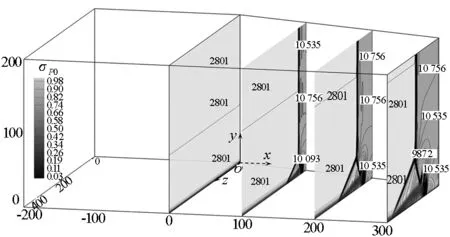
(a) α1=20°, α2=0°

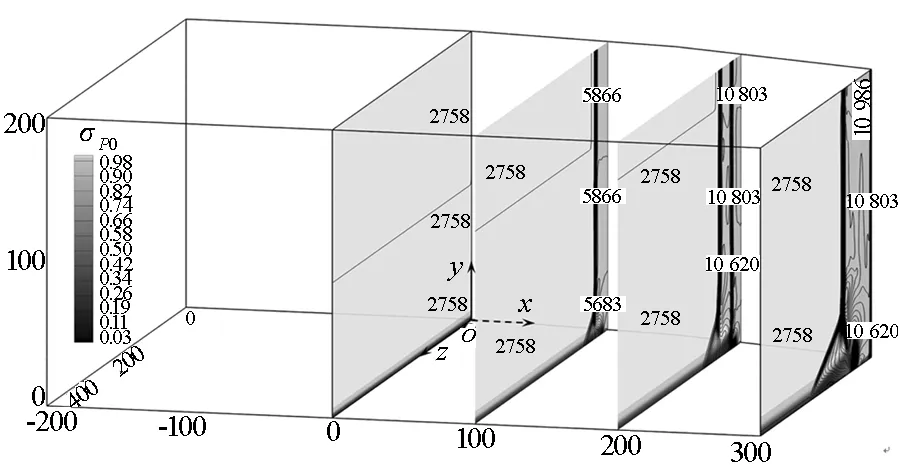
(b) α1=10°, α2=10°图2　流向横截面σP0和压力的分布Fig.2　Distribution of σP0 and pressure in transverse slice

图3给出了两个算例底壁上摩擦力线(以底壁的摩擦应力为矢量作流线)以及压力(云图、等值线)的分布。

从图3(a)可见，整个底壁被摩擦力线组成的两条线分为三个区域：一条是分离线S1，一条是再附线R1。两条线近乎直线，它们之间的区域压力变化较小。S1上游受侧压影响较小，摩擦力线近乎直线(实际上此区域还包含一条上游影响线，此处不讨论)。R1下游压力较高，这是因为激波波后压力更高。而再附线附近压力比壁面附近压力高是因为主流的流体跨过堆积起来的边界层向壁面运动时因转向平行壁面流动受到了进一步压缩。

从图3(b)可见，在第一道扫掠激波作用下，底壁上的压力和摩擦力线分布与图3(a)相似，但在第二道扫掠激波作用下分离线S1转了一个角度(用S0来表示)。在两道扫掠激波共同作用下，分离线和再附线还是近乎直线，分离区内压力变化不大，分离区还是呈现锥形流动的特征。

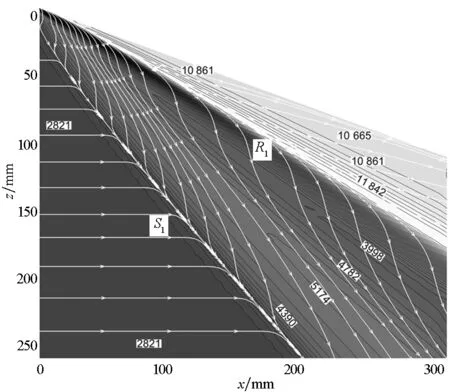
(a) α1=20°, α2=0°

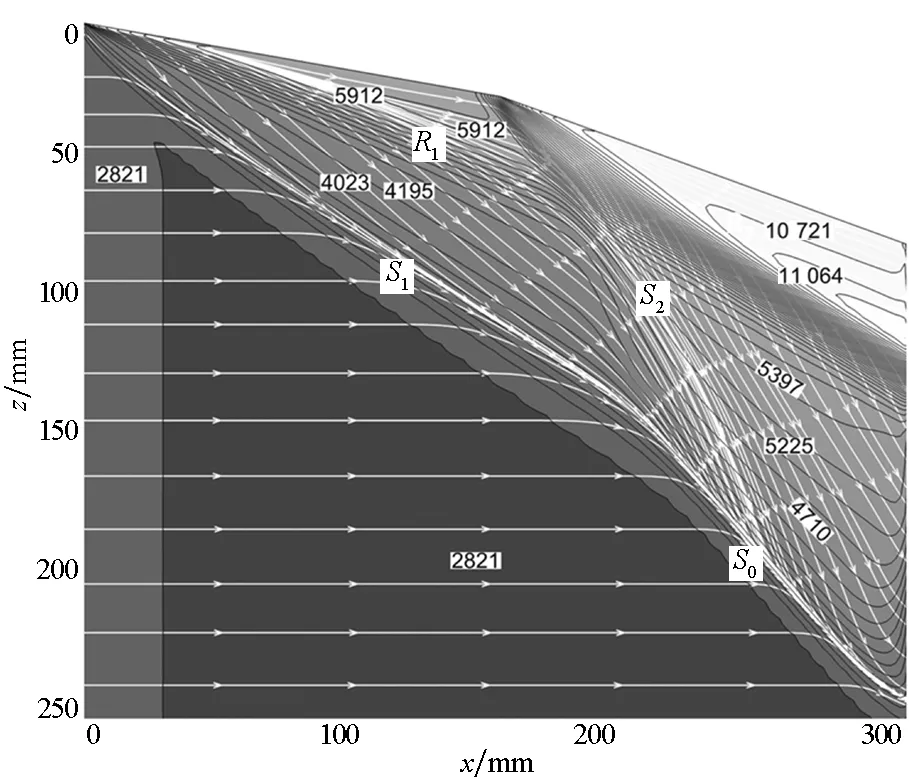
(b) α1=10°, α2=10°图3　底壁摩擦力线与压力的分布Fig.3　Distribution of shear stress lines and pressure

2.2两道扫掠激波与一道扫掠激波对边界层作用的定量比较

对于两道扫掠激波与边界层相互作用的算例，第一道扫掠激波使边界层被“扫”离侧壁，第二道扫掠激波由于壁面附近边界层变薄而作用减弱，使得两道扫掠激波与边界层的相互作用相比一道扫掠激波的弱。下面定量地比较两种侧压方式形成的三维边界层。

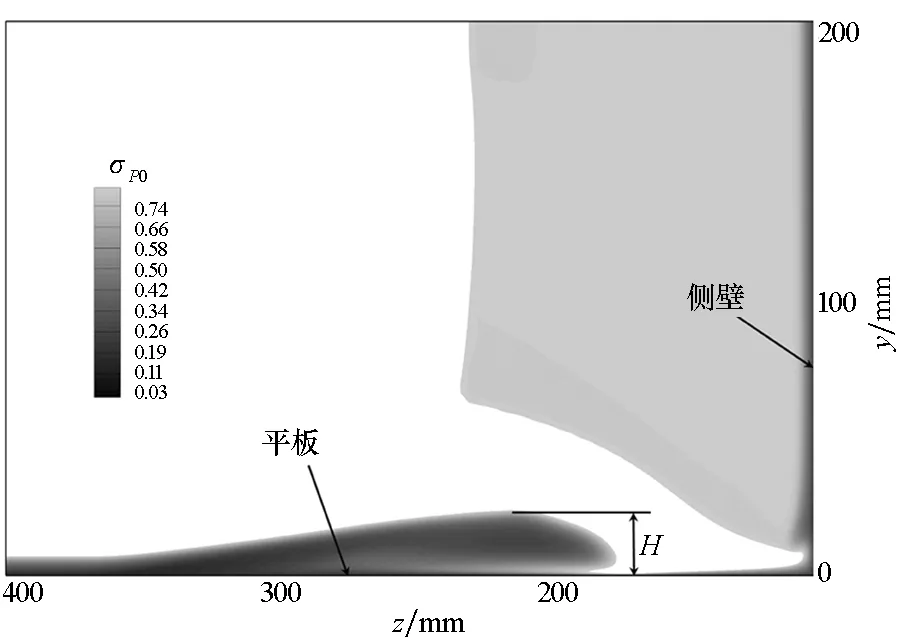
(a) α1=20°, α2=0°

(b) α1=10°, α2=10°图4　x=300 mm流向横截面内σP0的分布(逆流向观察)Fig.4　Distribution of σP0 in transverse slice when x=300 mm(looking upstream)

为了定量地比较激波边界层干扰强度，定义边界层厚度参数H，用以表示边界层中σP0=80%的外轮廓的高度，如图4所示。图4中只显示了x=300 mm流向截面内σP0≤80%的云图。从图4可以定性地看出一道扫掠激波作用下边界层的厚度更大，边界层内的低能流体所占的面积更多，说明扫掠激波与边界层相互干扰的强度更大。表1定量地给出了H随α1变化的情况。

表1　H随α1变化的情况

从表1可见，随着α1的增大，H越大，但都小于一道扫掠激波(α1=20°)作用后的。这表明将一道扫掠激波分成两道可以减弱激波边界层干扰强度。但同时也注意到，由于第一道激波作用的距离比第二道激波大，所以第一道激波α1越大激波强度越大，从而总的效果是α1越大H越厚。

表2给出了两道激波相交后分离线S0与来流夹角αS0随α1的变化情况，同时也给出了相同气流偏转角下侧壁是Prandtl-Mayer压缩时，压缩波汇聚成扫掠激波后与边界层相互作用形成的分离线的角度。

表2　分离线偏转角随α1的变化情况

从表2可见，虽然各算例侧压历程不同，但激波/压缩波汇聚成一道扫掠激波后边界层分离线的角度相差不大(最大偏差为6.8%)。由于来流条件相同，侧压后主流的气流偏转角相同，最后汇聚成的扫掠激波强度也基本相同。由此可以推断，在来流条件(马赫数、边界层厚度)不变的情况下，最终的离线角度只与最后汇聚成的激波的强度有关，与激波汇聚前的侧压过程无关。

3　结论

通过研究，得到以下结论：

1)两道同侧扫掠激波与边界层相互作用时，第一道扫掠激波使壁面附近边界层变薄，使得第二道激波与再附形成的边界层的相互作用减弱，从而总的效果是在相同气流总偏转角条件下，两道扫掠激波与边界层的相互作用相对于一道扫掠激波的强度更弱。

2)两道同侧扫掠激波相交后汇聚成一道更强的扫掠激波。在这道汇聚的扫掠激波作用下，之前被两道扫掠激波“扫”起来的边界层还呈锥形流动。虽然侧压历程不同，但在汇聚激波作用下分离线与来流的夹角基本相同。因此可以推测在来流条件(马赫数、边界层厚度)不变的情况下，最终的分离线角度只与最后汇聚成的激波强度有关，与激波汇聚前的侧压过程无关。但这需要更多的计算和实验加以研究证明。

References)

[1]赵一龙, 范晓樯, 王翼, 等. 抽吸对高超侧压进气道自起动性能的影响 [J]. 航空动力学报, 2013, 28(5): 1101-1106.

ZHAO Yilong, FAN Xiaoqiang, WANG Yi, et al. Effects on bleeding on self-starting characteristics of side-compression hypersonic inlet [J]. Journal of Aerospace Power, 2013, 28(5): 1101-1106. (in Chinese)

[2]王翼, 范晓樯, 梁剑寒, 等. 三维侧压高超声速进气道不启动流场试验与数值模拟研究 [J]. 宇航学报, 2008, 29(6): 1927-1931.

WANG Yi, FAN Xiaoqiang, LIANG Jianhan, et al. Experimental and numerical investigation on the unstart flowfield of a three-dimensional sidewall compression hypersonic inlet[J]. Journal of Astronautics, 2008, 29(6): 1927-1931. (in Chinese)

[3]赵一龙, 范晓樯, 梁剑寒, 等. 侧板构型对高超侧压进气道起动性能的影响 [J]. 推进技术, 2014, 35(2): 145-150.

ZHAO Yilong, FAN Xiaoqiang, LIANG Jianhan, et al. Impacts of sidewall geometry on starting characteristics of side-compression hypersonic inlet [J]. Journal of Propulsion Technology, 2014, 35(2): 145-150. (in Chinese)

[4]肖雅彬, 岳连捷, 龚鹏, 等. 三面压缩式高超声速进气道流动结构研究[J]. 实验流体力学, 2008, 22(2): 64-67.

XIAO Yabin， YUE Lianjie， GONG Peng, et al. Research on the flow pattern of three dimensional compression hypersonic inlet [J]. Journal of Experiments in Fluid Mechanics, 2008, 22(2): 64-67. (in Chinese)

[5]Korte J J, Singht D J, Kumart A, et al. Numerical study of the performance of swept, curved compression surface scramjet inlets [J]. Journal of Propulsion and Power, 1993, 10(6): 841-847.

[6]Zhang L, Zhang K Y, Wang L. Experimental study of three-dimensional sidewall inlet designed on wall Mach number linear distribution curved surface[C]//Proceedings of 20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2015: AIAA 2015-3669.

[7]何刚, 赵玉新, 周进. 等熵侧压诱导的超声速平板边界层二次流研究 [J]. 推进技术， 2016， 37(9): 1624-1630.

HE Gang, ZHAO Yuxin, ZHOU Jin. Investigation on secondary-flows of a supersonic flat-plate boundary layer induced by isentropic sidewall compression [J]. Journal of Propulsion Technology, 2016, 37(9): 1624-1630. (in Chinese)

[8]Alvi F S, Settles G S. A physical model of the swept shock wave/boundary-layer interaction flowfield [C]//Proceedings of 22nd Fluid Dynamics, Plasma Dynamics and Lasers Conference, 1991: AIAA 91-1768.

[9]Martis R R, Misra A, Singh A, et al. Effect of micro-ramps on separated swept shock wave-boundary-layer interactions[J]. AIAA Journal, 2014, 52(3): 591-603.

[10]Knight D, Gnedin M, Becht R, et al. Numerical simulation of crossing shock wave/turbulent boundary layer interaction using a two-equation model of turbulence [J]. Journal of Fluid Mechanics, 2000, 409(1): 121-149.

[11]Croker B A. Numerical investigations of 3-D swept shock interaction control with porous surfaces [C]//Proceedings of 3rd AIAA Flow Control Conference, 2006: AIAA 2006-3346.

[12]金亮, 梁剑寒, 孙明波, 等. 交叉激波湍流边界层干扰问题数值模拟 [J]. 国防科技大学学报, 2008, 30(3): 11-14.JIN Liang， LIANG Jianhan， SUN Mingbo, et al. CFD analysis for crossing shock wave/turbulent boundary layer interactions[J]. Journal of National University of Defense Technology, 2008, 30(3): 11-14. (in Chinese)

[13]童秉纲， 孔祥言， 邓国华. 气体动力学 [M].2版. 北京：高等教育出版社, 2012.

TONG Binggang, KONG Xiangyan, DENG Guohua. Gas dynamics[M]. 2nd ed.Beijing: Higher Education Press, 2012.(in Chinese)

[14]赵一龙. 高超声速进气道分离流动建模及不起动机理研究 [D]. 长沙：国防科学技术大学, 2014.

ZHAO Yilong. The study of separated flow modeling and unstart mechanism of hypersonic inlet [D]. Changsha: National University of Defense Technology, 2014. (in Chinese)

Three-dimensional flat-plate boundary layers generated by two swept shock waves of the same side

HE Gang, ZHOU Jin

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

In order to seek a sidewall compression method to weaken the interaction between swept shock waves of the same side and boundary layers, the three-dimensional flat-plate boundary layer generated by the interaction of two swept shock waves of the same side and the flat-plate boundary layer was numerically studied. The flow mechanism of this three-dimensional boundary layer was analyzed. Also, the three-dimensional boundary layer was quantitatively compared with the one generated by one swept shock wave which has the same flow deflection angle. The results show that, in the case of two swept shock waves, the first swept shock wave makes the boundary layer next to the sidewall thinner, so the interaction between the second shock wave and the boundary layer in the attachment region becomes weaker, leading to the total effect that the interaction between two shock waves and the boundary layer is weaker than that at the one swept shock wave case; the total flow deflection angle of two swept shock waves is the same as one shock wave case, so the strength of the converged shock wave is essentially the same; the three-dimensional boundary layer generated by the swept shock is still conical, and the angle between the separation line and the inflow is essentially the same with the one swept shock case.

swept shock wave/boundary layer interaction; three-dimensional boundary layer; hypersonic inlet; boundary layer separation

10.11887/j.cn.201604006http://journal.nudt.edu.cn

2015-10-18

国家自然科学基金资助项目(11472304)

何刚(1987—)，男，四川南充人，博士研究生，E-mail：hegang87@nudt.edu.cn；周进(通信作者)，男，教授，博士，博士生导师，E-mail：zj706@vip.sina.com

TN95

A

1001-2486(2016)04-034-05