基于单元变形的网格间流场信息传递方法*
董海波,徐春光,刘 君
(大连理工大学 航空航天学院, 辽宁 大连 116024)
基于单元变形的网格间流场信息传递方法*
董海波,徐春光,刘君
(大连理工大学 航空航天学院, 辽宁 大连116024)
针对单元网格发生变形重构中新旧网格之间的数据插值问题,提出一种基于格点格式有限体积法的流场数据传递方法。利用非结构动网格技术,将旧网格单元移动到新网格单元,同时时间推进求解流场控制方程,获得移动后旧网格单元物理量,并将其赋给新网格单元,以此来实现两套网格间的信息传递。计算结果表明,该方法在信息传递过程中没有引入插值误差,理论上流场求解方法的精度就是信息传递精度,验证结果表明其显著优于二阶插值精度。
数据插值;径向基函数;动网格;网格重构
在包含运动边界的非定常流动模拟中,流场物理空间随时间变化,边界运动导致网格也随时间变化,典型应用包括多体分离,机翼抖振、颤振、舱门启闭等[1-2]。计算流体力学(Computational Fluid Dynamics, CFD)计算一般采用运动嵌套网格、笛卡尔自适应网格和变形动网格等技术处理网格变化。在采用上述技术处理网格变化时,均涉及流场信息的插值问题[3-4],即利用旧网格上的流场信息插值获得重构区域流动参数。
网格间流场信息插值可分为非守恒型插值和守恒型插值两类。非守恒型插值方法有逆距离加权插值、线性插值[5]等方法,插值过程中该类方法不满足守恒特性,会降低计算精度且无法捕捉激波的正确位置[6]。守恒型插值方法,主要有基于面通量(Simplified Face-Based Donor-Cell, SFB/DC)的方法和基于单元相交(Cell-Intersection-Based Donor-Cell, CIB/DC)的方法[7]。其中,CIB/DC方法思想简单直接,对计算网格的类型、结构不进行任何假设,适用范围很广,并且具有保号性,插值过程中不会产生新的极值[7]。文献[8-10]给出了利用本质无振荡(Essentially Non-Oscillatory, ENO)重构单元物理量分布的CIB/DC守恒插值方法,实现了二维网格条件下的守恒插值。文献[11]发展了一种适用于二维/三维混合网格的CIB/DC精确守恒插值方法,实现了插值过程中守恒量的严格守恒。
上述方法的插值过程是在同一时间层完成,即利用n时刻旧网格流场信息,通过数学方法插值获得同一时刻新网格的流场信息,插值过程不涉及时间变量,只体现了新旧网格在空间上的关联性。文献[12]从波动方程出发,证明了“计算流场过程中的插值运算,会引起差分格式的相容性变化,从而导致解的精度降低”,并且插值后的流场参数会出现非物理振荡[13]。
为解决上述问题,发展了一种适用于格点格式的新型网格间信息传递方法。采用网格变形技术,随着时间推进求解控制方程,完成旧网格信息到新网格信息的传递。该算法与常用插值方法的原理完全不同,不引入新的插值误差,理论上流场求解算法的精度就是信息传递的精度。
1 基本思路
以二维网格为例说明网格变形信息传递新方法的技术原理。如图1所示,n时刻网格重构后的新网格点P落入旧网格单元ΔABC中。在n时刻旧网格基础上控制方程时间方向推进Δt,获得n+1时刻流场信息,同时利用动网格技术[14]将C点视为主动点移动至P位置。由于n+1时刻旧网格点C与新网格点P在空间位置重合,可把C点的流场信息直接赋值给P点。对重构区所有待插值点重复此操作,则新网格获得了n+1时刻完整的流场信息,实现了新旧网格间流场信息的传递。在C点移动过程中,为防止出现网格交错、穿越的情况,需要利用网格变形方法计算C点周围被动点A,B移动后的坐标。
与传统插值方法在同一时间层单纯利用新旧网格间的空间位置关系插值不同,本文方法通过求解流体控制方程结合动网格技术,获得新网格点物理量,克服了插值引入额外误差[12]的问题。
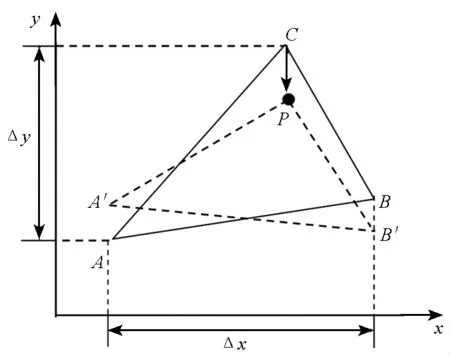
图1 二维网格变形信息传递方法Fig.1 Two-dimensional grid deformation information transfer method
2 二维问题网格变形信息传递方法
2.1网格变形信息传递方法
根据网格变形信息传递基本思路,以图1为例,给出二维条件下信息传递的详细步骤:
1)查找“贡献单元”,假设n时刻网格需要重构,P为重构后新网格格点,落入旧网格单元ΔABC中,可采用文献[14]介绍的查找方法;

3)根据稳定性条件,确定旧网格格点C移动至新网格格点P的时间步长,并计算获得整个插值区域的最小时间步长Δtmin;
4)根据时间步长Δtmin,以n时刻流场信息为初值,在旧网格上求解流体控制方程,得到n+1时刻的流场信息,同时将旧网格格点C视为主动点,利用非结构动网格技术[14]将其移动至新网格格点P,并采用文献[15]中的网格变形方法获得C点周围被动点A,B移动后的坐标;
5)将n+1时刻旧网格格点C的物理量直接赋给新网格格点P,得到新网格在n+1时刻流场信息,作为新旧网格信息传递后的起始流场,在新网格上开始下一步计算,新旧网格间的信息传递完成。
在上述步骤中,步骤1、步骤2、步骤5均为常用方法。步骤3中的Δtmin需要根据稳定性条件给出,下一节通过稳定性分析给出了二维条件下Δtmin的计算方法。步骤4中变形区域范围由流场求解精度确定。在时间推进一步条件下,对于非结构有限体积方法,二阶精度求解要用到求解单元周围两层网格单元的物理量[14],通常变形区域应包含周围两层单元。
2.2时间步长确定方法

信息传递过程中,假设在Δt时间内,C点移动到P点,则有:
(1)
其中:xv,yv为网格速度。根据流体计算稳定性条件[12],则有:
(2)
其中:V为单元面积;Δx,Δy为单元在x轴和y轴上的投影长度;a是当地声速;CFL为库朗数。
将式(2)限制进一步严格化,则有:
(3)
根据式(1)和式(3),可以得到:
(4)
式(4)有物理意义的条件是右端项大于0,即:
(5)
令
(6)
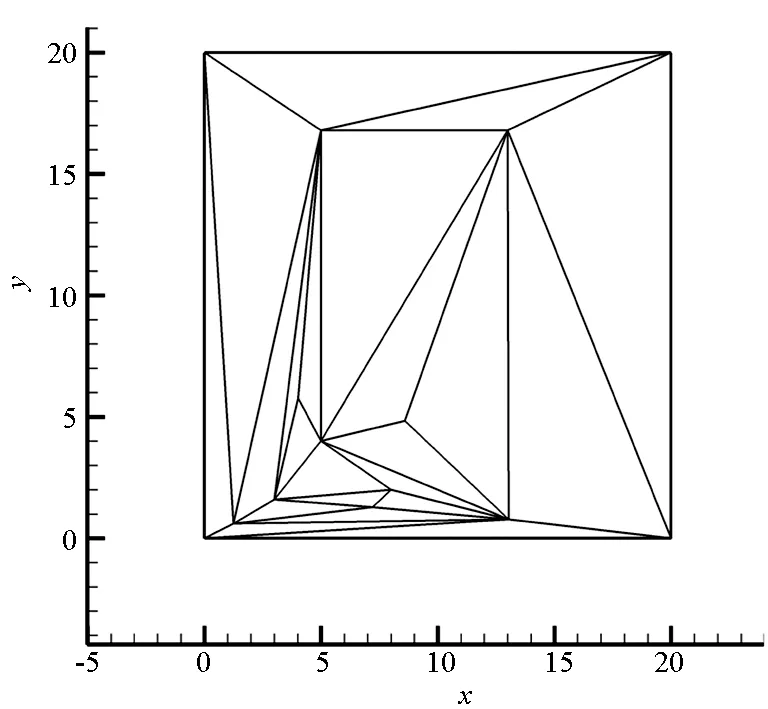
[12]中,将NV定义为移动网格库朗数。从式(6)可以看出,NV仅与C点和P点的相对位置有关,而与点的绝对坐标无关。为便于计算NV,可将当地坐标进行旋转平移,使C为坐标原点,P点落于y轴正向,则有:
(7)
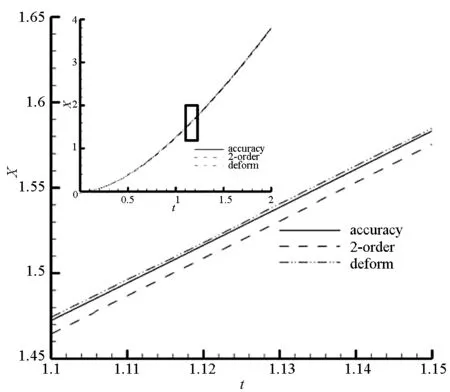
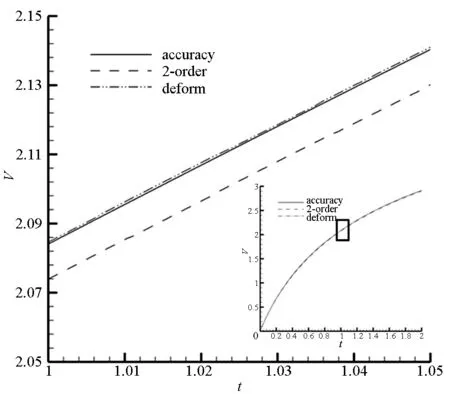
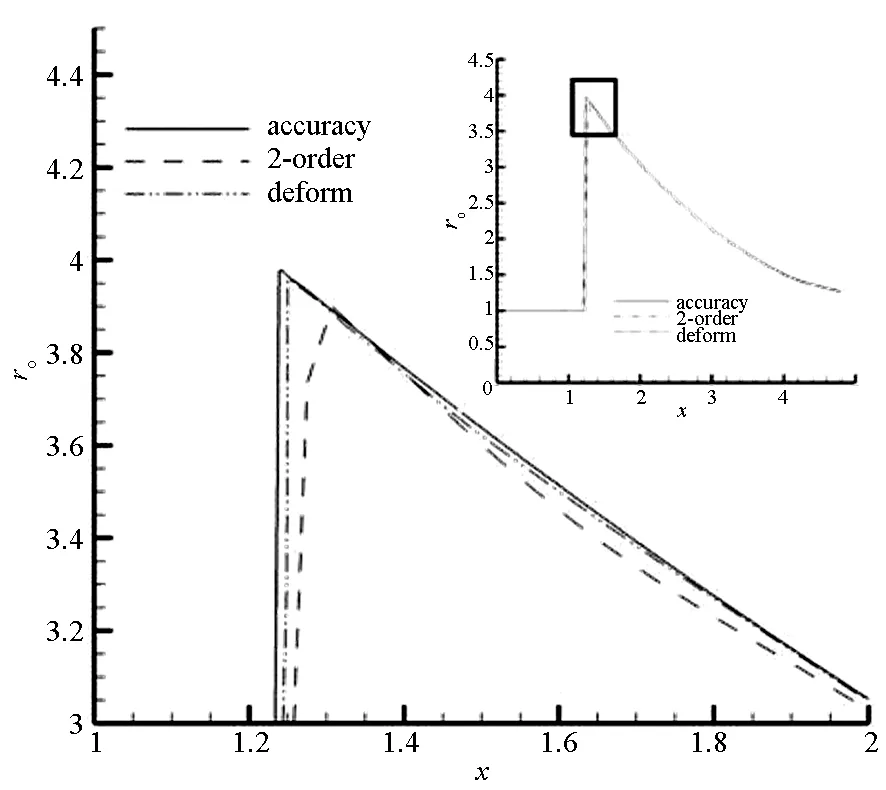
由式(5)可知,当NV N=[NV/CFL]+1 (8) 其中“[x]”表示不大于x的最大整数。 对重构区域内所有信息传递点,根据式(7)、式(8)计算各自的移动步数Ni,并取最大移动步数NMAX=max(Ni),文献[14]证明对于二维网格,最大移动步数NMAX不大于2,式(4)可表示为: (9) Vi表示新单元贡献单元i的面积,NV为网格移动库朗数。根据传值同步性原则取Δt=min(Δti)为新网格传值的单步计算时间。至此,给出了2.1节步骤3中需要确定的最小时间步长Δtmin。 2.3壁面附近单元信息传递方法 网格变形信息传递方法不需要将主动点周围各点进行刚性同步平移,从而不要求物体壁面上的节点必须跟随主动点平移,解决了壁面附近单元的信息传递问题。下面以二维情况为例,对壁面附近单元的信息传递方法进行说明。 图2中旧网格单元ΔABC的顶点B位于物体壁面,待插值点P落于ΔABC中。在网格变形信息传递过程中,主动点C移动至P点,并采用网格变形方法计算得到顶点A的新位置A′,位于物体壁面上的顶点B则保持不动,并同步求解流场控制方程,从而实现了物体壁面附近单元的信息传递。 图2 二维情况下壁面附近单元变形信息传递方法Fig.2 Two-dimensional grid near the wall deformation information transfer method 网格变形信息传递方法的思路是通过网格变形将旧网格点移动至新网格点,实现物理量的直接传递,采用变形能力强、效率高的网格变形算法是实现高精度信息传递的基础。 本文采用文献[15]提出的径向基函数方法(Radial Basis Function, RBF)与运动子网格方法(Moving Submesh Approach, MSA)混合的动网格变形算法处理信息传递过程中的网格变形问题。如图3所示的背景网格中,一个内点与旧网格中需要插值的待移动点重合,如图4中P点。如图5所示,主动点P移动至A点,其他内点移动后的坐标根据式(10)计算[16],变形后计算网格如图6所示。 (10) 其中:ei=Si/S(i=1,2,3);xi,yi分别为待求点所在背景网格三个顶点移动后的坐标;S为初始背景网格三角形单元的面积;Si为变形前待求坐标网格点与背景三角形单元3个顶点构成的小三角形面积,采用文献[16]中方法计算。 图3 初始背景网格Fig.3 Initial background grid 图4 背景网格与计算网格Fig.4 Initial background grid and computation grid 图5 初始背景网格与变形后背景网格Fig.5 Initial background grid and background grid after deformation 图6 变形后的计算网格Fig.6 Computation grid after deformation 4.1一维活塞运动 计算模型如图7所示,活塞初始位置位于x=1.0(无量纲)处,质量为5(无量纲),速度为0,在x=0.9(无量纲)处存在一个向左运动的激波,激波与活塞之间为高压静止气体,激波左侧为速度u=4.0(无量纲)的低压气体,活塞右侧为真空。活塞在压差的作用下向右运动,产生膨胀波向左传播,逐渐追上激波,使得波后压力逐渐下降。该算例与单纯的高压推动活塞运动算例相比,包含了激波、膨胀波及其相互作用,流场结构较为复杂,能够验证插值方法对激波捕捉、流场压力和密度以及物体运动参数的影响。 计算的初始无量纲参数如下: 1)激波左侧低压区:密度ρ0=1,速度u0=4,压力P0=1/γ; 2)激波右侧低压区:密度ρ0=5,速度u0=0,压力P0=29/γ; 3)活塞右侧为真空。 其中无量纲化的参考量为:γ=1.4;参考长度L∞=1 m;参考密度ρ∞=1 kg/m3;参考速度V∞=1000 m/s;参考压力P∞=1 000 000 Pa,参考时间t∞=1E-3 s;参考质量m∞=1 kg。 计算区域的初始无量纲长度L=1,在t=2 (无量纲)计算结束。 图7 一维活塞计算模型Fig.7 A one-dimensional model for calculating the piston 流场计算采用一维模型,建立两套网格,第一套网格单元数为200,第二套网格单元数为150,在活塞运动过程中进行往复插值,即在第一套网格情况下计算20步,将流场数据插值到第二套网格继续进行计算,计算20步之后再将流场数据插值到第一套网格继续进行计算,共计算约3500步,往复插值175次。 计算过程中分别采用二阶插值和网格变形插值方法进行往复插值。此外,为了建立比较的基准,建立了一套单元数为1000的网格进行计算,并且计算过程中不进行插值,作为近似精确解使用。 图8和图9分别为活塞运动位置和速度的变化情况,由于误差相对于精确值是个小量,在全局图中很难看出不同插值方法的差异。因此,图中显示的主图为全局图中方框标注位置的局部放大,可以看出利用本文网格变形插值方法得到的计算结果与密网格、无插值得到的计算结果非常接近,计算精度明显优于二阶插值方法的计算结果。 图8 活塞位置随时间变化规律Fig.8 Relationship between piston position and time 图9 活塞速度随时间变化规律Fig.9 Relationship between piston velocity and time 活塞向右侧运动过程中,其左侧形成膨胀波,并且左侧运动使活塞左侧的压力和密度下降。图10和图11为活塞左侧密度和压力随距离的变化曲线,可以看出采用网格变形插值方法对激波的抹平很小,能够更好地捕捉激波,并且不同位置的密度和压力计算结果与精确解基本一致,明显优于二阶插值方法得到的计算结果。 图10 活塞左侧密度随距离变化规律Fig.10 Relationship between density on the left side of the piston and distance 图11 活塞左侧压力随距离变化规律Fig.11 Relationship between pressure on the left side of the piston and distance 4.2二维激波反射 以二维激波反射为例,对比不同方法插值结果,验证网格变形插值方法的精度。算例计算条件如下: 1)计算区域无量纲长和高分别为2和1; 2)来流马赫数Ma=2.0; 3)以平板前缘到入射激波与平板交点的距离为参考长度,斜激波与平板的夹角为38.66°; 4)按照Rankine-Hugouiot斜激波公式给定入射激波初始条件; 5)入口边界激波的下方给定来流值,上方则给定波后值;上边界给定斜激波的波后值;出口边界则采用外推的方法;壁面处给定无穿透的滑移边界条件。 采用两套网格进行往复插值,如图12所示。先在细网格上计算得到定常初场,此后每计算2时间步传值到另一套网格,往复传值20次,比较不同方法的插值效果。 图13为y=0.3和y=0.54处压力分布及局部放大图。从图中可以看出,线性插值抹平严重,无法准确捕捉间断;ENO方法及网格变形信息传递方法很好地捕捉到了间断,但ENO方法在波后出现了比较明显的非物理振荡。 (a) 细网格(a) Fine-grid (b) 粗网格(b) Coarse-grid 图13 纵向不同位置压力分布Fig.13 Pressure distribution in different position 本文发展的信息传递方法,克服了常用插值方法引起差分方程相容性变化,导致求解精度降低的问题[12],理论上信息传递精度等于求解流场数值方法的精度。通过理论分析给出了二维条件下网格变形的稳定性条件,并介绍了具体的网格变形方法。利用一维活塞算例和二维激波反射算例进行了精度验证,结果表明,信息传递精度显著优于常用二阶插值精度,为发展高精度信息传递方法提供了基础。 参考文献(References) [1]郭正, 刘君, 瞿章华.非结构动网格在三维可动边界问题中的应用[J].力学学报, 2003, 35(2): 140-146. GUO Zheng, LIU Jun, QU Zhanghua. Dynamic unstructured grid method with applications to 3D unsteady flows involving moving boundaries[J]. Acta Mechanica Sinica, 2003, 35(2): 140-146. (in Chinese) [2]郭正, 谭杰, 刘君.振动矩形机翼非线性绕流数值研究[J]. 国防科技大学学报, 2005, 27(4): 13-17. GUO Zheng, TAN Jie, LIU Jun. A research on the numerical value of the nonlinear flow of the oscillating rectangular wing[J]. Journal of National University of Defense Technology, 2005, 27(4): 13-17. (in Chinese) [3]de Zeeuw D, Powell K G. An adaptively refined Cartesian mesh solver for the Euler equations[J]. Journal of Computational Physics, 1993, 104(1): 56-68. [4]刘君, 徐春光, 董海波.基于流固耦合方法模拟减压器动态特性[J].推进技术, 2014, 35(6): 721-726. LIU Jun, XU Chunguang, DONG Haibo. Numerical analysis of dynamic properties for a pressure relief valve using a method of fluid and structure interaction[J]. Journal of Propulsion Technology, 2014, 35(6):721-726. (in Chinese) [5]李鹏, 高振勋, 蒋崇文.重叠网格方法的研究进展[J].力学与实践, 2014, 36(5): 551-565. LI Peng, GAO Zhenxun, JIANG Chongwen. The progress of the overlapping grid techniques[J]. Mechanics in Engineering, 2014, 36(5): 551-565. (in Chinese) [6]Pärt-Enander E, Sjögreen B. Conservative and non-conservative interpolation between overlapping grids for finite volume solutions of hyperbolic problems[J]. Computers and Fluids, 1994, 23(3): 551-574. [7]Margolin L G, Shashkov M. Second order sign preserving conservative interpolation(remapping) on general grids[J]. Journal of Computational Physics, 2003, 184(1): 266-298. [8]王永健. Arbitrary Lagrangian-Eulerian方法及其关键技术研究[D].南京:南京航空航天大学, 2008. WANG Yongjian.Research on Arbitrary Lagrangian-Eulerian method and its key technology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. (in Chinese) [9]王永健, 赵宁, 王春武, 等.ENO守恒插值(重映) 方法及其在流体计算中的应用[J].计算物理, 2008, 25(6): 641-648. WANG Yongjian, ZHAO Ning, WANG Chunwu, et al. Conservative interpolation (remapping) algorithm based on ENO interpolation and application in computational fluid dynamics[J]. Chinese Journal of Computational Physics, 2008, 25(6): 641-648. (in Chinese) [10]张宇飞, 陈海昕, 符松.基于高阶守恒重映对窗口嵌入技术的改进[J].计算物理, 2011, 28(2): 167-173. ZHANG Yufei, CHEN Haixin, FU Song. Improvement on window embedment technology with high order conservative remapping[J]. Chinese Journal of Computational Physics, 2011, 28(2): 167-173. (in Chinese) [11]徐春光.爆炸流场与建筑物结构作用过程数值模拟算法及应用研究[D].长沙: 国防科学技术大学, 2012. XU Chunguang.Numerical simulation algorithm and application research for the interaction of explosion field and the building[D]. Changsha: National University of Defense Technology, 2012. (in Chinese) [12]刘君, 白晓征, 郭正. 非结构动网格计算方法——及其在包含运动界面的流场模拟中的应用[M].长沙:国防科技大学出版社, 2009: 95-99. LIU Jun, BAI Xiaozheng, Guo Zheng. The algorithm for unstructured dynamic grid with moving boundary[M]. Chansha: National university of Defense Technology Press, 2009: 95-99.(in Chinese) [13]Liu J, Bai X, Guo Z, et al. A new method for transferring flow information among meshes[J]. Computational Fluid Dynamics Journal, 2007, 15(4): 509-514. [14]王巍.有相对运动的多体分离过程非定常数值算法研究及实验验证[D].长沙: 国防科学技术大学, 2008. WANG Wei. Numerical simulation technique research and experiment verification for unsteady multi-body flow field involving relative movement [D]. Changsha: National University of Defense Technology, 2008. (in Chinese) [15]Liu Y, Guo Z, Liu J. RBFs-MSA hybrid method for mesh deformation[J]. Chinese Journal of Aeronautics, 2012, 25(4): 500-507. [16]Liu X, Qin N, Xia H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423. New method for transferring flow information among meshes based on mesh deformation DONG Haibo, XU Chunguang, LIU Jun (School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China) According to the data interpolation problems between the old and new grid in the mesh reconstruction, a flow field information transmission algorithm based on the lattice format supported finite volume method was proposed. In order to realize information transfer between the two sets of the grid, the old cells were moved to the new grid cells by using the unstructured dynamic grid technology and the control equation was solved in time domain, then the datum was assigned to the new grid cells. Result shows that the interpolation error is not introduced in the process of information transmission, the theory precision of the method is equal to the precision of information transmission, and the verification results show that the proposed method is significantly better than that of the second order interpolation method. data interpolation; radial basis functions; moving mesh; mesh reconstruction 10.11887/j.cn.201604004http://journal.nudt.edu.cn 2015-04-02 国家自然科学基金资助项目(11272074);辽宁省自然科学基金资助项目(201202033) 董海波(1986—),男,内蒙古赤峰人,博士研究生,E-mail:donghaibo@mail.dlut.edu.cn;刘君(通信作者),男,教授,博士,博士生导师,E-mail:liujun65@dlut.edu.cn O354 A 1001-2486(2016)04-021-07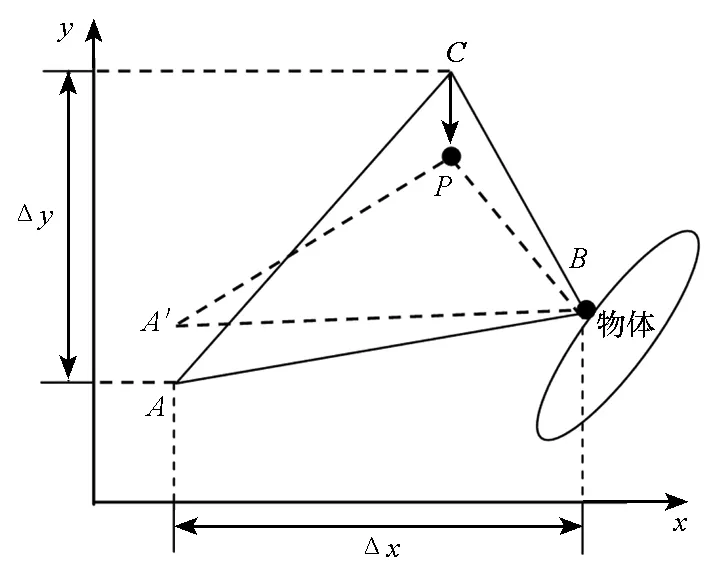
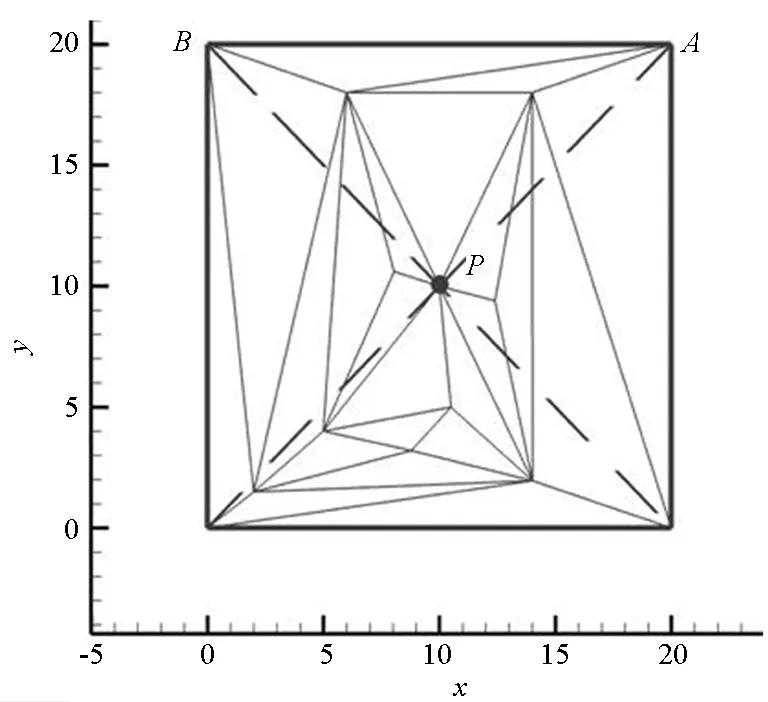
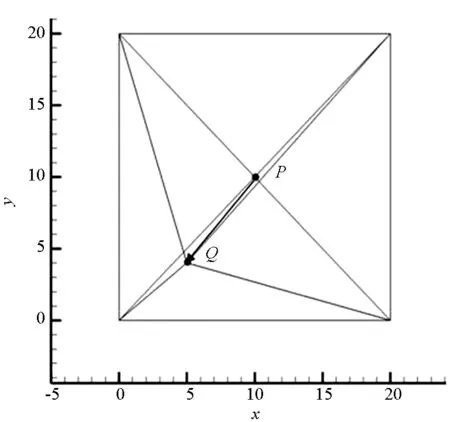
3 网格变形实现方法

4 算例验证

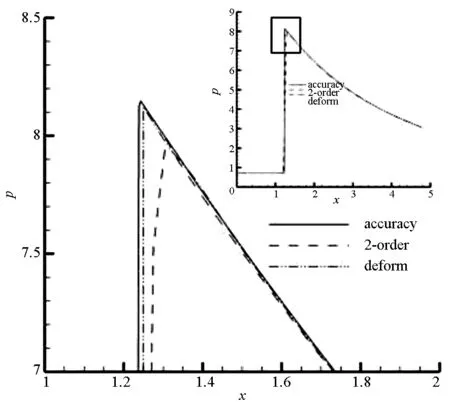


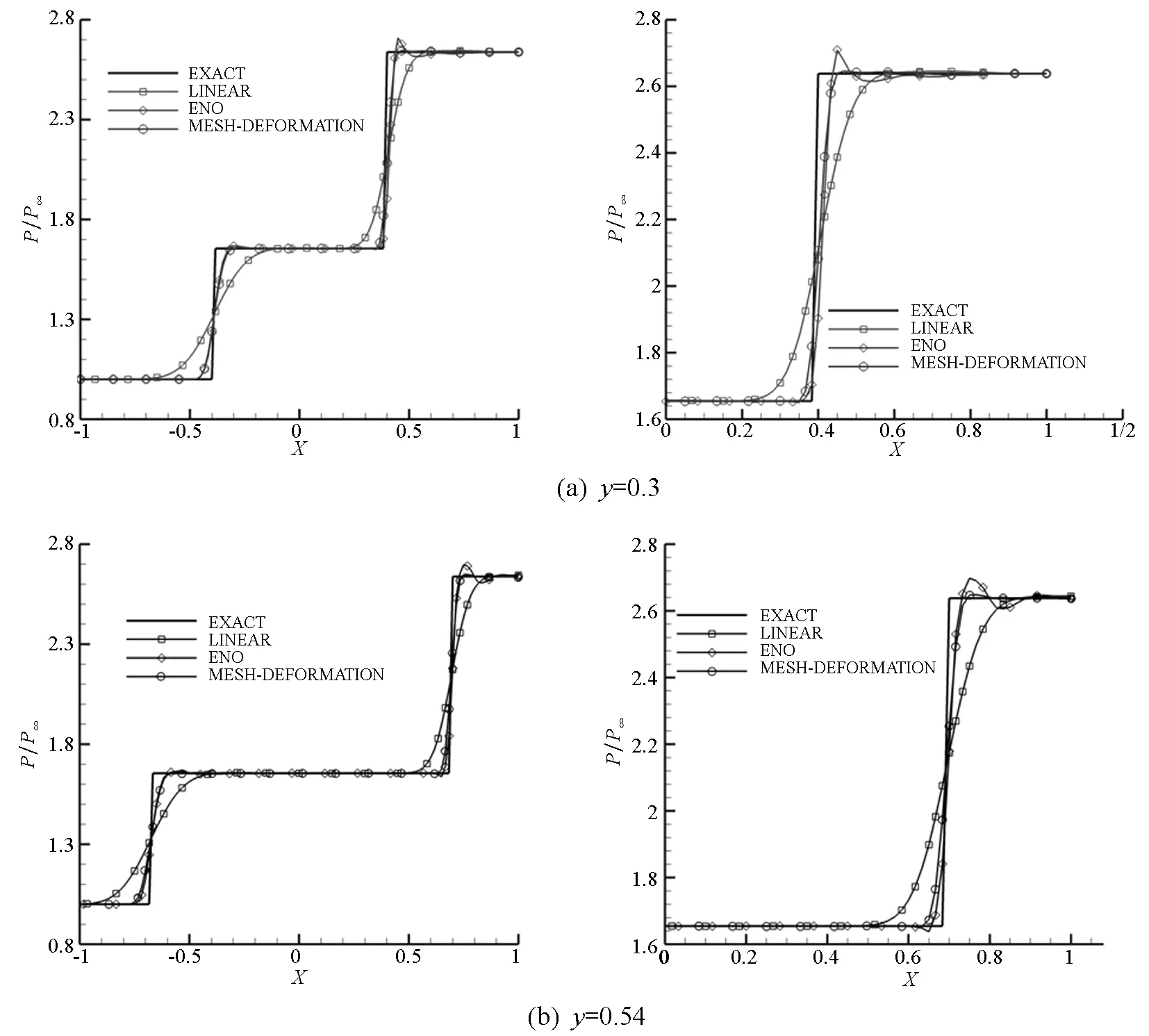
5 结论

