应用加权紧致非线性格式的VFE-2钝前缘三角翼转捩模拟*

王光学，王圣业，王东方，邓小刚

(1.国防科技大学 航天科学与工程学院， 湖南 长沙　410073；2.中山大学 物理学院， 广东 广州　510006)



应用加权紧致非线性格式的VFE-2钝前缘三角翼转捩模拟*

王光学1,2，王圣业1，王东方1，邓小刚1

(1.国防科技大学 航天科学与工程学院， 湖南 长沙410073；2.中山大学 物理学院， 广东 广州510006)

为研究前缘转捩对钝前缘三角翼涡结构的影响，采用高阶精度加权紧致非线性格式和γ-Reθ转捩模型对VFE-2中等半径钝前缘三角翼进行数值模拟。将计算结果与试验结果进行详细对比，结果表明：钝前缘三角翼的前缘分离涡发生在翼尖下游，在特定雷诺数下其具体发生位置受转捩因素影响，采用全湍流模型计算会推迟分离，而耦合转捩模型后的计算结果和试验结果吻合良好。运用耦合转捩模型方法，对钝前缘三角翼涡结构随迎角变化进行模拟。计算结果与试验结果吻合，表明在较小的迎角下，前缘不会产生分离诱导涡；随迎角不断增大，分离诱导涡在三角翼后缘附近产生并向上游移动。

转捩模型；三角翼；高精度格式；加权紧致非线性格式；分离诱导涡

现代战斗机和导弹多采用三角翼布局，以获得良好的飞行品质和机动性能。在不大的迎角下，三角翼在上翼面形成前缘分离涡。前缘分离涡能提供涡升力，提高飞行器的气动特性，但同时也使流动变得复杂。

20世纪50年代以来对三角翼气动特性的研究一直持续至今，其中较有影响力的是国际涡流动试验(Vortex Flow Experiment, VFE)。20世纪80年代开展的第一次国际涡流动试验(VFE-1)，主要关注65°尖前缘三角翼构型[1]。该构型产生“典型”的涡结构，包括起支配作用的主涡和弱的二次涡。对尖前缘三角翼构型的数值模拟也同时发展。早期，代数湍流模型以及低阶精度数值方法，无法较好模拟该类流动。而近年来随着一方程和二方程湍流模型尤其是高精度数值方法的发展，尖前缘三角翼流动已能够被很好地模拟[2-3]。

随着高超声速飞行器的研制，钝前缘三角翼受到广泛关注。钝前缘三角翼的涡结构不同于尖前缘，分离点在翼尖下游某处，其具体位置受多种因素影响，包括雷诺数、迎角和前缘半径等[4-5]。2001年Hummel[6]提出开展第二次国际涡流动试验(VFE-2)，其主要目的之一就是为钝前缘三角翼的计算提供准确的验证数据。近年来，以该试验为依据，国际上许多学者对65°钝前缘三角翼构型开展了数值模拟研究。Schutte[7]基于TAU代码，采用单方程(Spalart-Allmaras, SA)模型和Wilcoxk-ω模型对该构型进行了数值计算，并表明SA模型比k-ω模型更接近试验值；Fritz[8]基于FLOWer代码，采用了SA模型、Wilcoxk-ω模型和雷诺应力模型(Reynolds Stress Model, RSM)模型，而结论却与前者相反，即k-ω模型较好；Crivellini等[9]对比两者结果，发现很难找出造成两者结论相反的因素是湍流模型还是数值方法，并指出应该采用高阶精度数值方法以尽量避免数值方法带来的不确定因素。另外，钝前缘三角翼前缘分离涡的形成常常伴随转捩的发生。Fritz[8]采用固定转捩技术成功模拟了钝前缘三角翼涡结构，但转捩位置固定使该方法具有很大的局限性。

1　高精度数值模拟方法

1.1计算模型

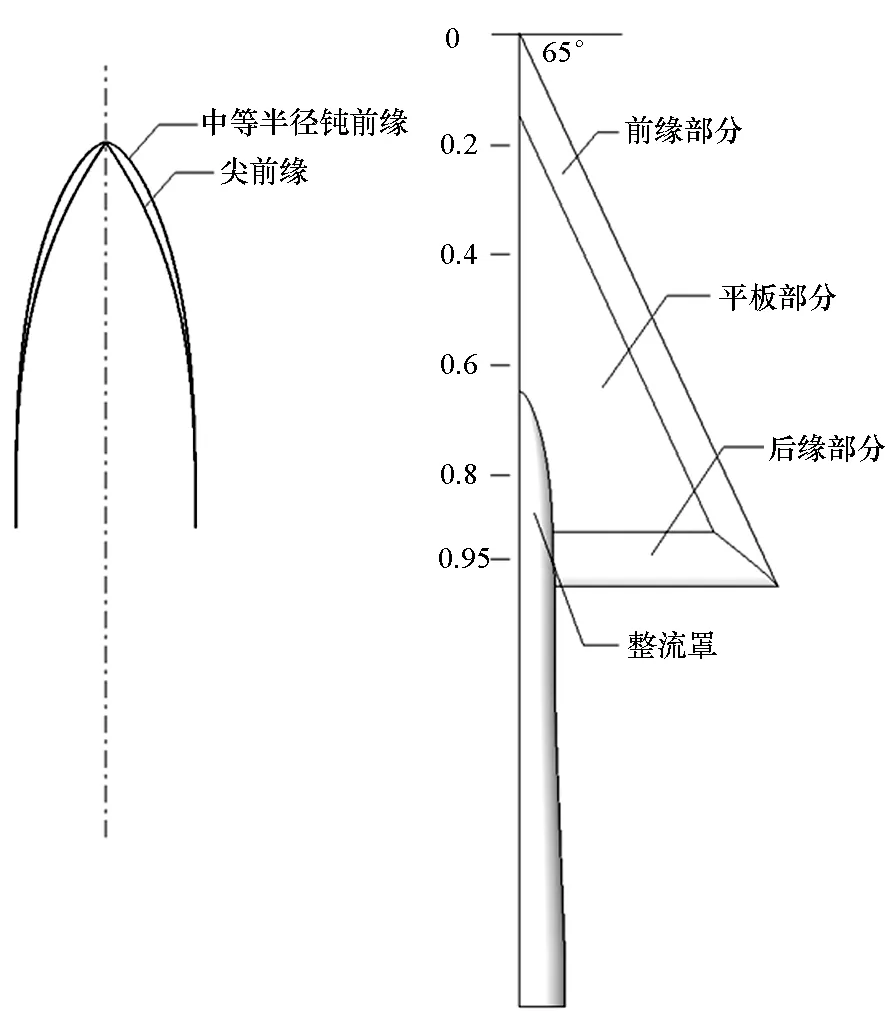
图1　VFE-2三角翼模型Fig.1　Model configuration of VFE-2 delta wing

采用VFE-2 65°后掠角三角翼模型。如图1所示，该模型分为4部分：前缘、平板部分、后缘及整流罩[10]。前缘部分提供4种可替换外形，重点关注中等半径钝前缘外形，同时采用尖前缘外形做对比研究。

1.2计算网格

计算网格自主生成，网格节点数约600万，网格结构为多块对接网格，共27块。图2给出了表面网格。网格拓扑采用C-H型，以避免翼尖奇性轴的产生。计算区域的远场边界取为50倍根弦长。壁面的第一层网格达到了1.0×10-6弦长，网格在背风区和各个剪切层附近均进行了适当的加密，以保证分离区、附面层内和剪切层的数值模拟精度。

图2　三角翼计算网格Fig.2　Computational mesh for delta wing

1.3高精度数值方法简介

加权紧致非线性格式(Weighted Compact Nonlinear Scheme, WCNS)首先由Deng等[11]在2000年提出。其后，不同学者[12-14]发展了多种形式的WCNS，并在广泛的流动问题中证明了格式的优势。采用WCNS系列中的一种典型五阶显式离散格式WCNS-E-5。WCNS-E-5由于其低耗散、高鲁棒和优秀的自由流和涡保持特性，被广泛应用于各种实际流动问题的高精度数值模拟中。时间格式方面，均为定常流动，采用隐式上下对称高斯塞德尔(Lower Upper Symmetric Gauss Seidel, LU-SGS)方法。

对于湍流模型，采用Menter′sk-ωSST模型，其守恒形式为：

(1)

(2)

其中源项及系数具体参见文献[15]。

对于前缘转捩问题，采用γ-Reθ模型，其守恒形式为：

(3)

(4)

其中源项、系数以及与SST模型的耦合参见文献[16]。

另外需要指出的是，在计算网格导数及雅克比时，平台中采用了满足几何守恒律的对称守恒网格导数方法(Symmetrical Conservative Metric Method, SCMM)[17]，有利于提高高精度有限差分方法的鲁棒性并减小数值误差。

2　计算结果与分析

2.1尖和钝前缘三角翼涡结构对比

钝前缘三角翼的涡结构与传统尖前缘三角翼的有很大差异。图3为Ma=0.4，Re=6×106，α=13.3°条件下尖前缘和中等半径钝前缘三角翼涡结构对比。计算均采用全湍流模型，时间推进采用LU-SGS方法。图3左侧，尖前缘三角翼展现了典型的分离诱导前缘涡的特点：来流从翼尖开始分离形成主涡，主涡在翼面再附后卷起外侧附着流形成二次涡。图3右侧，钝前缘三角翼涡结构较为复杂。来流流过钝翼尖并未发生分离，随着下游半展长的增加而前缘半径恒定，机翼在流向上变得越来越尖。前缘相对钝度减小，使来流在翼尖下游某处发生分离。

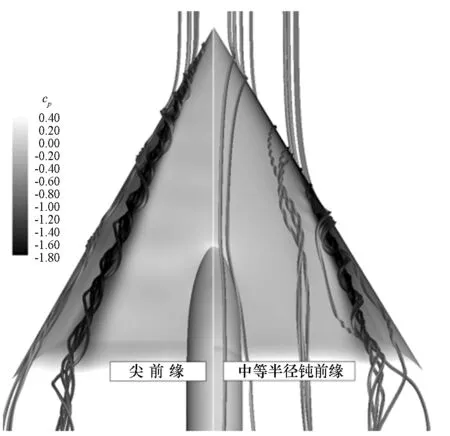
图3　尖和钝前缘三角翼流动对比Fig.3　Contrast of sharp-edge and blunt-edge flows

对于钝前缘三角翼，前缘可被分为3部分：附着区、分离区和过渡区。附着区，来流未发生分离；分离区，来流在前缘分离产生典型的分离诱导涡，并伴随二次涡结构；过渡区，来流在前缘尚未产生分离，但在下游，边界层受逆压梯度(前缘吸力)影响而分离形成内涡，该涡强度较弱，在接近尾缘处受主涡影响而消失。

图4为尖前缘和中等半径钝前缘三角翼典型站位处的压力分布计算值与试验值对比。试验主要在NASA Langley研究中心的LTPT风洞[10]中进行，包括测力和测压试验。在x/cr=0.2处，尖前缘三角翼的吸力峰位于80%当地展长处，即涡核位置，并且计算值与试验吻合很好，而钝前缘三角翼的吸力峰位于驻点处，流动为附着流。在x/cr=0.4处，钝前缘三角翼已产生分离诱导涡，而计算结果中尚未出现吸力峰，即计算的前缘分离点推迟了。在x/cr=0.6处，钝前缘三角翼出现了两个吸力峰，其中内涡强度较弱，位于60%当地展长处；计算结果中同样出现了两个吸力峰，但均比试验结果靠外。在x/cr=0.8和x/cr=0.95处，钝前缘三角翼的内涡强度变得更弱并逐渐消失；而计算的吸力峰仍比试验值靠外。以上典型站位处的压力分布对比表明，采用全湍流模型可以成功模拟尖前缘三角翼涡结构，这与文献[2-3]的结论一致，但在模拟钝前缘三角翼时出现了分离推迟现象。

前缘分离涡可提高机翼上表面吸力，即产生涡升力。而前缘钝度增加会使前缘分离涡推后和减弱。试验测得尖、钝前缘的法向力系数CN分别为0.570和0.517，可以看出，前缘钝度增加将使机翼升力减小。另外，计算所得尖、钝前缘的法向力系数CN分别为0.545和0.461，尖前缘三角翼计算结果和试验值吻合较好，而钝前缘三角翼计算结果偏小，仍是由分离推迟造成。

2.2转捩对钝前缘三角翼涡结构影响

Fritz[8]指出钝前缘三角翼的前缘分离对涡黏性以及数值黏性十分敏感，在采用全湍流模型(包括SAE模型、Wilcox′sk-ω模型和RSM模型)模拟时，均出现了分离推迟的现象。

本节研究Ma=0.4，Re=6×106和α=13.3°条件下，有/无转捩模型对模拟钝前缘三角翼涡结构的影响。图5为有/无转捩模型时三角翼表面压力分布对比。可以看到，不采用转捩模型所计算的分离发生位置比采用转捩模型的明显靠下游，表明了钝前缘三角翼的分离发生位置对于涡黏性十分敏感。

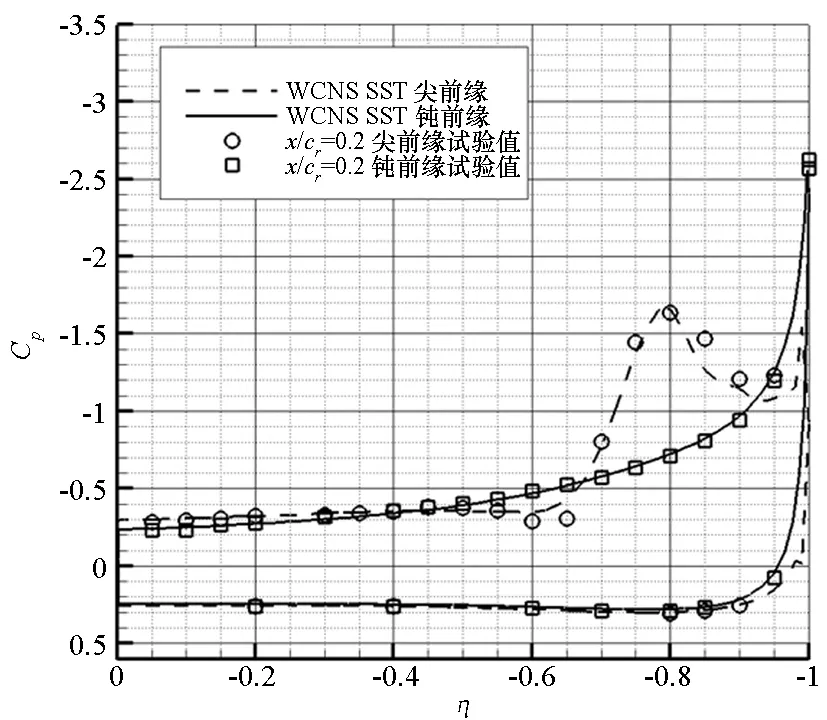
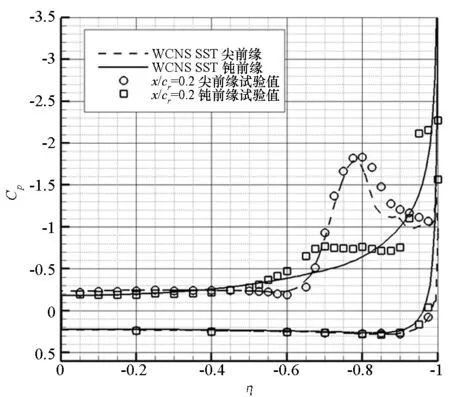
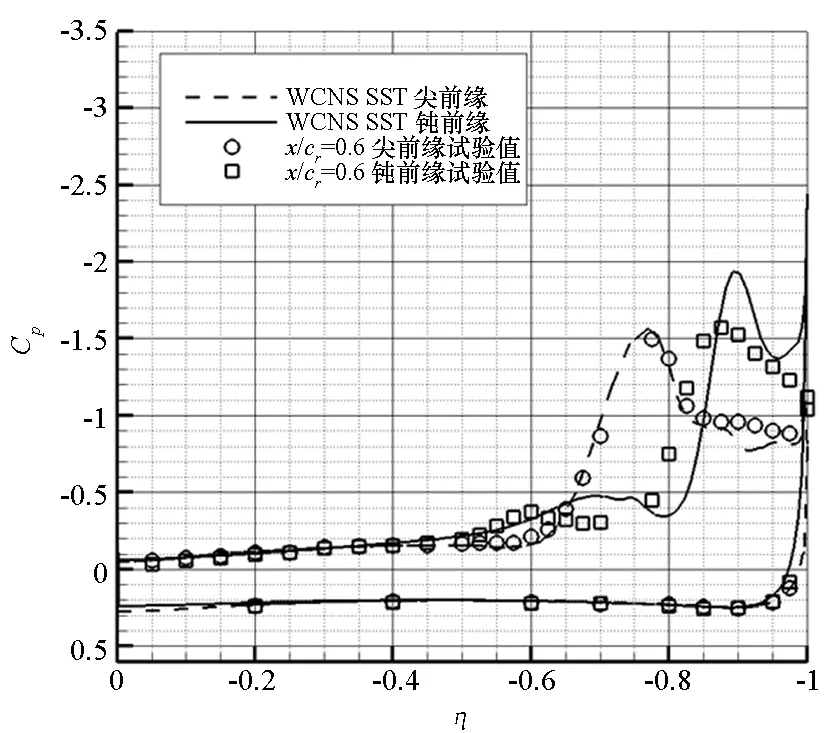
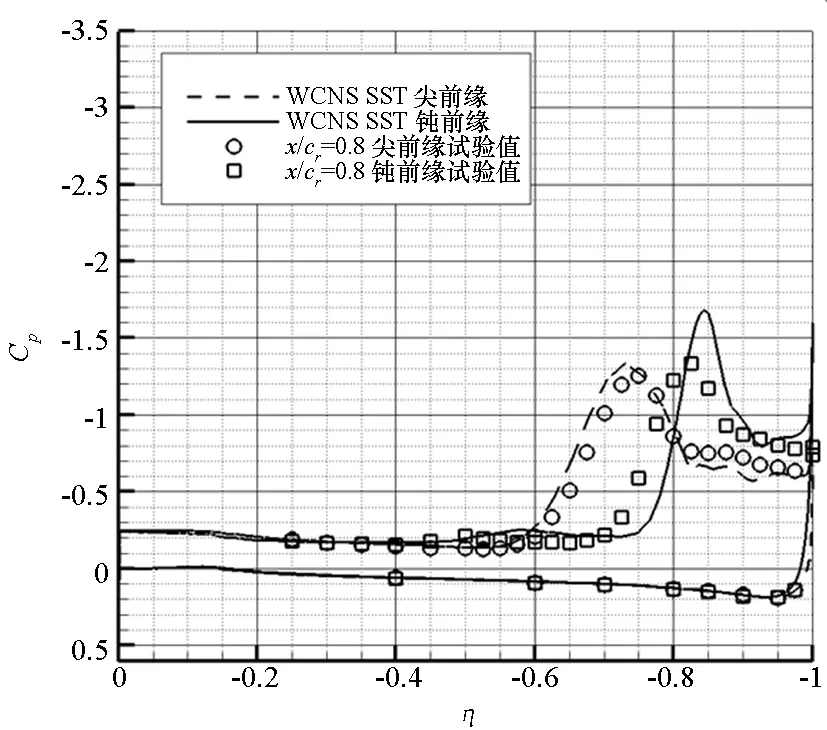
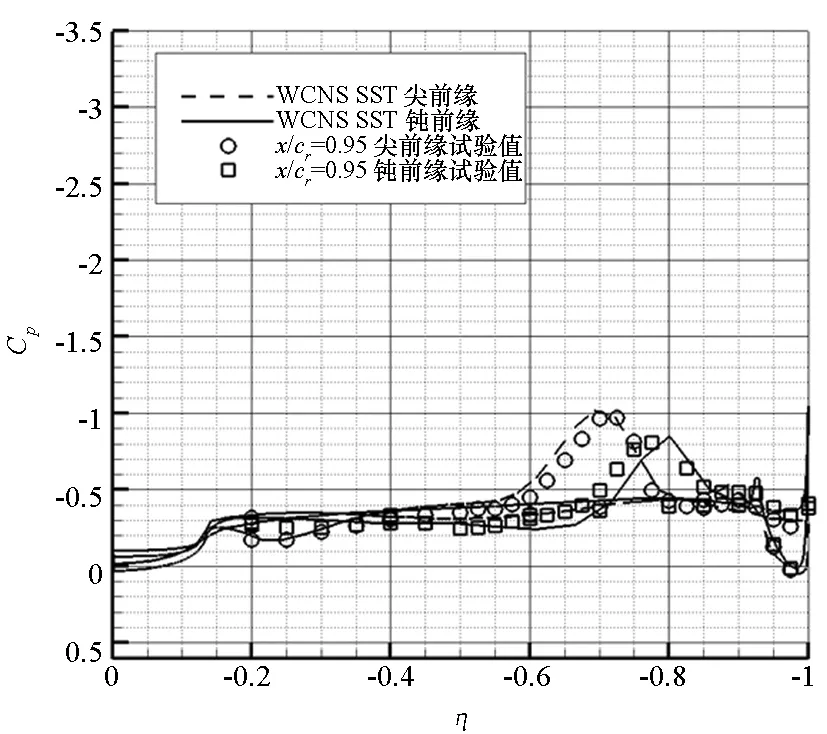
图4　尖前缘和钝前缘三角翼典型站位处表面压力计算值与试验值对比Fig.4　Comparisons of surface pressure with experiments for sharp-edge and blunt-edge delta wing at typical stations

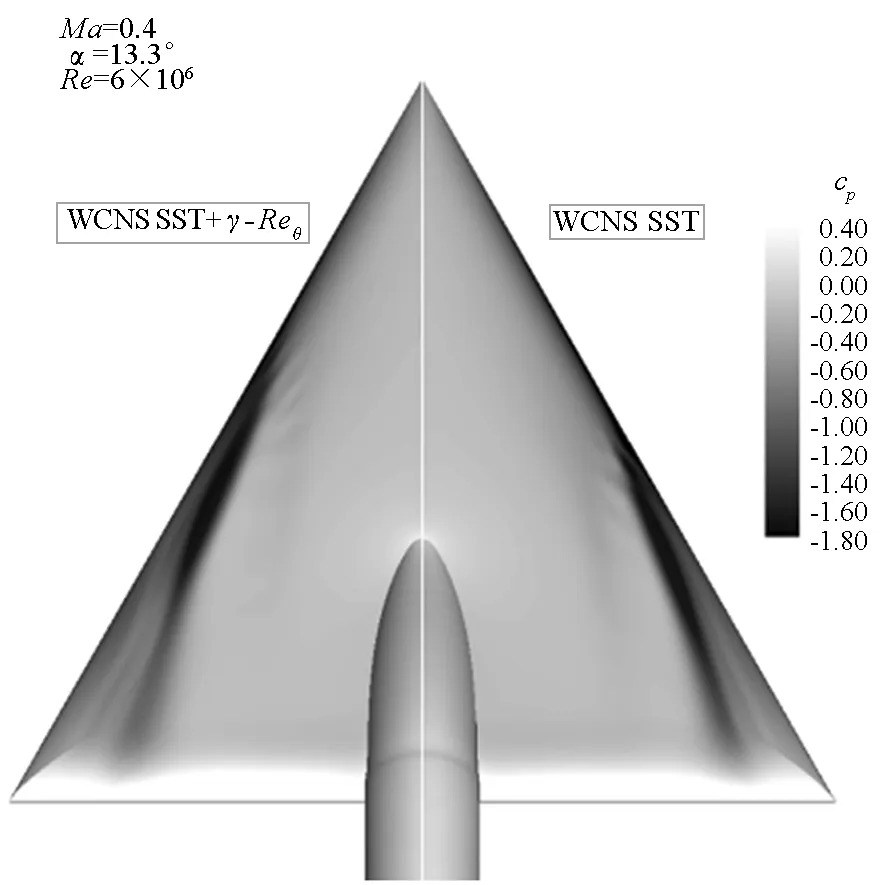
图5　有/无转捩模型三角翼表面压力云图对比Fig.5　Contrast of surface pressure contours of with and without transition model

图6为x/cr分别为0.2，0.4，0.6，0.8和0.95五个典型站位处表面压力计算值和试验值的对比。试验表明，前缘分离涡的起始位置在x/cr为0.2～0.4。在x/cr=0.2处，前缘并未产生分离涡，是否采用转捩模型结果并无差别。在x/cr=0.4处，不采用转捩模型的压力分布中未出现吸力峰，即前缘未发生分离；而采用转捩模型，前缘开始出现分离诱导涡。在x/cr分别为0.6，0.8和0.95三个站位处，采用转捩模型的计算结果和试验吻合很好，而不采用转捩模型，计算的吸力峰靠外。

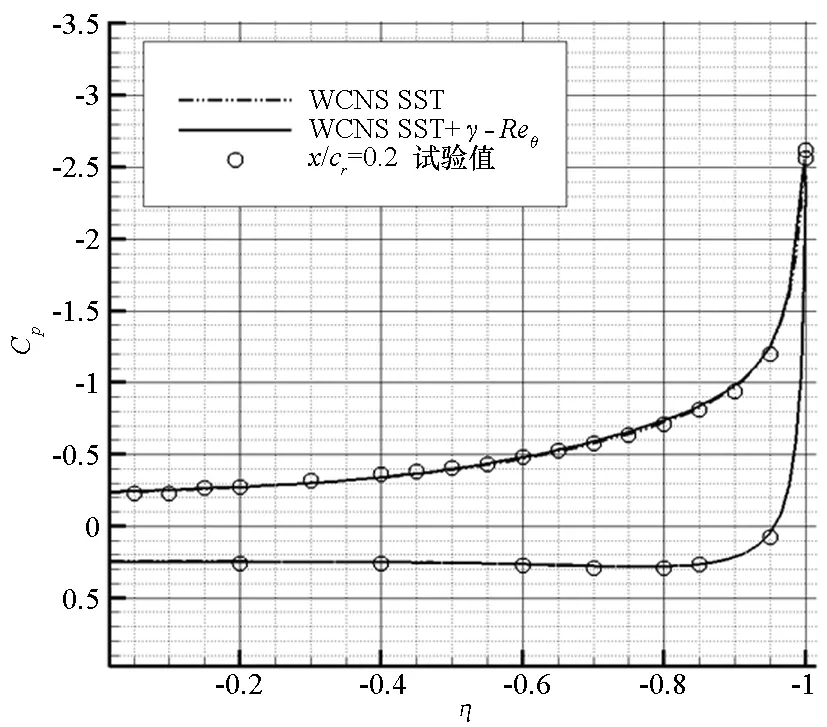
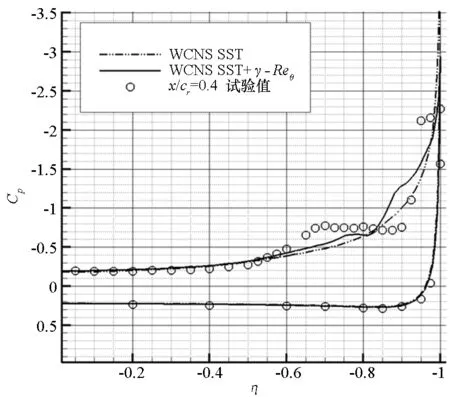
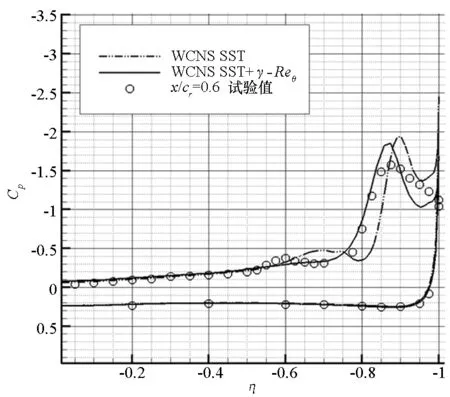
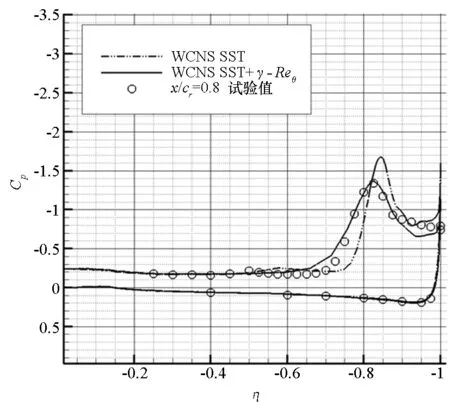
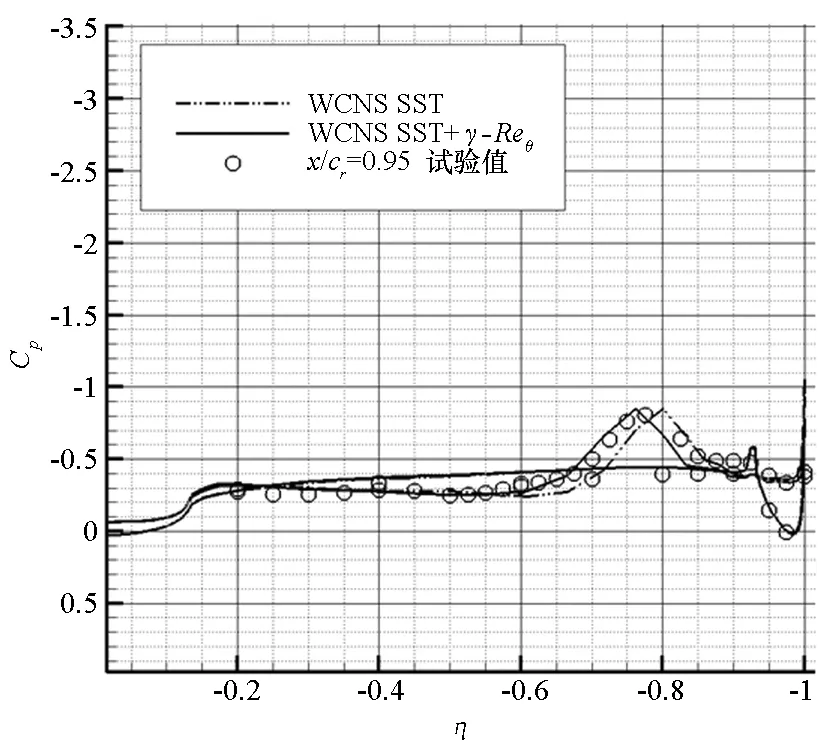
图6　有/无转捩模型，三角翼典型站位处压力分布计算值与试验值对比Fig.6　Comparisons of surface pressure obtained with experiments for blunt-edge delta wing at typical stations of with and without transition model

综合图5和图6表明，基于高精度WCNS，通过耦合转捩模型可很好模拟钝前缘三角翼涡结构，而采用全湍流模型会延迟主涡的发生。分离推迟现象是由于全湍流模型在三角翼前缘层流区高估涡黏性造成的。由于γ-Reθ模型并不模拟实际的物理过程[16]，而相关试验也未研究前缘转捩问题，因此前缘转捩对分离涡影响的物理机理将在今后采用大涡模拟方法进行研究。

2.3钝前缘三角翼涡结构随迎角变化

在特定的来流雷诺数和马赫数下，钝前缘三角翼的分离涡发生位置以及整体涡结构主要受迎角影响。本节采用上节耦合转捩模型的方法，探究钝前缘三角翼涡结构随迎角变化的规律。为与风洞试验对比，计算条件选择：Ma=0.4，Re=3×106，α分别为10.2°，13.3°和15.3°。风洞试验在德国宇航中心的TWG风洞中完成[18]。

图7(a)为WCNS的下转捩模型计算得到的三角翼表面压力分布，图7(b)为试验采用压敏漆技术得到表面压力分布[18]。计算结果与试验符合得很好。在迎角为10.2°时，整个三角翼前缘均为附着流动，并未产生分离诱导涡，仅在接近尾缘处存在较弱的内涡。迎角增大到13.3°时，在x/cr=0.4附近前缘流动出现分离，并形成较强的分离诱导涡。迎角继续增大到15.3°时，前缘分离点提前至x/cr=0.2附近。对于中等半径钝前缘三角翼，随着迎角增大，前缘分离诱导涡从无到有，逐渐向上游移动并不断增强，使涡升力逐渐提高。同时计算的法向力系数CN分别为0.336，0.468和0.548，也印证了该结论。

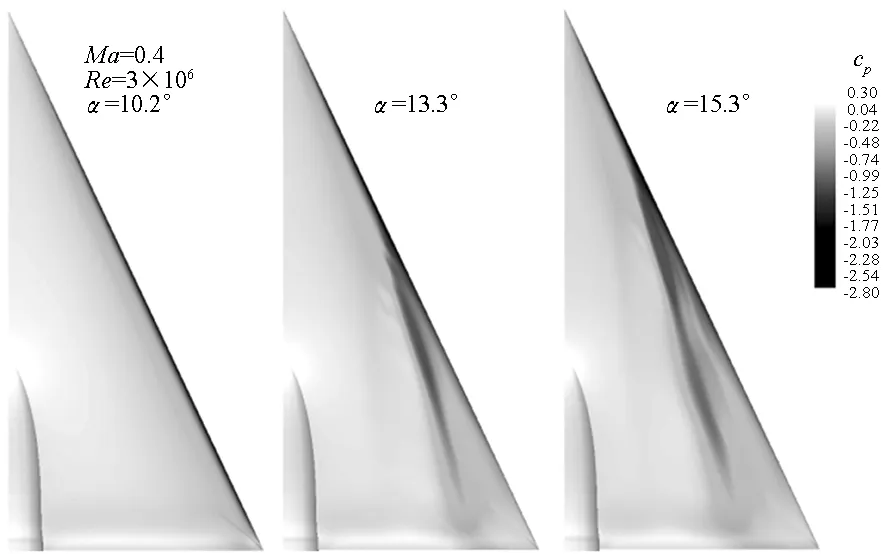
(a) 计算流体力学方法(a) Computational fluid dynamics

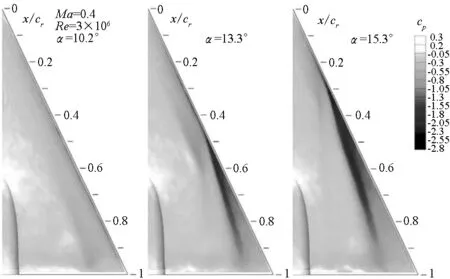
(b) 压敏漆方法(b) Pressure sensitive paint图7　不同迎角下钝前缘三角翼表面压力云图Fig.7　Surface pressure contours of blunt-edge delta wing at variation of the angle-of-attack

3　结论

1)尖前缘三角翼的分离诱导涡发生在翼尖，基于WCNS的全湍流SST模型能很好模拟；钝前缘三角翼的分离诱导涡发生在翼尖下游某处，对涡黏性十分敏感，采用基于WCNS的全湍流模型会出现分离推迟现象。

2) 基于高精度WCNS，在SST湍流模型上耦合γ-Reθ转捩模型，可以很好模拟中等半径钝前缘三角翼的流场。

3) 在特定雷诺数和马赫数下，中等半径钝前缘三角翼的前缘分离涡的产生存在临界迎角。小于该迎角，前缘不会产生分离诱导涡；超过该迎角，分离诱导涡在三角翼后缘附近产生，并随迎角增大而向上游移动，同时法向力也随之增大。

References)

[1]Drougge G.The international vortex flow experiment for computer code validation [C]//Proceedings of ICAS-Proceedings, Jerusalem, 1988, 1: 9-1-9-23.

[2]王光学, 邓小刚, 刘化勇, 等. 高阶精度格式WCNS在三角翼大攻角模拟中的应用研究[J]. 空气动力学学报, 2012, 30(1): 28-33.

WANG Guangxue, DEND Xiaogang, LIU Huayong, et al. Application of high-order scheme(WCNS) at high angles of incidence for delta wing [J]. Acta Aerodynamica Sinica, 2012, 30(1): 28-33.(in Chinese)

[3]王光学, 邓小刚, 王运涛, 等. 三角翼涡破裂的高精度数值模拟[J]. 计算物理, 2012, 29(4): 489-494.

WANG Guangxue, DEND Xiaogang, WANG Yuntao, et al. High-order numerical simulation of vortex breakdown on delta wing [J]. Chinese Journal of Computational Physics, 2012, 29(4): 489-494.(in Chinese)

[4]Luckring J M.Initial experiments and analysis of blunt-edge vortex flows for VFE-2 configurations at NASA Langley, USA [J]. Aerospace Science and Technology, 2013, 24(1): 10-21.

[5]Luckring J M, Hummel D J.What was learned from the new VFE-2 experiments [J]. Aerospace Science and Technology, 2013, 24(1): 77-88.

[6]Hummel D J.The international vortex flow experiment(VFE-2): background, objectives and organization [J]. Aerospace Science and Technology, 2013, 24(1): 1-9.

[7]Schutte A, Ludeke H.Numerical investigations on the VFE-2 65-degree rounded leading edge delta wing using the unstructured DLR TAU-Code [J]. Aerospace Science and Technology, 2013, 24(1): 56-65.

[8]Fritz W.Numerical simulation of the peculiar subsonic flow-field about the VFE-2 delta wing with rounded leading edge[J]. Aerospace Science and Technology, 2013, 24(1): 45-55.

[9]Crivellini A, D′Alessandro V, Bassi F.High-order discontinuous Galerkin RANS solution of the incompressible flow over a delta wing [J]. Computer & Fluids, 2013, 88(1): 663-677.

[10]Chu J, Luckring J M. Experimental surface pressure data obtained on 65°delta wing across Reynolds number and Mach number ranges [R].NASA TM 4645, 1996.

[11]Deng X, Zhang H. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44.

[12]Nonomura T, Fujii K. Effects of difference scheme type in high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2009, 228(10): 3533-3539.

[13]Liu H, Deng X G, Mao M L. High-order behaviors of weighted compact fifth-order nonlinear schemes[J]. AIAA Journal, 2007, 48(8): 2093-2097.

[14]Deng X G, Mao M L, Tu G H, et al. Extending weighted compact nonlinear schemes to complex grids with characteristic-based interface conditions [J]. AIAA Journal, 2010, 48(12): 2840-2851.

[15]Menter F R, Kuntz M, Langtry R B. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, Heat and Mass Transfer 4, 2003: 625-632.

[16]Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamic codes[J]. AIAA Journal, 2009, 47(12): 2894-2906.

[17]Deng X G, Min Y B, Mao M L, et al. Further study on geometric conservation law and application to high-order finite difference schemes with stationary grids [J]. Journal of Computational Physics, 2013, 239: 90-111.

[18]Konrath R, Klein C, Engler R,et al.Analysis of PSP results obtained for the VFE-2 65°delta wing configuration at sub- and transonic speeds [C]//Proceedings of 44th AIAA Aerospace Sciences Meeting and Exhibit, 2006: 60.

Numerical simulation on VFE-2 rounded leading edge delta wing using weighted compact nonlinear scheme

WANG Guangxue1,2, WANG Shengye1, WANG Dongfang1, DENG Xiaogang1

(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China; 2.School of Physics, Sun Yat-sen University, Guangzhou 510006, China)

In order to evaluate the influence of transition on the vortex structure of delta wing, a numerical simulation of VFE-2 rounded leading edge delta wing was carried out by using a high-order scheme-weighted compact nonlinear scheme and theγ-Reθtransition model. A comparisons between calculated results and experiment data indicate that the leading edge vortex begins at a certain distance of the wing apex and the transition has great influence on the onset of leading edge vortex. Using turbulence model without transition, the leading edge separation is delayed much, while with transition model the calculated results show a good agreement with experiment data. With transition model, numerical simulation on VFE-2 rounded leading edge delta wing at variation of the angle-of-attack was carried out. The calculated results which agree well with experiment data show that at a low angle-of-attack, there is no separation-induced leading-edge vortex, but with the increase of angle-of-attack the leading edge separation displays being closer to the trailing edge and moves upstream.

transition model; delta wing; high-order scheme; weighted compact nonlinear scheme; separation-induced vortex

10.11887/j.cn.201604002http://journal.nudt.edu.cn

2016-03-01

国防科学技术大学科研计划资助项目(ZDYYJCYJ20140101)

王光学(1976—)，男，重庆忠县人，博士研究生，E-mail：wgx111@sina.com；邓小刚(通信作者)，男，教授，博士，博士生导师，E-mail：xgdeng2000@vip.sina.com

TN95

A

1001-2486(2016)04-008-06