欠饱和煤储层渗透率动态变化模型及实例分析

吕玉民, 柳迎红, 汤达祯, 李治平

(1.中海油研究总院, 北京　100028; 2.中国地质大学(北京) 能源学院, 北京　100083)



欠饱和煤储层渗透率动态变化模型及实例分析

吕玉民1,2, 柳迎红1, 汤达祯2, 李治平2

(1.中海油研究总院, 北京100028; 2.中国地质大学(北京) 能源学院, 北京100083)

开发过程中因受应力压实效应和基质解吸收缩效应的共同影响，导致煤储层渗透率发生复杂的变化。目前，已有诸多学者建立一系列的煤储层渗透率动态模型。然而，对欠饱和煤层气藏开发过程中的不同生产阶段，何种效应对煤储层渗透率起主导作用仍未达成共识。本研究在总结已有的渗透率变化模型的基础上，分析欠饱和煤层气藏开发过程中的降压解吸特征、有效应力效应、基质收缩效应和克林肯伯格效应，并对现有的渗透率模型进行改进与对比分析，以达到定量分析欠饱和煤层气藏储层渗透率变化规律的目的，最后通过鄂尔多斯东南缘韩城煤层气田实例分析煤储层渗透率动态变化特征及其主控因素。结果表明欠饱和煤层气藏开发过程中渗透率动态变化特征可以临界解吸压力划分为两个阶段，前一阶段仅为有效应力效应作用阶段，后一阶段则受有效应力效应、基质收缩效应和克林肯伯格效应影响，且后两种效应随着储层压力的降低而进一步显现。对比分析显示SD改进模型在描述欠饱和煤层气藏渗透率动态变化上优于PM改进模型。因此，借助SD改进模型对韩城煤层气井进行实例计算，分析结果显示煤储层渗透率改善效果依次为3#>11#>5#，区内煤储层渗透率改善效果取决于含气饱和度，而渗透率应力伤害受控于地解压差。

煤层气藏；欠饱和；动态变化；韩城矿区

0　引　言

煤层气藏开发过程中，煤储层物性受多方面因素的影响而呈现动态变化特征，这些影响因素概括起来主要指有效应力效应[1-9]、基质收缩效应[10-18]和克林肯伯格效应[3, 19-21]。有效应力效应是指在煤层气藏排水降压过程中随储层压力下降，煤层受到的有效应力逐渐增加，进而导致其发生弹塑性变形，使储层物性降低的负效应。基质收缩效应是指当煤层压力低于临界解吸压力后，吸附态的煤层气发生解吸导致煤基质收缩，储层物性得到改善的正效应。另一个正效应为克林肯伯格效应，即指气体通过毛细管壁时沿表面滑移(流动速度不为零)，进而加快气体分子的渗流速度。该效应在低压低渗储层中表现得更为明显。

目前学者对前两个效应在煤层气藏开发过程中渗透率变化的影响研究较为深入，并且建立了多种数学模型[8-23]，但对这两个正负效应在煤层气藏开发过程中的不同生产阶段所起的作用及其影响因素缺乏深入的研究。此外，国内外学者忽略了克林肯伯格效应对低压低渗环境下煤储层渗透率变化的影响。

由于绝大多数煤层气藏为欠饱和煤层气藏，本次研究在分析欠饱和煤层气藏开发特征的基础上，分析其开发过程中渗透率变化规律，并改进现有成熟的渗透率动态变化模型，以实现定量评价欠饱和煤层气藏渗透率动态变化特征。同时，结合鄂尔多斯东南缘韩城煤层气田探井测试分析、测井解释成果等数据，定量计算该气田煤储层渗透率动态变化特征与趋势，并探讨其渗透率动态变化主控因素。

1　开采机理及对其渗透率的影响

煤储层渗透率受有效应力效应[1-9]、基质收缩效应[10-18]和克林肯伯格效应[3, 19-21]三方面因素的共同影响，呈现动态变化的特征。在煤层气开发过程中，有效应力是引起煤储层渗透率下降的惟一效应，属于负效应；而基质收缩效应和克林肯伯格效应则是改善煤储层渗透率并促使渗透率反弹的两个效应，属于正效应。正、负效应的综合作用决定了煤储层渗透率的最终变化趋势。当正效应大于负效应时，煤储层渗透率得到改善，甚至反弹上升；而当负效应大于正效应时，煤储层渗透率则保持下降趋势。

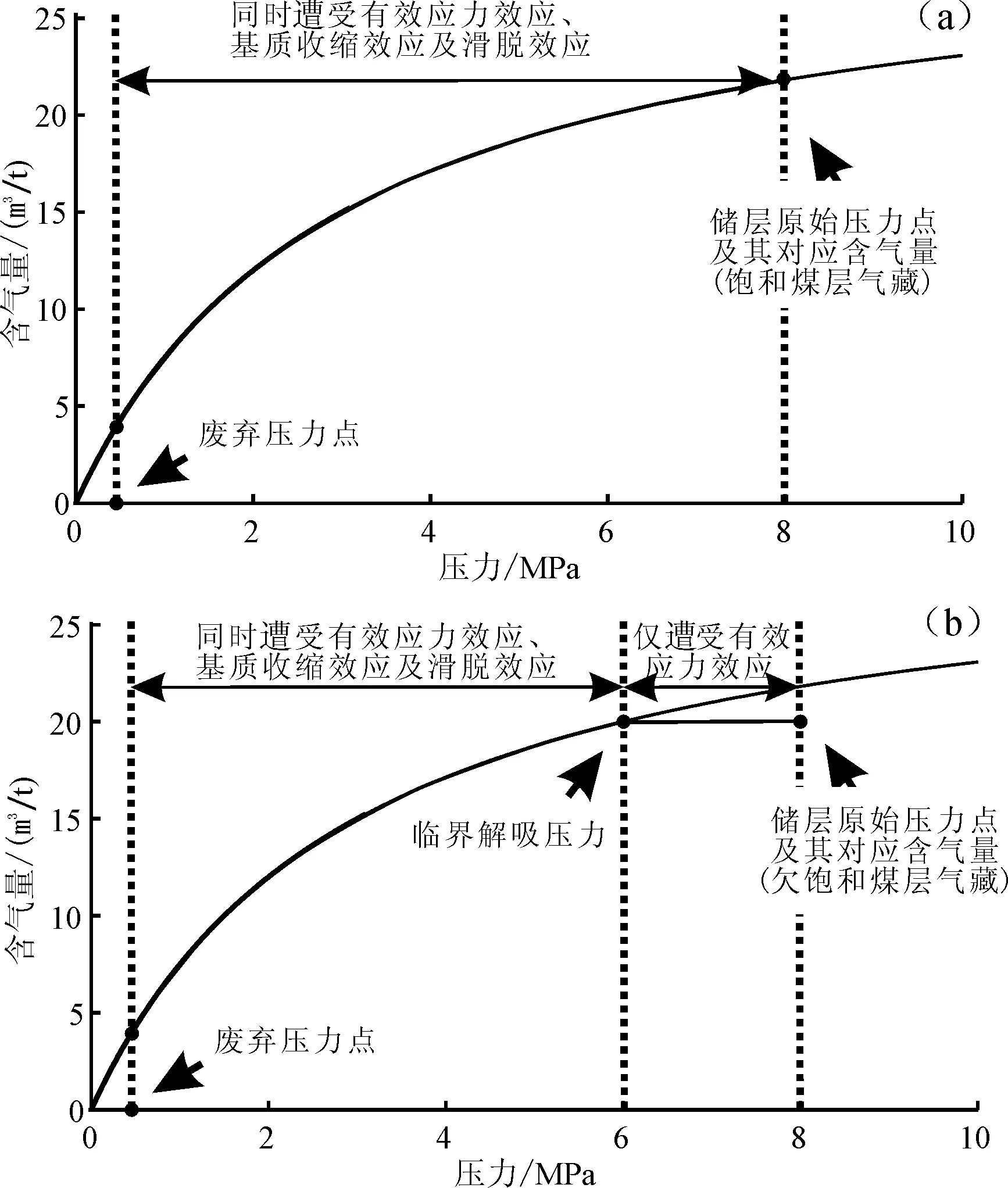
图1　煤层气藏开发机理对渗透率动态变化的控制作用(a)饱和煤层气藏；(b)欠饱和煤层气藏Fig.1　Controls of CBM reservoirs’ development mechanism on dynamic variation of permeability

由于正、负效应发生作用的条件各不相同，必然导致不同煤层气藏及其不同开发阶段影响煤储层渗透率变化的效应也各不相同。对于饱和煤层气藏(图1)来说，由于原始储层压力等于临界解吸压力，从气井开井排水降压时起，储层压力的下降就伴随着发生有效应力效应，引起渗透率下降；同时，另一方面由于储层压力任何幅度的下降，均会引起煤层气发生解吸，进而导致煤基质发生收缩，改善渗透率。这意味着对于饱和煤层气藏的开发，一旦进入开发阶段就同时出现有效应力效应和基质收缩效应。而对于欠饱和煤层气藏(图1)来说，由于原始储层压力大于临界解吸压力，气井开井生产后直至临界解吸压力，煤储层压力的下降均未能引起吸附态的煤层气发生解吸，因此这个阶段内煤储层内部仅发生饱和单相水流，渗透率的变化也仅受有效应力控制；当储层压力降低至临界解吸压力后，吸附态的煤层气才发生解吸，进而才开始出现煤基质收缩效应。因此，可以看出，由于欠饱和煤层气藏与饱和煤层气藏开发过程存在差异，造成煤基质收缩效应出现的阶段也有差异。煤层气藏吸附态饱和度越低，则地解压差(原始储层压力与临界解吸压力之差)越大，煤基质收缩效应往往出现得越晚。此外，与国外煤层相比，我国煤储层具有低渗和特低渗的特征[24-28]，因此煤层气开发过程中不能忽略克林肯伯格效应对煤层气开发过程中影响。

2　常用模型及其改进模型

许多学者提出了大量有关煤储层渗透率的理论模型和经验模型。在这些渗透率模型中，最为广泛应用的主要有Palmer & Mansoori(PM)模型和Shi & Durucan(SD)模型。本次研究针对PM模型和SD模型进行改进，并进行对比优选，使之能更准确地描述欠饱和煤层气藏渗透率动态变化特征。

2.1常用的煤储层渗透率模型

2.1.1PM模型

PM模型是由Palmer和Mansoori于1996年在热力压缩膨胀基础上，建立的煤岩单轴(即垂向)应力条件下的煤储层渗透率变化模型，其公式如下：

(1)式中：cf，基质体积压缩系数，MPa-1；φ0，原始孔隙度，小数；ε，兰氏应变常量，小数；φc，临界解析压力点的孔隙度；K，体积模量，MPa；M，单轴模量，MPa；p，压力，MPa；p0，初始压力，MPa；PL，兰氏压力，MPa。

该模型适合分析单轴应力条件下的应力和基质收缩引起的煤储层渗透率变化，但其仅适用于单组分气体解吸引起的基质收缩效应而导致的渗透率变化。同时，该模型中的孔隙体积压缩系数不是常量，φ变化不能超过30%。

2.1.2SD模型

SD模型类似于PM模型，建立于煤层气解吸引起应力变化而导致渗透率变化的基础上而非引起应变变化而导致渗透率变化的基础上，即煤层气解吸改变体积应变→进而改变水平应力→最终改变储层渗透率。因此，该模型的孔渗变化受水平有效应力引起的垂向割理闭合或开启影响，而不同于PM模型的垂向有效应力引起水平割理闭合或开启。该模型计算公式如下：

(2)

式中：υ，泊松比，小数；E，杨氏模量，MPa。

2.2欠饱和煤储层渗透率模型

2.2.1PM改进模型

基于上述分析，可以看出准确描述欠饱和煤层气藏渗透率变化的PM模型应是分段函数，其分段点为临界解吸压力点。因此，对于原始储层压力降至临界解吸压力时，煤储层渗透率变化仅受有效应力效应的影响；而对于临界解吸压力降至废弃压力时，煤储层渗透率变化同时受有效应力效应、基质收缩效应和克林肯伯格效应的影响，其综合模型表达式为：

(3)

其中引入滑脱系数比：

(4)

式中：pc，临界解吸压力，MPa；φc，临界解吸压力点的孔隙度，小数；bc，临界解吸压力点的滑脱系数，MPa；b，压力p下的滑脱系数。

2.2.2SD改进模型

描述欠饱和煤层气藏渗透率变化的SD模型也是以临界解吸压力点为分段点的分段函数。原始储层压力降至临界解吸压力时，煤储层渗透率变化仅受有效应力效应的影响；而对于临界解吸压力降至废弃压力时，煤储层渗透率变化同时受有效应力效应、基质收缩效应和克林肯伯格效应的影响，其综合模型表达式为：

(5)

3　改进模型可靠性分析

3.1模型参数取值依据

在已建立的改进模型的基础上，借助临界解吸压力之前仅考虑有效应力效应的Seidle模型和临界解吸压力之后仅考虑基质收缩效应和克林肯伯格效应的Seidle-Huitt模型(SH模型)，对PM改进模型和SD改进模型进行可靠性和差异性对比。模型对比分析过程中，各参数的取值范围主要参考国内外已公开发表的数据(如表1)。同时，为了更加准确地评价不同模型的差别，本次研究选取0.2 MPa为废弃压力点进行计算。

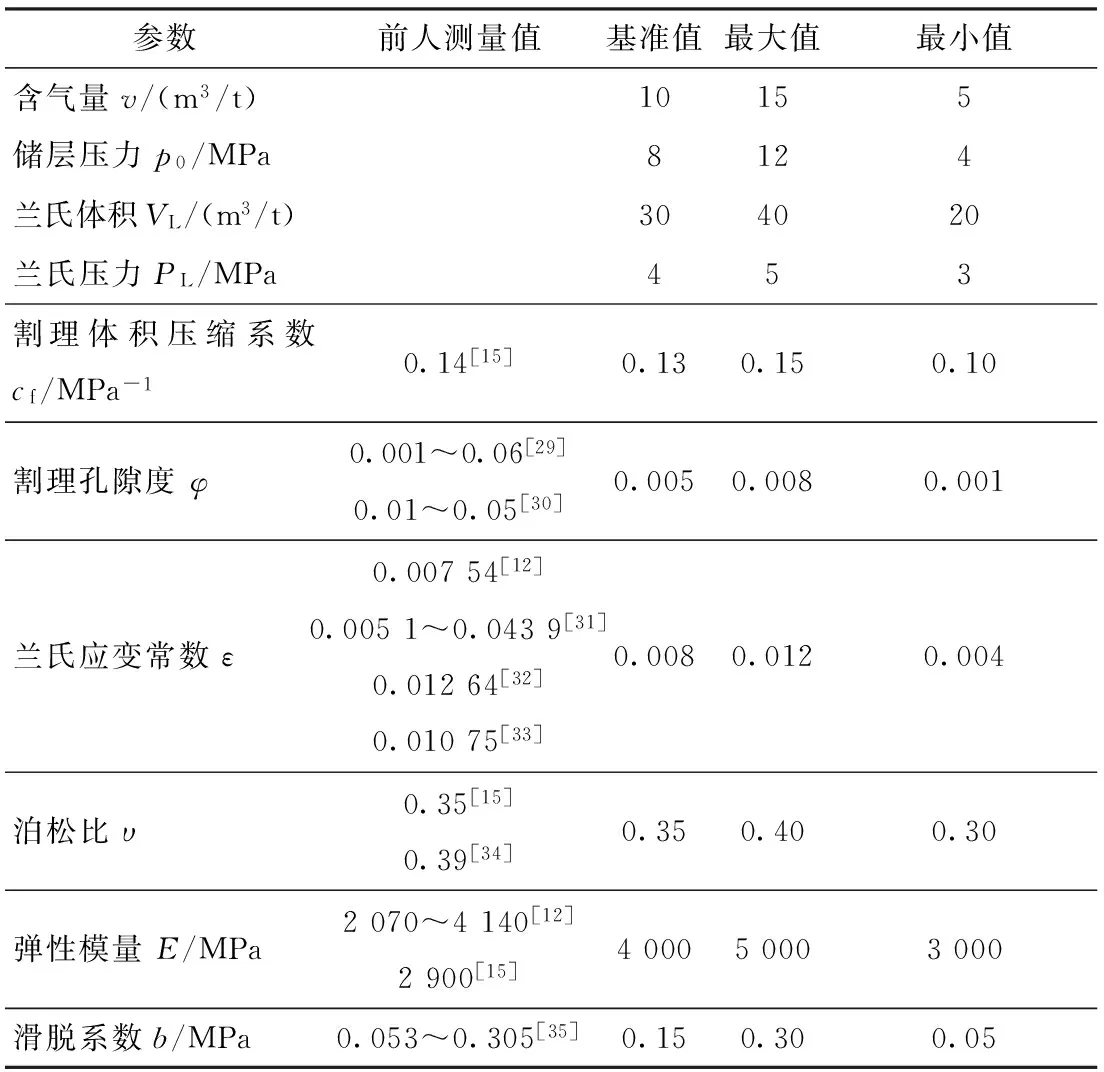
表1　模型参数取值范围

3.2改进模型验证分析

对比改进模型和原模型发现，原模型中的渗透率动态变化明显区别于改进模型。在整个煤层气开发过程中，原模型的渗透率计算值几乎均大于改进模型的(图2)。这主要在于原模型在煤层气开发全过程中考虑了有效应力和基质收缩效应的影响。而在改进模型中，当储层压力高于临界解吸压力时，PM改进模型仅存在有效应力效应，渗透率直线下降，之后随着储层压力降低至临界解析压力之后，基质收缩效应和克林肯伯格效应才发挥作用，并逐渐改善渗透率，最终储层压力降至0.2 MPa时，煤储层渗透率变化值达到2.14(图2)；而PM原模型的渗透率一直呈现缓慢上升趋势。SD模型改进前后的渗透率差异最为明显(图2)，原模型模拟得到0.2 MPa下的渗透率变化值达到11.48，而改进模型模拟得到的仅为5.82。

图2　改进模型可靠性验证对比图(a)改进的PM模型；(b) 改进的SD模型Fig. 2　Reliability demonstration of improved models

造成改进模型与原模型最大的区别在于煤基质收缩效应及克林肯伯格效应影响煤储层渗透率的阶段不同。其中，改进模型是建立在欠饱和煤层气藏开发特征的基础上，考虑到储层压力大于临界解吸压力时，煤储层仅出现有效应力效应，而煤基质收缩效应和克林肯伯格效应则出现在储层压力降至临界解吸压力之下时；而原模型未考虑吸附态煤层气含气饱和度对煤储层渗透率动态效应作用阶段差异性的影响，在整个开发过程中均考虑了有效应力效应、煤基质收缩效应和克林肯伯格效应。

对比PM改进模型和SD改进模型与通用模型(SH模型和Seidle模型)之间的差异性发现，SD改进模型比PM改进模型更接近通用模型(图2)。当处于储层压力大于临界解吸压力的生产阶段，即仅发生有效应力效应，Seidle模型预测的储层渗透率伤害最为严重，储层渗透率伤害80%；PM改进模型储层渗透率应力伤害最弱，仅伤害25%；而SD改进模型计算的储层渗透率变化趋势及其伤害程度均与Seidle模型极为相似，渗透率应力伤害为78%。当处于储层压力低于临界解吸压力的生产阶段，仅考虑基质收缩和气体滑脱的SH模型预测的渗透率最大改善比为5.43，PM改进模型的渗透率最大改善比为2.14，均明显小于通用模型，主要是由于PM模型适用于割理孔隙度变化范围为30%以内的煤储层渗透率预测[13-14]；而SD改进模型的渗透率最大反弹比值为5.82，均略小于通用模型，这主要是由于SD改进模型考虑有效应力效应的影响。对比显示，SD改进模型可靠性更好，更适合分析欠饱和煤储层气藏开发过程中的渗透率变化趋势及其变化量。

4　实例计算与分析

4.1韩城煤层气田基本地质条件

韩城煤层气田位于鄂尔多斯盆地东南缘，区内广泛发育海陆过渡相沉积的太原组和主体为陆相环境沉积的山西组含煤层系，主力可采煤层为3#、5#和11#煤层(表2)，其中3#煤层靠近山西组中下部，北厚南薄，厚度1～2 m，煤层结构较为简单；5#煤层位于太原组上部，局部可采，南厚北薄，厚度1～6 m；11#煤层产于太原组中下部，分布稳定，厚度2～6 m，局部矿区高达10.8 m，结构较为复杂。主力煤层埋深集中在400～1 000 m之间，压力梯度较低，平均仅为8.3 kPa/m，含气量达到8～12 m3/t，兰氏体积集中在20～26 m3/t之间，兰氏压力主要为2.0～2.5 MPa，含气饱和度一般为50%～70%(表2)，属典型的欠饱和低压煤层气藏。

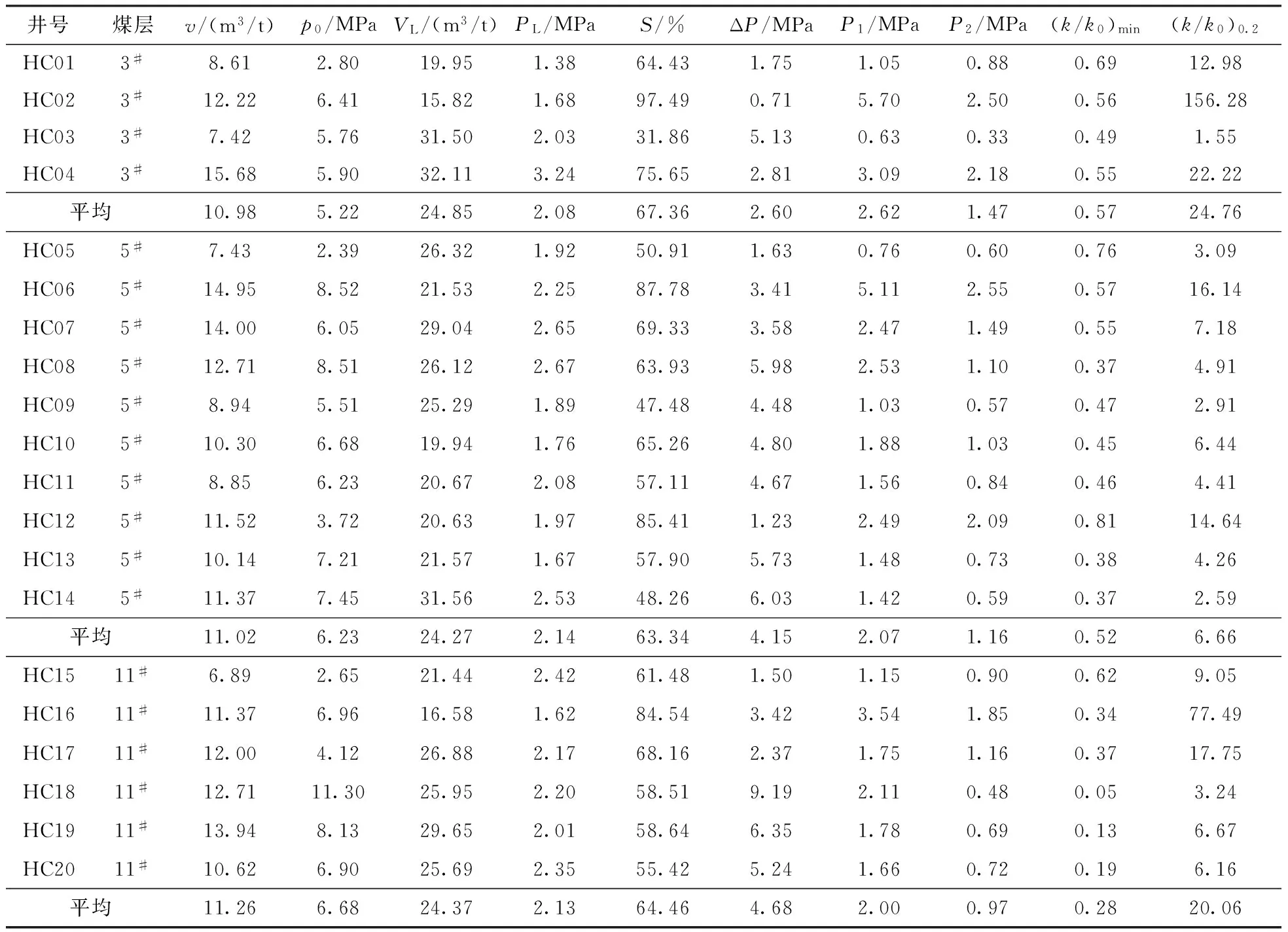
表2　韩城主力煤储层渗透率动态变化统计对比

注：v，含气量；p0，初始储层压力；VL，兰氏体积；PL，兰氏压力；S，煤层气饱和度；ΔP，地解压差；ΔP1，临界解吸压力与废弃压力的差值；P1，k最小点压力；P2，k复原点压力；(k/k0)min，渗透率与原始渗透率之比的最小值； (k/k0)0.2，0.2MPa压力下的渗透率与原始渗透率比值。

4.2韩城主力煤储层渗透率动态对比分析

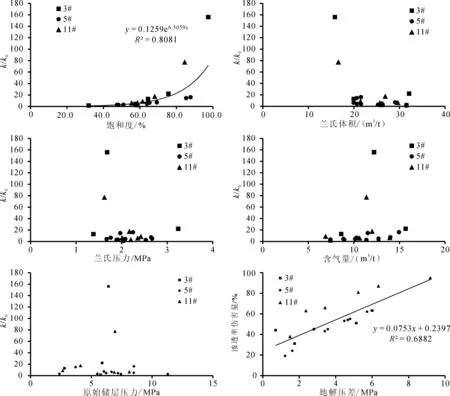
图3　渗透率伤害/改善与影响参数相关性分析Fig.3　Relation analysis of permeability damage and increase with influential factors

研究主力煤储层渗透率变化特征过程中，主要依托探井的含气量、储层压力以及等温吸附参数等测试分析数据，割理压缩系数、割理孔隙度、兰氏应变常数和滑脱系数则以上述表1的基准值为准，而泊松比和弹性模量以测井解释成果为依据。同时考虑到PM改进模型仅适用于割理缝呈水平分布且割理孔隙度变化量不超过30%的煤层，因此，本次对韩城主力煤储层渗透率变化特征的研究仅选取SD改进模型开展相关研究。

从渗透率动态变化趋势看，开发过程中区内主力煤储层间渗透率动态变化特征存在明显的差异性(图3)。其中，3#煤层有效应力效应引起的渗透率伤害最小，平均仅伤害43%，渗透率最终改善效果最好，平均达到24.76；5#煤层有效应力效应引起的伤害较小，平均伤害为48%，渗透率最终反弹改善效果最差，平均仅为6.66；而11#煤层的有效应力效应引起的伤害最为严重，伤害量达到72%，但其渗透率最终改善效果较为理想，平均达到20.06(表2)。

4.3韩城煤储层渗透率动态变化影响因素分析

相关性研究显示影响韩城煤储层渗透率动态变化的主要因素是含气饱和度和地解压差(图3)。影响渗透率最终改善效果的主要因素是含气饱和度，而非兰氏体积、兰氏压力、原始储层压力和含气量(图3)。含气饱和度越大，渗透率改善效果越显著。相同机械力学性质下，煤储层受到的有效应力效应伤害主要取决于地解压差。地解压差越大，煤储层受有效应力效应伤害也越大(图3)，而地解压差受控于吸附态煤层气的含气饱和度；因此，含气饱和度越大，地解压差就越小，煤储层渗透率受有效应力伤害也就越小，有利于储煤层渗透率后期改善反弹的压降幅度也越大，越有利于煤基质收缩和气体滑脱效应充分作用于煤储层，最终煤储层渗透率改善效果也越好，如HC04、HC06和HC16。

5　结　论

(1)在欠饱和煤层气开发机理和现有常用的渗透率模型的基础上，对原有的PM模型和SD模型进行改进，并引入克林肯伯格效应，建立适合于欠饱和煤层气藏的渗透率动态的改进模型。

(2)通过对比研究发现，改进模型比原有模型更适合描述欠饱和煤层气藏的生产规律，更能刻画其煤储层渗透率的变化特征。同时研究显示SD改进模型优于PM改进模型。

(3)实例分析显示韩城地区区内不同煤层以及同一煤层内存在严重的非均质性，其中3#煤层渗透率反弹效果最好，达24.76倍；5#煤层渗透率反弹效果最差；而11#煤层反弹效果居中。

(4)韩城地区煤储层渗透率动态影响因素分析发现，吸附态含气饱和度对渗透率最终改善效果影响最为明显，而地解压差与渗透率应力伤害呈正比。

[1]陈金刚, 徐平, 赖永星, 等. 煤储层渗透率动态变化效应研究[J]. 岩土力学, 2011, 32(8): 2512-2516.

[2]周军平, 鲜学福, 姜永东, 等. 考虑基质收缩效应的煤层气应力场-渗流场耦合作用分析[J]. 岩土力学, 2010, 31(7): 2317-2323.

[3]张春会, 于永江, 岳宏亮, 等. 考虑Klinkenberg效应的煤中应力-渗流耦合数学模型[J]. 岩土力学, 2010, 31(10): 3217-3222.

[4]杨永杰, 宋扬, 陈绍杰. 煤岩全应力应变过程渗透性特征试验研究[J]. 岩土力学, 2007, 28(2): 381-385.

[5]肖晓春, 潘一山. 滑脱效应影响的低渗煤层气运移实验研究[J]. 岩土工程学报, 2009, 31(10): 1554-1558.

[6]汪吉林, 秦勇, 傅雪海. 多因素叠加作用下煤储层渗透率的动态变化规律[J]. 煤炭学报, 2012, 37(8): 1348-1353.

[7]邓泽, 康永尚, 刘洪林, 等. 开发过程中煤储层渗透率动态变化特征[J]. 煤炭学报, 2009, 34(7): 947-951.

[8]GRAY I. Reservoir engineering in coal seams, part 1—the physical process of gas storage and movement in coal seams[J]. SPE Reservoir Engineering, 1987, 2(1): 28-34.

[9]SAWYER W K, ZUBER M D, KUUSKRAA V A. Using reservoir simulation andeld data to dene mechanisms controlling coalbed methane production[M]//CMS. Proceedings of the 1987 Coalbed Methane Symposium. Tuscaloosa: Eastern Region Coalbed Methane Resource Center, 1988: 295-307.

[10]SEIDLE J R, HUITT L G. Experimental measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases[M]//SPE. International Meeting on Petroleum Engineering. Beijing: SPE, 1995: 1-2.

[11]HARPALANI S, CHEN G L. Influence of gas production induced volumetric strain on permeability of coal[J]. Geotechnical and Geological Engineering, 1997, 15(4): 303-325

[12]LEVINE J R. Model study of the inuence of matrix shrinkage on absolute permeability of coal bed reservoirs[M]//GAYER R, HARRIS I. Coalbed Methane and Coal Geology. London: Geological Society Special Publication, 1996: 197-212.

[13]PALMER I, MANSOORI J. How permeability depends on stress and pore pressure in coalbeds, a new model[M]//SPE. SPE Annual Technical Conference and Exhibition. Denver: SPE, 1996:1-2.

[14]PALMER I, MANSOORI J. Permeability depends on stress and pore pressure in coalbeds, a new model[J]. SPE Reservoir Evaluation and Engineering, 1998,1(6): 539-544.

[15]SHI J Q, DURUCAN S. A numerical simulation study of the Allison Unit CO2-ECBM pilot: the effect of matrix shrinkage and swelling on ECBM production and CO2injectivity[M]//MALCOLM W, RUBIN E S. Proceedings of the 7th International Conference on Greenhouse Gas Control Technologies, September 5-9, Vancouver, Canada. London: Elsevier Science, 2004: 431-442.

[16]SHI J Q, DURUCAN S. Drawdown induced changes in permeability of coalbeds: a new interpretation of the reservoir response to primary recovery[J]. Transport in Porous Media, 2004, 56:1-16.

[17]SHI J Q, DURUCAN S. A model for changes in coalbed permeability during primary and enhanced methane recovery[J]. SPE Reservoir Evaluation and Engineering, 2005, 8(4): 291-299.

[18]CUI X, BUSTIN R M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams[J]. AAPG Bulletin, 2005, 89(9): 1181-1202.

[19]CUI X, BUSTIN R M, CHIKATAMARLA L. Adsorption-induced coal swelling and stress, implications for methane production and acid gas sequestration into coal seams[J]. Journal of Geophysical Research-Solid Earth, 2007, 112:1-5.

[20]ROBERTSON E P, CHRISTIANSEN R L. A permeability model for coal and other fractured, sorptive-elastic media[M]//SPE. SPE Eastern Regional Meeting.Canton: Society of Petroleum Engineers, 2006:1-2.

[21]LIU H H, RUTQVIST J. A new coal-permeability model, internal swelling stress and fracture-matrix interaction[J]. Transport in Porous Media, 2010, 82(1): 157-171.

[22]LIU J, CHEN Z, ELSWORTH D, et al. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio[J]. International Journal of Coal Geology, 2010, 83(1): 21-30.

[23]CONNELL L D, LU M, PAN Z. An analytical coal permeability model for tri-axial strain and stress conditions[J]. International Journal of Coal Geology, 2010, 84(2): 103-114.

[24]刘大锰, 姚艳斌, 蔡益栋, 等. 华北石炭系—二叠系煤的孔渗特征及主控因素[J]. 现代地质, 2010, 24(6): 1198-1203.

[25]刘大锰, 姚艳斌, 刘志华, 等. 华北安鹤煤田煤储层特征与煤层气有利区分布[J]. 现代地质, 2008, 22(5): 787-793.

[26]王明寿, 汤达祯, 许浩, 等. 鄂尔多斯盆地东缘煤层气的地质特征[J]. 现代地质, 2005, 19(4): 176-180.

[27]YAO Y B, LIU D M, QIU Y K. Variable gas content, saturation, and accumulation characteristics of Weibei coalbed methane pilot-production field in the southeastern Ordos Basin, China[J]. AAPG Bulletin, 2013, 97(8): 1371-1393.

[28]YAO Y B, LIU D M, TANG D Z, et al. Preliminary evaluation of the coalbed methane production potential and its geological controls in the Weibei Coal field, Southeastern Ordos Basin, China[J]. International Journal of Coal Geology, 2009, 78(1):1-15.

[29]Gas Research Institute. A guide to coalbed methane reservoir engineering[R]. S.l.:Report GRI-94/ 0397, 2002.

[30]MAVOR M J, GUNTER W D. Secondary porosity and permeability of coal: gas composition and pressure[M]//SPE. SPE Annual Technical Conference and Exhibition. Houston: SPE, 2004: 26-29.

[31]ZAHNER R. Application of material balance to determine ultimate recovery of a San Juan Fruitland coal well[M]//SPE. SPE Annual Technical Conference and Exhibition. Texas:SPE, 1997:1-2.

[32]MAVOR M J, VAUGHN J E. Increasing coal absolute permeability in the San Juan basin Fruitland formation[J]. SPE Reservoir Evaluation and Engineering, 1998, 1(3):201-206.

[33]LIU S, HARPALANI S, MALLIKARJUN P. Laboratory measurement and modeling of coal permeability with continued methane production: Part 2- Modeling results[J]. Fuel, 2012, 94, 117-124.

[34]JONES S C. A rapid accurate unsteady-state Klinkenberg parameter[J]. SPE Formation Evaluation, 1972, 12(5):383-397.

[35]TANIKAWA W, SHIMAMOTO T. Klinkenberg effect for gas permeability and its comparison to water permeability for porous sedimentary rocks[J]. Hydrology & Earth System Sciences Discussions, 2006, 3(4):1315-1338.

Permeability Variation Models and Case Studies for Undersaturated Coalbed Methane Reservoirs

LÜ Yumin1,2, LIU Yinghong1, TANG Dazhen2, LI Zhiping2

(1. CNOOC Research Institute, Beijing100028; 2. School of Energy Resources, China University of Geosciences, Beijing100083)

Coal reservoir permeability is under very complicated change due to the combination of the effective stress effect and matrix shrinkage effect during the depletion of reservoir pressure. Nowadays a large number of models have been established to describe permeability variation with the depletion of reservoir pressure. However, no attempt has been made to draw enough attention to the difference of the effect of various factors on permeability variation in different production stages of unsaturated coalbed methane (CBM) reservoirs. This paper summaries the existing and common permeability models, and determines the relationship among various effects (effective stress effect, matrix shrinkage effect and Klinkenberg effect) and desorption characteristics of the recovery of unsaturated CBM reservoirs, then establishes two improved models to describe quantificationally permeability variation by improving the existing models, and finally discusses influence factors on permeability variation with a case study of Hancheng CBM field in Ordos Basin. Results show that the permeability variation during the recovery of unsaturated CBM reservoirs can be divided into two stages: the first one is that the permeability variation is only affected by the effective stress effect, and the second is that the permeability variation is affected by the combination of effective stress effect, matrix shrinkage effect and Klinkenberg effect. In the second stage, matrix shrinkage effect and Klinkenberg effect play much more significant role than effective stress effect, leading to the increase of permeability with depletion of reservoir pressure. A comparative study of the improved models indicates that the improved SD model is more sensitive to various parameters than the improved PM model and the improved models, and can describe dynamic permeability variation more exactly than the original ones. Thus, the case study, by improved SD model, on Hancheng CBM field shows that the increase in coal reservoir permeability is determined by gas saturation, and the damage in coal reservoir permeability is controlled by the difference between the initial reservoir pressure and critical desorbed pressure, and the descending order of the average increment is 3#, 11#and 5#.

coalbed methane reservoir; permeability; dynamic variation; Hancheng mining area

2015-04-25；改回日期：2016-03-27；责任编辑：潘令枝。

国家科技重大专项(2011ZX05034-001，2011ZX05038-001)；国家自然科学基金项目(41272175)；博士后科研基金项目(2014M561020)；中海油科技项目(CNOOC-KY125,YXKY-2015-ZY-08)。

吕玉民, 男, 博士, 1985年出生, 矿产普查与勘探专业，主要从事非常规油气地质与开发研究。Email: lvym@cnooc.com.cn

TE132.2

A

1000-8527(2016)04-0914-08