一种转子动态不对中量计算方法

陈　宏　雷文平　陈　磊　韩　捷

郑州大学，郑州,450001



一种转子动态不对中量计算方法

陈宏雷文平陈磊韩捷

郑州大学，郑州,450001

从运动学角度出发，分析了双跨转子系统的运动特性和运动形态，提出了一种转子动态不对中量的定量计算方法。该方法通过安装在转子系统上的电涡流传感器获得转子运动的轴心位置信息，根据相似三角形定理，计算获得两根转子在联轴器处的轴心平动位移和角位移，再根据矢量合成法则，即可获得两根转子在联轴器处的平行不对中量以及角度不对中量。工程实践表明，该方法确定的不对中故障类型与特征典型的不对中故障类型表现出的时域波形特征、频谱特征以及轴心轨迹特征一致。该方法不但能够准确地诊断不对中的种类，而且能够得到不对中的定量结果，为工程实际中不对中故障的处理及轴系对中提供了量化参考。

不对中;定量分析;故障诊断;旋转机械

0　引言

不对中是旋转机械中最常见的典型故障之一，仅次于不平衡位于第二位[1]，据资料统计，旋转机械中有60%的故障与不对中有关[2]。不对中故障能够产生附加作用力，从而引起设备的振动、轴承的磨损、油膜失稳、转子弯曲变形等，对设备的安全运行危害极大[3]。不对中故障一般分为轴承不对中和联轴器不对中两大类，其中联轴器不对中又可分为平行不对中、角度不对中和平行角度不对中三种情况，轴承不对中分为偏角不对中和标高变为两种情况[3]。文献[4]提出了一种新的旋转机械不对中分类形式，即同侧轴承不对中、异侧轴承不对中和混合不对中，并研究了相应的故障机理及振动特征。韩捷[5]从运动学角度研究了齿式联轴节不对中转子的故障物理特性，对其频率特性及产生的激振力进行了详细分析；雷文平等[6]用有限元法研究了齿式联轴节不对中转子的动力学响应，得到了不对中量和稳态响应之间的量化关系及2倍频的相位特性；Sekhar等[7]用有限元法研究了联轴器不对中对旋转机械振动的影响；Jin等[8]研究了带有角度不对中的柔性圆盘的振动特性；Bouaziz等[9]研究了当转子存在偏角不对中时的动力学特性。以上文献均从理论和数值仿真的角度研究了不同类型的不对中对旋转机械的影响，对理解和认识不对中故障的机理和特征具有重要意义。文献[10-11]分别研究了从启停机过程中估计不对中量方法和用扭矩检测联轴器不对中的方法，对工程实际中不对中故障的监测、评估和诊断提供了有效的方法。

尽管学者们对不对中故障产生的机理及其特征进行了大量的研究，并且已经取得了丰富的研究成果[12-16]，然而对不对中故障的认识仍不完全[15]，对于不对中的诊断仍只是以谐波的存在为依据，特别是2倍频几乎成为不对中故障的代名词。但是，其他故障研究也表明，由于非线性因素的存在，有许多故障也会产生较大的2倍频，如裂纹、松动等，而且，不对中故障本身由于联轴器类型的不同、不对中类型的不同、故障严重程度的不同，2倍频有时也不明显，因此2倍频并不是诊断不对中故障的可靠依据。同时，大量文献集中在不对中故障的定性研究，对不对中故障的定量描述很少涉及[15]，由于多种原因，精确对中几乎是不可能实现的[16]，因此，对于工程实际中转子不对中的量化显著尤为重要。

本文针对大型旋转机械，分析了转子运动特性，提出了一种转子动态不对中量的计算方法。

1　双跨转子运动特性分析

1.1双跨转子模型

工程实际中大多数大型旋转机械至少包含两个转子，即一根驱动转子和一根被驱动转子，且支承轴承为滑动轴承，为了简化分析，只考虑径向运动，建立一个双跨转子模型，如图1所示。

图1　双跨转子模型

图1中，Bi(i=1,2,3,4)为支承轴承，D1、D2分别为两根转子上的集中质量，Vi(i=1,2,3,4)为振动测量截面，每个截面上互相垂直布置两只电涡流位移传感器，其中位于左手侧传感器称为x，右手侧传感器称为y。Li(i=1,2,…,10)分别为各轴段长度，C为联轴器。设左边轴为主动轴，右边轴为从动轴，从主动轴向从动轴看，转子逆时针旋转，旋转角速度为Ω。

1.2双跨转子运动形态分析

考察图1所示双跨转子中心线的运动形态，当转子静止时，转子轴中心线位置如图2a所示，当转子在不平衡力作用下以角速度Ω做弓形旋转时，转子中心线的运动形态如图2b所示，图2c为转子某个截面上的动态轴心位置图，其中中间的黑色圆点为轴中心平均位置，椭圆为轴心轨迹。

(a)转子轴中心线位置

(b)转子中心线运动形态

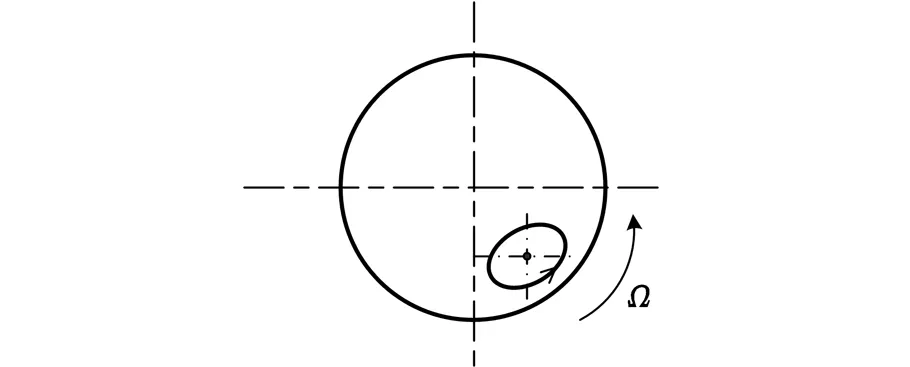
(c)转子动态轴心位置图图2　双跨转子中心线运动形态

图2中，当转子静止时，由于重力的原因，转子轴中心线产生一个静挠度(图2a)，此时，假设转子对中良好，联轴器保持水平状态。当转子以角速度旋转时，在不平衡力作用下，转子做弓形回转，单个转子回转轨迹为纺缍形(图2b)，其某一截面上的轴心轨迹为一椭圆(图2c)，因此，其动挠度曲线的回转中心线(为了简便，简称为回转中心线)为一直线。联轴器除了做弓形回转外，还以其横截面为中心面，作往复摆动，这是一个平面运动。当两个转子对中情况良好时，转子回转中心线在一条直线上，此时没有附加的作用力产生。

2　联轴器动态不对中量计算方法

由上述分析得知，转子做弓形回转时，其回转中心线为一直线，因此，根据两点决定一条直线的定理和相似三角形法则，只要能够获得该转子任意两个截面上的轴心位置，即可确定整个转子的回转中心线，也就能够确定联轴器处的轴心位置，两根转子在联轴器处的轴心位置差就是联轴器的动态不对中量。

图3给出了联轴器不对中时转子轴中心线的运动形态示意图，图中Δ为联轴器动态平行不对中量的大小，Φ为平行不对中量与x轴的夹角，Ψ为两转子回转中心线的角度不对中量，Ψx、Ψy分别为Ψ的投影角。结合图1，推导此时联轴器的不对中量计算公式。

(a)联轴器不对中转子轴中心线运动形态

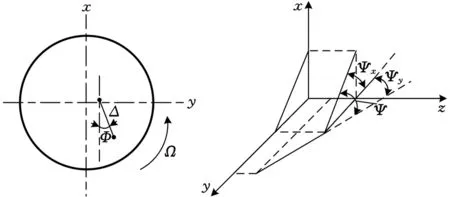
(b)平行不对中量　　　　　　(c)角度不对中量　图3　不对中时转子轴中心线运动形态示意图

图4给出了静止时和旋转时两转子轴中心线的瞬时位置，其中虚线为静止时的轴中心线位置，实线为旋转时的轴中心线位置，dij(i=1,2,3,4,L,R;j=x,y)分别为测量截面和联轴器处的轴心位置在传感器方向上的变化量。θx、θy、φx、φy分别为两根转子的动态回转中心线与静态时回转中心线在x、y方向的夹角。

(a)x方向不对中量计算示意图

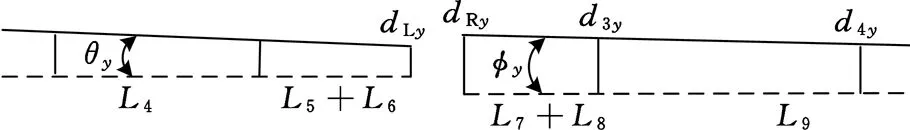
(b)y方向不对中量计算示意图图4　不对中量计算示意图

根据相似三角形定理，有

(1)

(2)

(3)

(4)

由式(1)～式(4)可得，联轴器不对中量为

(5)

(6)

3　工程应用

某燃气电厂一台39MW燃气发电机组如图5所示，该机组由燃气轮机、发电机、SSS离合器、汽轮机(分中低压缸、高压缸两部分)组成，共有8套径向支承轴承(分别标为1～8)支承，轴承跨距如图5所示。每套轴承处均安装有互相垂直的电涡流传感器(图中P1～P8)监测机组的轴振动，C1、C2为两个联轴器。

图5　某燃气发电机组结构简图及测点布置图

由图5可知，发电机转子与汽轮机高压缸转子之间由一个SSS离合器和一个联轴器进行连接，且汽轮机中低压转子和高压转子为两根转子三支承结构，它们之间的对中情况较为复杂，为了验证本文提出的新方法，只考虑燃气轮机转子与发电机转子的不对中情况。

表1给出了测点P1～P4轴心位置变化值，表2所示为根据式(5)和式(6)计算出的联轴器C1的动态不对中量，表3为测点P1～P4的振动值，表中“通频”指的是直接来自于测试系统的满足采样定理要求的原始信号，未经过其他滤波处理，是全频带的信号，1X和2X分别指的是转频的1倍频和2倍频，均计算的是峰峰值(P-P值)。

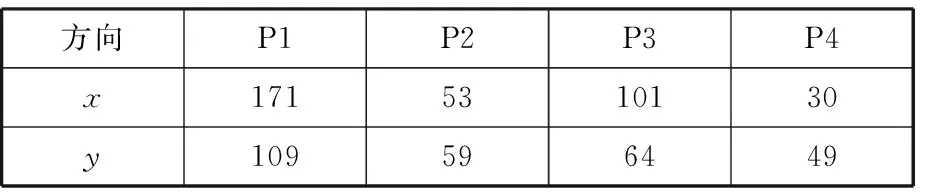
表1　P1～P4轴心位置变化值　μm

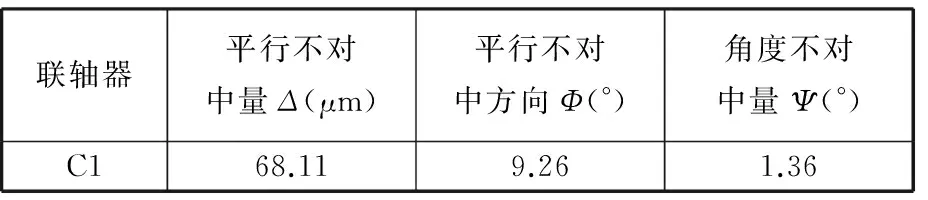
表2　联轴器C1不对中量

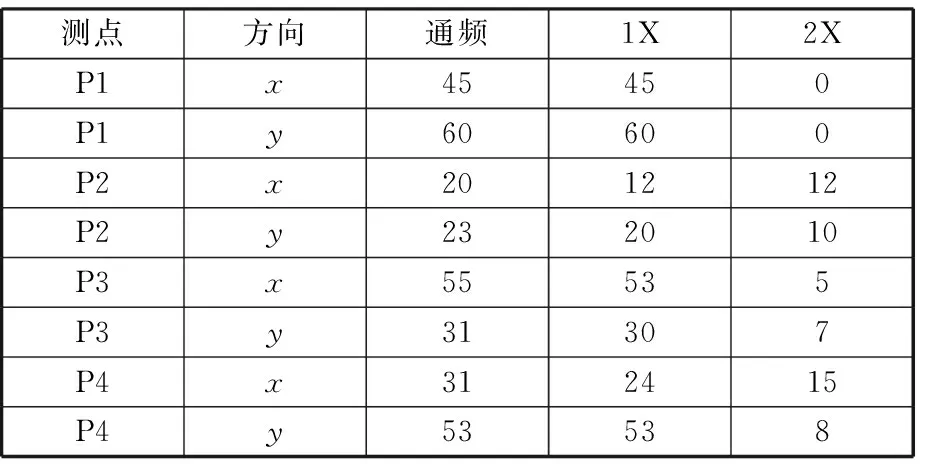
表3　测点P1～P4振动值　μm

根据表2可以看出，联轴器不对中主要表现为平行不对中，角度不对中很小，可以忽略不计。对比表3测点P1～P4的振动值，测点P1仅有1X分量，没有表现出不对中特征，而联轴器两侧测点P2和P3均表现出一定的不对中特征，特别是测点P2，x方向的2X分量占通频值的60%，y方向的2X分量占通频的50%，表现出明显的平行不对中特征，而测点P3尽管也有2X分量存在，但占通频振动的比重较小，这可能与发电机转子还受SSS离合器和汽轮机转子的约束有关。图6～图8分别给出了测点P2、P3的时域波形、幅值谱和轴心轨迹。

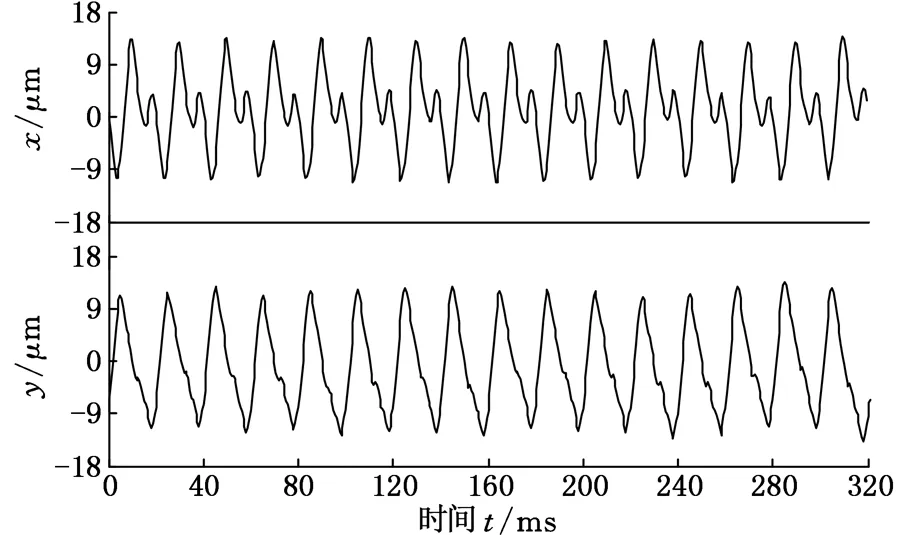
(a)测点P2在x、y方向的时域波形图

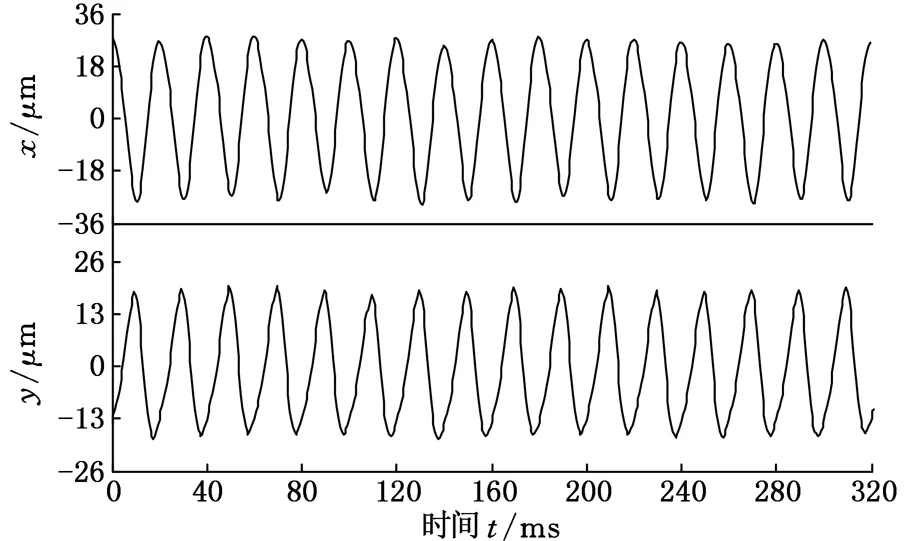
(b)测点P3在x、y方向的时域波形图图6　测点P2和P3的时域波形图

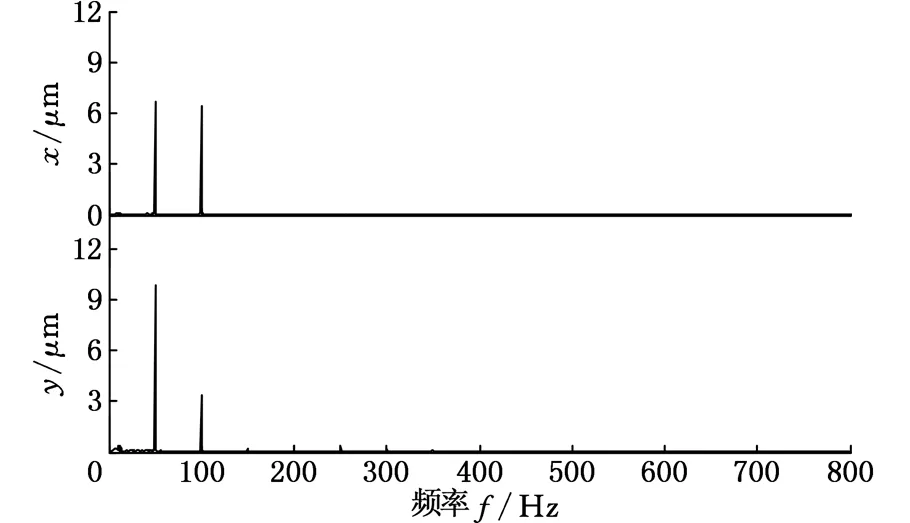
(a)测点P2在x、y方向的幅值谱图

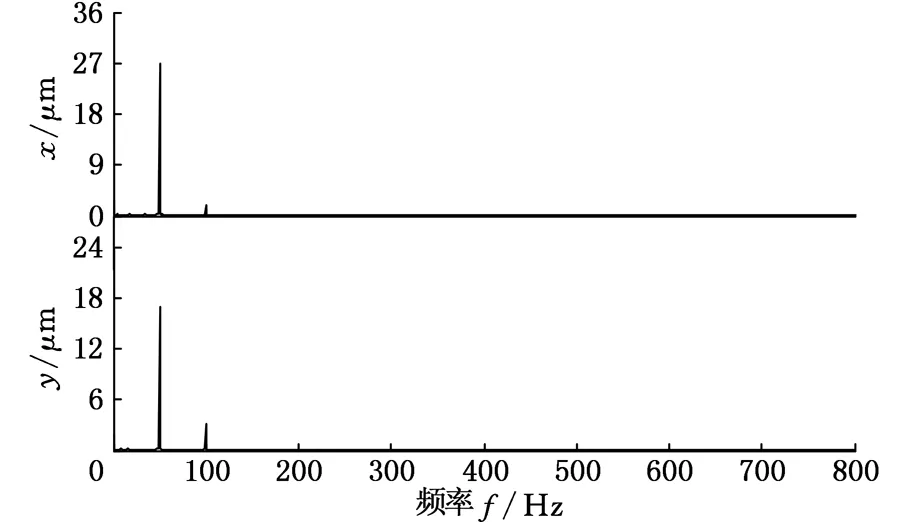
(b)测点P3在x、y方向的幅值谱图图7　测点P2和测P3幅值谱图

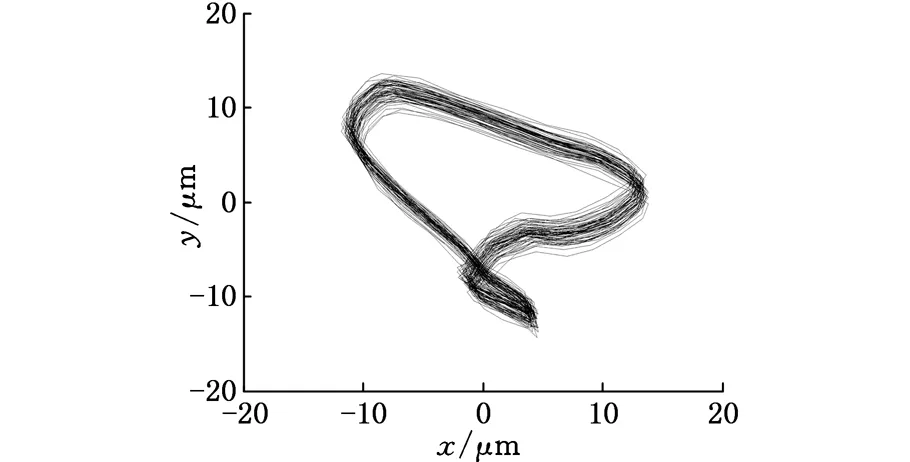
(a)测点P2处的轴心轨迹图

(b)测点P3处的轴心轨迹图图8　测点P2和P3轴心轨迹图

从图6给出的时域波形图看，测点P2有明显的M形特征，这是不对中故障的典型特征，而测点P3则看不出明显的不对中特征；图7的幅值谱图也与不对中故障的频谱特征相吻合；从轴心轨迹图看，测点P2是变形的8字形，测点P3为香蕉形，这两种轨迹均为不对中故障的典型特征，轴心轨迹形状不同，表示不对中的程度不同。因此，无论是时域波形图、幅值谱图，还是轴心轨迹图，均与新方法相吻合，证明新方法是有效的，且为不对中故障的消除提供了量化依据。

4　结论

(1)从运动学角度出发，推导了双跨转子系统联轴器动态不对中量的计算公式，通过公式能够得到平行不对中量的大小和方向以及角度不对中的大小。

(2)把本方法应用到某燃气发电机组的不对中量计算，计算结果与不对中故障的时域波形特征、频谱特征以及轴心轨迹特征相吻合，证明了本方法的有效性。

(3)本方法可以方便地推广到多转子系统的动态不对中量的计算，对于工程实际中正确对中提供了定量依据。

[1]MuszynskaA.Rotordynamics[M].NewYork:Taylor&FrancisGroup-CRCPressBook,2005.

[2]JacksonC.SuccessfulShaftHot-aligment[J].HydrocarbonProcessing, 1969, 39: 110-123.

[3]夏松波,张新江,刘占生,等.旋转机械不对中故障研究综述[J].振动·测试与诊断,1998,18(3):3-7,73.

XiaSongbo,ZhangXinjiang,LiuZhansheng,etal.ASurveyofResearchonMisalignmentofRotaryMachinery[J].JournalofVibration,Measurement&Diagnosis, 1998, 18(3): 3-7,73.

[4]陈宏，冯燕，韩捷，等.旋转机械不对中形式的新分类及其故障诊断研究[J]. 机床与液压，2010，38(7)：130-133.

ChenHong,FengYan,HanJie,etal.ANewClassificationofMisalignmentFaultofRotatingMachinesandStudyonItsDiagnosis[J].MachineTool&Hydraulics, 2010, 38(7): 130-133.

[5]韩捷.齿式联接不对中转子的故障物理特性研究[J]. 振动工程学报，1996，9(3)：297-301.

HanJie.StudyonFaultPropertiesofRotorsConnectedbytheGearCoupling[J]. 1996, 9(3): 297-301.

[6]雷文平，韩捷，李志胜，等.齿式联轴节不对中转子的动力学响应分析[J]. 机械强度，2012，34(3)：327-332.

LeiWenping,HanJie,LiZhisheng,etal.DynamicResponseAnalysisoftheRotorsConnectedbyTheMisalignedGearCoupling[J].JournalofMechanicalStrength, 2012, 34(3): 327-332.

[7]SekharAS,PrabhuBS.EffectsofCouplingMisalignmentonVibrationsofRotatingMachinery[J].JournalofSoundandVibration, 1995, 185(4): 655-671.

[8]JinWH,ChungJT.VibrationAnalysisofaFlexibleRotatingDiskwithAngularMisalignment[J].JournalofSoundandVibration, 2004, 274:821-841.

[9]BouazizS,HiliMA,MataarM,etal.DynamicBehaviourofHydrodynamicJournalBearingsInPresenceofRotorSpatialAngularMisalignment[J].MechanismandMachineTheory, 2009, 44:1548-1559.

[10]SinhaJK,LeesAW,FriswellMI.EstimatingUnbalanceandMisalignmentofaFlexibleRotatingmachinefromaSingleRun-down[J].JournalofSoundandVibration, 2004, 272: 967-989.

[11]ReddyMCS,SekharAS.DetectionandMonitoringofCouplingMisalignmentinRotorsUsingTorqueMeasurements[J].Measurement, 2015, 61:111-122.

[12]李明，李自刚. 联轴器不对中故障转子系统的动力学试验[J]. 振动·测试与诊断, 2015, 35(2)：345-351.

LiMing,LiZigang.TheoreticalandExperimentalStudyonDynamicsofRotor-bearingSystemwiththeFaultsofCouplingMisalignment[J].JournalofVibration，MeasurementandDiagnosis，2015,35(2):345-351.

[13]李凌轩，姚红良，刘子良，等. 螺纹联轴器的建模及其不对中故障研究[J]. 振动·测试与诊断，2014,34(4)：631-637.

LiLingXuan,YaoHongliang,LiuZiliang,etal.ModelingoftheThreadedCouplingandResearchonMisalignmentFailureofRotorSystem[J].JournalofVibration，MeasurementandDiagnosis，2014, 34(4):631-637.

[14]刘杨，太兴宇，姚红良，等.闻邦椿双盘转子轴承系统不对中一碰摩耦合故障分析[J].振动·测试与诊断，2013，33(5)：819-823.

LiuYang，TaiXingyu，YaoHongliang，eta1.StudyonMisalignment-rubbingCouplingFaultofDualDiskRotor：BearingSystemIncludingtheImpactofMotorCoupling[J].JournalofVibration，MeasurementandDiagnosis，2013，33(5)：819-823.

[15]LeesAW.MisalignmentinRigidlyCoupledRotors[J].JournalofVibrationandSound, 2007, 305: 261-271.

[16]XuM,MarangoniRD.VibrationAnalysisofaMotor-flexibleCoupling-rotorSystemSubjecttoMisalignmentandUnbalance,PartI:TheoreticalModelandAnalysis[J].JournalofSoundandVibration, 1994, 5: 663-679.

(编辑袁兴玲)

A Novel Quantitive Calculation Method of Dynamic Misalignment in Rotor Systems

Chen HongLei WenpingChen LeiHan Jie

Zhengzhou University,Zhengzhou,450001

The kinetic characteristics and motion forms of a twin-rotor system were analyzed from the kinetic point of view, and a novel quantitive calculation method of dynamic misalignment was proposed. The average shaft centerline positions were collected by eddy current transducers mounted on the rotor system, and translation displacements and angular displacements of shaft centerlines were calculated based on similar triangle theorem. Then according to vector synthesis principle, the amounts of the parallel misalignment and angular misalignment of the two rotors at the coupling were obtained. Engineering practices show that the calculation results are consistent with the typical features of the misalignment faults in time wave, spectrum and shaft centerline orbit. The forms and amounts of the misalignment faults might be obtained directly by this method. The novel method benefits the treatment of misalignment faults and shafting alignment in engineering practices.

misalignment; quantitive analysis; fault diagnosis; rotating machinery

2015-08-21

国家自然科学基金资助项目(51405453)

TH113

10.3969/j.issn.1004-132X.2016.17.018

陈宏，男，1976年生。郑州大学机械工程学院博士、副教授。主要研究方向为设备故障机理与智能诊断技术、机械动力学。获授权发明专利4项，发表论文70余篇。雷文平，男，1977年生。郑州大学机械工程学院副教授。陈磊，男，1979年生。郑州大学机械工程学院副教授。韩捷，男，1957年生。郑州大学机械工程学院教授、博士研究生导师。