基于L1自适应控制理论的矿井提升机调速控制器设计

罗清顺　李璟澜　刘　辉　杨秦敏

1.浙江大学，杭州,310027　2.天地科技股份有限公司，北京,100013



基于L1自适应控制理论的矿井提升机调速控制器设计

罗清顺1李璟澜1刘辉2杨秦敏1

1.浙江大学，杭州,3100272.天地科技股份有限公司，北京,100013

分析建立了整个提升机系统的动力学模型，并针对系统动态中的时变非线性、强耦合、大惯性和负荷未知等特点，设计了新的L1自适应控制器，在线学习提升机运行特性和状态，实现控制参数实时调整，获得良好的全局控制效果。数学证明表明，在自适应率足够大的情况下，L1控制器可以获得任意的稳态和瞬态跟踪精度。进而在MATLAB环境下对L1控制器进行仿真验证，并在实际的提升机物理平台上进行实验。结果表明，在载荷未知的条件下，提升机控制系统能够很好地跟踪给定的速度曲线，具有较高的控制精度和鲁棒性。

矿井提升机；未知时变动态系统；调速控制；L1自适应控制理论

0　引言

矿井提升机系统是一种具有时变、非线性和强耦合等特点的复杂不确定动态系统。同时，由于外界环境等不确定因素对工况的影响，矿井提升机的动力学参数也会随之发生变化。传统的线性PID控制算法能跟踪平滑的速度曲线，实现方法简单，但是对于被控系统中的时变和非线性特性，常规PID无法实现智能调节，无法保证全局性能，存在最优参数选取困难、动态性能差等缺点。而且，传统的调速控制器对提升系统数学模型依赖性强，无法自动调节控制参数以适应被控对象的参数变化，鲁棒性差。

针对传统控制器设计中的缺陷，李春文等[1]利用径向基函数(radialbasisfunction,RBF)神经网络(neuralnetwork,NN)辨识控制对象，把得到的雅可比矩阵信息提供给NN，再利用NN的全局逼近能力，通过自学习来实现PID控制参数的最佳组合，达到快速稳定的控制目的。该系统可实现对PID控制参数的在线调整，自适应性强、鲁棒性好，但是实现方法复杂，对辨识的准确度和在线训练方法有较强的依赖，工况变化时需要重新进行辨识学习。蔡磊[2]根据操作人员的经验编制模糊控制器的隶属度函数和控制规则。这种模糊控制器可以适用各种不同的工况，实现制动系统与调速系统的协调控制。然而，模糊控制过于依赖经验的完备可靠性，并且实现方法也较为复杂。

因此，刘淮霞[3]在原来的V-M可逆调速系统中加入前馈控制器，构成反馈加前馈的复合控制系统。它可以在不影响稳定性的前提下，彻底消灭稳态误差，实现S形速度给定曲线的准确跟踪。但是，这种方法对于参数的时变性和各种干扰并没有给出针对性的措施。田艳兵等[4]采用先进的H∞鲁棒控制理论，把控制问题归结为混合灵敏度问题，求取闭环系统传递函数阵最大奇异值，较好地解决了外部干扰和系统摄动的影响，具有较强的鲁棒性。另外，还有学者提出其他调速控制算法，如蚁群算法[5]、改进粒子群细菌觅食算法[6]等，可对PID控制器参数进行优化；迭代学习控制算法[7]可利用矿井作业的重复运行特性提高提升机的跟踪性能；混沌优化算法[8]可用于设计模糊PID控制器等。然而，这些方法由于计算量过大等因素的影响，实用性受到局限，无法很好地保证变化工况下的控制性能。

另一方面，模型参考自适应控制器(modelreferenceadaptivecontrol,MRAC)非常适用于时变、强耦合的非线性不确定动态系统，通过反馈的系统状态信息进行在线学习，使控制器可以根据提升机系统特性的变化实现控制参数在线实时调整，从而在整个非线性工作区间内保证良好的全局控制效果[9]。L1自适应控制器作为一种改进的MRAC，在设计的自适应率足够大的情况下，可以获得非常高的跟踪精度。在实际被控系统与表征理想性能的参考模型出现差别时，依然能够给出相应的补偿规则，使被控系统具有与理想模型相似的动态特性，从而维持所期望的运行动态性能[10]。

1　提升机运动控制系统动力学分析

1.1提升机运行速度曲线的特点

1.1.1提升机速度的周期性

提升机的运行速度曲线通常如图1所示，实行周期性运转，在t0时刻前为初加速阶段，为了减小对井架的冲击，初加速度较小；t0～t1时刻为主加速阶段，为缩短起动时间，箕斗运行出卸载曲轨后提升至最大速度vm；t1～t2时刻为等速阶段，此时箕斗以恒定的速度vm在井筒中运行；t2～t3时刻为减速阶段，此时箕斗已经接近井口或装载点，应减速至期望的速度v4；为减小冲击，t3～t4时刻则以爬行速度v4缓慢爬行；到达终点后，提升机停止运转。

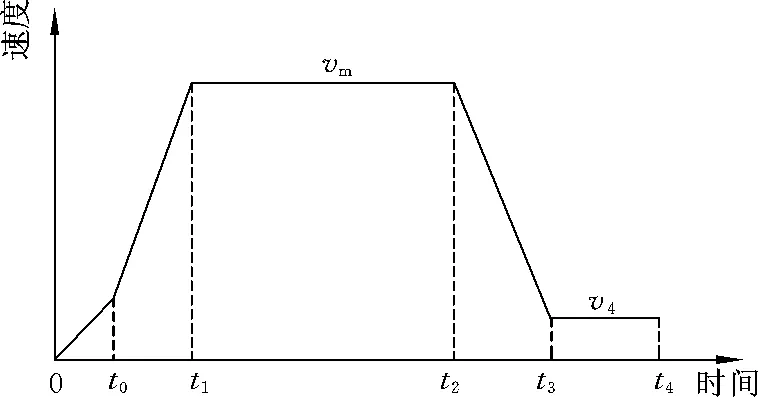
图1　典型的提升机运行五段速度图

1.1.2电动机的两种工作状态

根据运行目标的不同，电动机有两种工作状态。当电动机轴上受的力矩方向与箕斗的运动方向相反(如提升重物)时，需要电动机发出拖动转矩(即电动状态)，称之为正力；当轴上受力方向与箕斗运动方向相同(如下放重物)时，为了限制下放重物的速度，可采用制动状态，称之为负力。

1.1.3加速度、减速度的限制

由于提升系统存在弹性环节(绳索)，实际情况中还存在着减速器的齿轮间隙等因素造成的非线性特性，加速度过大时，会产生过大的机械动应力，加速机械疲劳，缩短提升机寿命。因此，在控制器的设计上，不仅仅需要衡量稳态性能，还要充分考虑瞬态跟踪性能。

1.2提升机调速系统数学模型的建立

控制器和执行机构之间的数学关系是进行理论分析和具体控制器设计的重要依据，所以需要首先完成提升机系统数学模型的建立，推导出系统的动力学方程。提升机的运行包括上提和下放重物两个方向的运动，天轮主要起导向作用，如图2、图3所示。考虑到重物的质量通常比天轮高几个数量级，可以将天轮的重量略去，并把整个提升系统的相应物理量都变位到卷筒上来进行动力学分析。

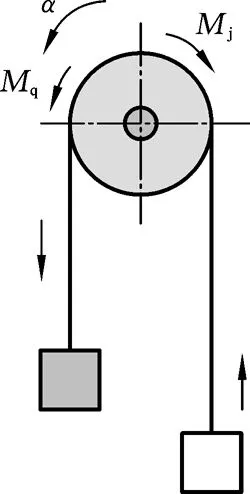
图2　　　　下放重物受力　　　示意图

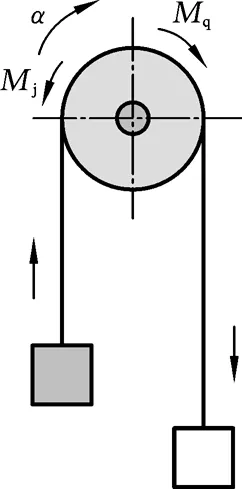
图3　　　　上提重物受力　　　示意图

为了简化分析过程，将矿井提升机各个部件的转动惯量都换算到半径为R的卷筒圆周上，得到变位质量。整个系统的转动惯量J与变位质量之间的数学关系如下：

J=∑mR2

(1)

式中,∑m为提升系统各部件换算到卷筒圆周上的变位质量，kg；R为钢丝绳的缠绕半径或卷筒半径，m。

当提升机在运行时，按照图2、图3所指示的物理量正方向和牛顿定律可得

(2)

式中,Mq为电机产生的驱动力矩，作为控制输入量，如前所述，可为主动力矩或者制动力矩，N·m；Mj为静阻力力矩，N·m；α为卷筒的转动角加速度，rad/s2；ω为卷筒的转动角速度，rad/s。

1.2.1提升系统的变位质量

变位质量的引入是为了将不固连在一起的各运动部件的质量都换算到半径为R的卷筒圆周上，使其角速度和角加速度与卷筒圆周上的值相等，从而获得更简便的计算表达式。变位折算的前提是变位前后的动能必须相等。

在实际应用中，由于各运动部件的状态不同，整个系统的变位质量是一个有着微小变化的量。由于大负荷的存在，这种微小变化可以忽略不计。因此，本文中采用理论计算的方法得到的竖井提升系统变位质量是一个定值，理论计算的公式如下：

(3)

式中，g为重力加速度；Q为载荷，N；QZ为提升容器自重，N；n1为首绳根数；p为首绳每米重，N/m；Lp为首绳悬挂长度，m；n2为尾绳根数；q为尾绳每米重，N/m；Lq为尾绳悬挂长度，m；Gi为天轮的变位重力，N；Gj为卷筒的变位重力，N；Gd为电机转子的变位重力，N。

1.2.2提升系统的静阻力矩

提升系统的静阻力矩实际上由多个力矩组成。为了方便研究，将它们的作用效果都折算到半径为R的卷筒圆周上。不考虑重载，只考虑上升端和下降端悬挂钢丝绳以及提升容器(罐笼或箕斗)对卷筒产生的静阻力，见图4。其中，静阻力矩的计算公式为

Mj=FjR

(4)

其中，Fj为提升系统除去电机产生的主动力或制动力外提升系统的静阻力。提升系统的静阻力表达式为

Fj=Fqz±Gh

(5)

式中，Fqz为荷载和摩擦力产生的静阻力；Gh为钢丝绳对卷筒的静阻力；计算符“+”、“-”分别表示上提重物、下放重物。

考虑到首绳和尾绳对提升机卷筒静阻力的合

图4　上升过程钢丝绳和提升容器产生的静阻力

力为Gh=Gs-Gx，可得

Gh=Δs(HD-hx)-Δxhx

(6)

式中，Gs为上升端钢丝绳和容器对卷筒的静阻力；Gx为下降端钢丝绳和容器对卷筒的静阻力；Δs为首绳和尾绳每米自重，N/m；HD为井深，m；hx为某时刻提升容器所在位置高度，m；Δx为下降端钢丝绳每米自重，N/m。

分析了钢丝绳对卷筒的静阻力，还需考虑载荷Q对卷筒的静阻力。同时，系统内部还存在着摩擦阻力，如轴和轴承之间、容器和导向轨道之间等。这些阻力在提升过程中也会随时发生变化，很难精确计算。通过实验可以测出它们的合力作用与提升重载的自重近似成线性关系，即

Fqz=KQ

(7)

式中,K为矿井阻尼系数。

将式(6)和式(7)代入式(5)，可得

Fj=KQ±[Δs(HD-hx)-Δxhx]

(8)

由式(4)和式(8)可以得出系统的静阻力距：

Mj={KQ±[Δs(HD-hx)-Δxhx]}R

(9)

由式(9)可得，只要测得系统在任意时刻的提升高度和载荷，即可以确定提升系统的静阻力矩。然而，这种计算方法本身存在着数学近似，并且由于很多参数不可精确测量(如矿井阻尼系数K)，或者会随时间变化(如载荷Q)，系统模型中存在大量的不确定性，传统的控制参数固定的控制器设计必然无法得到全局优化的控制效果。因此，面向提升机系统，本文提出一种新的具有学习能力的L1自适应控制器，以获得鲁棒的跟踪性能。

2　L1自适应控制器设计

首先，对建立的理想模型(式(2))进行变换，可得

(10)

如果该模型中的参数都精确可测，简单的线性控制或最优控制就能获得满意的闭环控制效果。然而，该理想模型是由理想情况下的物理定律得到的，与实际系统的动力学特性有一定的误差。同时，系统模型是关于状态变量ω的非线性函数，具体的表达式无法精确给出[11]。而且，现有的矿井提升机控制系统并没有充分考虑到在提升机工作时，转动惯量J也会发生变化，转动惯量与矿井提升机的转动角速度ω及当前位置有关。因此，本文的目标是在系统模型具体参数未知和具有时变特性的前提下，通过设计一种自适应控制率调节控制信号Mq，使提升机的实际角速度输出ω跟踪给定的理想速度曲线，并在加速、减速和匀速等各阶段都获得较好的稳态和瞬态跟踪性能。

充分考虑上述的不确定性以及参数的不准确等因素，实际模型(式(10))可重新表示为

(11)

式中,u(t)为驱动力矩控制输入，即Mq；Am和b为自主设计的控制参数；φ(t)为驱动力矩输出增益的变化，代表未知控制增益的时变性；Amω(t)+bθ(t)ω(t)为与转动角速度ω相关的转矩项；θ(t)为ω变化引起的转矩时变特性；σ(t)为由参数时变和外部干扰等引起的实际模型与参考模型之间的可匹配误差。

参考模型在一定程度上可以根据期望的动态特性对应的零极点位置来设计，但要受到规定的参考模型理想性态应当是被控对象可以达到的这一物理要求限制。基于实际模型可以简化得到提升机的低阶线性参考模型。

在给出L1自适应控制率之前，首先给出状态预测器，对提升机速度进行在线估计:

(12)

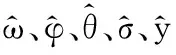
实际的提升机速度能够维持在给定速度曲线附近，允许在很小范围内变化。以此作为目标，可以推导得到参考模型的转矩调速控制律。实际的提升机模型与低阶线性的参考模型之间会存在差别。进一步构造控制器中的可校正参数表征系统可变参数对输出的作用，采用自适应机制在线调整可校正参数可以抑制系统参数变化和扰动带来的性能不稳定。

因此，进一步构造控制器中的可校正参数表征系统可变参数对输出的作用，得到实际控制率：

(13)

kg=-Amb-1, k>0

式中，χ(t)为控制率中引进的中间变量。

在这里，控制器中加入了低通滤波器环节。低通滤波器以频域形式可以表示为a/(S+k)，用于消除电机转矩控制量中的高频分量，降低调节器的调整频率，从而延长电机的使用寿命。进而，为控制器设计自适应机制实现在线调整可校正参数，对系统参数变化和时变特性带来的性能不稳定进行补偿:

(14)

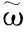
因此，整个提升机L1自适应控制系统由状态预测器(式(12))、基本自适应控制器(式(13))和自适应机制(式(14))三部分组成，如图5所示，其中ωref为参考转动角速度。

图5　L1提升机调速控制器框架

由于篇幅原因，稳定性证明请参考文献[10]。

定理1表明，通过采用L1自适应控制系统，可以实现实际被控对象对参考模型的跟踪信号一致收敛，即使被控对象的参数不确定，相应的控制律仍然可以使系统的实际速度输出一致逼近理想参考模型的输出。而且，收敛的结论对稳态和瞬态输出都是成立的。也就是说，在瞬态过程中，系统的实际输出也能一致逼近期望的理想曲线，从而获得更好的控制效果。考虑到转矩作为控制量可以实现短时间的快速调节，在适当加大自适应增益的情况下，控制精度能够得到很好的提升，这也是L1用于提升机系统的优势。

同时，状态预测器的存在可以对系统运行状态和特性变化做在线学习，对于提升机这种存在多扰动、载荷未知的系统有很好的自适应调整能力。提升机本身作为大惯性系统，通过设计合理的状态预测器中参考模型参数可以合理地表征提升机的动态特性，提高在线学习的准确度。

3　仿真结果

在本节中，使用仿真软件MATLAB验证我们设计的L1自适应控制器的性能。在仿真过程中所用的提升机系统参数设置如下：钢丝绳的缠绕半径R=1m;重力加速度g=9.8m/s2;载荷Q=10 000N;提升容器自重QZ=5900N;首绳根数n1=4;首绳每米重Fp=20N/m;首绳悬挂长度Lp=445m;尾绳根数n2=2;尾绳每米重Fq=20N/m;尾绳悬挂长度Lq=400m;天轮的变位重量Gi=307kg;卷筒的变位重量Gj=11 010kg;电机转子的变位重量Gd=7273kg;最大提升速度vm=8m/s;井深HD=424m;首绳和尾绳每米自重Δs和下降端钢丝绳每米自重Δx都为20N/m;箕斗提升时矿井阻尼系数K=1.15，罐笼提升时K=1.2。

(15)

其中，Am=-350，b= 0.02，uipart(t)=-kgr(t)。

对控制器中的学习率参数进行设置，设计控制器自适应率中参数取值为Γθ=140 000 000，Γσ=90 000 ，Γφ=10，P=1，k=1。仿真时采用的采样周期和控制周期皆为0.001s。

为了更好地验证所设计控制算法的有效性，我们对提升机在上升阶段中不同载荷条件下进行了大量的仿真实验。

3.1载荷为104N时的实验结果

当载荷为104N时，提升机的速度输出如图6所示，能够很好地跟踪理想的速度曲线。而且，动态过程比较平滑，完全能满足矿井提升机的动态响应要求。同时，电机的转矩输出(即控制信号)也显示于图7，表示控制信号的有界性。

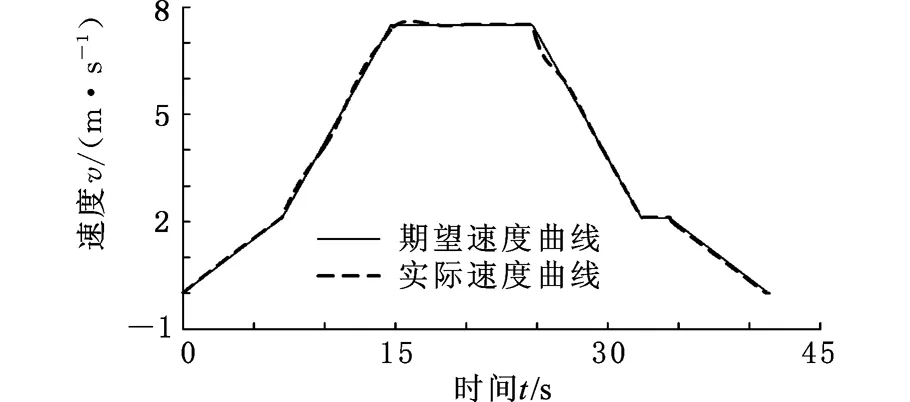
图6　载荷为104 N时的速度曲线

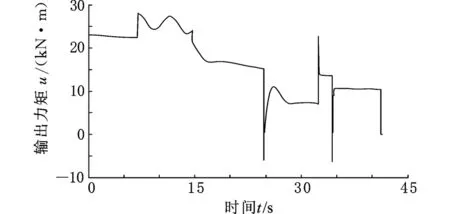
图7　载荷为104N时的电动机输出力矩曲线

3.2载荷为1.5×104N时的实验结果

当载荷变为1.5×104N时，在不改变控制器任何参数的前提下，提升机的速度输出如图8所示。虽然由于负荷的增加，在前期的速度跟踪上出现了一定的误差，但可以发现，本文提出的控制算法不需要对系统参数重新估计，也不需要对控制器重新设计，依然能够很好地使系统输出跟踪理想的速度曲线。同时，电机的转矩输出(即控制信号)也由图9给出，以显示控制信号的有界性。

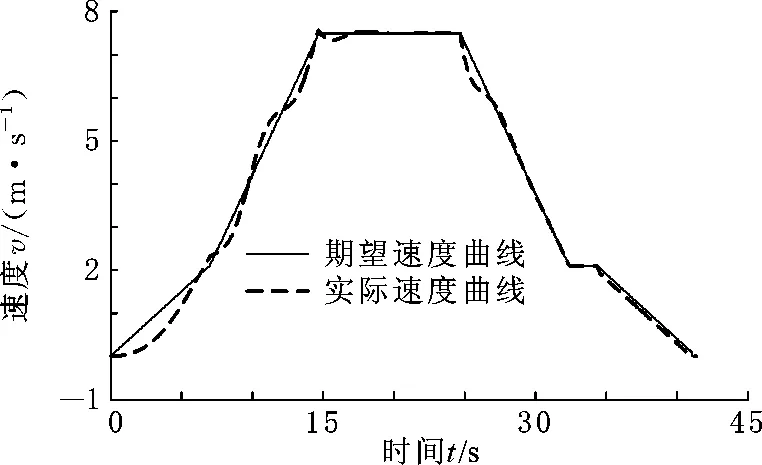
图8　载荷为1.5×104 N时的速度曲线

综合仿真结果表明，当载荷变化时，控制器完全不需要改变自身的参数设置，就可以较好地跟踪给定的速度曲线，保证主加速过程和减速过程提升机的平稳运行。因此，整个控制器具有较强的鲁棒性，可以方便地应用于不同的提升机系统。

图9　载荷为1.5×104 N时的电动机输出力矩曲线

4　实际应用

在仿真实验的基础上，将L1提升机调速控制器进行改进优化设计后应用于峰峰集团某煤矿副井提升，该矿提升系统采用JKMD-5.5×4(Ⅲ)E型落地4绳摩擦式矿井提升机，配有2700kW、38.2r/min交流变频同步电动机，电机与提升机直联，提升系统最大提升速度为11.0m/s。图10～图13为现场几种工况的实际运行曲线，图中曲线1为提升机设定速度，曲线2为提升机实际速度，曲线3为设定力矩输入。运行结果表明基于L1自适应控制理论的调速控制器调速平稳，效果良好。

4.1半载提升运行工况

此工况中，罐笼1重13.5t，罐笼2处于空载状态，提升机运行方向为罐笼1上提，提升速度为11m/s，加速度为0.7m/s2，减速度为0.75m/s2，系统超调量取0.5%。该工况下运行曲线见图10。

图10　半载提升运行曲线图

4.2半载下放运行工况

此工况中，罐笼1重13.5t，罐笼2处于空载状态，提升机运行方向为罐笼1下放，提升速度为11m/s，加速度为0.7m/s2，减速度为0.75m/s2，系统超调量取0.5%。该工况下运行曲线见图11。

4.3满载半速提升运行工况

此工况中，罐笼1重27t，罐笼2重13.5t，提升机运行方向为罐笼1上提，提升速度为6m/s，加速度为0.7m/s2，减速度为0.75m/s2，系统超调量取1.5%。该工况下运行曲线见图12。

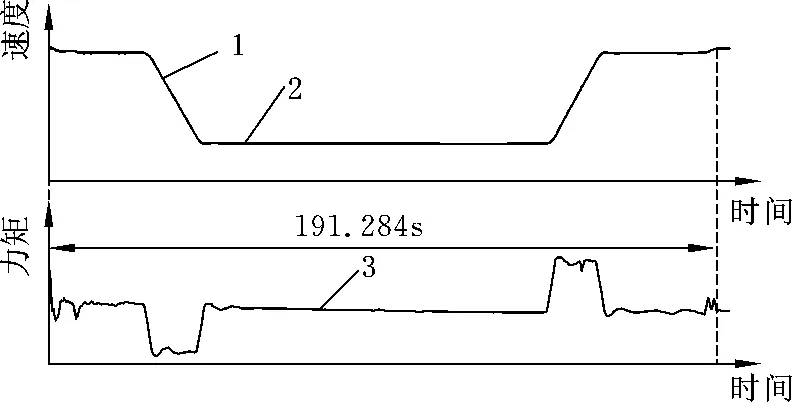
图11　半载下放运行曲线图

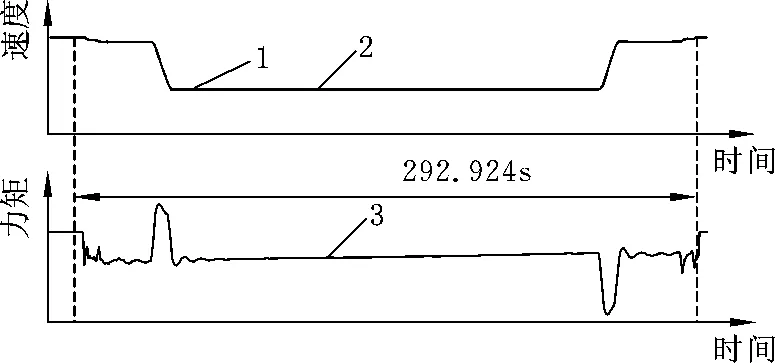
图12　满载半速提升运行曲线图

4.4满载半速下放运行工况

此工况中，罐笼1重27t，罐笼2重13.5t，提升机运行方向为罐笼1下放，提升速度为6m/s，加速度为0.7m/s2，减速度为0.75m/s2，系统超调量取1.5%。该工况下运行曲线见图13。

图13　满载半速下放运行曲线图

5　结语

本文采用实际的提升机物理参数在MATLAB环境下对L1控制器进行了仿真，证明在载荷变化时，提升机系统依然能够很好地跟踪给定的速度曲线，这表明该系统具有较高的控制精度和鲁棒性。同时，本文设计了相应的控制算法并在实际被控系统上进行测试，实验结果表明采用的控制策略能够维持其所期望的提升机运行状态。与PID控制器相比，L1控制器运行过程中的参数自适应调整使得其不需要重新进行参数整定或设置即可保证良好的控制效果，该特性使得其在某些由于系统特性发生变化而需要重新设置控制参数的场景中具有较强的应用价值。

[1]李春文,曹玲芝,张爱芳,等.神经网络PID控制器在提升机控制系统中的应用[C]//第29届中国控制会议论文集.北京,2010:71-74.

[2]蔡磊.模糊控制在矿井提升机调速系统中的应用[D]. 阜新:辽宁工程技术大学,2009.

[3]刘淮霞.矿井提升机复合控制系统的仿真分析[J].安徽理工大学学报(自然科学版), 2011, 31(4): 22-24.

LiuHuaixia.SimulationAnalysisofMineHoistCompoundControlSystem[J].JournalofAnhuiUniversityofScience&Technology(NaturalScience), 2011, 31(4): 22-24.

[4]田艳兵,卢燕.H∞控制理论在直流矿井提升机调速系统中的应用[J]. 煤矿机械, 2010, 31(3): 194-196.

TianYanbing,LuYan.ApplianceofH∞TheoryinSpeedControlSysteminDCMineHoist[J].CoalMineMachinery, 2010, 31(3): 194-196.

[5]杨柳,刘建国. 基于改进粒子群细菌觅食算法的矿井控制研究[J]. 计算机测量与控制, 2014, 22(1): 113-115.YangLiu,LiuJianguo.BasedonImprovedParticleSwarmForagingBacteriaMineControlResearch[J].ComputerMeasurement&Control, 2014,22(1): 113-115.

[6]余发山,岳伟超,张瑞庄,等.基于迭代学习的矿井提升系统跟踪控制[J]. 电子测量与仪器学报, 2014, 28(2): 138-145.YuFashan,YueWeichao,ZhangRuizhuang,etal.MineHoistSystemTrackingControlBasedonIterativeLearning[J].JournalofElectronicMeasurement&Instrumentation, 2014, 28(2): 138-145.

[7]郝晓弘,胡振邦,郝守庆,等. 模糊PID迭代学习控制算法在矿井提升机中的应用[J]. 工业仪表与自动化装置, 2011(1):6-8.HaoXiaohong,HuZhenbang,HaoShouqing,etal.ApplicationofFuzzyPIDILCinMineHoist[J].IndustrialInstrumentation&Automation, 2011(1):6-8.

[8]林金泉. 基于混沌优化的矿井提升机的控制仿真研究[J]. 电气应用,2012(8):28-31.

LinJinquan.ControlSimulationStudyofMineHoistBasedonChaosOptimization[J].ElectricControl,2012(8):28-31.

[9]DattaA,IoannouPA.PerformanceAnalysisandImprovementinModelReferenceAdaptiveControl[J].IEEETransactionsonAutomaticControl, 1994, 39(12): 2370-2387.

[10]HovakimyanN,CaoC.L1AdaptiveControlTheory:GuaranteedRobustnesswithFastAdaptation[M].Philadelphia:SocietyforIndustrial&AppliedMathematics, 2010.

[11]李启龙. 矿井提升机直流调速系统自适应控制的研究[D]. 青岛：山东科技大学, 2007.

(编辑王旻玥)

MineHoistSpeedControllerDesignBasedonL1AdaptiveControlTheory

LuoQingshun1LiJinglan1LiuHui2YangQinmin1

1.ZhejiangUniversity,Hangzhou, 310027 2.TiandiScience&TechnologyCo.,Ltd.,Beijing, 100013

Aminehoistsystemdynamicmodelwasfirstlyanalyzed.Accordingtothecharacteristicsoftime-variation,nonlinearity,strongcoupling,greatinertia,unknownloadwithinthesystemdynamics,anewL1adaptivecontrollerwasadoptedtoonlinelearntheoperatingconditions,toadjustthecontrollerparametersinrealtime,andwellcontroleffectivenessintheglobalenvironmentwasobtained.L1controllerwasprovedtohavearbitrarysteadystatesandtransienttrackingprecisionwhentheadaptivegainwaschosenlargeenoughthroughstrictmathematicalverification.ThenthefeasibilityofL1controllerwasvalidatedinMATLABsimulationenvironmentandatestwasconductedinrealmechanicalplatform.Theresultsshowthattheminehoistcontrolsystemmaystilltrackthegivenspeedcurvealongwithsatisfactorytrackingaccuracyandrobustnesswhentheloadisunknown.

minehoist;unknowntime-varyingdynamicsystem;speedcontrol;L1adaptivecontroltheory

2014-11-24

国家高技术研究发展计划(863计划)资助项目(2012AA06A404)

TD63

10.3969/j.issn.1004-132X.2016.17.010

罗清顺，男，1991年生。浙江大学控制科学与工程学院硕士研究生。主要研究方向为自适应控制理论。李璟澜，男，1993年生。浙江大学控制科学与工程学院博士研究生。刘辉，男，1978年生。天地科技股份有限公司储装系统事业部工程师。杨秦敏，男，1979年生。浙江大学控制科学与工程学院副教授、博士研究生导师。