基于车−桥耦合振动理论的连续梁桥影响因素分析
张向东,杜东宁,柴源,刘佳琦
基于车−桥耦合振动理论的连续梁桥影响因素分析
张向东,杜东宁,柴源,刘佳琦
(辽宁工程技术大学土木与交通学院,辽宁阜新,123000)
通过研究车辆模型及桥梁模型,基于接触点位移协调条件,建立车−桥系统耦合振动运动方程组。用有限元软件MIDAS/CIVIL分析不同影响因素下桥梁的动力特性,揭示桥梁跨中竖向位移、弯矩冲击系数、竖向加速度等指标的变化规律。根据有限元分析结果,编译车−桥耦合振动系统影响因素分析程序,研究各因素对桥梁动力特性的影响。研究结果表明:车辆速度、行车数和桥面不平整度都对桥梁的动力特性有一定程度的影响;车辆速度对跨中竖向位移的影响最大,桥面不平度对跨中竖向加速度的影响最大,跨中弯矩冲击系数受车辆速度的影响最大。最后通过正交试验验证该程序分析结果的可靠性。
车−桥耦合;动力性能;影响因素;有限元软件
随着我国经济的发展,车流密度的不断加大,桥梁数量日益增多。为研究桥梁工作状态和安全性等问题,研究人员将移动荷载作用下的桥梁振动方程发展成车−桥耦合振动系统[1]。近年来,各国学者对车−桥系统耦合共振问题做了很多研究。郗艳红等[2]把车辆简化为移动质点,指出了桥梁质量移动速度与动力系数的关系。李永乐等[3]将桥梁化为等长的欧拉梁,研究了桥面不平度、桥梁损伤、汽车参数等因素对桥梁动力特性的影响。AUFTK等[4]用数据统计的方法得出了轴重的分布规律,并用模拟随机车流的方法分析了车−桥系统振动问题。韩万水等[5]则将车−桥耦合系统发展为可以将随机车流考虑在内的新型分析系统。而将外界附加因素考虑在内的车−桥耦合系统问题也受到各国学者关注。LADISLAV等[6]研究了风−车−桥三因素耦合作用下桥梁振动问题。YANG等[7]在有限元框架内对震动激励下的车−桥耦合系统进行了稳定性分析。李忠献等[8]建立了考虑结构相互作用的三维空间模型,分析了地震作用对车−桥耦合系统的影响。谭长健等[9]采用实测的路面粗糙度样本分析了路面粗糙度对车−桥耦合振动系统的影响,并得到路面粗糙度的相关性对车辆响应有重要影响的结论。分析已有的文献可以发现研究成果大致分为2类:一类主要是将车−桥耦合系统发展成为更完整、更全面的计算模型,另一类则是尽量考虑多因素耦合作用下的车−桥系统的力学性能与安全性能方向的研究。而研究各种因素对车−桥耦合系统的影响程度的却为数不多。因此,本文作者在参阅相关参考文献的基础上建立车−桥耦合系统振动模型,以有限元软件MIDAS/CIVIL为平台,综合考虑车−桥受力状态以及车辆速度、行车数、桥面不平整度等因素的影响,分析了桥梁的动力特性并编写用于分析各因素对车−桥耦合系统影响程度的专业程序DCBA。并通过自编程序分析了各个因素之间影响程度的主次关系,为实际工程应用提供了便利的条件和有力的帮助。
1 车−桥−耦合振动模型的建立
1.1 1/2车辆模型的建立
常见的车辆模型可简化成为一个具有4个自由度的运动系统[9−11],如图1所示。

图1 1/2车辆模型
该系统由 1 个主车体、2 幅转向架、2个轮对组成,并由弹簧和阻尼器将这几部分结合到一起。其中悬挂装置联接转向架与车体,车身质量为s,并将车辆的前轴设为质量t1、后轴设为质量t2且具有弹性阻尼系统的运动刚体,其对应的弹性系数分别为s1和s2,黏滞性阻尼系数分别为s1和s2。前、后车轮轮胎的弹性系数分别为t1和t2,各轮的阻尼系数分别为t1和t2。此时,若设定静力平衡位置为坐标原点,车体的竖向为位移3和4(通过车体质心的竖向位移s与水平转角之间的关系可计算得出),2幅车架的竖向位移分别为t1和t2,车体距车轮的质心距离分别为1和2,车轮与桥梁接触点的竖向位移为c1和c2。则有

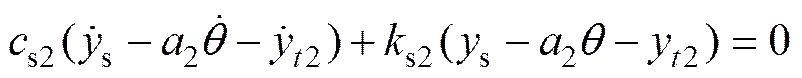






将上式改写为矩阵形式为

式中:v,v和v分别为车辆模型的质量、阻尼、刚度矩阵;v为位移向量;v为桥面接触点与车辆胎之间的瞬时耦合荷载向量;v为重力荷载向量。
1.2 桥梁子系统的动力学模型
研究桥梁与车辆的耦合振动问题时,一般将桥梁视为空间有限元模型,并设其质量、刚度和阻尼特性沿桥跨方向均匀分布,则有其振动方程为

式中:t,t和t分别为桥梁模型的质量、阻尼、刚度矩阵;t为位移自由向量;t为作用外力向量。
1.3 车−桥耦合模型运动方程的建立
从虚功原理出发,并结合大质量法[12]来考虑车−桥之间的耦合作用,联系1/2车辆模型和桥梁子系统的动力学方程,可得车−桥耦合作用的模型,如图2所示。此时,车−桥耦合振动系统简化为车体、支悬系统、车轴和轮胎几个组成部分。当车辆模型采用1/2模型时,车辆与桥面的接触点有2个。根据作用力与反作用力的关系可知,行驶于桥面的车辆,其车轮在桥面的激励作用下,相当于形成一个作用于车轮的反力,车−桥系统通过车辆与桥梁之间的接触点位移协调条件[13]相连接,从而完成了2个模型之间的力学条件耦合,其运动方程可表示为

式中:,和分别为车桥耦合振动模型的质量、阻尼和刚度矩阵;为位移向量;为作用外力向量。

图2 车−桥耦合作用模型
2 车−桥耦合振动模拟分析
所建立模型参照的实际工程为阜新市绕城公路工程。建立尺寸为(63.6 m+85 m+63.6 m)预应力混凝土连续梁桥模型。桥梁共27 m宽,单幅桥面宽度为13 m,双向六车道。主梁横断面按单室单箱箱型截面设计,箱梁顶板宽度12 m,底板宽度6 m,支点处箱梁高5.2 m,跨中处高2.8 m,底板按2次抛物线变化,腹板宽度按直线变化。为满足桥面横向布置和减轻自重,箱梁顶面翼缘板设置成2%向外侧的单面横坡。各跨的跨中和边跨现浇梁段梁高均为2.8 m。箱梁外侧腹板采用直腹板,厚度由箱梁梁体根部60 cm渐变至跨中直线段35 cm处,顶板厚30 cm。桥墩采用瓶式墩,基础为钢筋混凝土扩大基础。箱梁采用C50混凝土,桥墩采用C40混凝土。
通过MIDAS/CIVIL 建立有限元模型,车−桥耦合振动模型采用式(7)。设计荷载为公路Ⅰ级,结构按承载能力极限状态设计,全桥共117个节点,104单元,1/2车辆模型截面的抗弯惯性矩为b=144=144×103mm4,车辆模型前、后轴质量分别为1=2=36 000 kg。其钢筋结构与混凝土结构的力学参数均采用MIDAS/CIVIL内置默认值。所建立的桥梁有限元模型如图3所示。

图3 桥有限元模型
根据刘波等[14]的研究,影响车−桥耦合系统振动作用的主要因素包括车辆行驶速度、车体质量、行车数、桥面平整度、桥梁损伤5个方面。本文重点分析车辆速度、行车数和桥面平整度3个因素。由于桥梁每跨的1/2跨中处弯矩最大,桥梁的最不利荷载位置大多集中在该截面,故本文的动力性能研究主要针对该桥的首跨、中跨和尾跨的3个跨中截面。在动力性能参数选取方面,根据刘献栋等[15]的相关研究,选取跨中竖向位移、跨中弯矩冲击系数以及行车过程中的跨中竖向加速度为主要分析对象。
为了方便分析,当对某一影响因素进行研究时,其他参数固定为代表值,以此来考虑各个因素单独变化时对车−桥耦合系统的影响规律。各研究对象所对应的分析范围与代表值见表1。

表1 各指标参数
3 模拟结果分析比较
3.1 车速对车−桥耦合振动的影响
考虑车速从30~120 km/h的不同变化,通过分析计算得出不同车速下代表点处的跨中竖向位移、弯矩冲击系数、竖向加速度,结果如图4所示。因为图4(b)和(c)中曲线无明显规律性,故加入平均值变化量,以便于分析比较,而图4(a)中变化规律基本呈线性趋势,故没有加入平均值变化量。由图4可以看出:当车速发生变化时,跨中竖向位移随车速呈线性变化,车速的增加对竖向位移的影响很大,且对中跨的影响效果最明显。而跨中弯矩冲击系数随车速变化规律曲线基本不存在单调性,数值相对比较离散,整体变化趋势比较平缓,其中最大值出现在尾跨,此时时速为120 km/h。对于竖向加速度随车速变化的规律曲线,当车速增加时,跨中竖向加速度出现不规则上升变化。观察图4(c)与图4(a)中的曲线梯度可知:在车速从30~120 km/h的变化过程中,竖向位移变化增幅为128.4% ,竖向加速度增幅为114.3%。可见车速对跨中竖向加速的影响更大一些。
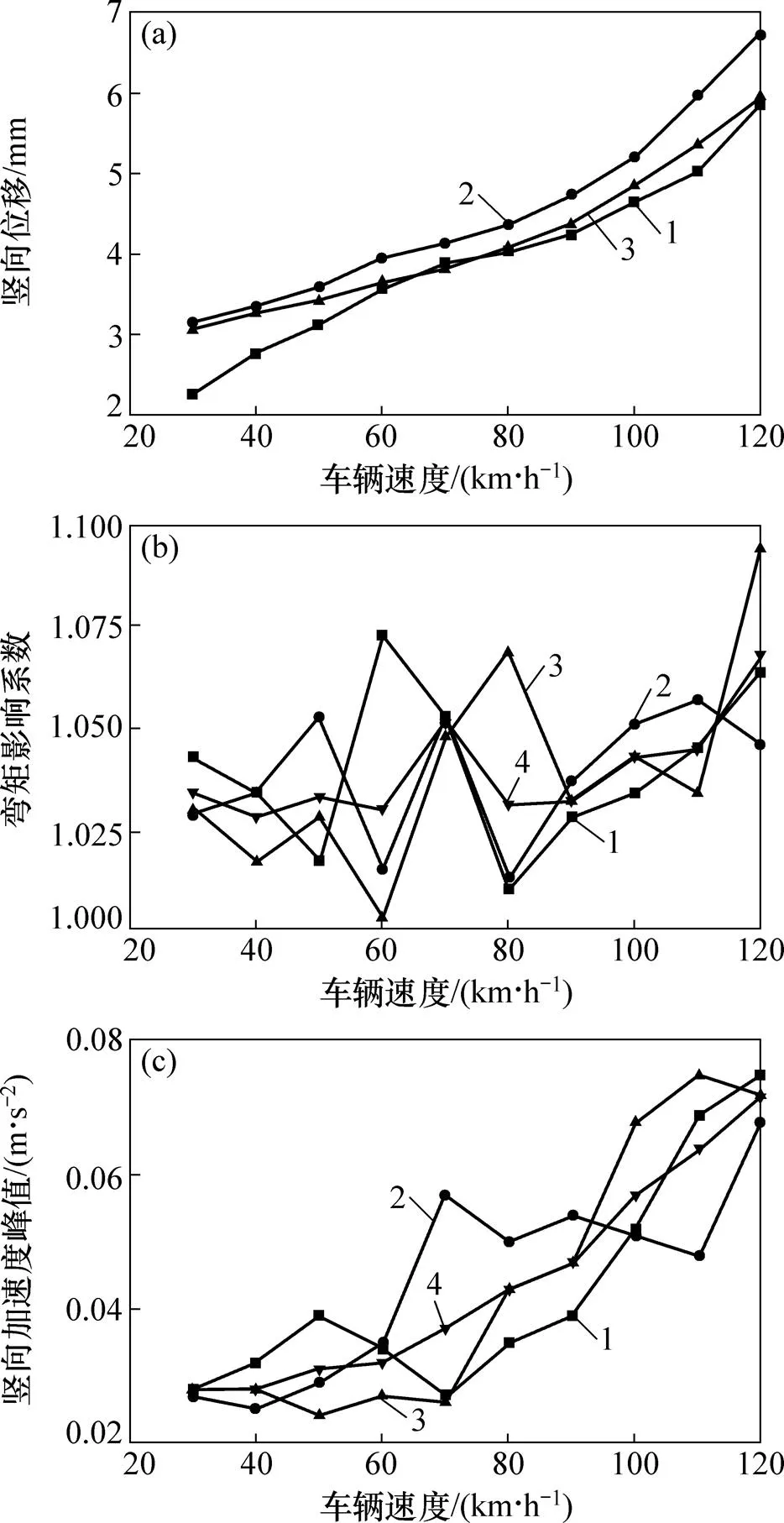
(a) 竖向位移;(b) 弯矩冲击系数;(c) 竖向加速度
1—首跨;2—中跨;3—尾跨;4—平均值。
图4 车辆速度对跨中的影响
Fig. 4 Effects of vehicle speed on vertical displacement at mid-span
3.2 行车数对车−桥耦合振动的影响
将行驶车辆数量设定在1~10之间变化(步长为1),运用MIADS/CIVIL模拟各个不同状态下车−桥耦合系统内各代表点的变化规律,结果如图5所示。由图5可以看出:当桥面车辆行驶数发生变化时,跨中竖向位移、弯矩影响系数、竖向加速度的数值变化都无明显规律,曲线不存在线性单调性。其中跨中竖向位移随着车辆的增加呈轻微上升趋势,弯矩与加速度则变化平缓,没有表现出明显的增减趋势。

(a) 竖向位移;(b) 弯矩冲击系数;(c) 竖向加速度
1—首跨;2—中跨;3—尾跨;4—平均值。
图5 车辆数对跨中的影响
Fig. 5 Effects of vehicle number on vertical displacement at mid-span
另外,无论在哪一种影响因素的作用下,中跨代表点的变化曲线基本都在平均值以上。说明行车数的变化对中跨的影响最大,其出现峰值时行车数一般在8~10之间。
3.3 桥面不平整度对车−桥耦合振动的影响
路面不平整度是指路表面相对于基准面的偏离程度。大量的试验测量表明,路面不平整度是具有零均值、各态历经的平稳Gauss随机过程[15]。在实际工程中,通常用有一定频率的功率频谱来模拟路面的不平整度,该功率频谱可拟合为

式中:x()为位移功率谱密度;x(0)为路面不平整度系数;为空间频率,m−1;0为空间参考频率,0=0.1(−1);为频率指数,一般取=2。
按照功率谱密度,公路路面一般可分为8个等级,在中国高等级公路基本属于A,B和C这3个等级,桥面不平整度也可参照这3个等级进行设定。运用有限元分析软件,模拟各个路面等级下车−桥耦合振动系统对桥梁动力特性的影响规律,结果如图6所示。由图6可以看出:当桥面平整度发生变化时,变化规律曲线都呈上升趋势,每当公路等级降低一级时,其增幅程度约为50%,且公路等级越低,其各项数值越大。可见路面平整度对车−桥耦合振动的影响不容忽视,分析中应予以考虑。

(a) 竖向位移;(b) 弯矩冲击系数;(c) 竖向加速度
1—首跨;2—中跨;3—尾跨。
图6 桥面平整度对跨中竖向加速度的影响
Fig. 6 Effects of pavement evenness on vertical displacement at mid-span
4 影响因素分析程序
4.1 程序简介
观察模拟计算结果,可以看出车辆速度,行车数和桥面不平整度都对桥梁的动力特性有一定程度的影响。但是只观察图4~6难以分辨哪个因素影响程度最大。以往研究各个影响参数对某一事物的影响程度时,常用正交试验法进行分析。但当影响因素或水平因素过多时,需要进行大量正交试验和繁琐的分析才可得出有效的结果。为简化计算步骤和节约时间,特开发编制连续梁桥动力特性影响因素分析程序(以下简称DCBA程序)。鉴于MIDAS/CIVIL的后处理结果可以表格形式完全导出,DCBA程序可读取表格形式的计算数据,再将车辆速度,车辆数、桥面不平度或其他因素设为待分析因素,系统就可对影响桥梁动力学特性的每个因素的影响程度进行分析,从而达到免去正交试验的目的。
将本文中通过MIDAS/CIVIL分析得出的数据导入DCBA程序中,计算比较各个因素对桥梁动力学特性的影响程度。通过计算结果可以得出:
1) 对于跨中竖向位移的作用,各影响因素的主次关系依次为:车速,桥面不平度,行车数,即研究行车过程桥梁的挠度时,重点要考虑的是车速。
2) 对于跨中竖向加速度的影响,各个影响因素的主次关系依次为:桥面不平度,车辆速度,行车数,即研究跨中共振振幅时,首要应考虑桥面不平度。
3) 对于跨中弯矩系数的影响,各个影响因素的主次关系依次为:车速,桥面不平度,行车数,即研究跨中弯矩冲击力时,车速是首要的考虑因素。
4.2 DCBA程序应用效果对比
通过DCBA系统的分析比对,得出了各因素对梁动力特性的影响程度。为验证该程序计算结果的真实可靠度,利用最传统的正交试验法进行验算。由于要分析的是2因素10水平加1因素3水平的案例,其正交试验组至少需要设定上百组。为简化试验过程,将车速与行车数设定为3水平,这样只需设定3因素3水平的L9(33)的正交表即可。各因素水平取值详情及正交布置情况如表2所示。
表2所得出各因素的计算结果为极差,通过极差可以判别该试验组的影响程度。其中,对跨中弯矩冲击系数影响最大的组别为第8组,该组别的车速取的是试验范围数据内的峰值,而行车数和桥面平整度均为中间值,可见车速为对跨中弯矩冲击系数影响最大的因素。同理,对竖向加速度影响最大的为第5组,其桥面不平整度为组中峰值因素,对跨中竖向位移影响最大的为第8组,其影响程度最大的因素也是 车速。
由表2可见:通过正交试验所得结果与DCBA系统分析所得的最大影响因素结果基本相同,故DCBA程序可有效的分析各影响因素的影响程度,结果有较高的可靠度。

表2 梁动力特性影响因素正交计算结果
5 结论
1) 利用有限元的数值分析结果,根据接触点位移协调条件,建立车−桥耦合系统运动方程组,分析了车辆速度、行车数和桥面不平整度3个因素对桥梁的动力特性的影响规律。
2) 各因素对桥梁动力特性的影响变化规律不统一,但动力特性随车辆速度的增加、行车数的增加、桥面不平整度的降低整体呈上升趋势。
3) 编写DCBA程序,该程序可用于车−桥耦合系统中分析各影响因素对桥梁动力特性指标的影响程度。
4) 车辆速度对跨中竖向位移的影响最大,桥面不平度对跨中竖向加速度的影响最大,跨中弯矩冲击系数受车辆速度的影响最大。
[1] 李小珍, 张黎明, 张洁. 公路桥梁与车辆耦合振动研究现状与发展现状[J]. 工程力学, 2008, 25(3): 230−240.
LI Xiaozhen, ZHANG Liming, ZHANG Jie. State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridges system[J]. Engineering Mechanics, 2008, 25(3): 230−240.
[2] 郗艳红, 毛军, 高亮, 等. 横风作用下高速列车转向架非定常空气动力特性[J]. 中南大学学报(自然科学版), 2014, 45(5): 1705−1714.
XI Yanhong, MAO Jun, GAO Liang, et al. Aerodynamic force moment for high-speed train bogie in crosswind field [J]. Journal of Central South University (Science and Technology), 2014, 45(5): 1705−1714.
[3] 李永乐, 向活跃, 廖海黎. 基于风−车−桥(线)耦合振动的风屏障防风效果研究[J]. 土木工程学报, 2014, 47(3): 97−102.
LI Yongle, XIANG Huoyue, LIAO Haili. Study on wind shielding effect of wind screens based on coupling vibration theory of wind-vehicle-bridge(lines) systems[J]. China Civil Engineering Journal, 2014, 47(3): 97−102.
[4] AU F T K, LOU P, LI J, et al. Simulation of vibrations of Ting-Kau bridge due to vehicular loading from measurements[J]. Structural Engineering and Mechanics, 2011, 40(4): 471−488.
[5] 韩万水, 陈艾荣. 随机车流下的风−汽车−桥梁系统空间耦合振动研究[J]. 土木工程学报, 2008, 41(9): 97−102.
HAN Wanshui, CHEN Airong. Three-dimensional coupling vibration of wind-vehicle-bridge system under random traffic flow[J]. China Civil Engineering Journal, 2008, 41(9): 97−102.
[6] LADISLAV F B, YAU J D. Suspended bridges subjected to moving loads and support motions due to earthquake[J]. Journal of Sound and Vibration, 2009, 319(1/2): 218−227.
[7] YANG Y B, WU S. Dynamic stability of trains moving over bridges shaken by earthquakes[J]. Journal of Sound and Vibration, 2002, 258(1): 65−94.
[8] 李忠献, 黄健, 张媛, 等. 地震作用对轻轨铁路车桥系统耦合振动的影响[J]. 地震工程与工程振动, 2005, 25(6): 183−188.
LI Zhongxian, HUANG Jian, ZHANG Yuan, et al. Influence of seism is excitation on coupled vibration of train-bridge system in light railway[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(6): 183−188.
[9] 谭长健, 祝兵. 地震作用下高速列车与桥梁耦合振动分析[J]. 振动与冲击, 2009, 28(1): 4−9.
TAN Changjian, ZHU Bing. Coupled vibration analysis of high speed train and bridge subjected to seismic excitation [J]. Journal of Vibration and Shock, 2009, 28(1): 4−9.
[10] 王少林, 翟婉明. 地震作用下高速列车−线路−桥梁系统动力响应[J]. 西南交通大学学报, 2011, 46(1): 56−67.
WANG Shaolin, ZHAI Wanming. Dynamic responses of high-speed train-track-bridge system under seismic excitations[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 56−67.
[11] 王高新, 丁幼亮, 王晓晶, 等. 苏通大桥扁平钢箱梁温度场长期监测与统计分析[J]. 公路交通科技, 2012, 31(2): 69−73.
WANG Gaoxin, DING Youliang, WANG Xiaojing, et al. Long term monitoring and statistical analysis of temperature field of flat steel-box girder of Sutong Bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 31(2): 69−73.
[12] LEGER P, IDE I M, PAULTRE P. Multiple support seismic analysis of large structures[J]. Computers and Structures, 1990, 36(6): 1153−1158.
[13] 韩万水, 马麟, 院素静. 路面粗糙度非一致激励对车桥系统耦合振动响应影响分析[J]. 土木工程学报, 2011, 44(10): 81−90.
HAN Wanshui, MA Lin, YUAN Sujing. Analysis of the effect of inconsistent stimulus of surface roughness on vehicle-bridge coupling vibrations[J]. China Civil Engineering Journal, 2011, 44(10): 81−90.
[14] 刘波, 王有志, 王涛, 等. 大件运输中简支梁桥的动力响应分析及监测[J]. 哈尔滨工程大学学报, 2014, 35(3): 313−319.
LIU Bo, WANG Youzhi, WANG Tao, et al. Dynamic response analysis and monitoring of a simply supported bridge in oversize transport[J]. Journal of Harbin Engineering University, 2014, 35(3): 313−319.
[15] 刘献栋, 邓志党, 高峰. 公路路面不平度的数值模拟方法研究[J]. 北京航空航天大学学报, 2003, 29(9): 843−846.
LIU Xiandong, DENG Zhidang, GAO Feng. Research on the method of simulating road rough ness numerically[J]. Journal of Beijing University of Aero-nautics and Astronautics, 2003, 29(9): 843−846.
(编辑 陈爱华)
Analysis of influences of different factors on continuous rigid frame bridges based on theory of vehicle-bridge system coupling vibration
ZHANG Xiangdong, DU Dongning, CHAI Yuan, LIU Jiaqi
(College of Civil Engineering and Transportation, Liaoning Technical University, Fuxin 123000, China)
Based on analysis for the bridge and vehicle models, the motional equation sets of vehicle-bridge system coupled with vibration were set up considering the condition of the displacement compatibility at the contact point of wheel and bridge panel. The MIDAS/CIVIL software was used for analyzing the dynamic properties of the bridge under different conditions. The results show that the influences of different factors on the main bridge indices, e.g. the vertical displacement, impact coefficient of moment, and vertical acceleration at the mid-span of bridge, etc. Then the vibration-coupledvehicle-bridge system program that can analyze the factors on the main bridge indices was compiled. And this program was employed to analyze the dynamic properties of bridge. The results show that the vehicle speed, the number of vehicle, and the surface roughness of bridge have influences on the dynamic properties of bridge. The vehicle speed and the surface roughness of bridge play the key roles on the vertical displacement and vertical acceleration at the mid-span respectively. The vehicle speed also has a maximum influence in the impact coefficient of moment at the mid-span. Moreover, the reliability of this program is validated by the orthogonal experiment.
vehicle-bridge coupling; dynamic behavior; influence factor; finite element method
10.11817/j.issn.1672-7207.2016.08.041
U441.3
A
1672−7207(2016)08−2848−07
2015−10−08;
2015−12−19
国家自然科学基金资助项目(50978131);高等学校博士学科点专项科研基金资助项目(20112121110004) (Project (50978131) supported by the National Natural Science Foundation of China; Project(20112121110004) supported by China Postdoctoral Science Foundation)
张向东,教授,博士生导师,从事土木工程研究;E-mail:jwd101@126.com

