初始缺陷对除尘器壳体立柱轴压稳定性的影响

王登峰，贾文文，王元清，戴海金



初始缺陷对除尘器壳体立柱轴压稳定性的影响

王登峰1，贾文文1，王元清2，戴海金3

(1. 江南大学环境与土木工程学院，江苏无锡，214122；2. 清华大学土木工程系，北京，10084；3. 福建龙净环保股份有限公司，福建龙岩，364000)

为考虑除尘装备壳体加劲钢板墙板−H型钢立柱结构体系中初始缺陷的影响，采用非线性有限元方法，研究初始几何缺陷和焊接缺陷对立柱承受轴向压力时失稳模态和稳定承载力的影响。研究结果表明：较为不利的初始几何缺陷形态是立柱截面的初始弯扭变形，较为不利的发生最大初始几何变形的位置在靠近柱顶的高轴力区。焊接残余变形对壳体立柱轴压稳定性影响很小，焊接残余应力对壳体立柱稳定性有微小的有利影响。构建壳体立柱轴压稳定性数值计算模型时，可以引入施加定向干扰的完善结构极值点模态缺陷，以充分考虑初始几何缺陷影响；无需考虑焊接残余应力影响。

结构工程；除尘器壳体；墙板−立柱结构体系；稳定性；非线性有限元；初始几何缺陷；焊接缺陷

除尘器广泛应用于电力、冶金、化工和建材等行业中用以消除大气烟尘，是治理雾霾污染的重要环保装备。国内外对除尘器工艺研究较多，但对其支承结构的承载机理研究甚少。壳体是除尘器中最重要的工艺部件。大型除尘器壳体的侧面围护结构常采用加劲钢板墙板−H型钢立柱结构体系。加劲钢板和立柱通过连续焊接连接。墙板主要起封闭围护作用，承受由空气负压和风荷载等引起的横向荷载；立柱作为支承骨架承担由墙板传递来的横向荷载和由壳体顶梁传递来的竖向荷载，实际为一压弯构件。由于立柱和墙板连续连接形成共同受力的整体，墙板可以发挥受力蒙皮作用，一方面为立柱分担荷载，另一方面为立柱提供侧向支撑，提高其稳定性，因此对壳体立柱稳定性研究需要考虑墙板受力蒙皮作用。关于受力蒙皮结构国内外学者取得了一些研究成果。DAVIES等[1]在大量试验的基础上进行了理论分析，提出了确定受力蒙皮剪切柔度和强度的计算方法，即将组成受力蒙皮各个部件在荷载作用下的柔度叠加起来得到整个蒙皮的柔度，强度的计算方法是根据他们提出的计算假定，计算可能发生破坏的部位，取破坏荷载最小值作为最大设计荷载。WRIGHT等[2]研究表明蒙皮板与支承框架间的连接类型和布置方式对蒙皮板受剪性能有重要影响。LUCAS等[3−4]研究冷成型檩条−蒙皮板结构的计算模型，一种是包括檩条和蒙皮板的完全模型，另一种是仅建有檩条的简化有限元模型，在简化模型中蒙皮板的剪切和转动刚度以弹簧形式施加到檩条与蒙皮板连接边上，通过设置合理的弹簧参数，2种模型计算结果均与试验吻合良好。朱勇军等对蒙皮支撑构件进行系统研究，用非线性有限元方法研究蒙皮抗剪刚度、扭转约束、构件长细比和荷载偏心对蒙皮支撑轴心受压构件受力性能的影响[5−6]；用非线性有限元法研究了蒙皮支撑梁间距、跨度、构件截面开口方向及构件初始扭转对蒙皮支撑梁静力性能的影响[7]。舒兴平等[8]用试验方法研究了风吸力作用下的蒙皮支撑檩条的稳定性。关于缺陷对受力蒙皮结构承载性能影响研究的可见文献极少，相关研究主要集中于缺陷对加劲板结构稳定性的影响。PAULO等[9]采用有限元方法研究几何缺陷对加劲铝合金板承受轴向压力时承载力的影响，发现缺陷模态和缺陷幅值对承载力影响较大；同时研究发现焊接区域材料性能变化对板件承载力几乎没有影响[9]。罗晓玲等[10]用非线性有限元方法研究了不同的缺陷幅值、加劲形式、加载方式及边界条件对加劲板的稳定性影响。康孝先等[11]从含初始弯曲的大挠度方程出发，以薄板厚度的折减量为摄动参数，将残余应力考虑成等效荷载，得出板的极限承载力方程。王彦博等[12]进行了高强钢焊接H 形柱轴心受压极限承载力研究，认为考虑构件初始弯曲、荷载初始偏心和残余应力的有限元模型可以较准确地预测轴心受压柱的极限承载力。对于实际为压弯构件的壳体立柱，作为研究基础，首先研究其承受柱顶轴向压力作用下的稳定性。壳体结构各部件在制作、运输和安装过程中不可避免会产生初始缺陷，对壳体立柱轴压稳定性研究必须考虑这些缺陷的影响。作为壳体立柱在轴向压力作用下稳定性数值研究的基础，需要研究各种可能形式缺陷的影响，找出最不利缺陷形态，继而提出可以充分考虑缺陷影响的壳体立柱轴压稳定性计算模型构建方法。本文作者通过非线性有限元方法研究不同形态几何缺陷与焊接缺陷对壳体立柱轴压稳定性的影响，并据此提出了可以充分考虑缺陷影响的壳体立柱轴压稳定性计算模型构建方法。

1 研究模型

1.1 结构模型

本文以实际工程中的除尘器壳体墙板−立柱结构体系为研究背景。实际结构内一般1个跨墙板对应1个电场，为简化计算模型，本文分析仅取2个跨墙板建模，立柱高度，加劲钢板墙板宽度，墙板壁厚。墙板与H型钢立柱一侧翼缘通过连续焊缝连接，本文定义与墙板连接的立柱翼缘为后翼缘，远离墙板一侧翼缘为前翼缘。为提高立柱稳定性，壳体内等间距设置中部撑杆与立柱后翼缘连接，对其提供垂直墙板平面的约束，撑杆间距为。壳体墙板−立柱结构体系和位移坐标系如图1所示。壳体两侧边缘立柱与刚度较大的烟气进、出口连接，受约束比壳体中间立柱更强，而承担的荷载水平一般低于中间立柱，因此，壳体边缘立柱稳定性一般优于中间立柱。本文研究壳体中间立柱在轴向荷载作用下的稳定性。

图1 壳体墙板−立柱结构体系示意图与位移坐标系

1.2 有限元模型

本文采用通用有限元程序ANSYS进行分析。所有结构部件均采用壳单元SHELL181模拟。材料模型采用理想弹塑性模型，弹性模量=2.06×105MPa，泊松比=0.3，壳体采用Q235钢材制作，屈服强度为y=235 MPa。①和③号柱柱底约束向和向平动自由度，②号柱柱底约束3个方向平动自由度。考虑到实际结构中有中部撑杆对立柱提供向的支撑，有限元模型在立柱与撑杆连接位置对立柱后翼缘施加向平动约束。壳体墙板在顶部与加劲顶板连续连接，因此壳体墙板顶部边界施加向平动约束。分析过程中对②号柱柱顶施加均布竖向荷载至结构破坏。考虑几何非线性效应，用弧长法跟踪结构响应路径。

1.3 网格精度测试

为保证计算结果的准确性，首先进行网格划分精度的试算。取产生单元较多的墙板区域两道加劲肋之间的板块作为四边简支板，一侧板边施加单向均布压力，将有限元计算得到的特征值屈曲荷载与经典解比较，误差不超过1%时，认为网格精度满足要求。单向均匀受压简支板的弹性经典屈曲荷载cr按下式计算[13]：

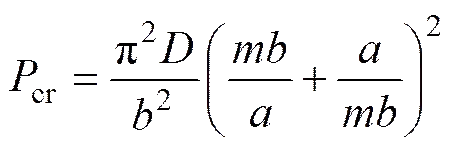
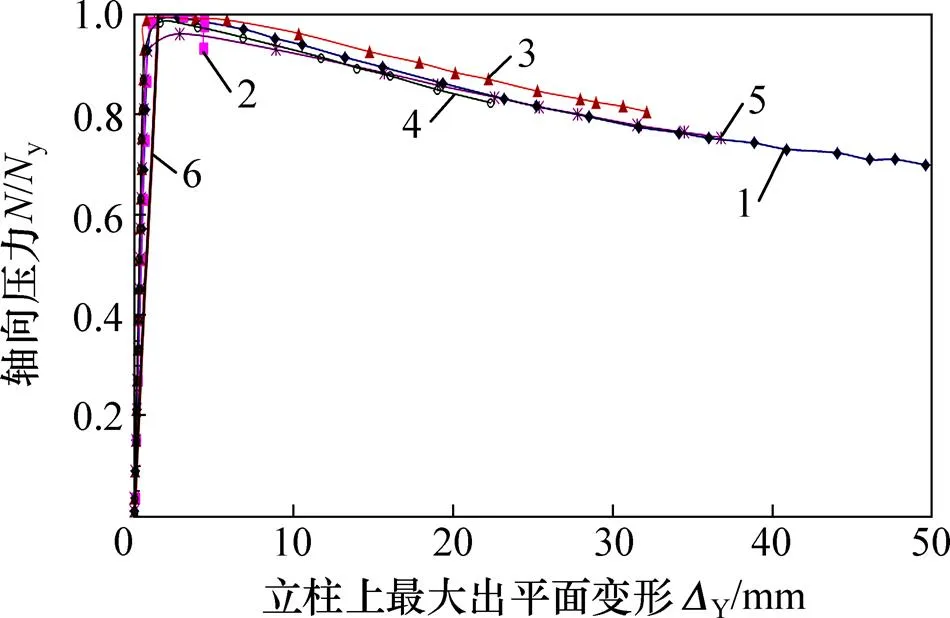
立柱截面网格划分会影响立柱稳定性计算结果。对一例带有正弦半波形初始几何缺陷的壳体立柱结构进行不同网格精度下的非线性计算，其轴向荷载−立柱上最大出平面位移曲线如图2所示。由图2可知：立柱翼缘半宽度内划分2个网格时，柱顶荷载可以达到全截面屈服荷载y(y=y，为立柱截面积)，没有明显屈曲变形发生。当立柱翼缘半宽度内划分3~5个网格时，柱顶极限荷载均达不到y，3种情况下的极限承载力相差不超过0.5%。达到极限荷载时，3种情况立柱上都有明显失稳发生，失稳模态类似，划分4个网格的情况和划分5网格情况对应的荷载−位移曲线基本重合，而仅划分3个网格时的结构刚度略大。为保证承载能力和变形的计算精度，同时考虑计算效率，后续分析对于立柱半翼缘宽度内划分4个网格，腹板网格尺寸取翼缘网格边长乘以腹板高度与翼缘宽度比值。

1—半翼缘宽度设2网格；2—半翼缘宽度设3网格；3—半翼缘宽度设4网格；4—半翼缘宽度设5网格。

H294×200×12×8，=17.02 m，=6 mm，=4 010 mm，=3 110 mm

图2 不同网格划分精度时的荷载−位移曲线比较

Fig. 2 Load−displacement curves for models with different mesh densities

1.4 有限元分析方法验证

为了验证本文有限元分析方法的正确性，根据参考文献[14]中编号为H1试件的几何构造建立有限元模型，钢材采用理想弹塑性模型，进行试验过程的非线性数值模拟。试件为2根Z型檩条，上翼缘连接压型钢板，檩条两端简支，通过在压型钢板上堆放砖块加载。试验得到檩条截面最大抵抗弯矩为14.66 kN∙m，有限元计算值为13.10 kN∙m。有限元计算中没有考虑材料的应变硬化，而实际结构有一定的塑性储备，这可能是计算值比试验值稍低的原因。可以认为本文的有限元计算分析方法能够较为准确地模拟墙板−立柱结构体系的非线性响应。

2 初始几何缺陷对壳体立柱稳定性的影响

初始几何缺陷对钢构件稳定性会有影响。尽管受壳体墙板支撑，壳体立柱仍有可能发生失稳破坏。为诱发立柱失稳以研究其稳定性影响规律，同时研究不同形式初始几何缺陷对立柱稳定性的影响，本文构建了多种立柱初始几何缺陷模态，研究带有不同缺陷模态的壳体立柱失稳模态和稳定承载力，并探究最不利初始几何缺陷模态。

2.1 正弦半波形几何缺陷模态

壳体H型钢立柱为双轴对称截面，独立工作的双轴对称轴心受压构件对正弦半波初始弯曲几何缺陷敏感，会呈现弯曲失稳。为诱发壳体立柱发生弯曲失稳，首先对中间立柱构建了5种正弦半波形几何缺陷模态，分别为：墙板平面外正对称正弦半波缺陷模态(缺陷模态a)、墙板平面外反对称正弦半波缺陷模态(缺陷模态b)、墙板平面内正对称正弦半波缺陷模态(缺陷模态c)、墙板平面内反对称正弦半波缺陷模态(缺陷模态d)以及复合了墙板平面内、外反对称正弦半波的螺旋形状缺陷模态(缺陷模态e)。缺陷模态a~d的几何构形如图3所示。缺陷模态(a)和(b)的缺陷函数为δ=|0sin(π/)|；缺陷模态(c)和(d)的缺陷函数为δ=|0sin(π/)|。其中，0为缺陷幅值，取/1 000。建立有限元模型时首先构建带有缺陷的壳体中间立柱，边缘两侧立柱为完善结构，通过蒙皮方法构建墙板。

(a) 墙板平面外正对称正弦半波模态；(b) 墙板平面外反对称正弦半波模态；(c) 墙板平面内正对称正弦半波模态；(d) 墙板平面内反对称正弦半波模态

图3 正弦半波形缺陷模态示意图

Fig. 3 Schematic diagram of geometrical imperfectionswith half-wave sine shape

对于一例具有工程背景的典型结构首先进行完善结构的计算分析，完善结构壳体立柱上施加的荷载可以达到全截面屈服荷载，达到屈服荷载时立柱靠近顶部区域发生弯扭变形，幅值较小。进行带有5种不同立柱正弦半波形缺陷模态的缺陷结构计算分析，其荷载−立柱上最大出墙板平面位移曲线如图4所示。由图4可知：缺陷结构立柱顶施加的极限荷载u(定义为缺陷结构的稳定承载力)均达不到y，以复合了墙板平面内、外反对称正弦半波的螺旋形状缺陷模态e承载力为最低，比完善结构之值降低4.0%，说明缺陷对立柱承载力是有影响的。对于缺陷结构，当荷载达到u时，立柱在靠近顶端区域发生明显失稳，5种缺陷结构的失稳模态类似，带有缺陷模态e的壳体立柱失稳模态如图5(a)所示，图中深色部分显示的是轴压应力达到屈服点的区域。可见：由于受墙板约束，后翼缘变形不大；立柱顶端下方的前翼缘在高压应力下发生较大的侧向弯曲(绕截面轴)和扭转变形；腹板发生较大扭转变形。此处立柱截面发生翘曲变形，不再保持一平直截面。发生最大位移处立柱截面变形后形状如图5(b)所示(图中虚线表示未变形截面)。可见：在失稳过程中，立柱截面形状发生改变，不再保持H形周边。带有此类缺陷的壳体立柱破坏呈现为柱顶下方区域弹塑性弯扭失稳。

1—缺陷模态a；2—缺陷模态b；3—缺陷模态c；4—缺陷模态d；5—缺陷模态e；6—完善结构。

H294×200×12×8，=17.02 m，=6 mm，=4 010 mm，=3 110 mm

图4 不同正弦半波形缺陷结构的荷载−位移曲线比较

Fig. 4 Comparison among load-displacement curves of models with different half-wave sine shape imperfections

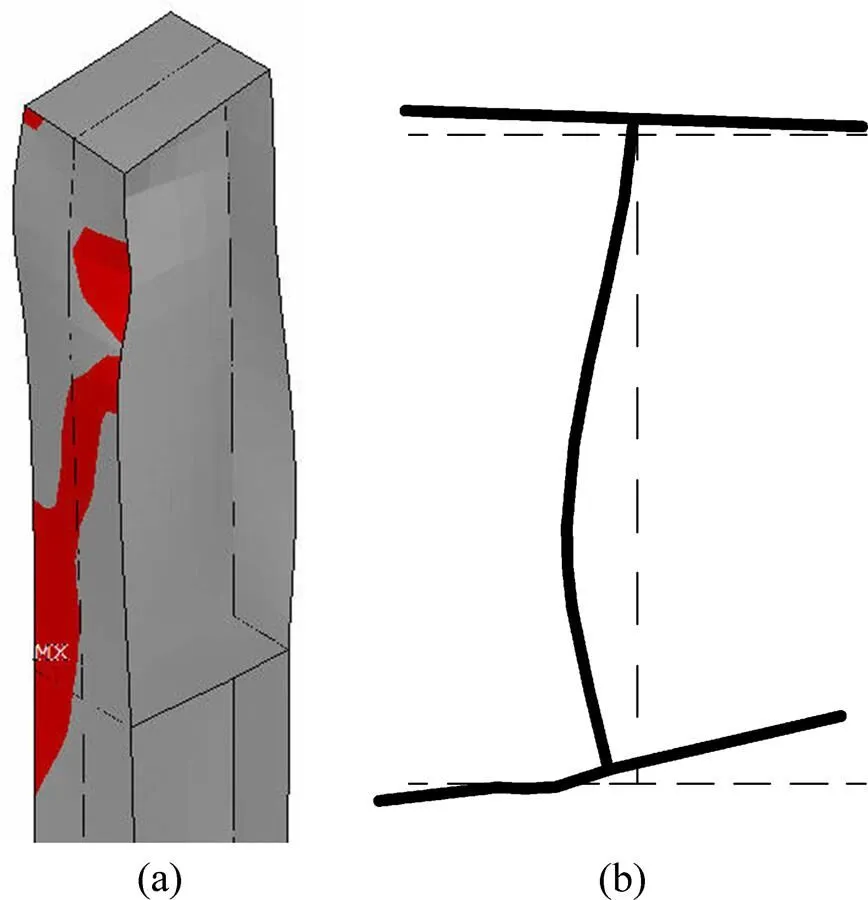
(a) 立柱失稳模态；(b) 立柱截面变形

图5 立柱弯扭失稳模态

Fig. 5 Flexural-distortional buckling mode of column

2.2 复合极值点变形形态的正弦半波形几何缺陷 模态

立柱上正弦半波初始缺陷模态中仅考虑了立柱轴线构形的初始弯曲，没有考虑截面形状的初始缺陷，这与立柱最终发生的失稳模态并不符合。结构往往对与最终实际发生的失稳模态相一致的初始缺陷模态会比较敏感。此外，墙板平面内的正弦半波形缺陷模态没有考虑墙板的初始缺陷，而墙板上的缺陷会影响墙板刚度，继而影响立柱稳定性，缺陷结构中应包含墙板缺陷。因此，通过2步操作构建带有复合了极值点变形形态的正弦半波形几何缺陷模态的结构计算模型：第1步，建立带有正弦半波形态初始几何缺陷的壳体墙板−立柱结构体系计算模型，并加载至极限荷载；第2步，根据荷载达到极值点时的结构构形，修正壳体结构计算模型内各结点坐标，得到目标缺陷模型。通过调整第1步中正弦半波初始缺陷幅值和第2步中坐标修改比例系数，可以使得最终的缺陷模型中立柱上初始缺陷幅值0为/1 000。将上述5种正弦半波形缺陷结构分别复合对应的极值点变形形态，构造出5种复合了极值点变形形态的正弦半波形几何缺陷模态，其编号依次对应设为缺陷模态a′~e′(缺陷模态a′指在缺陷模态a基础上复合对应的极值点变形形态，其余编号方式类同)。这样的缺陷模态既考虑了立柱轴线构形的初始弯曲，又考虑了与最终失稳模态相一致的截面形状的初始缺陷，同时考虑了墙板几何缺陷。

带有复合了极值点变形形态的正弦半波形几何缺陷模态结构柱顶轴压荷载−立柱上最大出墙板平面位移曲线如图6所示(模型几何尺寸特征与图4反映结构相同)。由于考虑了截面形状的初始变形，会促进立柱靠近顶部区域失稳的发生。计算结果表明，复合了极值点变形形态的正弦波形缺陷结构立柱稳定承载力比对应的仅有正弦波形缺陷结构之值降低1.4%~3.2%，其中以带有缺陷模态e′的结构稳定承载力最低，为0.942y，可见复合了极值点变形形态的正弦半波形缺陷模态对于立柱轴压稳定性是更为不利的。带有此类缺陷模态结构失稳模态与正弦半波形缺陷结构类似，仍然呈现柱顶下方区域立柱前半部分截面弹塑性弯扭失稳，不过达到稳定承载力时，屈曲变形值会增大。

1—缺陷模态a′；2—缺陷模态b′；3—缺陷模态c′；4—缺陷模态d′；5—缺陷模态e′；6—缺陷模态f；7—缺陷模态g；8—完善结构。

H294×200×12×8，=17.02 m，=6 mm，=4 010 mm，=3 110 mm

图6 带有不同缺陷模态结构的荷载−位移曲线比较

Fig. 6 Comparison among load−displacement curves of models with different geometrical imperfection modes

2.3 完善结构的极值点缺陷模态

取完善结构达到极限荷载时的变形形态作为初始几何缺陷模态，缺陷幅值0取/1000，定义为完善结构的极值点缺陷模态，编号缺陷模态f。带有此种缺陷结构的荷载−位移曲线如图6所示。由图6可知：其稳定承载力比复合了极值点变形形态的正弦半波形缺陷结构的承载力更低，为0.925y。其失稳模态仍为柱顶下方区域弯扭失稳。当立柱缺陷幅值一定时，完善结构极值点缺陷模态主要反映立柱在顶部下方约0.4处区域的截面初始弯扭变形，其初始弯扭变形最大值为0.70。而复合了极值点变形形态的正弦半波形缺陷模态主要包含立柱的初始整体弯曲和柱顶下方区域截面初始弯扭2种初始几何变形，其中截面初始弯扭变形最大值不到0.40。由此可以推断，一方面，柱顶下方区域立柱截面的初始弯扭变形对于立柱轴压稳定性更加不利；另一方面，对于立柱截面初始弯扭变形这一缺陷模态，随着缺陷幅值增大，立柱稳定承载力明显下降。

2.4 缺陷位置对立柱稳定性的影响

上述研究主要比较了不同初始几何缺陷模态对于立柱稳定性的影响，没有考虑发生最大缺陷位置的影响。为了考查立柱上发生最大初始几何变形位置对于其稳定性的影响，设计了几组不同参数结构模型进行计算比较，模型结构参数如表1所示。定义壳体立柱的稳定系数=u/y，各模型带有不同缺陷模态时的稳定系数如表2所示。

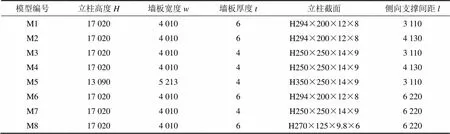
表1 不同计算模型参数