锚索锚固质量检测的应力波法试验研究

邓东平，李亮，高连生



锚索锚固质量检测的应力波法试验研究

邓东平，李亮，高连生

(中南大学土木工程学院，湖南长沙，410075)

在较长锚索中利用应力波法难以在锚索端头接收到反映锚固体断面变化处的有效应力波信号，以3种特殊形式锚固体(全长注浆型锚固体、存在缺陷段全长注浆型锚固体和存在自由段非全长注浆型锚固体)实际模型为基础，采用锚索端头和底端分别激发应力波信号这2种方式，通过实测应力波振动速度，并与理论分析结果进行对比，验证应力波法检测锚索锚固质量的可靠性。然后，结合锚索端头和底端分别激发应力波信号这2种方式研究锚索端头和底端同时激发应力波信号方式对锚索锚固质量进行检测的可行性。研究结果表明：锚索端头和底端同时激发方式可对锚索锚固质量进行有效检测，且在锚索端头接收到的信号为反映锚固体断面变化处位置中传播路径最短的应力波信号；为了能够区分锚索端头和底端分别激发的应力波信号，建议这2种应力波信号采用不同频率。

锚索；锚固质量；应力波；激发方式；传播速度；特征线法

在锚索框架梁系统中，锚索上施加的预应力可有效地提高边坡的稳定性，故其成为边坡工程中一种常用的加固措施[1−2]。然而，锚索系统是一项隐蔽工程，因此，为确保施加在锚索上的预应力能够长期有效，需对锚索的施工质量进行检测。目前，针对锚索的锚固质量检测的方法有多种，但与传统的破坏试验法相比，应力波反射法[3−7]作为一种无损的检测方法在锚索锚固质量检测中获得了广泛应用，已形成一套成熟的质量现场测试技术并制定了相应的规程规范[8]。应力波反射法在锚索锚固质量检测中常在锚索端头激发应力波信号，并在锚索端头安装应力波信号接收装置来收集反映锚固体断面变化处位置信息的应力波信号，然后，通过分析接收的应力波波形、相位和时程来判断锚索的长度和缺陷段的位置[9−10]。尽管应力波反射法非常实用，但其存在一个重要的制约因素，是应力波在锚固体内传播过程中会出现不同程度的衰减，尤其是当锚索较长且锚固质量较好时，在锚索端头更难以接收到有效的应力波信号[11]。为了使得应力波法同样能够对较长锚索的锚固质量进行可靠检测，需缩短反映锚固体断面变化处信息的应力波信号在锚固体内的传播路径。为此，本文作者基于现场制作的3种特殊形式锚固体(全长注浆型锚固体、存在缺陷段全长注浆型锚固体和存在自由段非全长注浆型锚固体)实际模型，通过对比理论分析结果与现场试验结果，验证锚索端头和底端分别激发应力波信号这2种方式对锚索锚固质量检测的可靠性。同时，为了结合锚索端头和底端分别激发应力波信号这2种方式的优点以及在锚索端头获得反映锚固体断面变化处信息中传播时间最短的应力波信号，采用锚索端头和底端同时激发应力波信号方式并研究其对锚索锚固质量检测的可行性。

1 锚固质量检测应力波法理论分析

1.1 应力波传播的特征线法

在锚索结构系统中其长度方向的尺寸一般远远大于其他方向的尺寸，故可将锚索及外围注浆体所组合而成的锚固体简化为一维弹性体杆件进行动力学分析。应力波沿特征线传播计算模型如图1所示。在一维平面波中，D′ALEMBERT通过理论分析得到应力波的波动解为沿同一速度传播的1个右行波和1个左行波这2行波叠加的结果[12]，即应力波的波动解为：(，)=(−)+(+)(其中，为应力波在位置时刻的位移；为应力波在弹性体中的传播波速，；和分别为弹性体的弹性模量和质量密度)。若设=−和=+，且当和均为常数时，则在−平面上形成了和的2簇特征线，而F波即为沿特征线=−传播的右行波；G波即为沿特征线=+传播的左行波。

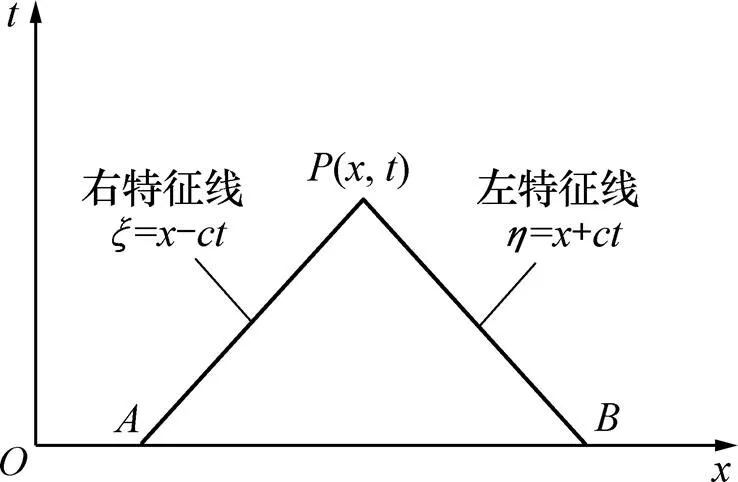
图1 应力波沿特征线传播计算模型

马宏伟等[13]通过分析应力波沿特征线传播的规律得到如下相容关系：

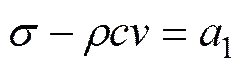
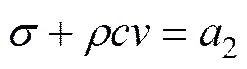
式中：1和2为常数；和分别为应力波在一维弹性杆件中相应断面位置上的应力和振动速度。

式(1)和(2)表明：当应力波沿右(或左)特征线传播时，若在同一弹性体中某个变量(应力或振动速度)不变，则其另一个变量(振动速度或应力)也不变；同时，若知右(或左)特征线上任一点的振动速度和应力，则可根据另一点的振动速度(或应力)求得该点的应力(或振动速度)。因此，由该相容关系便可根据已知的初始和边界条件来分析应力波在−平面上其他各点的应力和振动速度。

1.2 锚固组合体计算模型

锚固组合体计算模型如图2所示。锚固体由锚索和外围注浆体组合而成，其中，锚索的半径为，弹性模量为s及质量密度为s，外围注浆体的外半径为，弹性模量为c，质量密度为c。假定锚索和外围注浆体均为各向同性体，且锚固组合体在极小应力作用下不计泊松比的影响并处于弹性工作阶段[12]，同时，在锚索未张拉预应力前锚索端头小应力作用下注浆体外围的岩土体对锚固体影响较小，则可取单位长度的锚固组合体进行受力分析。由锚固组合体的力平衡条件、变形协调条件及材料的物理关系可得：

固组合体的弹性模量和质量密度；，s和c分别为锚固组合体、锚索和外围注浆体所受的应力；，s和c分别为锚固组合体、锚索和外围注浆体在各自应力作用下所发生的形变。

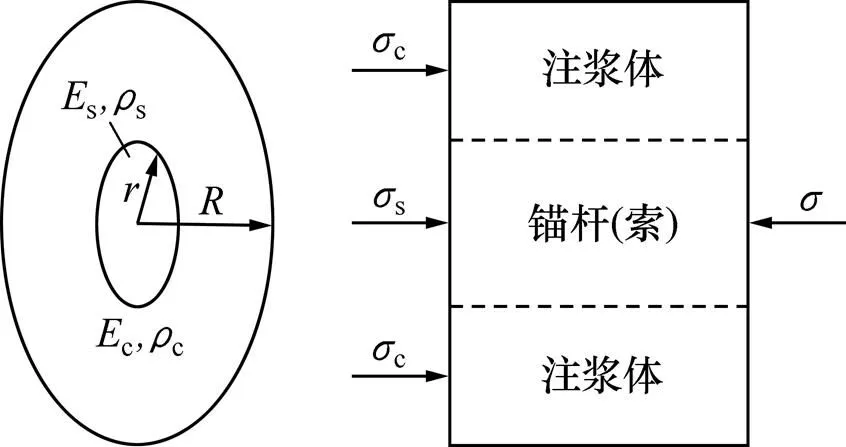
图2 锚固组合体计算模型

通过求解式(3)~(5)可得锚固组合体的弹性模量和质量密度如下：

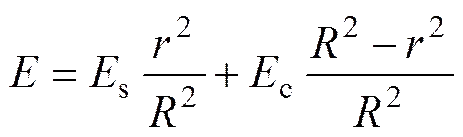
根据式(6)和(7)可得应力波在锚固组合体中的传播速度。

1.3 锚固体断面变化处应力波的反射与透射

当应力波在锚固体内的传播过程中若遇到锚固组合体的断面形状或性质发生变化(如锚索自由段与锚固组合体界面、锚固组合体中缺陷段断面、锚索端头或底端等)，则应力波会在锚固体断面位置变化处发生反射和透射，若此时在锚索端头接受这些反映锚固体断面变化信息的应力波信号，则可采用应力波法来判别锚索的长度和锚固体的缺陷段位置。应力波在锚固体断面变化处发生反射和透射计算模型如图3所示。将锚固体断面形状或性质发生变化的模型进行简化，其中，为锚固体断面发生变化处的界面，界面两侧分别为锚固体1和锚固体2；当应力波(图3中为右行波)从左向右传播时，应力波将在断面变化处界面上发生应力波的反射和透射。令右行到界面处的入射波为I、反射波为R，透射波为T，锚固体1的断面面积为1、弹性模量为1及质量密度为1，锚固体2的断面面积为2、弹性模量为2及质量密度为2。由锚固组合体在断面变化处的位移、速度和力的连续条件及一维应力波的波动方程[12]，可得反射波、透射波与入射波的应力和振动速度的关系式如下：

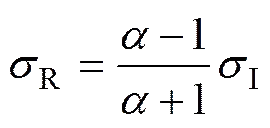
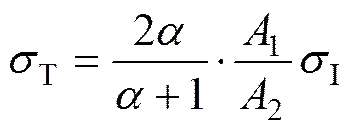
式中：I，R和T分别为入射波、反射波和透射波的应力；I，R和T分别为入射波、反射波和透射波的振动速度；为阻抗，=(22/02)/(11/01)，01和02分别为应力波在锚固体1和锚固体2中传播的速度，，。

图3 应力波在锚固体断面变化处发生反射和透射计算模型

1.4 几种特殊锚固体形式下的应力波传播参数分析

采用应力波法对锚索锚固质量进行检测，包括2方面内容：锚索的长度和缺陷段的位置。下面针对3种特殊锚固体形式进行分析。这3种特殊锚固体型式为：1) 全长注浆型锚固体；2) 存在缺陷段全长注浆型锚固体(如图4所示)；3) 存在自由段非全长注浆型锚固体。当采用2种应力波信号激发方式(锚索端头激发和锚索底端激发)时，在锚索端头接受应力波信号，然后利用理论方法来分析应力波在锚索端头接受到的应力波信号传播参数。同时，在实际检测过程中可以使用这些传播参数判别、计算锚索的长度和缺陷段的位置，对图4所示的存在缺陷段全长注浆型锚固体的质量进行检测。

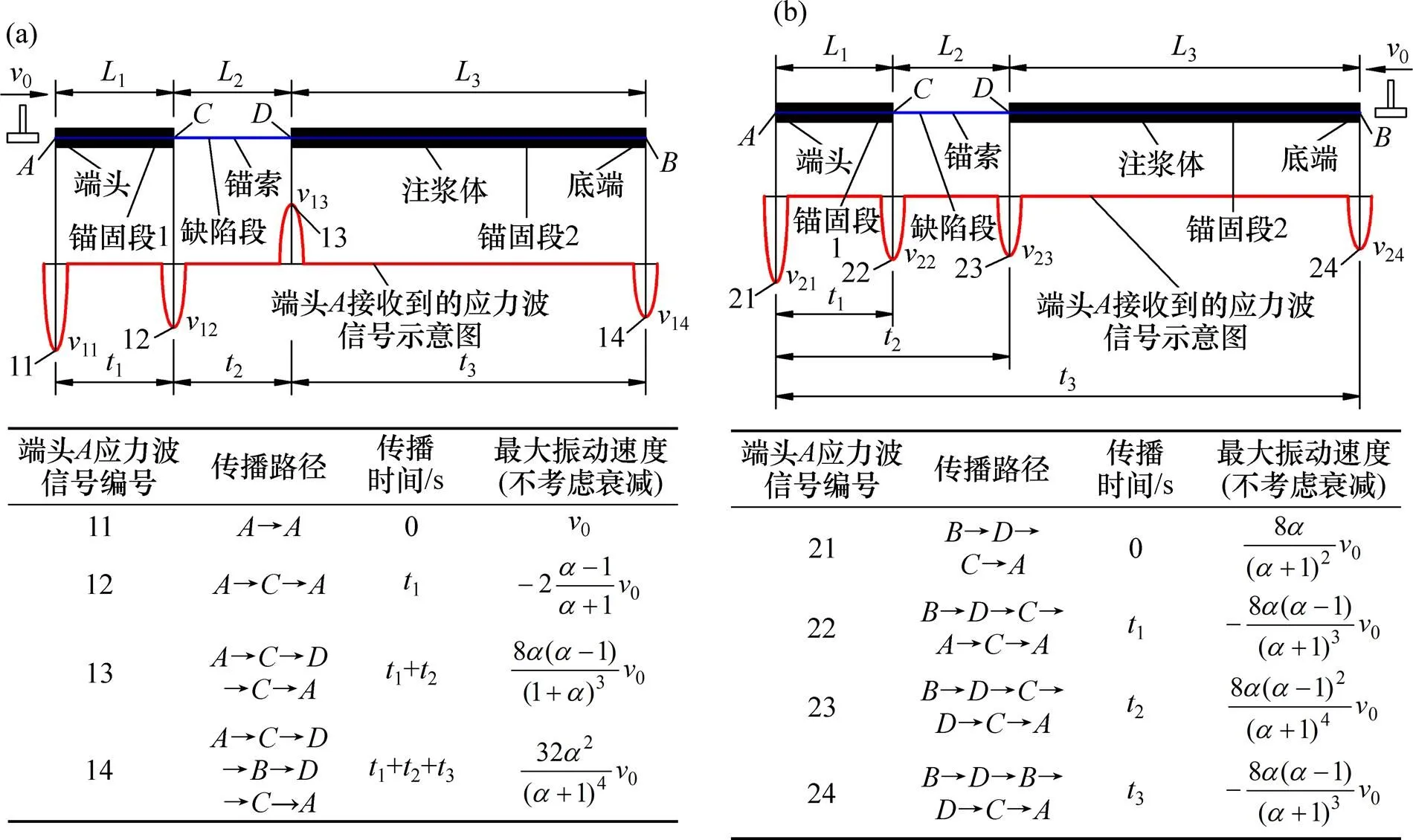
(a) 锚索端头激发方式；(b) 锚索底端激发方式

图4 存在缺陷段全长注浆型锚固体中应力波计算参数

Fig. 4 Calculation parameters of stress wave in full-length grouting anchorage body with existence of defective segment

取外围注浆体材料参数即弹性模量c、质量密度c及断面面积c，锚索的材料参数弹性模量s、质量密度s及断面面积s，根据前述理论分析便可得锚固组合体的材料参数即弹性模量、质量密度及断面面积。同时，若以小锤敲击方式在锚索端头或底端产生1个最大振动速度为0的应力波脉冲信号，则应力波信号在锚固体中来回传播并携带各断面变化处的信息。由于锚固组合体的端头和底端均为自由端，故在其上存在应力波的压力边界条件为=0 kPa。若不考虑应力波在锚固体内传播过程中出现的能量衰减，则可根据前述应力波的特征线法及应力波在断面变化处反射、透射与入射的对应关系，得到端头接收到关于锚固体断面变化处及底端反射或透射回的应力波信号与初始应力波信号的相对大小及相位关系，并采用应力波的振动速度表示。

当应力波由锚固段传播到锚索自由段时，设在该交界面上的阻抗为，在各材料参数一致、应力波由锚索自由段传播到锚固段时，此交界面上的阻抗为1/，其中，=(ss/s)/(/)。同时，由一般情况下锚索和外围注浆体(水泥砂浆)的材料参数取值范围，可知＜1。

对于全长注浆型锚固体，其全长为，0为锚固段长度范围内应力波往返所需的传播时间；对于存在缺陷段全长注浆型锚固体，其锚固段1长为1，缺陷段长为2(缺陷段的注浆饱满度为0，即表明该段未注浆)，锚固段2长为3，如图4所示。图4中：1，2和3分别为锚固段1、缺陷段和锚固段2长度范围内应力波往返所需的传播时间；对于存在自由段非全长注浆型锚固体，其自由段长度为4，锚固段长度为5，4和5分别为自由段和锚固段长度范围内应力波往返所需的传播时间。由此，当给定应力波在锚固体和锚索中的理论传播速度时，可根据应力波在各段上传播所需的时间来计算锚索的长度和缺陷段的位置(或各段的长度)；或当各段长度已知时，可以分析应力波在各段上的实际传播速度，并与理论结果进行对比验证应力波法检测锚索锚固质量的可行性。

2 锚固质量检测应力波法现场试验

2.1 现场试验方案

锚固体质量检测现场试验与计算简化模型如图5所示。与前述理论分析结果一致，在现场同样制作3种特殊形式的锚固体(全长注浆型锚固体、存在缺陷段全长注浆型锚固体(其中，缺陷段的注浆饱满度为0)和存在自由段非全长注浆型锚固体)。在实际模型中，也采用小锤在锚索的端头或底端分别进行敲击，并在锚索端头处放置应力波信号接收器来分别接受这2种激发方式所传递的应力波信号。同时，为了便于现场制作，将外围注浆体浇筑成横断面边长为100 mm的正方形。

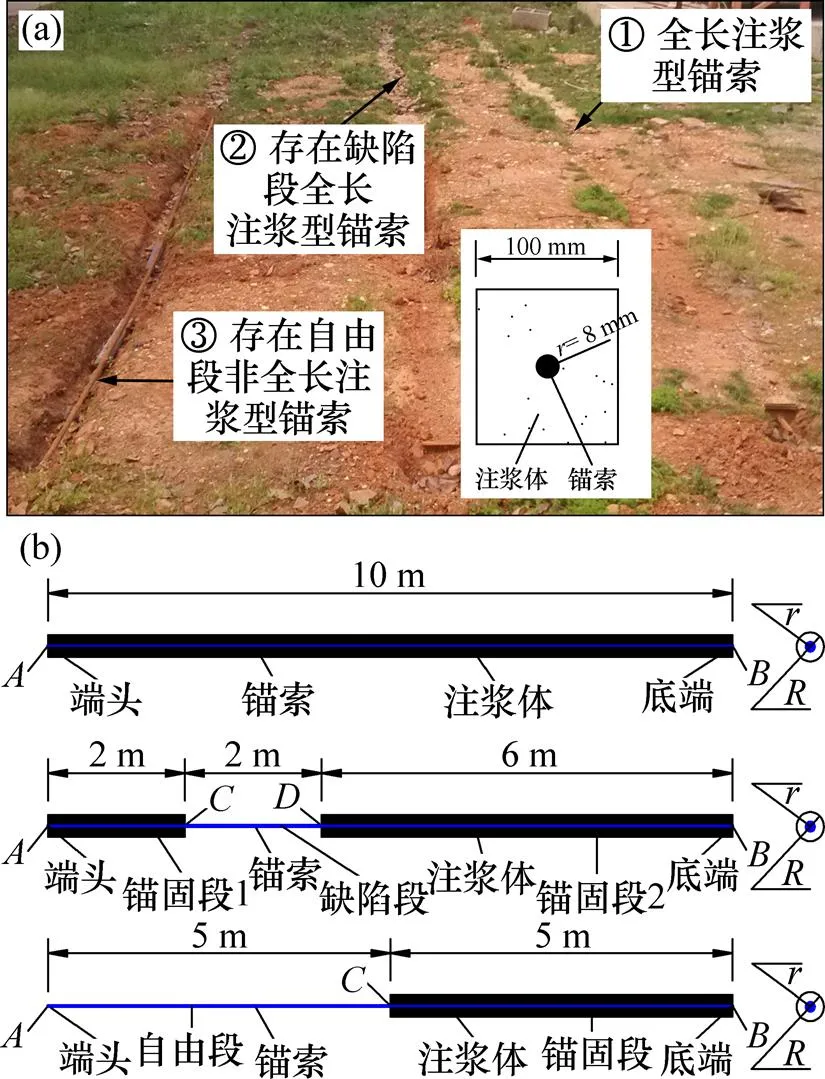
(a) 现场试验模型；(b) 计算简化模型

图5 锚固体质量检测现场试验与计算简化模型

Fig. 5 Field test for detecting quality of anchorage body and simplified calculation model

将现场试验模型简化为计算模型(如图5(b)所示)。其中，锚索的半径=8 mm，并按照面积等效原理将外围注浆体的横断面等效为内径为和外径为的圆环(=56.419 mm)。与实际模型一致，全长注浆型锚固体其全长=10 m，存在缺陷段全长注浆型锚固体(缺陷段的注浆饱满度为0)，其锚固段1长为1=2 m，缺陷段长为2=2 m；锚固段2长为3=6 m，存在自由段非全长注浆型锚固体其自由段长为4=5 m，锚固段5= 5 m。

2.2 试验材料参数

锚固体的外围注浆体为C32.5普通硅酸盐水泥、河沙(过2 mm圆孔筛)和自来水按其质量比为1.0:1.0:0.6而制成的水泥砂浆。根据文献[14−16]，可知外围注浆体(即水泥砂浆)的弹性模量c=1.4×1010Pa，质量密度c=2 400 kg/m3；锚索的弹性模量s=2×1011Pa，密度s=7 800 kg/m3。因此，按照前述锚固组合体的计算公式可得锚固体的材料弹性模量=2.896×1010Pa，质量密度=2 834.294 kg/m3。

3 现场试验结果分析

在实际锚固体模型中，对上述3种特殊形式锚固体的锚索端头和底端分别采用小锤人工激发应力波信号，此时锚索端头接受的应力波信号分别如图6(全长注浆型锚固体)、图7(存在缺陷段全长注浆型锚固体)和图8(存在自由段非全长注浆型锚固体)所示。

(a) 锚索端头激发方式；(b) 锚索底端激发方式；(c) 锚索端头和底端同时激发方式

图6 全长注浆型锚固体应力波法质量检测时锚索端头应力波信号

Fig. 6 Stress wave signals on top of anchor cable asadopting stress wave method to detect anchorage quality infull-length grouting anchorage body

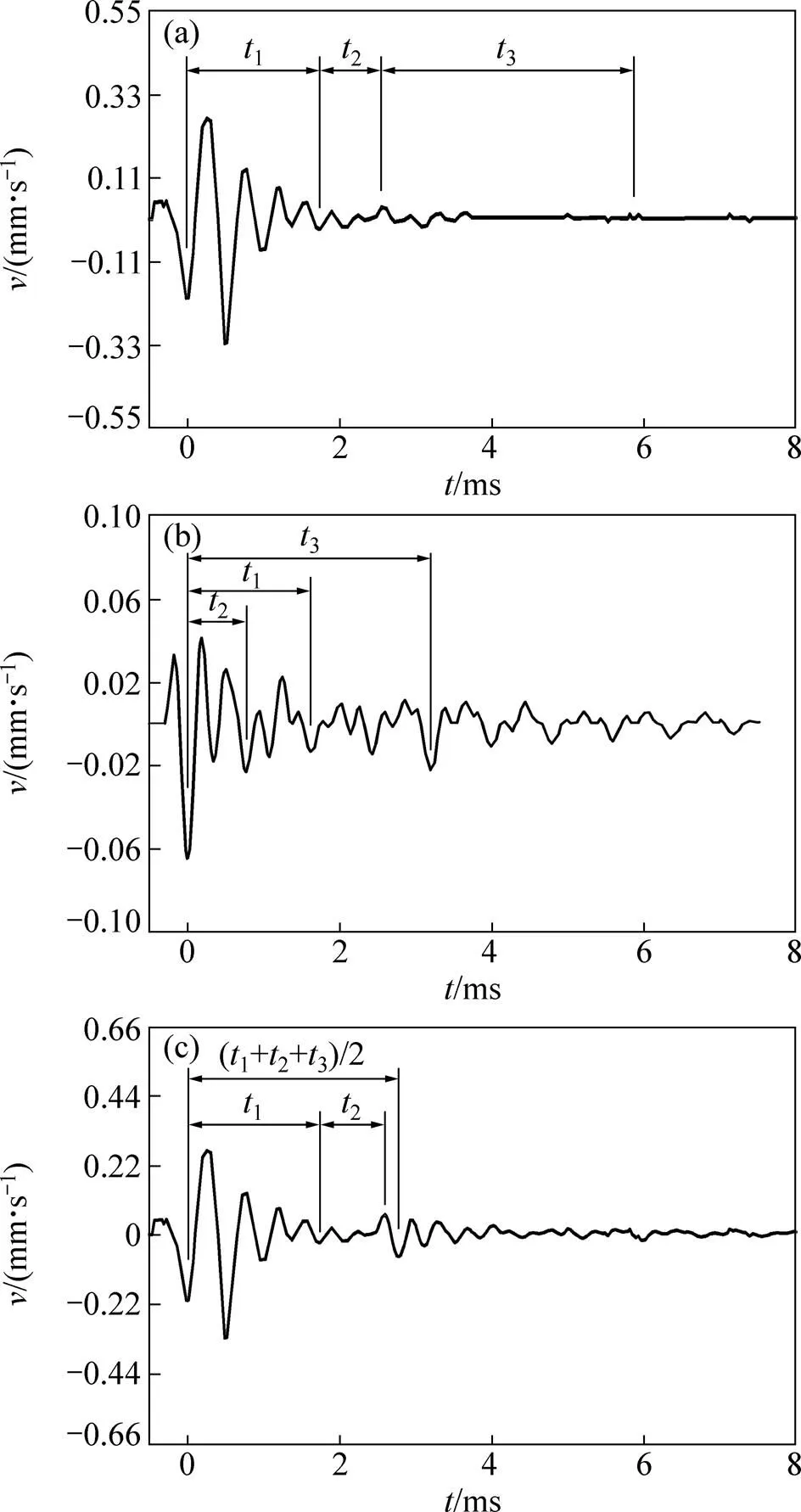
(a) 锚索端头激发方式；(b) 锚索底端激发方式；(c) 锚索端头和底端同时激发方式

图7 存在缺陷段全长注浆型锚固体应力波法质量检测时锚索端头应力波信号

Fig. 7 Stress wave signals on top of anchor cable as adopting stress wave method to detect anchorage quality in full-length grouting anchorage body with existence of defective segment

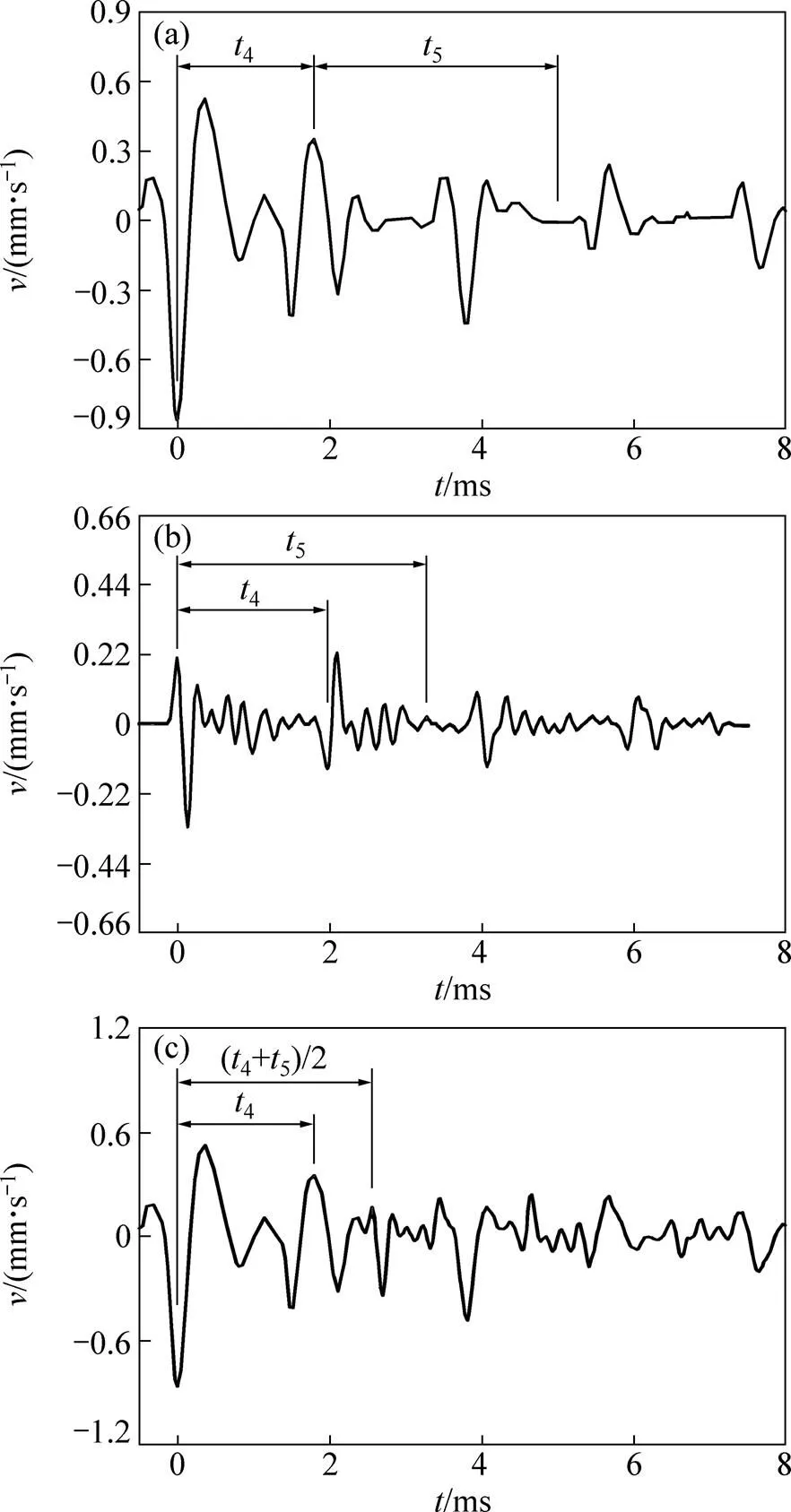
(a) 锚索端头激发方式；(b) 锚索底端激发方式；(c) 锚索端头和底端同时激发方式

图8 存在自由段非全长注浆型锚固体应力波法质量检测时锚索端头应力波信号

Fig. 8 Stress wave signals on top of anchor cable asadopting stress wave method to detect anchorage quality innon full-length grouting anchorage body withexistence of free segment

基于锚索端头接收到的应力波实测信号，并根据前述理论分析所得的各断面变化处的应力波信号与初始应力波信号的相位关系，可判别得各断面变化处对应的位置和传播时间。当各段长度为已知参数时，由应力波在各段上的传播时间计算应力波的传播速度，并与由2.2节中给定的材料参数计算得到的应力波的理论传播波速进行对比，其分析结果见表1。

表1 应力波计算参数理论结果与实测结果对比

当以2.2节所给材料参数计算得的应力波的理论传播波速为基础时，分析图6(a)和6(b)、图7(a)和7(b)、图8(a)和8(b)所得的应力波在各段上传播所需的时间，并分析锚索的长度和缺陷段位置(或各段的长度)，最后与各段的实际长度对比，其计算结果见表2。

表2 应力波法质量检测误差分析

由表1和表2可知：1) 在全长注浆型锚固体和存在自由段非全长注浆型锚固体中，对于锚索端头或底端激发方式，由锚索端头接收到的应力波信号分析和判断得到的应力波实测传播速度与理论计算速度及实测各段长度与实际各段长度均相差较小，可验证这2种激发方式对锚索锚固质量检测的可行性；2) 在存在缺陷段全长注浆型锚固体中，由于浇筑外围注浆体的尺寸和密实度没有达到设计标准，故实测值与理论计算值存在一定的差异。

从图6(a)和6(b)、图7(a)和7(b)及图8(a)和8(b)可见：虽然锚索端头激发和锚索底端激发这2种方式均可有效地对锚索的锚固质量进行分析，但在端头接收到的应力波信号存在不同程度的衰减，尤其是随着注浆段越长且越饱满时，应力波的能量衰减得越快，因而，为了能够有效地判别较长锚索的锚固质量，需要锚索端头接收到反映锚固体断面变化处的应力波信号在其传播路径上最短。将图6(a)和6(b)、图7(a)和7(b)及图8(a)和8(b)按实际情况进行线性叠加模拟，得到锚索端头和底端同时激发时锚索端头接收到的应力波信号分别如图6(c)、图7(c)和图8(c)所示。其中，应力波信号叠加的方式为：将锚索底端激发时锚索端头接收到的应力波信号(图6(b)、图7(b)和图8(b))的时间0点位置向右移动，然后与锚索端头激发时锚索端头接收到的应力波信号(图6(a)、图7(a)和图8(a))进行线性叠加。其中：为锚索端头激发时应力波在各形式锚固体中来回往返所需的传播时间。在图6(a)中，=p+2+3；在图8(a)中，=4+5，为锚索底端激发时应力波在各形式锚固体中来回往返所需的传播时间；在图6(b)中，=0；在图7(b)中，=1+2+3；在图8(b)中，=4+5。

由图6(c)，7(c)和8(c)可知：1) 锚索端头和底端同时激发方式同样能够对锚索的锚固质量进行有效判别，且其在锚索端头获得关于锚固体断面变化处信息的应力波信号传播时间是锚索端头激发和锚索底端激发产生同样效果时这两者所需的最短时间，因而，锚索端头和底端同时激发方式结合了锚索端头激发和锚索底端激发方式这两者的优点；2) 由于试验中采用人工小锤敲击方式产生应力波，故锚索端头或锚索底端传播过来的应力波信号难以区分，且存在其他杂波的影响，因此，建议在实际检测过程中选择单一的自动激发方式，且对锚索端头和锚索底端分别采用不同的应力波频率，以便区分这2种不同信号。

4 结论

1) 采用应力波法可以较准确地对锚索的长度和缺陷段的位置进行识别。

2) 采用锚索端头和底端同时激发应力波信号方式结合了锚索端头和底端分别激发应力波信号这2种方式的优点，且能够较可靠地对较长锚索的锚固质量进行有效检测。

3) 为了能够提高锚索端头和底端同时激发应力波信号方式对锚索锚固质量的有效分析能力，建议锚索端头和底端分别采用不同频率的应力波信号，以便对这2种应力波信号加以区分。

[1] MEHMET Y K, CEM K, AHMET T A, et al. Anchor application in Karatepe andesite rock slope, Izmir—Türkiye[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 245−258.

[2] 邓东平, 李亮. 边坡稳定性分析的斜条分法[J]. 中南大学学报(自然科学版), 2013, 44(8): 3351−3362.
DENG Dongping, LI Liang. Oblique slice method of slope stability analysis[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3351−3362.

[3] CHENG Jiulong, SUN Xiaoyun, FENG Li, et al. Experimental study on non-destructive testing of rock bolts based on pseudo-random signal[J]. Safety Science, 2012, 50(4): 783−786.

[4] WANG Chen, HE Wen, NING Jiangguo, et al. Propagation properties of guided wave in the anchorage structure of rock bolts[J]. Journal of Applied Geophysics, 2009, 69(3): 131−139.

[5] ZHANG C S, ZOU D H, MADENGA V. Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh density and wave frequency[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 634−639.

[6] WU Rui, XU Jinhai, LI Chong, et al. Stress wave propagation in supporting bolts:a test for bolt support quality[J]. International Journal of Mining Science and Technology, 2012, 22(4): 567−571.

[7] 汪明武, 王鹤龄. 锚固质量的无损检测技术[J]. 岩石力学与工程学报, 2002, 21(1): 126−129.
WANG Mingwu, WANG Heling. Nondestructive testing of anchoring quality[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(1): 126−129.

[8] 肖国强, 吴基昌, 周黎明, 等. 锚杆质量无损检测中的缺陷信息提取方法研究[J]. 长江科学院院报, 2012, 29(11): 73−76.
XIAO Guoqiang, WU Jichang, ZHOU Liming, et al. Method of extracting defective information in non-destructive detection of anchor quality[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(11): 73−76.

[9] 张昌锁, 李义, 赵阳升, 等. 锚杆锚固质量无损检测中的激发波研究[J]. 岩石力学与工程学报, 2006, 25(6): 1240−1245.
ZHANG Changsuo, LI Yi, ZHAO Yangsheng, et al. Study on optimum excitation wave in grout quality nondestructive testing of rock bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1240−1245.

[10] 黄理兴. 岩石动力学研究成就与趋势[J]. 岩土力学, 2011, 32(10): 2889−2900.
HUANG Lixing. Development and new achievements of rock dynamics in China[J]. Rock and Soil Mechanics, 2011, 32(10): 2889−2900.

[11] 习小华. 锚杆锚固质量动力响应特征与检测技术研究[D]. 西安: 西安科技大学建筑与土木工程学院, 2013: 1−10.
XI Xiaohua. Study on bolt anchoring quality dynamic response character and testing technology[D]. Xi’an: Xi’an University of Science and Technology. College of Architecture and Civil Engineering, 2013: 1−10.

[12] 李新平, 江杰, 鲁志鹏, 等. 应力波法锚杆加固无损检测的数值模拟分析研究[J]. 岩石力学与工程学报, 2005, 24(增1): 4647−4652.
LI Xinping, JIANG Jie, LU Zhipeng, et al. Numerical simulation analysis of nondestructive detection of stress wave in anchorage bolts[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S1): 4647−4652.

[13] 马宏伟, 吴斌. 弹性动力学及其数值方法[M]. 北京: 中国建材工业出版社, 2000: 12−36.
MA Hongwei, WU Bin. Elastic dynamics and its numerical method[M]. Beijing: China Building Materials Industry Press, 2000: 12−36.

[14] 张东方. 锚杆锚固质量动力无损检测数值模拟研究[D]. 郑州: 郑州大学水利与环境工程学院, 2010: 21−54.
ZHANG Dongfang. The numerical simulation study on dynamic nondestructive detection in anchorage quality of rock bolts[D]. Zhengzhou: Zhengzhou Univercity. College of Water Conservancy and Environment, 2010: 21−54.

[15] 吕丹丹. 低频信号的锚杆动态响应特征研究[D]. 石家庄: 河北科技大电气信息学院, 2011: 7−26.
LÜ Dandan. Study on the low frequency signal anchor bolt of dynamic response charateristics[D]. Shijiazhuang: Hebei University of Science and Technology. College of Electric Machines and Electronic, 2011: 7−26.

[16] 梁龙龙. 应力波法在边坡预应力锚索(无黏结型)结构检测中的试验研究[D]. 北京: 铁道科学研究院, 2007: 25−61.
LIANG Longlong. A study on stress wave method in pre-stressed (non-bonded) anchor cable structure detection of slope[D]. Beijing: Academy of Railway Sciences, 2007: 25−61.

(编辑 陈灿华)

Experimental study on stress wave method fordetecting anchorage quality of anchor cable

DENG Dongping, LI Liang, GAO Liansheng

(School of Civil Engineering, Central South University, Changsha 410075, China)

The stress wave method is difficult to be applied to obtain effective stress wave signal that reflects the section change of anchorage body in the long anchor cable. Based on the actual models of anchorage body with three special types, i.e. full-length grouting anchorage body, full-length grouting anchorage body with existence of defective segment, and non full-length grouting anchorage body with existence of free segment, and using two stress wave excitation modes, i.e. stress wave signal exciting respectively on top or bottom of anchor cable, the reliability of stress wave method to detect anchorage quality was verified through comparing the theoretical vibration velocity of the stress wave with the measured ones. Then, by combining the above two stress wave excitation modes, the feasibility of stress wave signal exciting simultaneously on top and bottom of anchor cable to detect anchorage quality of anchor cable was studied. The results show that the excitation mode of stress wave signal simultaneously on top and bottom of anchor cable can effectively detect anchorage quality of anchor cable, and signal received on top of anchor cable in this mode is the stress wave signal with the shortest propagation path for reflecting change positions of anchorage body sections. Meanwhile, the two kinds of stress wave signals are suggested to adopt different frequencies to distinguish stress wave signals exciting respectively on top and bottom of anchor cable.

anchor cable; anchorage quality; stress wave; excitation mode; propagation velocity; feature line method

10.11817/j.issn.1672-7207.2016.08.031

TU45

A

1672−7207(2016)08−2768−08

2015−09−03；

2015−10−27

中国博士后科学基金面上资助项目(2015M580702)；中南大学博士后科学基金资助项目(201508)；贵州省交通运输厅科技项目(2014122066)(Project (2015M580702) supported by the Postdoctoral Science Foundation of China; Project (201508) supported by the Postdoctoral Science Foundation of Central South University; Project (2014122066) supported by Department of Transportation Foundation of Guizhou Province)

邓东平，博士(后)，从事道路与铁道工程等研究；E-mail：dengdp851112@126.com