一类冠图的2种度结合边重构数

黄陈辰，　马美杰

(浙江师范大学 数理与信息工程学院,浙江 金华　321004)



一类冠图的2种度结合边重构数

黄陈辰，马美杰

(浙江师范大学 数理与信息工程学院,浙江 金华321004)

根据冠图Pn5Cm的结构特点,通过分析Pn5Cm的一个度结合边主子图可能重构的图的结构,确定了它的2种度结合边重构数,推广了关于路与圈的冠图的相关结论.

冠图;边主子图;边重构数;度结合边重构数

0　引　言

图的重构猜想最早是由Ulam[1]和Kelly[2-3]提出的.对于图G,把删除图的一个顶点u及与该顶点关联的边后得到的子图称为主子图,记为G-u.由图的所有主子图组成的多重集合称为主子图集.图的重构猜想是指每个至少有3个顶点的图都能唯一地被它的主子图集所确定.其后,Harary[4]提出了边重构猜想,即至少含有4条边的图能够被它的边主子图集所决定,其中,边主子图是指在图G中删除一条边e后得到的子图,记为G-e.本文主要考虑度结合边主子图的重构问题.用d(v)表示图G中顶点v的度,对图G的边e=uv,其边度为d(e)=d(u)+d(v)-2.图的度结合边主子图由边主子图和删除边的边度组成,记为(G-e,d(e)).度结合边重构数是指能重构图G所需的度结合边主子图的最少个数,记为dern(G).一致度结合边重构数是指任意k个度结合边主子图都能重构图G的最小整数k,记为adern(G).

关于图的重构已经有了一些结论.1995年,刘富贵[5]证明了关于重构猜想的部分结果;2003年,刘桂真等[6]给出了两类图同构的充分必要条件;2007年,谢力同等[7]讨论了连通图的可重构性;2012年,Monikandan等[8]确定了当图G为正则图、完全二部图、路、轮图、双星图或平衡三部图时,dern(G)和adern(G)的值.

G1和G2的冠图,是指G1的一个拷贝和G2的|V(G1)|个拷贝,且G1的第i个顶点与G2的第i个拷贝的每个顶点均相连,记为G15G2.2013年,Monikandan等[9]确定了Cn5Km和Pn5K1的2种度结合边重构数;2015年,石黄萍等[10]给出了冠图P25Cm的2种度结合边重构数.

记Δ(G)为G的最大度,δ(G)为G的最小度;用Pn(n≥1)表示n阶路;Cm(m≥3)表示m阶圈;Kn(n≥1)表示n阶完全图.轮图是指在一个n-1(n≥4)阶圈中加一个点,使得该点与圈上的每个点均有边相连,记为Wn(n≥4).记Pn5Cm(n≥1,m≥3)表示Pn和Cm的冠图.由冠图的定义知,δ(Pn5Cm)=3,P15Cm≅Wm+1.

1　预备知识

引理1[8]若Wn是n(n≥4)阶的轮图,则dern(Wn)=1,且

引理2[10]令G=P25Cm.若m≥3,则

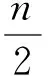
引理3[10]若图G有一条边e满足:d(e)=0或者在G-e中除边e的端点之外的任意2个不相邻点的度和不等于d(e),则度结合边主子图(G-e,d(e))可重构图G.

引理4令G=Pn5Cm(n≥1,m≥3),则G中的度结合圈边主子图(G-e,4)可重构图G.

证明在G中取Cm中的一条边e,其度结合边主子图为(G-e,4).在G-e中,由m≥3知,除边e的2个端点外,任意2个不相邻点的度和至少为5.由引理3知,(G-e,4)可重构图G.引理4证毕.

引理5令G=Pn5Cm(n≥4,m≥3),则G的2个不同的度结合路边主子图可重构图G.

证明设图G的2个度结合路边主子图为(G-hk,2m+2)和(G-hl,d(hl)).图H′表示在边主子图G-hk中添加一条2m+2度边e′后得到的图.当n=4时,边主子图G-hk中恰有4个最大度为m+1的点,连接任2个不相邻的m+1度点后得到的图H′，都有H′≅G.下设n≥5.

1)边e′的2个端点的点度都是m+1.

若H′G,则边e′的2个端点在G-hk的同一分支中,且边e′在图H′的一个圈C上.圈C上的边度都是2m+2,且删除圈C上任一条边后得到的边主子图与G-hk同构.

当n=5时,图H′的不在圈C上的边度都小于2m+1,故图H′的度结合边主子图集不含(G-hl,d(hl)).

当n≥6时,在图H′中删除不在圈C上的2m+2或2m+1度边后得到的边主子图有3个连通分支,而G-hl只有2个连通分支,故图H′的边主子图集不含G-hl.

2)边e′的2个端点的点度不同,即m=3,d(e′)=8且边e′的2个端点u和v在G-hk中的点度分别为3和5,因此dH′(v)=6.因为Δ(G)=5,所以图H′中不与点v关联边的边主子图不在图G的边主子图集中.图H′中与点v关联的7度边e"的另一端点的点度为3,边主子图H′-e"的最小度为2,而图G的7度边的边主子图的最小度为3,故图H′的边主子图集不含G-h1.若图H′中除边e′外,与点v关联边的边度都不等于8,则图H′的边主子图集不含G-hl;若图H′中除边e′外,与点v关联边h′的边度为8,则点v是图G的边h1的端点;若边e′的另一端点u与h1的异于v的端点相邻,则H′-h′≅G-hk.否则,边主子图H′-h′有个K4分支,而G-hl(l≠1)没有此分支,所以图H′的边主子图集不含G-hl.

综上即可得引理5的结论.证毕.

引理6令G=Pn5Cm(n≥2,m≥3),则G的一个度结合路边主子图和一个度结合交叉边主子图可重构图G.

证明设图G的一个度结合路边主子图为(G-hk,d(hk)),另一个度结合交叉边主子图为(G-ei,d(ei)).图H′表示在边主子图G-hk中添加一条d(hk)度边e′后得到的图.若边e′的2个端点在G-hk的同一分支中,则图H′含有2个连通分支,而边主子图G-ei都是连通图.所以,图H′的边主子图集不含G-ei.下设边e′的2个端点为u和v，并使u和v在G-hk的不同分支中.若边e′的一个端点u在G-hk中的点度为m+2,则dH′(u)=m+3.因为Δ(G)=m+2,所以图H′中不与点u相关联的边的边主子图不在图G的边主子图集中.在H′中与点u相关联的边的边度至少为m+4,而ei的边度至多为m+3,所以图H′的边主子图集不含G-ei.因此,边e′的端点在G-hk中的点度至多为m+1.

当d(hk)=2m+2时,边e′的2个端点在G-hk中的点度均为m+1,则H′≅G.

当d(hk)=2m+1时,边hk为h1,边e′的2个端点在G-h1中的点度分别为m和m+1,则H′≅G.

当d(hk)=2m时,n=2且只有一条路边.当m=3时,G-hk中所有的顶点都是3度点,任意连接2个不相邻的3度点后得到图H′,有H′≅G;当m≥4时,G-hk中除边hk的2个端点外,任何2个不相邻点的度和不等于2m.由引理3知,(G-hk,2m)可重构图G.

引理6证毕.

引理7令G=Pn5Cm(n≥3,m≥3),则G的2个度结合交叉边主子图可重构图G.

证明设G的2个度结合交叉边主子图为(G-ei,d(ei))和(G-ej,d(ej)),且d(ei)≥d(ej).图H′表示在边主子图G-ei中添加一条d(ei)度边e′后得到的图.

1)d(ei)=m+3.若H′G,且e′的2个端点在图G-ei的度分别为为m+1和2,则H′至多有n-2条割边.在H′中删除m+3或m+2度边e"后得到的边主子图H′-e"仍至多有n-2条割边,而G-ej有n-1条割边.因此,图H′的边主子图集不含G-ej.

若H′G,且e′的2个端点在图G-ei的度均为3,则m=3且e′的2个端点在图G-ei的不同圈C3中.设e′的2个端点如图1所示.图H′中有n-2条割边.在H′中删除6度边e"后得到的图H′-e"有n-1条割边,但此时H′-e"的直径为n+2,而G-ej的直径为n+1.否则,在H′中删除不同于e′的5或6度边后得到的边主子图至多有n-2条割边,而G-ej有n-1条割边.因此,图H′的边主子图集不含G-ej.

图1　边e′的2个端点均为3度点的重构图H′(H′G)

2)d(ei)=m+2,即2个度结合交叉边主子图都为(G-e1,m+2).当m≥5时,由m+2≥7和引理3知,H′≅G.下设3≤m≤4.若H′G且e′的2个端点在图G-e1的不同圈Cm中,则H′至多有n-2条割边.从H′中删除m+2度边e"后H′-e"仍至多有n-2条割边,而G-e1有n-1条割边,故图H′的边主子图集不含2个G-e1.

若H′G且e′的2个端点在图G-e1的同一圈Cm中,则m=4且H′有3个4度点.而G-e1只有1个4度点.故删除的6度边e"的2个端点都为4度点,即只需考虑e′的端点在图G的同一C4圈中且e1的一个端点在该圈上的情况.删去e"后,在H′-e"中无4度点与6度点相邻,而在G-e1中有1个4度点与6度点相邻.故图H′的边主子图集不含2个G-e1.

综上即可得引理7的结论.证毕.

2　主要结果

根据引理4的证明,可得如下定理:

定理1令G=Pn5Cm(n≥1,m≥3),则dern(G)=1.

定理2令G=Pn5Cm.若n≥1和m≥3,则

证明当n∈{1,2}时,由引理1和引理2可知结论成立.下设n≥3.由引理4～引理7知,图G的任意3个度结合边主子图集S可重构图G,所以adern(G)≤3.

当n∈{3,4},m≥4时,图G的任意2个度结合边主子图集可重构图G.由引理4～引理7知,只需证明图G的2个度结合边主子图(G-h1,2m+1)可重构图G.图H′表示在边主子图G-h1中添加一条2m+1度边e′后得到的图.当m≥5或m=4,n=3时,边e′的端点是G-h1中2个不相邻的m和m+1度点,有H′≅G.当m=4,n=4时,若H′G,则此时Δ(H′)=7,不妨设d(v)=Δ(H′)=7.由于Δ(G)=6,且在H′中与顶点v相关联的边中只有一条为2m+1度边,所以图H′的边主子图集不含2个度结合边主子图(G-h1,2m+1).因此,adern(G)≤2.

下面证明下界.

1)m=3.当n=3时,图2所示的图与P35Cm有2个公共的度结合边主子图(G-h1,7),所以,adern(G)≥3.当n=4时,图3所示的图与P45Cm有2个公共的度结合边主子图(G-h1,7),所以,adern(G)≥3.

n=3　　　　　　　　　　　　　　　　　　　　　　　n=4图2　含2个(G-h1,7)的重构图H′(H′G)　　　图3　含2个(G-h1,7)的重构图H′(H′G)

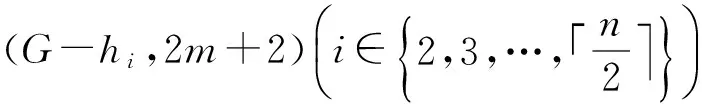
2)当n∈{3,4},m≥4时,图5所示的图与图G有1个公共的度结合边主子图(G-e2,m+3),所以,adern(G)≥2.

综上,即可得定理2的结论.证毕.

图4　含2个(G-hi,2m+2)的重构图H′(H′G)

图5　含1个(G-e2,m+3)的重构图H′(H′G)

3　结　语

本文通过分析冠图Pn5Cm的结构特点,寻找一个图,使其与冠图有尽可能多的公共的度结合边主子图,从而确定它的下界,由下界猜测其上界,并加以证明,确定了冠图Pn5Cm的2种度结合边重构数.结合其他学者已经得到的关于冠图的度结合边重构数的结论,还可以考虑关于冠图G=Cn5Pm与G=Pn5Pm的2种度结合边重构数.

[1]UlamSM.Acollectionofmathematicalproblems[M].NewYork:IntersciencePublishers,1960:20.

[2]KellyPJ.Onisometrictransformations[D].Wisconsin:UniversityofWisconsin-Madison,1942.

[3]KellyPJ.Acongruencetheoremfortrees[J].PacificJMath,1957,7(1):961-968.

[4]HararyF.Onthereconstructionofagraphfromacollectionofsubgraphs[C]//FielderM.Theoryofgraphsanditsapplications.NewYork:AcademicPress,1964:47-52.

[5]刘富贵.关于重构猜想的部分结果[J].武汉交通科技大学学报,1995,19(1):66-68.

[6]刘桂真,禹继国,谢力同.两类图同构的充分必要条件[J].山东大学学报:自然科学版,2003,38(3):1-4.

[7]谢力同,刘家壮.论连通图的可重构性[J].经济数学,2007,24(3):221-223.

[8]MonikandanS,RajSS.Degreeassociatededgereconstructionnumber[J].CombinatorialAlgorithms,2012,7643(3):100-109.

[9]MonikandanS,AnushaDP,SundarRS.Degreeassociatededgereconstructionnumberofgraphs[J].JDiscreteAlgorithms,2013,23(1):35-41.

[10]石黄萍,马美杰.冠图P25Cm的2种度结合边重构数[J].浙江师范大学学报:自然科学版,2015,38(2):176-178.

(责任编辑陶立方)

Two degree associated edge reconstruction numbers of a kind of corona graph

HUANG Chenchen,MA Meijie

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

Based on the structure property of the corona graphPn5Cm, it was determined the two degree associated edge reconstruction numbers ofPn5Cmby considering the possible reconstructions from a degree-associate edge-card. The results extended some relevant results about the corona graph of path and cycle.

corona graph; edge-card; edge reconstruction number; degree-associate edge reconstruction number

10.16218/j.issn.1001-5051.2016.03.005

收文日期：2015-10-17；2015-12-11

黄陈辰(1990-),女,浙江海宁人,硕士研究生.研究方向:图论.

马美杰.E-mail: mameij@zjnu.cn

O157.5

A

1001-5051(2016)03-0263-05