巧用轨迹方程求解平抛问题

◇　陕西　王永利



巧用轨迹方程求解平抛问题

◇陕西王永利

平抛运动的轨迹方程是半支开口向下的抛物线．物理上处理平抛运动的基本方法是将其分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动．实际上,许多平抛运动的问题借助运动轨迹方程转化为数学问题更容易求解．

1　平抛运动的轨迹方程

2　轨迹方程在解题中的应用

利用得到的轨迹方程,我们可以将许多平抛运动的问题转化为数学问题轻松求解．下面举2个实例．

图1　　　　　　　　　　　图2

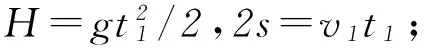
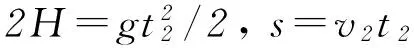
因为A处抛出的物体擦过屏M的顶端,所以

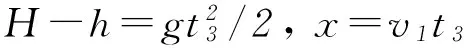
同理,B处抛出的物体也擦过屏M的顶端,有

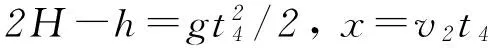
联立解得

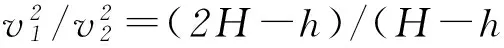
所以有

(2H-h)/(H-h)=8，

解得h=6H/7，即屏幕的高度h=6H/7.

方法2建立直角坐标系如图2所示,使物体从A、B2点抛出后的运动轨迹都是顶点在y轴上的抛物线．设2个抛物线方程分别为y=-aAx2+H和y=-aBx2+2H. 把E(2s,0)、F(s,0) 2点分别代入2个方程求解系数得aA=H/4s2,aB=2H/s2，由此确定2个平抛运动的轨迹方程为

由方程组解得纵坐标y=6H/7，即为屏的高度．

图3

(1) 设击球点在3m线正上方高度为2.5m处,试问击球的速度在什么围内才能使球既不触网也不过界.

(2) 若击球点在3m线正上方的高度小于某个值,那么无论水平击球的速度多大,球不是触网就是越界,试求这个高度(g取10 m·s-2).

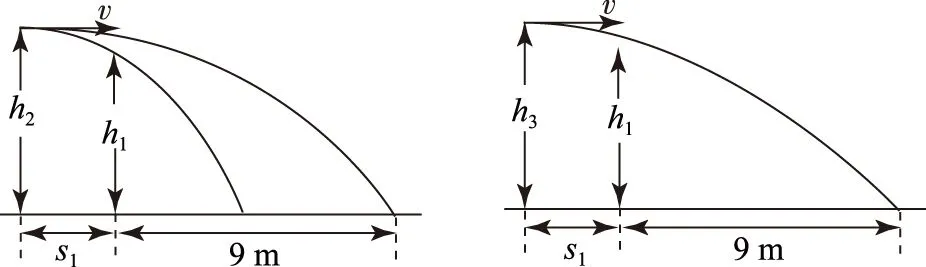
图4　　　　　　　　　　图5

(2) 如图5所示,设击球点高度为h3时,球恰好既触网又压线．根据平抛运动规律，球触网则有

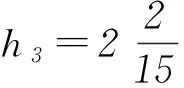
图6　　　　　　　　　　图7

3　小结

高考大纲明确地把“利用数学方法解决物理问题”作为物理学科考查的5大能力之一,这是由物理学作为一门精确科学与数学之间密不可分的关系决定的,也是我们实施素质教育,培养创新型人才的要求．物理教师在平时的教学中应该加强这方面的引导,多给学生渗透函数与方程、数形结合、极限等数学思想．指导学生在处理物理问题时灵活应用这些数学方法,以适应素质教育的要求．

陕西省乾县第一中学)