由图象特征破解一类三角求值问题

◇　山东　王殿刚



由图象特征破解一类三角求值问题

◇山东王殿刚

函数y=Asin(ωx+φ)的图象和性质是高考重要考查内容.其中根据φ、ω、Α对函数图象、性质的影响,给出部分性质或图象特征来确定φ、ω、Α的值或范围是高考的常考题型．利用图象特征结合特殊与一般、转化与化归等思想方法的综合运用是成功解答此类问题的关键．

A11;B9;C7;D5

下面就此问题进行变式拓展,通过归纳题型、总结方法,帮助同学们提高解决问题的能力．

1　给出对称中心及对称轴

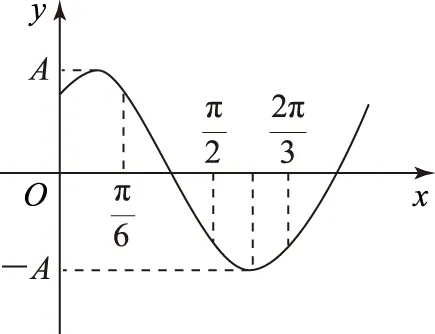
图1

2　给出2个相邻的极值点

3　给出对称中心及最值点

4　给出图象及最值点

图2

A1;B2;

C3;D4

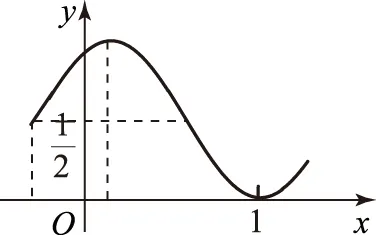
图3

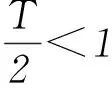
又ω为整数,所以选项为B．

以上给出的数例形式多变,但万变不离其宗．求解时只要准确把握φ、ω、Α对函数y=Asin(ωx+φ)图象、性质的影响,就可锁定目标函数图形,从而将问题解决．

山东省枣庄市枣庄八中南校)