YN38CRD型柴油机机体试验模态分析*

古元峰　王贵勇　黄　冈　毕玉华　申立中

（昆明理工大学云南省内燃机重点实验室云南昆明650500）

YN38CRD型柴油机机体试验模态分析*

古元峰王贵勇黄冈毕玉华申立中

（昆明理工大学云南省内燃机重点实验室云南昆明650500）

机体有限元模型是进行柴油机振动计算和噪声预测的主要工具，而试验模态分析是对有限元模型进行验证、修正和补充的重要方法。使用多项式拟合法和最小二乘复频域法进行YN38CRD型柴油机机体的试验模态分析，结合有限元法的理论模态参数，对三种方法的结果进行了比对和分析，且通过模态置信准则验证了模态参数。结果表明，试验模态参数与理论模态参数吻合度较高，相互验证了试验和有限元数学模型的正确性。振型比对发现，机体振动最大变形位置多集中于曲轴箱，缸孔的椭圆振动会引起气缸漏气和窜机油。研究结果为优化柴油机振声性能奠定了基础。

机体试验模态分析多项式拟合法最小二乘复频域法模态置信准则

引言

汽车噪声法规的日趋严格和消费者对汽车舒适性的需求提高，推动了减振降噪技术在汽车领域的深入研究及广泛应用。柴油汽车在欧洲已得到普及，但柴油机NVH性能直接或间接影响着汽车NVH品质，成为决定汽车市场认可度的重要因子［1］。机体是发动机整机的骨架，是其他零部件直接或间接安装的基体，也是诱发气缸盖、油底壳等零部件振声问题的激励源［2-3］。随着柴油机设计朝着轻量化、高速化、大功率化及低排放迈进，机体不仅要有足够的几何精度和均匀的材料分布，而且应具备良好的刚度、强度和动态特性［4］。进行机体模态分析成为柴油机开发或改进中一项重要内容，试验法与有限元法相结合已成为分析柴油机模态特性的主要方法［5］。

本文对YN38CRD型柴油机机体进行自由状态下的试验和理论模态分析。试验模态分析采用基于LabVIEW软件开发的以多项式拟合法和最小二乘复频域法为核心的ModalVIEW软件进行。结合有限元法的理论模态参数，对结果进行比对和分析，并基于模态置信准则对模态识别结果进行合理性分析。

1　试验模态分析理论

试验模态分析是通过试验测得激励和响应的时间历程，进行数字信号处理，获得频响函数（FRF），选择模态参数识别方法解得系统模态参数（频率、阻尼和振型）。对于机体的结构振动问题可简化为n自由度的线性时不变振动系统，建立以质量、阻尼、刚度为参数的关于位移的振动微分矩阵方程［5-6］。

2　模态测试方案

对YN38CRD型柴油机机体进行试验模态测试时，将机体用橡皮绳悬置于行车上使其处于自由状态，用胶粘剂将加速度传感器粘接于机体的各测量节点。本文采用单点输入多点输出（SIMO）的锤击脉冲激励法，移动力锤逐点激励结构的不同自由度（节点和方向），同步采集各传感器信号，以获取频响函数矩阵的多行数据。使用基于LabVIEW开发的模态测试分析系统ModalVIEW对每激励点进行4次激励得到的功率谱进行线性平均，再变换为频响函数形式存储。依次完成全部数据采集后，将所有分组测量数据合并，供ModalVIEW进行模态估计时调用。

2.1模态测试分析系统

模态测试分析系统由激励系统、数据采集系统和试验模态分析系统组成，如图1所示。

力锤选用带有压电石英力传感器的LC1301型力锤，其灵敏度为3.86pC/N；加速度传感器选用LC0101型内装IC压电加速度传感器，其灵敏度为100±2.58mV/g。数据采集系统选用NI公司的PXI 4498数据采集板卡和PXI 1050高端硬件平台。ModalVIEW试验模态分析软件是基于LabVIEW开发的应用软件。

2.2测点的布置

根据力锤尺寸和传感器安装位置，结合机体动态特性和测点均布的原则，通过ModalVIEW建立机体三维测试模型。激励点、响应点及插值点共216个，如图2所示。本研究在机体上布置18个单轴加速度传感器，选取20个激振点。

图1　模态测试分析系统

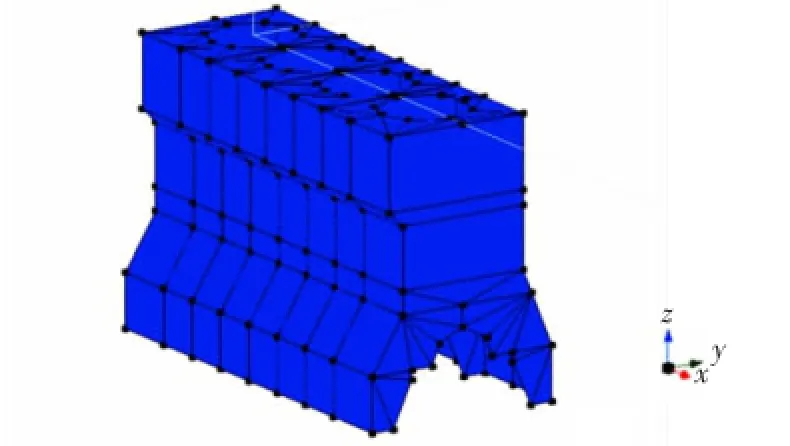
图2　三维测试模型

2.3数据采集及后处理

因外界因素的干扰和结构的非线性特点，使得试验数据可靠性不足。为使试验结果可靠，在数据采集及后处理中需采取一些必要措施：

1）试验模态分析的核心是通过频响函数来识别结构的模态参数，故频响函数精度成为直接影响模态估计结果优劣的关键。如果采样频率选择不合理，采集的时域信号经离散傅里叶变换会引起混频现象。高频频谱对机体动态设计指导意义不大，故模态分析的最高频率选为2050Hz，采样频率选为4100Hz。

2）数字信号处理以截断信号为处理对象，截断信号会增加新的频率成分，并使谱值大小发生改变。对其加窗处理，泄露情况会得到改善。加速度信号的大量重要信息集中在信号初始部分，故选择指数窗。力锤激励信号属于瞬态信号，故选择力窗。

3）试验模态分析的数学模型是建立在振动系统的可控性和可观性假设基础之上的，故中小型结构和模态不密集结构的试验模态分析，采用单点激励就可获得满意结果。冲击力锤设备简单、价格低廉，且对工作环境适应性较强，特别适合于现场测试。机体的结构适中，阻尼较低，故采用锤击脉冲激励法。

4）对采集的时域信号进行离散傅里叶变换求得的频响函数并不光滑，是因为信号中混有大量随机噪声。对每个激振点进行多次激励，待数据采集完成后，通过对得到的功率谱进行平均，再进一步估算频响函数、相干函数等其他谱函数，可以降低噪声的影响。对每激励点进行4次激励，同一激振点各组数据地位相等，故采用频域平均中的线性平均技术。

2.4模态分析数据采集

为了解激励与其响应的线性相关度，故引入相干函数进行评价，表达式为

式中，GFF为激励的自功率谱密度；GXX为响应的自功率谱密度；GFX为激励与响应的互功率谱密度。

图3所示为激励与响应的相干系数。其相干系数主要分布在0.85以上，表明所测数据可信度较高。

图3　各测点相干信号曲线

根据上述试验方案，进行YN38CRD型柴油机机体试验模态分析的数据采集。共360组线性平均后的频响函数，如图4所示，横坐标为频率，纵坐标为频响函数的对数幅值。

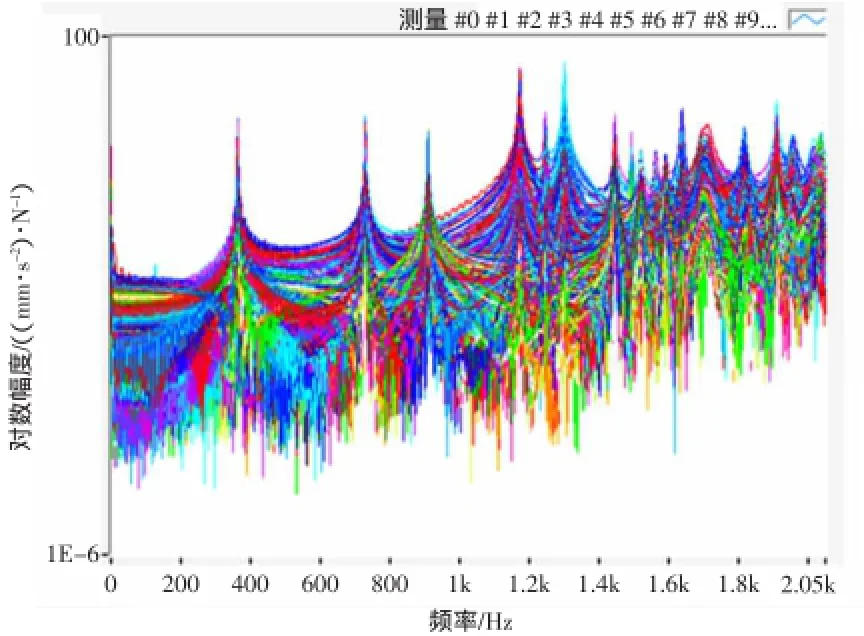
图4　各测点频响函数幅值曲线

3　模态参数识别的频域方法

振动结构的参数识别有物理参数识别、模态参数识别及非参数识别。模态参数识别为模态分析中最为基本和重要的参数识别类型。曲线拟合为现代意义的模态参数识别法，是建立在最优控制原则上，按照最优控制准则和算法用理论曲线拟合实测曲线，并使误差最小，从而得到反映系统特性的最优数学模型。

3.1多项式拟合法

用多项式拟合法（Levy法）做参数识别的数学模型时，采用有理分式函数作频响函数［7］。由于频响函数未做模态展开式的简化，理论模型是精确的，因而具有较高的参数识别精度。

利用多项式拟合法对所测的360组频响函数进行300～1 700 Hz频率范围内的试验模态分析，得到如图5所示的部分拟合频响曲线，红色曲线为拟合频响函数，蓝色曲线为测量频响曲线。两曲线吻合度较高，表明多项式拟合法的模态参数识别精度高。

图5　Levy法的测量和拟合频谱

3.2最小二乘复频域法

将机体的频响函数化简为m维输入l维输出的线性多自由度系统［8-10］。

利用最小二乘复频域法（LSCF）对所测的360组频响函数进行300～1 700 Hz频率范围内的试验模态分析。首先得到如图6所示的稳态图，横坐标为频率，纵坐标为阶次。进而在稳定图中选择纵向比较一致的‘S’对应的频率作为模态频率，再根据选定模态频率完成频响曲线拟合，如图7所示。拟合频响函数曲线与测量频响函数曲线的吻合度较高，表明最小二乘复频域法能较好地识别结构模态参数。

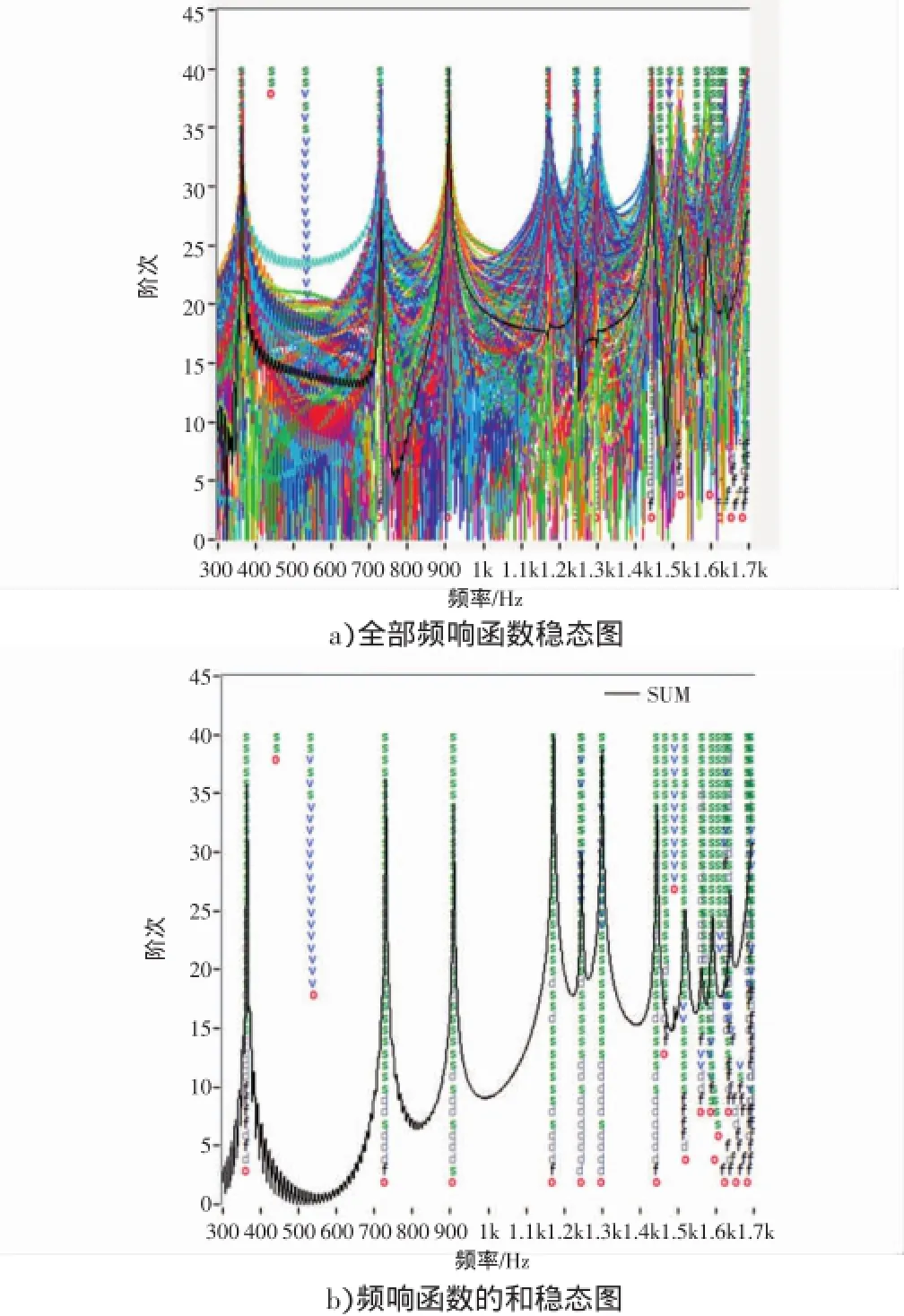
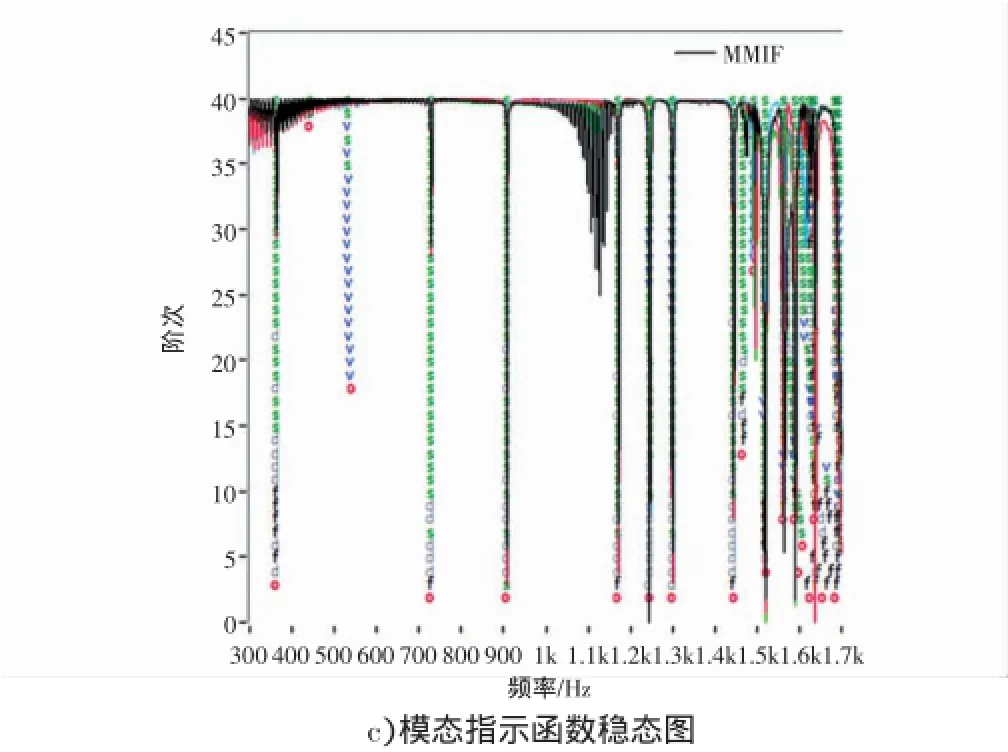
图6　稳态图

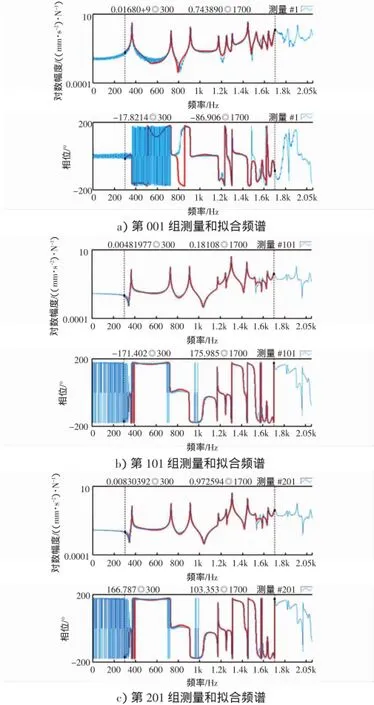
图7　LSCF的测量和拟合频谱

4　试验与理论结果比对

4.1机体有限元自由模态计算

有限元模态数值模拟过程中，选择Hypermesh软件作前处理器，ABAQUS软件作求解器。YN38CRD型柴油机机体由灰铸铁HT250铸造而成［11］。有限元模型采用二阶四面体修正单元进行网格划分，共有节点数1 109 331个，单元数638 050个，如图8所示。

图8　YN38CRD型柴油机机体有限元模型

4.2试验与理论结果比较

通过试验模态分析与有限元模态分析，分别得到机体的各阶固有频率及主振型。动力学分析主要考虑系统的低阶固有频率，且高频模态振型较为复杂，故比对前8阶的自由模态的主振型，如表1所示。前10阶的自由模态参数比对，如表2所示。

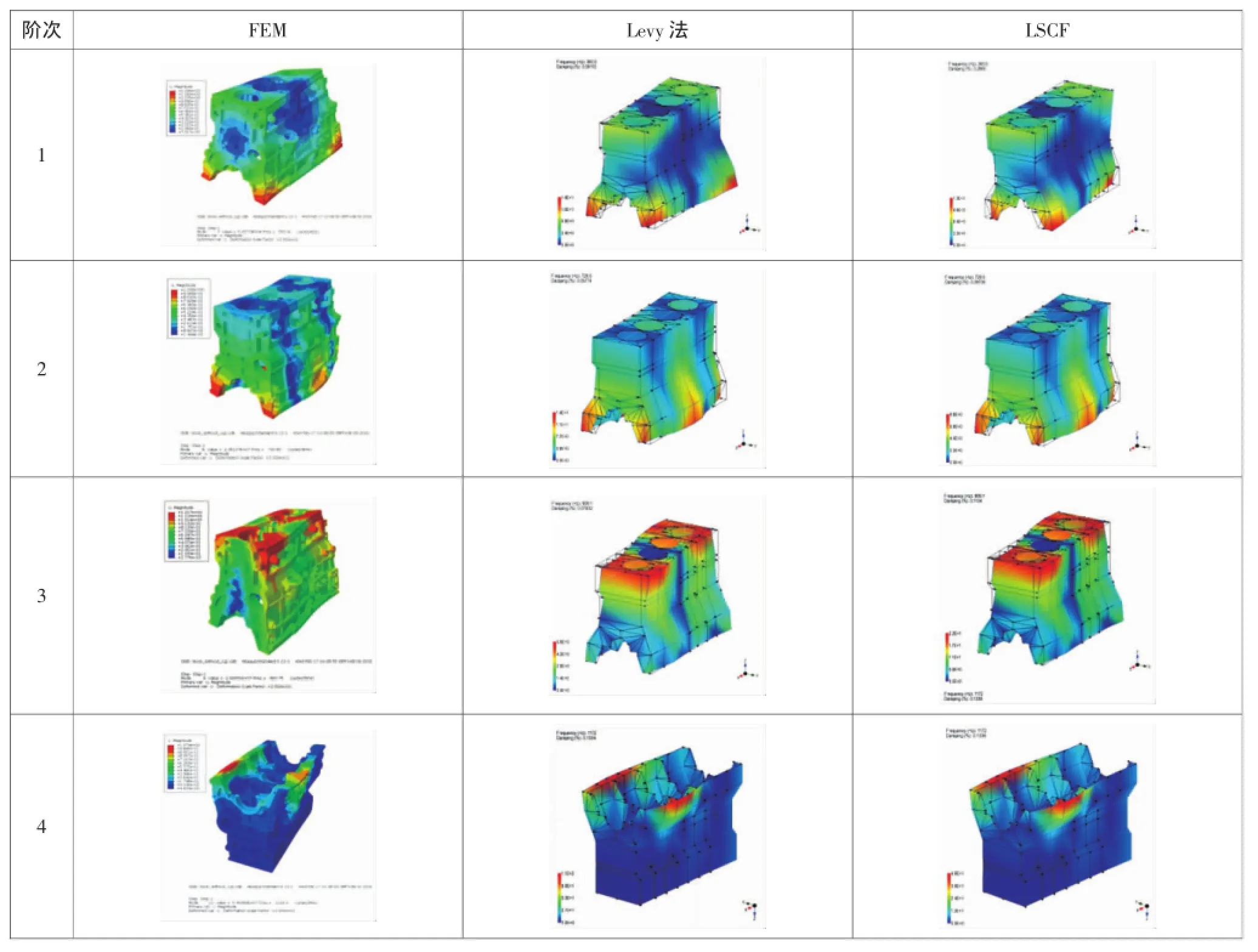
表1　试验模态振型与理论模态振型比对

续表1试验模态振型与理论模态振型比对

表2　机体试验法与有限元法的模态参数比对

机体前10阶固有频率范围为359～1 652 Hz。试验模态分析的Levy法和LSCF的振型、频率几乎相同，阻尼相差明显，但阻尼变化趋势一致，表明这两种数学模型都有良好的精度。试验法和有限元法的前8阶模态振型基本一致，各阶固有频率误差较小，第3阶固有频率误差最大，为5.4%，其余各阶误差都小于2%。故相互验证了此两种试验模型和理论模型的正确性。

分析发现，机体振动最大变形位置多集中于曲轴箱，在前8阶模态范围内的振动主要由扭转振动和弯曲振动构成，也成为机体振动和噪声辐射强烈的主要原因。与机体曲轴箱固定连接的油底壳刚度较小，故应对机体曲轴箱进行动态特性强化，以优化整机振声性能。

分析还发现，机体气缸体的振动会使缸孔产生椭圆振动，且缸孔椭圆振动长轴与椭圆活塞长轴方向相互垂直。故缸孔的椭圆振动会影响缸套与活塞间的密封，引起气缸漏气、窜机油。

4.3试验与理论模态相关性分析

通过试验法和有限元法得到的结构模态参数，两者都可能出现虚假模态，且各有误差。模态置信准则（MAC）是检验模态结果是否合理的常用方法。通过比较不同模态向量间的线性相关度来判断各阶模态的可信度。如果模态幅值相干系数越接近1，说明两者线性相关；如果模态幅值相干系数越接近0，则说明两者线性独立。第i阶模态与第j阶模态间的模态幅值相干系数MACij的定义为：

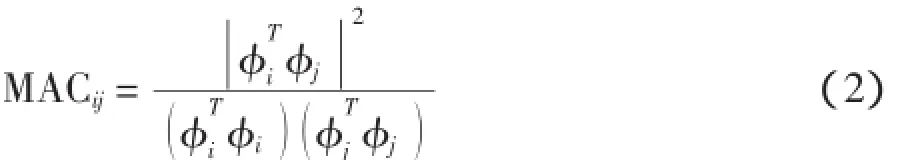
式中，φi，φj分别为第i阶和第j阶振型向量。

图9为机体自由状态下的Levy法、LSCF和理论模态的置信图。

由图9中可知，Levy法和LSCF的自置信度图中，同阶模态幅值相干系数都为1，其余值均近似于0；理论模态、Levy法和LSCF的互置信度图中，同阶模态幅值相干系数都大于0.8，其余值均小于0.15。

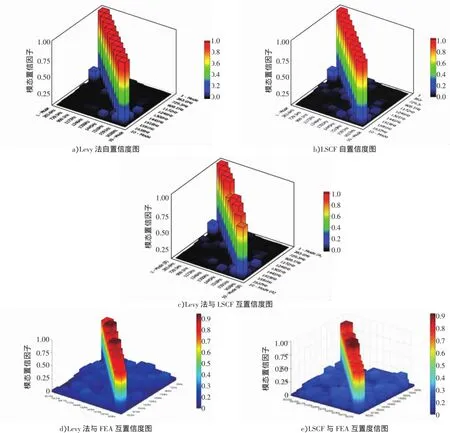
图9　置信度图

5　结论

1）多项式拟合法和最小二乘复频域法解得的模态参数吻合度较高。两者固有频率、主振型几乎相同，阻尼变化趋势一致。同阶模态幅值相干系数为1，不同阶模态幅值相干系数近似于0。

2）试验法和有限元法的结果比对发现，固有频率和主振型都有较高的吻合度。故机体有限元模型精度较高，可作为柴油机振动计算、噪声预测的基础。

3）YN38CRD型柴油机额定转速为3 000 r/min，即一阶激励频率为50 Hz。数据表明，机体的固有频率在359 Hz以上，远远大于系统的激励频率。但柴油机的燃烧压力激励近似为脉冲激振力，其含有丰富的频率成分，故对机体的影响不容忽视。

4）机体振动最大变形位置多集中于曲轴箱，与机体曲轴箱固定连接的油底壳刚度较小，故应对机体曲轴箱进行动态特性强化，以优化整机振声性能。机体气缸体的振动会使缸孔产生椭圆振动，影响缸套与活塞间的密封，引起气缸漏气、窜机油。

1张焕宇，郝志勇，李一民，等.490柴油机机体减振降噪研究［J］.振动与冲击，2012，3（7）：54-57

2毕凤荣，杜宪峰，邵康，等.基于形貌优化的低振动柴油机机体设计［J］.内燃机学报，2010，28（5）：459-463

3郑康，郝志勇，毛杰，等.基于声品质评价的缸盖罩NVH优化［J］.内燃机工程，2015，36（2）：98-102，110

4杜宪峰，舒歌群，卫海桥，等.基于模态方法的柴油机机体结构建模技术研究［J］.振动与冲击，2015，34（21）：157-161

5Peter Verboven.Frequency-domain system identification for modal analysis［D］.Brussels，Belgium：VRIJE University，2002

6肖正明，秦大同，武文辉，等.盾构机多级行星减速器箱体模态分析与试验［J］.重庆大学学报，2012，35（7）：37-42

7曹树谦，张文德，萧龙翔，等.振动结构模态分析——理论、实验与应用（第2版）［M］.天津：天津大学出版社，2014

8Bart Peeters，Herman Van der Auweraer，Patrick Guillaume，et al．The PolyMAX frequency-domain method：a new standard for modal parameter estimation［J］.Shock and Vibration，2004，11：395-409

9谢小平，韩旭，吴长德，等.基于PolyMAX方法的某轿车白车身实验模态分析［J］.汽车工程，2009，31（5）：440-443，447

10谢小平，韩旭，陈国栋，等.某商用车驾驶室白车身模态分析［J］.湖南大学学报（自然科学版），2010，37（5）：24-30

11王姗，舒歌群，卫海桥，等.六缸机缸体加强框对缸体振动噪声的影响分析［J］.内燃机学报，2010，28（6）：525-529

Experimental Modal Analysis of YN38CRD Diesel Engine Cylinder Block

Gu Yuanfeng，Wang Guiyong，Huang Gang，Bi Yuhua，Shen Lizhong
Yunnan Key Laboratory of Internal Combustion Engine，Kunming University of Science and Technology（Kunming，Yunnan，650500，China）

The finite element model is basically used as the basis for vibration calculation and noise prediction of diesel engine.And it is usually validated and modified by experimental modal analysis.In this paper，modal parameters of cylinder block of YN38CRD diesel engine were identified by polynomial fitting method and least squares complex frequency domain method，and compared with those obtained by finite element analysis.According to the modal assurance criterion，the modal parameters are validated.Result shows that the experimental data coincided with computational modal parameters，which indicates the accuracy of experimental and finite element mathematical model.Modal shapes comparison shows that the maximum deformation mostly occurred at crankcase，and elliptical vibration in the cylinder bore could lead to gas leakage and oily smoke.The study could provide a reference for optimizing vibro-acoustical characteristics of diesel engine.

Cylinder block，Experimental modal analysis，Polynomial fitting method，Least squares complex frequency domain method，Modal assurance criterion

TK421

A

2095-8234（2016）03-0080-08

云南省科技创新强省计划项目（2015AA024）.

古元峰（1993—），男，硕士研究生，主要研究方向为内燃机现代设计.

2016-04-13）