威布尔分布环境折合因子计算及其应用研究
吴英伟,齐杏林,崔亮,郑波
(1.军械工程学院,石家庄 050003;2.总装军械技术研究所,石家庄 050000)
威布尔分布环境折合因子计算及其应用研究
吴英伟1,齐杏林1,崔亮1,郑波2
(1.军械工程学院,石家庄 050003;2.总装军械技术研究所,石家庄 050000)
目的 对不同环境条件试验下的数据进行融合。方法 针对应用最为普遍的威布尔分布类型的环境折合因子进行研究,给出威布尔分布环境折合因子的定义,根据极大似然估计法对威布尔分布环境折合因子进行计算。结果 得出了相关环境折合因子的计算结果,在此基础上给出了应用环境折合因子进行数据融合的方法和步骤。结论 应用威布尔分布环境折合因子可以合理的对不同环境下试验数据进行融合,达到扩大试验样本的目的。
威布尔分布;环境折合因子;极大似然估计;数据融合
威布尔分布在可靠性工程中具有很强的适用性,已成为可靠性工程中应用最广泛的分布。威布尔分布可以从最弱环模型导出,最弱环模型认为整个系统的寿命取决于系统各个环节组成中的最薄弱部分,故障将首先发生在最薄弱部位,假如各环节同分布,那么系统寿命就服从威布尔分布。基于此背景,综合大量的实践说明,局部失效导致全局失效的元件、器件以及设备等都可用或近似用威布尔分布来描述其寿命分布。譬如对可靠性要求较高的军用产品,其寿命分布就服从威布尔分布[1—5]。在研发时,往往需要在不同环境下进行试验,定型后在不同环境下储存也需要实施性能检测,但是限于成本,样本数相对较少,这就需要应用环境折合因子对不同环境下试验数据进行折算和融合。因此,对威布尔分布环境折合因子进行研究具有十分重要的理论和工程意义[6—9]。
1 定义
若产品的寿命分布为威布尔分布,则其分布的密度函数[10]为:
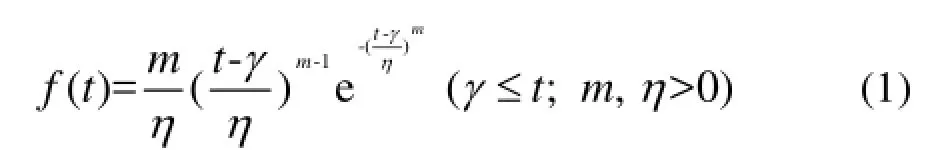
对应的威布尔分布函数为:
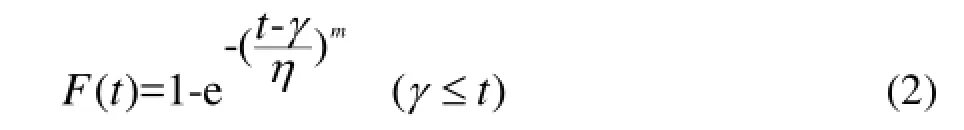
式中:m为形状参数,其取值不同能够改变密度曲线的形状,包含指数分布、正态分布等特殊情况;η为尺度参数,能够改变比例常数;γ为起始位置参数,也称为最小保证寿命,m,η固定时,γ取值不同,密度曲线形状无变化,位置发生平移。
威布尔分布的均值和方差分别为:
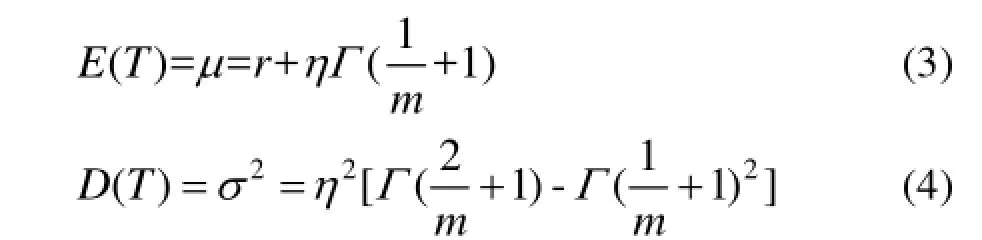
式中:Γ(x)为伽马函数,由伽马函数表可查得其相应函数值。
基于以下3个假设讨论环境折合因子[11—12]:分布同族假设,即环境不同,产品寿命分布都属于威布尔分布类型,相关参数不同;失效机理不变假设,即环境不同,产品失效机理不变;Nelson假设,即已累积的失效和当前应力决定着产品剩余寿命,而与累积方式无关。
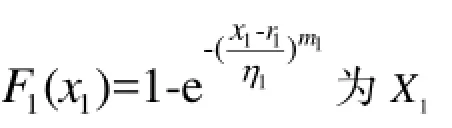
2设X2经过某函数h( X2)变换后,与X1为同分布的随机变量,此时有[13]:

可得:
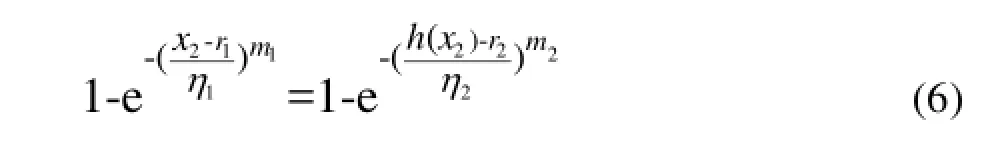
4)中国女篮需要提升与强化主力小前锋2分球的得分能力和组织后卫与得分后卫的3分球得分能力,加强身体对抗能力,提高身体对抗中的投篮命中率。
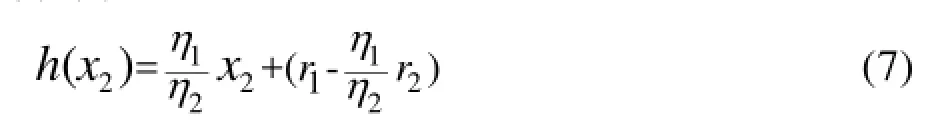
此时式(7)可表示为:

(K,b)称为二维环境折合因子。将K,b根据式(3)和(4)作变换可得:

可以发现,K随着方差的改变而变化,而b是由均值和方差的变化共同决定的。在工程实际应用中,一般取γ=0,此时称为两参数威布尔分布,有:

2 计算
假设从某产品中随机抽取n件在某种环境下进行截止时间为ts的定时截尾寿命试验,共有r件失效,r件产品的失效时间按从小到大排序得[14—15]:t0 通过对m,η求偏导,可以得到对应似然方程为: 整理简化后,有: 由式(15)可以发现,若在某一环境下,产品出现零失效情况,方程组的求解将无法进行,此时可将γ=0情况下式(2)变形并取对数[11],得: 式(17)可表示为: 设产品试验截尾时间ti( i=1,2,…,n),对应时间段内失效率为F( ti),利用式(17)可以求出参数和,代入式(11)即可求出环境折合因子。这种方法适用于失效数为零的情况,可与极大似然估计方法互为补充,但该方法精度有限,只有样本量较大情况下才能有较好的计算精度。 环境折合因子指的是不同环境下产品寿命折合系数。假设从某产品中随机抽取ni( i=1,2)件在两种不同环境下进行定时截尾寿命试验,到时间 ts停止试验,对应失效数分别是ri( i=1,2),失效时间记为ti, j(i=1,2;0<j≤ri),试验数据可表示为: 与环境1下的试验数据融合[15],有: 上述数据可视为在环境1下,样本数n1+n2,截止时间为tm(K≥1时,,否则,)的定时截尾寿命试验,失效数为r1+r2。 工程上认为,这种融合方法比较合理,因为它既没有改变样本的失效个数,也没有使试验总时间冒进,同时数据样本量由原来的n1扩大到n1+n2,可以有效提高可靠性评定的精度。 弹药等对可靠性要求较高且成本较昂贵的产品,在试验和抽检过程中,样本量往往不大。与此同时,应用环境的不同导致储存环境呈现多变性,因此科学地评估产品储存环境折合因子,对于准确评定产品可靠性具有重要意义。文中针对不同储存环境下威布尔分布试验数据融合问题展开研究,分析了环境折合因子的定义、计算过程及其应用方法,表明了应用环境折合因子法进行数据融合的合理性和可行性,能够达到扩大试验样本量的目的,具有重要的工程意义[16]。 [1]韩庆田,李文强,卢洪义.逆Weibull分布环境因子及其统计分析[J].装备环境工程,2011,8(6):54—57. HANQing-tian,LIWen-qiang,LUHong-yi. Environment Factor of Inverse Weibull Distribution and ItsStatisticalAnalysis[J].EquipmentEnvironmental Engineering,2011,8(6):54—57. [2]郭恒晖,李传日,庞月婵,等.基于极大似然估计的加速因子计算方法[J].装备环境工程,2014,11(5):49—53. GUO Heng-hui,LI Chuan-ri,PANG Yue-chan,et al. Calculation of Acceleration Factor Based on Maximum LikehoodEstimation[J].EquipmentEnvironmental Engineering,2014,11(5):49—53. [3]丁光雨,陆山,撒彦成.同类异型产品环境因子的确定方法及应用[J].装备环境工程,2013,10(5):61—64. DINGGuang-yu,LUShan,SAYang-cheng. Determination Method of Environmental Factors for Same Kind Products and Its Application[J].Equipment Environmental Engineering,2013,10(5):61—64. [4]马志宏,李金国,李静,等.内外场综合可靠性试验方法分析与探讨[J].环境技术,2011,10(5):25—29. MA Zhi-hong,LI Jin-guo,LI Jing,et al.Analysis andDiscussion of Integrated Reliability Evaluation Method of the Internal and External Field Test[J].Environmental Technology,2011,10(5):25—29. [5]魏郁昆.系统可靠性分析中环境因子评估方法研究及软件实现[D].成都:电子科技大学,2014. WEI Yu-kun.Estimation of Environment Factor in System Reliability and Software Realization[D].Chengdu: University of Electronic Science and Technology of China, 2014. [6]邬洪涛.混合失效率及其单调性研究[D].成都:西南交通大学,2010. WU Hong-tao.Research for Mixed Failure Rate and Monotonic[D].Chengdu:Southwest Jiaotong University, 2010. [7]田丰.可靠性试验数据处理与数据充分性[D].沈阳:东北大学,2007. TIAN Feng.The Data Processing of the Reliability ExperimentsandItsSufficiency[D].Shenyang: Northeastern University,2007. [8]扈延光,王志敏,闫蓓.可靠性评估中环境因子的一种工程确定方法[J].科学技术与工程,2005(8):473—475. HUYan-guang,WANGZhi-min,YANBei.An Engineering Method to Determine Environment Factors for Reliability Assessment[J].Science Technology and Engineering,2005(8):473—475. [9]茆诗松,汤银才,王玲玲.可靠性统计[M].北京:高等教育出版社,2008:129—130. MAOShi-song,TANGYin-cai,WANGLing-ling. Reliability Statistics[M].Beijing:Higher Education Press, 2008:129—130. [10]盖京波,王善.韦布尔分布的环境因子[J].安全与环境学报,2002(3):58—60. GAI Jing-bo,WANG Shan.Environmental Factors for WeibullDistribution[J].JournalofSafetyand Environmental,2002(3):58—60. [11]李湘宁,李晓斌.威布尔分布的战术导弹可靠性试验信息融合方法[J].火力与指挥控制,2014,39(12): 153—155. LI Xiang-ning,LI Xiao-bin.Research on Environment Factors and Engineering Practice about Tractical Missile Based on the Weibull Disrtribution[J].Fire Control& Command Control,2014,39(12):153—155. [12]李凤.环境因子估计理论及其在可靠性评估中的应用[D].西安:西北工业大学,2007. LI Feng.Environmental Factors estimation theory and Its applicationinReliabilityEvaluation[D].Xi'an: Northwestern Polytechnical University,2007. [13]王健,李湘宁.Weibull分布环境因子工程计算方法[J].现代防御技术,2012(3):53—56. WANG Jian,LI Xiang-ning.Engineering Calculation MethodforEnvironmentalFactorsofWeibull Distribution[J].Modern Defence Technology,2012(3): 53—56. [14]戴树森,费鹤良.可靠性试验及其统计分析(下)[M].北京:国防工业出版社,1984:18—22. DAI Shu-sen,FEI He-liang.Reliability Testing and StatisticalAnalysis(Below)[M].Beijing:National Defense Industry Press,1984:18—22. [15]郑波,刘冬青,李明,等.一种确定引信储存环境因子的理论方法[J].探测与控制学报,2006(2):16—18. ZENG Bo,LIU Dong-qing,LI Ming,et al.A Theoretical Method of Determining Fuze Storage Environmental Factor[J].Journal of Detection&Control,2006(2):16—18. [16]翟国富,王淑娟,姜守旭,等.电器可靠性失效分析中极大似然估计方法的研究[J].中国电机工程学报, 2001(3):90—92. ZHAI Guo-fu,WANG Shu-juan,JIANG Shou-xu,et al. The Research on Method of Maximum Likelihood Estimation for Apparatus Reliability Failure Analysis[J]. ProceedingsoftheChineseSocietyforElectrical Engineering,2001(3):90—92. Calculation andApplication of Environment Conversion Factors for Weibull Distribution WU Ying-wei1,QI Xing-lin1,CUI Liang1,ZHENG Bo2 Objective To fuse the test data under different environmental conditions.Methods This paper discussed the environment conversion factors for Weibull distribution which is the most widely used distribution.First,the environment conversion factors for Weibull distribution were defined.Then,the environment conversion factors were calculated by the maximum likelihood estimation.Results Calculation results related to environmental factors were obtained,based on which the methods and procedures for application of environment conversion factors were given.Conclusion Data fusion under different environmental conditions by environmental factors of Weibull distribution was reasonable,so as to achieve the purpose of expanding the test sample. Weibull distribution;environment conversion factors;maximum likelihood estimation;data fusion 2015-12-10;Revised:2016-2-19 10.7643/issn.1672-9242.2016.04.015 TJ01;TB114 A 1672-9242(2016)04-0088-04 2015-12-10; 2016-2-19 吴英伟(1991—),男,吉林长春人,硕士研究生,主要研究方向为信息感知与控制。 Biography:WU Ying-wei(1991—),Male,from Changchun,Master graduate student,Research focus:information perception and control.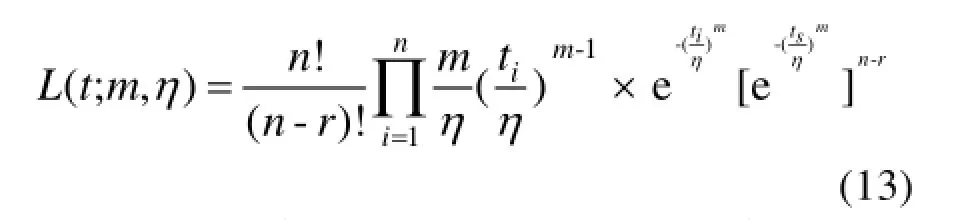
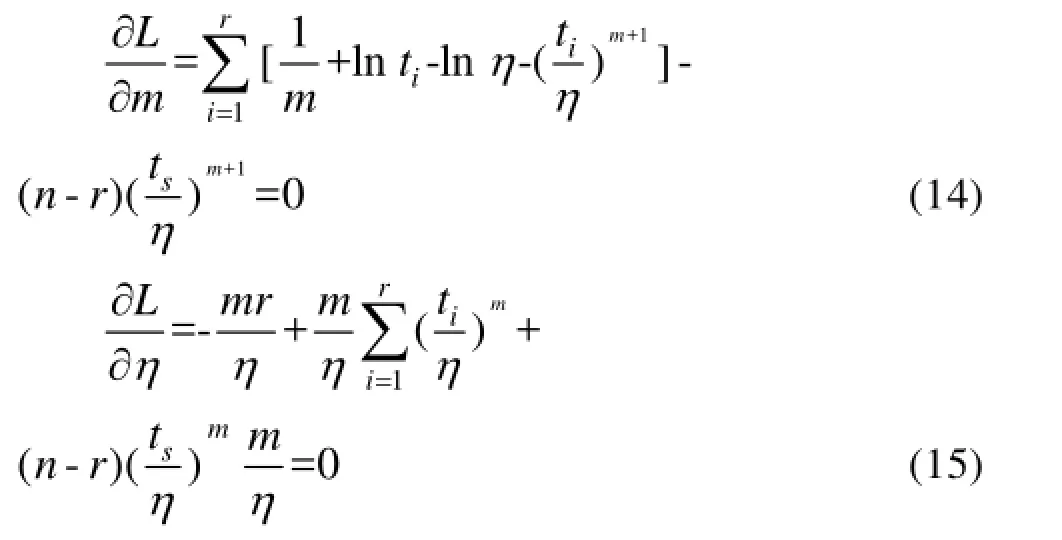
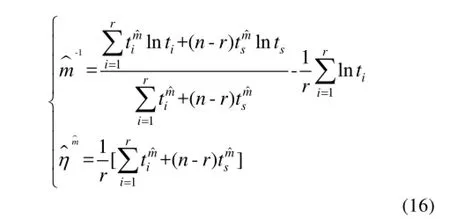
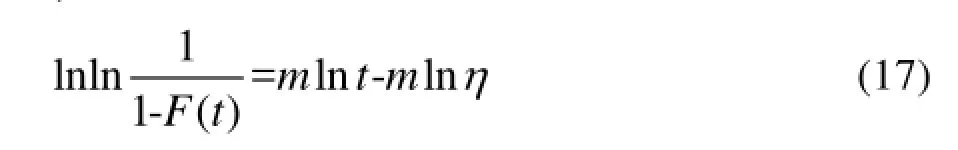

3 应用
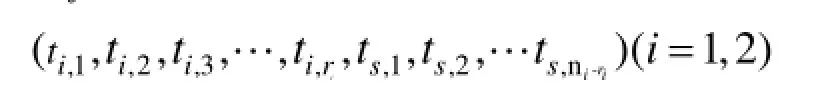
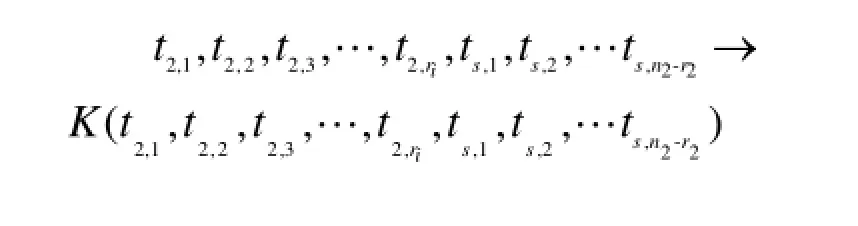
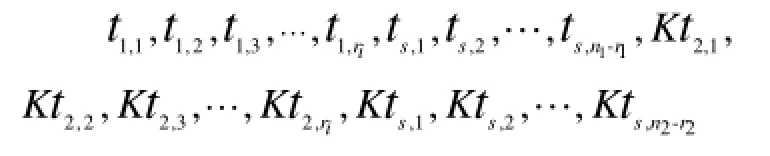
4 结语
(1.Ordnance Engineering College,Shijiazhuang 050003,China;
2.Ordnance Technology Research Institute,Shijiazhuang 050000,China)

