城市轨道交通共线交路运行图的优化与编制

张晓倩　崔炳谋

1(兰州交通大学交通运输学院　甘肃 兰州 730070)2(兰州交通大学交通信息研究所　甘肃 兰州 730070)



城市轨道交通共线交路运行图的优化与编制

张晓倩1崔炳谋2

1(兰州交通大学交通运输学院甘肃 兰州 730070)2(兰州交通大学交通信息研究所甘肃 兰州 730070)

传统铺画城市轨道交通共线交路运行图中考虑的因素较简单，针对其不能满足不断壮大的城市轨道交通网络的问题，先运用顺序推点法计算出列车在各站的到发时刻，然后分析为满足一条线路上的客流特征组织列车开行两种或两种以上交路的必要性，并根据折返站的容车能力以及折返时间等现场因素，提出适合于实际问题的模型与算法。实例铺图结果表明，相对于传统的车底交路勾画模型与算法，该模型与算法可明显减少车底在各折返站的总停留时间，从而最大限度地减少车底的运用数量。

城市轨道交通时刻表大小交路折返站容车能力共线交路运行图

0　引　言

城市轨道交通共线交路是指某条线路在分析客流特征的基础上，组织列车开行两种或两种以上的交路方式，并且在两交路上有一段相同的运行区段。而共线交路运行图是在共线交路的情况下，列车在固定的基本站与折返站之间担任旅客运输任务的运行综合计划，它是城市轨道交通行车组织的基础，它的编制质量将直接影响列车的运输效率，并对提高线路服务水平，实现安全生产目的具有重要意义。

列车共线交路运行图的铺画相对于国家铁路要简单一些，但是，由于系统运行环境是城市地区，线路客流的波动随节假日变化较大，为满足轨道交通列车有序运行及旅客出行需求，列车运行间隔需要频繁调整[1]。有些文献对同一线路的共线交路情况下列车首末班车与换乘节点站衔接方案的优化、车场的有效利用以及列车延误影响等问题，对共线交路情况下列车运行图的铺画流程和方法进行了探讨[2]。还有文献对城市轨道交通列车运行图计算机编制过程中的行车间隔，大小交路列车开行数量的匹配等问题的研究[3]。文献[4]利用运行图周期分析法，提出计算多交路条件下城轨通过能力和车底数量的数学模型。

事实上，关于城市轨道交通共线交路运行图编制的模型以及方法的文献还相对较少或者考虑的因素较简单，越来越不能满足不断壮大的城市轨道交通网络，实用价值不强。

本文在时刻表的推算过程，以及车底交路的模型建立中考虑了城市轨道交通网络列车运行区段内出现的客流不均衡现象，并且在已知时刻表计划的基础上，为某时间段、某空间范围内组织安排一定数量的列车车底，之后为这些车底分配相应的列车车次、出入车辆段或者停车场等，以此来实现列车车底资源的优化应用。在计算机编图优化中，对平峰时段与高峰时段进行了划分，定义底图结构，确定大小交路，依据列车在基本站的发车间隔以及交路客流特征确定大小交路开行比例，再根据车底运用方式计算车底总停留时间最少，最后铺画完成运行图以及出入库线。

1　时刻表推算方法

由于运行区间线路状况不同，即同一区间在不同的运行方向上列车的总运行时间有所不同，则有列车从车站i到车站j的总运行时分：

(1)

同一车站的列车的停站时分受区间运行方向上的客流的密度大小影响也有所差异，因此列车k在车站i的停车时分：

(2)

上行列车k到达车站i的时刻：

(3)

上行列车k从车站i发出的时刻：

(4)

同理，可用上述方法推算出下行列车在中间各车站的到、发时刻。

时刻表是多个列车车次的时间安排，它是运营部门向旅客提供列车在各站到发时刻的一种时间表格。为了使时刻表呈现得更加明了，方便运营工作人员的工作，在时刻表数据计算完成后，运用计算机将它以图形的形式展现出来，这就是运行图的一部分图形展示，即运行线。

可见，时刻表实际上是运行图的另一种表现形式，它是运行图铺画的基础数据。

2　车底交路优化模型

城市轨道交通车底是指固定编组、循环使用、不进行分摘的车列。而车底交路是为实现运行图规定的任务，为每一运行计划，即每一条运行线安排列车服务，且运行区段固定，基本段和折返段必须有足够的整备时间。

一般地，影响城市轨道交通车底交路的因素除了时间约束、空间约束外，还有很多其他约束。比如折返站的容车数限制、折返时间限制等。这些影响因素如果考虑不全，对运行图的优化编制都会产生影响，所以本文的车底交路优化模型以符合城市轨道交通列车开行特点为基础，加快车底的周转，最大程度地减少车底的数量为目的。

假设车底套跑运用，即两个或者两个以上的列车，使用同一车底。下面以计算出的时刻表数据为基础，定义相关参数：

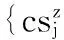
k表示全天运营时间段内到发列车集合，k=kd∪kf，其中kd为到达列车集合，kf为出发列车集合；

tz定义为列车在折返站z允许的最长停留时间；

rz表示折返站z的最大容车数；

w表示到达列车满足折返条件时，在折返站不等待出发而选择先入库，后出库的列车集合；

v表示列车因选择出入库，产生燃油、人员等损耗所给与的惩罚值；

m表示折返站数量；

首先我们引入一组变量：

其二，已有研究表明，教师在理解和讲授统计和概率方面存在许多困难，其主要难点在于数据分析观念的渗透，这就需要教师不断提高自己的专业素养.首先，教师自身需要有数据分析观念的意识.其次，教师应具备引导学生形成数据分析观念的能力.因此，如何对教师进行统计教育和培训是一个巨大的挑战.职前教师教育应加强理论和应用统计学的学习，培养统计思维和教学观念等.在职教师培训应以实际问题为导向，注重教师的实践经验，合作学习和交流，从而使教师能够自我分析和反思.

其中，i∈kd或(kd⊕w),j∈kc或(kc⊕w)，其中定义⊕表示连接运算，即到达列车连接入库；

当i∈kd，j∈kf时：

(5)

当i∈(kd⊕w)，j∈(kc⊕w)：

(6)

与铁路机车交路问题相比较，城市轨道交通折返站上的车底交路问题有一个明显不同，就是在折返站上必须考虑容纳车底数的限制，以保证列车按图运行。例如，某折返站在同一时间最多容纳4列车底，如果多于4列，应及时安排入车辆段。

对折返站容车能力描述：在高峰时段向平峰时段的过渡时间段中,车站的到达间隔时间远小于出发列车的出发间隔时间,车底有可能在折返站上“堆积”[5-8]，假设这时存在的折返方式如图1所示。

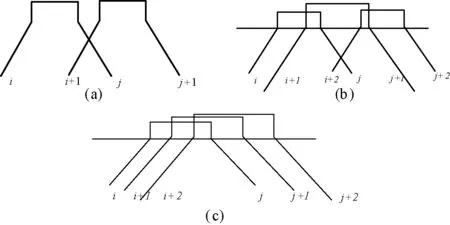
图1　车底折返方式

目标函数：

s.t：

列车必须由一组车底为其服务：

(7)

(8)

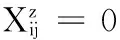
(9)

折返站容车数约束：

max(r′,r″,r‴)≤rz

(10)

到达列车入库约束：

(11)

折返时间约束：

(12)

3　车底交路优化算法设计

该问题可以简化为指派问题求解，但是求解指派问题的方法较多且最优解有多个，大多数情况下求得的最优解并不能很好地适用于实际问题。而城市轨道交通运输问题涉及的变量多而复杂，并且在实际的问题中会产生大量的不确定因素，运用常规的算法设计不能满足实际问题的特点及运输规律，所以本文从整体优化的思想出发，以优化模型为依据，设计适合于该实际问题的算法来优化运行图的编制质量。

本文算法步骤如下：

(1) 在到达列车集合kd中，取到达列车i=1，即从第一列到达折返站z的列车开始，依次对每一个到达列车i(i=1…k)，找到出发列车集合kf中j=1的列车；

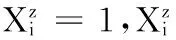
Step6列车在区段端点都有出入库线或与对向列车相连。

4　实例分析

以上海市轨道交通一号线春季运营计划为研究背景，模拟铺画共线交路运行图，以验证时刻表计算的合理性与车底在折返站作业组织的正确性。假设下行线路1始于富锦路，止于外环路，上行线路1反之；上行线路2始于外环路，止于上海火车站，下行线路2反之。线路运营全长32.53km，共有车站27座[9]，线路两端设两车库(停车场和莘庄)，其中富锦路(简称“富”)，外环路(简称“外”)作为基本站(兼作折返站)，上海火车站(简称“火”)只作为折返站，折返站最大容车数为3。

在此，共线交路问题为两个单一的交路嵌套在一起的大小交路问题。大小交路的起点相同，终点不同。如图2所示。

图2　交路方式

同时为了提高城市轨道交通列车的服务水平，尽量要保证均衡的行车间隔。所以，在铺画运行图时，在每一个运行时段内，不同类型交路，列车发车间隔符合一定的比例关系，例如1∶1，1∶2等[2]，实例基础数据如表1、表2所示。

表1　交路开行比例与发车间隔

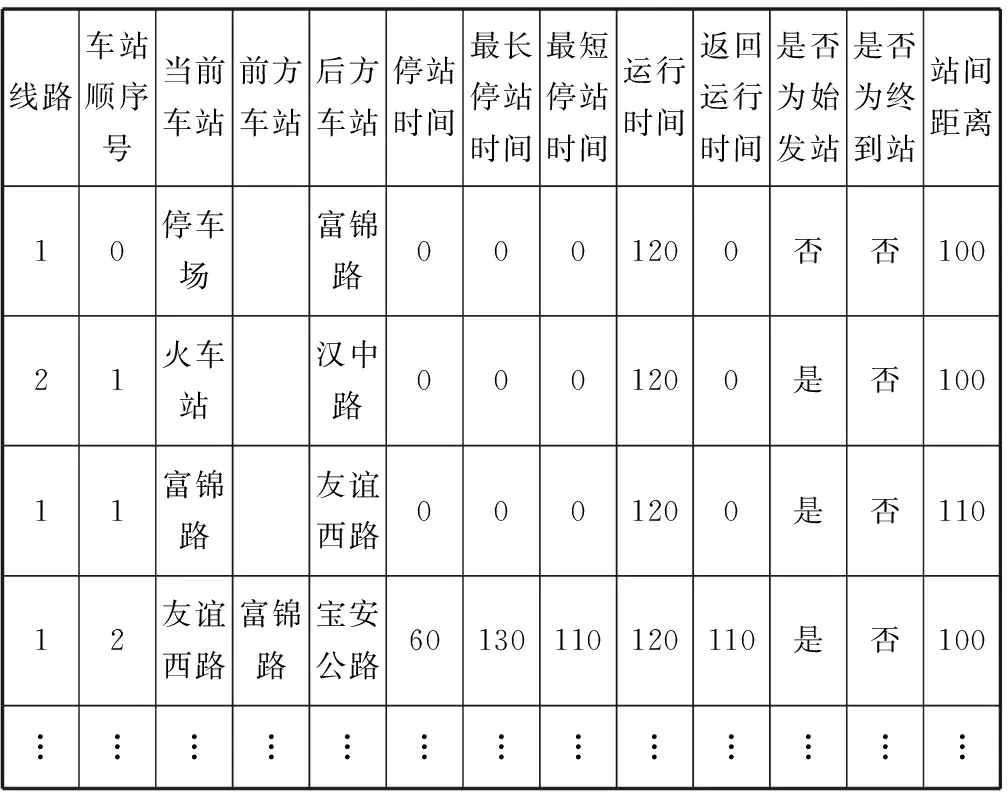
表2　站线关系表

基于上文中的时刻表推算方法，利用计算机计算全天运营时间段内(包括平峰时段和高峰时段)的时刻表，如表3所示。

表3　列车时刻表

列车时刻表实际上是列车运行图的另一种表现形式，所以它是计算机铺画运行图的基础数据，在上文中已计算出了时刻表，现将其转化为列车运行图。

计算机编程过程中为更逼真地模拟出城市轨道交通列车运行图，现设横轴为时间轴，因为城市轨道交通列车开行密度较大，所以将该时间轴定义为一分格，即每格为一分钟，纵轴设两个参数，站名与站间运行时间，然后通过计算机进行了基础时分参数，列车运行间隔等数据的维护，据此计算机铺出运行图以及出入库线。

当运行图铺画完成后开始勾画交路。根据车底交路数学模型计算出每列车在折返站的最少停留时间，然后运用上文中的车底交路算法在折返站富锦路、上海火车站，莘庄勾出了交路，局部放大图如图3所示。

图3　共线交路运行图

图4为富锦路折返站的容车数情况。以 10∶32到11∶17这个时间段为例，富锦路折返站最大容车数为3，如列车132、106和116或列车134、136和120同时在站。

图4　折返站容车数情况

最后从铺画的图中可以得出共需21个列车来完成该城市轨道交通春季运营计划。实例铺图结果表明，相对于传统的车底交路勾画算法，本文的算法可明显减少车底在各折返站的总停留时间，这在一定程度上就相当于减少了车底的运用数量，这也对节省企业成本，提高旅客运输效率具有重要意义。并且与手工编图对比，计算机编图能较好地满足实际运行要求，并能实现自动化编制，较大程度上减轻了手工编制的劳动强度，所以这将会在为后轨道交通研究中提供更多的理论与应用基础。

5　结　语

综上所述，城市轨道交通共线交路运行图的优化目的在于减少车底在各折返站总停留时间。据此，本文以上海轨道交通一号线列车开行特点以及交路方案为背景，简化了模型的建立与约束条件的分析，设计求解算法，在计算机铺画过程中考虑不同交路开行比例的合理安排、开行间隔、折返站容车数等问题，来达到理想中的车底运用目的。

[1] 许红,马建军,龙建成,等.城市轨道交通列车运行图编制的数学模型及方法[J].北京交通大学学报,2006,30(3):10-14.

[2] 江志彬,徐瑞华,吴强,等.计算机编制城市轨道交通共线交路列车运行图[J].同济大学学报,2010,38(5):692-696.

[3] 徐瑞华,江志彬,朱效洁,等.城市轨道交通列车运行图计算机编制的关键问题研究[J].城市轨道交通研究,2005(5):31-35.

[4] 程婕,彭其渊,赵军.城市轨道交通列车交路优化模型[J].西南交通大学学报,2013,48(6):1116-1121.

[5] 王川.城市轨道交通列车运行图编制模型和算法研究[D].长春:西南交通大学,2008.

[6] 崔炳谋.机车周转图的计算机优化算法[J].铁路计算机应用,1998,8(2):16-18.

[7]SalzbornFJM.Timetablesforsuburbanrailwaysystem[J].TransportationScience,1970,4(12):383-402.

[8]WongRachelCW,YuenTonyWY,FungKwokwah,etal.Optimizingtimetablesynchronizationforrailmasstransit[J].TransportionScience,2008,42(1):57.

[9] 徐瑞华,马兴峰,宋键.上海轨道交通明珠线共线运营方案[J].城市轨道交通研究,2003(6):682.

SHARD-PATHROUTINGTIMETABLEOPTIMISATIONANDDESIGNINGOFURBANRAPIDTRANSIT

ZhangXiaoqian1CuiBingmou2

1(School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,China)2(Institute of Traffic Information,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,China)

Thefactorsconsideredintraditionalsharedpathroutingtimetableofurbanrapidtransitarerelativelysimple,howeveritcannotmeetthegrowingproblemofurbanrailtransitnetworks.Aimingatthisissue,weusedthepushorder-pointmethodtocalculatetrains’arrivalanddeparturetimeateachstationfirst,thenanalysedthenecessityofopeningthelinesoftwoormorepathroutingtomeetthecharacteristicsofpassengersononeline,andinaccordancewiththefieldfactorssuchascarcapacityandtimeofturnbackstation,webuiltamathematicalmodelanddesignedanalgorithmwhichweresuitableforpracticalproblems.Resultsinpictureshowedthatcomparedwithtraditionalmodelsandalgorithmsofvehiclerouting,thismodelandalgorithmcouldobviouslyreducethetotalresidencetimeofvehiclesateachturnbackstationandthusminimisedtheamountofvehicles.

UrbanrapidtransitTimetableLongandshortroutingTurn-backcarcapacityShared-pathroutingtimetable

2014-06-28。国家自然科学基金项目(61263027)；高等博士学科点专项科研基金新教师类课题(20126204120002)；甘肃省自然科学基金项目(213227)。张晓倩，硕士生，主研领域：交通运输规划与管理。崔炳谋，教授。

TP3

ADOI:10.3969/j.issn.1000-386x.2016.03.058