遗传规划自适应建模的JAVA实现及在股票价格预测中的应用

葛志远　陈会涛

(北京工业大学经济与管理学院　北京 100124)



遗传规划自适应建模的JAVA实现及在股票价格预测中的应用

葛志远陈会涛

(北京工业大学经济与管理学院北京 100124)

针对如何将遗传规划方法与时间序列有效结合，构建基于遗传规划的时间序列自适应模型，并通过Java语言辅助算法的实现。相比之前遗传规划算法，采用平均值法改进初始群体的生成方式，使变异概率随着进化代数的增加而递减，且加入并行计算思想。在算法流程的核心计算环节,将适应度值的计算、个体的复制、交叉、变异操作都从线程的粒度来进行，基于实际运行效果来看，CPU多核运行明显，算法能够充分利用多处理器、多核进行计算，提高了运行效率。将改进的遗传规划模型应用于我国股票市场上股票价格的预测，将预测结果与经遗传算法优化的神经网络方法和传统遗传规划方法进行比较，结果证明改进遗传规划方法的预测精度更高，且能够更直观地表达输入与输出之间的关系。

遗传规划时间序列自适应建模股票价格预测

0　引　言

时间序列分析是指通过描述分析历史数据随时间变化的规律，预测事物的未来发展趋势，其在经济预测领域的研究过程中发挥着重要的作用。在股票市场上，时间序列分析可以用于对股票的未来价格趋势进行预测，其结果可为股票市场的管理者和投资者提供决策依据。

然而由于股票市场是一个比较复杂的非线性非平稳系统，它同时受多种因素的交互影响，有些因素较容易度量，而有些因素却难以量化。如果对其进行科学的计算和评价,仅用传统的统计理论和方法已不能满足对该领域进行深入研究的需要，迫切需要前沿理论和新技术的充实。

从股票预测方法的研究现状来看，国内外已有其他学者运用不同的方法对股票市场进行预测研究。Khashei等人[1]认为ARIMA模型能够较好地处理金融时间序列数据的非线性性质,将ARIMA应用于金融时间序列的分析。Sun等[2]使用RBF神经网络模型和K均值算法对上证股票价格指数进行预测。尚朝辉等[3]使用遗传规划构建了基于遗传编程理论的股票技术交易模型，证明该模型可以为股票买卖提供策略。Kazem等人[4]建立了基于支持向量机的预测模型来预测股票的市场价格，并以微软的收盘价进行实证研究。肖菁等[5]运用遗传算法优化神经网络的权值和阈值建立了改进的三层BP神经网络股票预测模型。Mirchandani等人[6]使用遗传算法优化神经网络，建立股票价格预测模型，并以孟买股票市场实证研究，结果显示预测准确率介于50%～80%之间。

通过查阅分析相关文献，发现基于统计学的股票时间序列的研究一般是建立在股票收益率是独立的、符合正态分布的假设上；支持向量机方法的长记忆性较差且实施大规模训练样本较难，比较适合对小样本数据进行学习和预测。文献中，关于遗传规划算法在股票价格预测领域的研究，大多数研究者是把遗传算法与神经网络相结合，构建出混合模型。但是通过分析发现，在使用遗传规划算法优化神经网络方法的过程中，需要对问题本身有深刻的了解和很好的判断，整个混合系统的性能要依赖于其他因素，难以使得所有因子达到最优化，一般比较难获得较好的ANN模型。且神经网络方法本身是一种黑盒的方法，对于表达并分析被预测系统的输入与输出之间的联系有一定的难度，所以也较难对最终的结果进行完整的解释和检验。

遗传规划(GP)是从遗传算法(GA)中演化和发展起来的一种搜索寻优技术[7]。两者的主要不同之处是个体表示结构和对数据的处理方式不同[8]。遗传算法是使用定长的字符串(通常是二进制)来描述问题，而遗传规划是用广义的层次化计算机程序来描述问题，遗传算法的这种固定的大小，限制了它的应用，使它无法描述一些大小结构变化的问题，缺乏动态可变性。同时由于要事先对字符串的长度进行估计，可能会使结果不够准确，甚至找不到全局最优解，而遗传规划恰好弥补了此方面不足。

基于遗传规划的自适应建模在很多领域均有应用价值。遗传规划方法有着强大的符号回归和处理非线性的能力，可以容易地显性表达输出变量与输入变量间的非线性关系。近年来许多学者对遗传规划算法及应用做了大量的研究工作，在实际的应用中取得了很大成功，如今它已成功地被应用于预测[9]、分类[10]、机器学习[11]、图像处理[12]以及数据挖掘[13]等领域。

本文首先介绍了基于遗传规划的自适应建模算法,将遗传规划与时间序列相结合,构建了基于遗传规划的时间序列自适应模型，并使用Java语言辅助GP自适应算法的实现。然后将GP算法模型应用于我国某支股票价格的预测，相比传统遗传规划算法和GA优化神经网络方法，该算法具有良好的结构逼近性能和较高的预测精度。

1　基于遗传规划的时间序列自适应建模

遗传规划的基本原理是，首先随机产生符合所要解决问题环境的初始群体，构成算法的搜索空间。该群体的每个个体都有一个适应度值，按照“优胜劣汰”的选择法则，用三种遗传算子依次处理拥有较高适应度值的个体，然后产生下一代群体,直到达到所设定的终止条件则结束循环。遗传规划最重要的特点是群体中的个体是用动态的树状结构组成，树状结构的层和节点都是可以动态变化的。

遗传规划方法的主要步骤如下：

(1) 确定个体的表达方式。遗传规划算法最常见的编码形式为由列表和原子构成LISP的S表达式。其中，列表对应树结构的非叶子节点，原子对应树结构的叶子节点。非叶子节点由运算符和初等函数组成，叶子节点包含变量与常量，通常为适用于问题空间领域的最基本元素。

(2) 随机生成初始群体。非叶子节点集和叶子节点集中的基本元素按一定的随机选择方法组合生成初始个体，初始个体达到规定的数目之后组成一个初始群体。本文对传统算法进行改进，采用平均值法生成初始群体：即首先生成M个个体,求它们的平均适应度,当新生成个体的适应度比当前平均适应度值大的时候，个体即被保留下来。重复此过程,直到保留下来的个体数达到M个为止。此种产生初始群体的方法对于每组个体而言,组平均适应度是一个逐步提高的过程,可以提高初始种群个体的整体适应度和算法的整体收敛效率。

(3) 个体适应度值计算。适应度值是衡量个体对环境适应能力强弱的指标，是个体表达式逼近真实解的近似程度。本文引入适应度函数：

其中yi表示第i个观测值，T表示观测值的个数，yi是根据函数表达式得到的与yi相对应的第i个预测值，u表示观测值的平均值。

(4) 根据设定的遗传参数对群体中的个体进行复制、交叉和变异遗传算子操作，以此产生新一代的个体。本文把当前种群中具有最高适应度的函数直接保留到下一代,以保证每代中的最优个体不被破坏。其中，变异操作属于辅助算子，对保持种群的多样性功能起着重要的作用，在进化初期，个体的适应度相对较差，因此，本文在进化初期采用较大的变异概率对群体中适应度较差的个体进行变异以加快进化速度。

(5) 重复(3)和(4)，直到满足设定的终止准则，终止准则一般有：运行进化到规定迭代次数或进化达到规定的允许误差。

遗传规划的整体工作流程如图1所示。

图1　遗传规划算法流程图

基于遗传规划算法的整个建模过程不依赖于具体问题领域的特定知识即可动态地生成搜索空间。从演化结果和外推与内插的特性方面来看，遗传规划建模方法比人工神经网络更优越的地方是其能得到简单的显式表达式。在这样的背景下，使用遗传规划算法进行数据拟合，可以不需要确定方程的具体结构，而只需将数据交给计算机，设定一个精度，然后在经过几十代甚至几百代后，就可以得到符合自由曲线变化规律的数学表达式。

我们根据如上所述的基于遗传规划的自适应建模算法，结合时间序列元素，建立股票价格预测模型。根据需求功能特性的描述，将算法的功能划分为四个模块：模型个体的编码模块、基于遗传规划的算法模块、系统的控制界面以及数据接口模块。如图2所示，算法的基本原理是通过遗传规划算法的搜索求解功能，通过研究对象自身的历史数据，来寻找符合研究对象特征的最优模型。

图2　基于遗传规划的股价预测模型及算法模块划分

2　算法设计

遗传规划方法的任务是，从许多候选的自动生成求解实际问题的计算机程序所组成的搜索空间中，通过优化寻找出一个具有最佳适应度的计算机程序。Java语言是一种可以撰写跨平台应用软件的面向对象的程序设计语言。因此本文使用Java编程语言[14]辅助算法的实现，通过面向对象的思想和方式，帮助我们实现对所要解决的问题进行抽象与建模，也更利于用我们易理解的方式对算法进行分析、设计与编程。同时开发了MySQL数据库接口，建模采用的原始数据保存在MySQL数据库中，在安装了标准的Java1.7虚拟机的电脑上运行。

2.1结构设计

(1) 二叉树

本算法用到的典型的数据结构是二叉树结构。系统使用二叉树结构来描述模型，即：树结构中的非终端节点为函数，包括简单的计算操作(﹢、-、*、/)、函数(sin,cos,tan,exp,power,log)等。树结构的终端节点为变量或者常量，从而使得一棵二叉树即是一个模型表达式。

在上述结构中，简单的计算操作是二元的，函数有一元的，也有二元的。由这些元素组成的树结构中，每个节点至多有两个孩子节点。本文直接采用二叉树来表示。

(2) 数组列表ArrayList

遗传规划算法的个体种群采用ArrayList结构。ArrayList结构是一种线性数据结构形式，它会在删除掉某些元素时自动缩小，这样就不必检查个体种群中所有的元素，只需要查询它是否带有要寻找中的值就好。

(3) 矩阵Matrix

原始数据采用矩阵的数据结构来表示。不论是待拟合系统的输入数据，还是输出数据，均采用矩阵结构。采用矩阵结构来描述数据的另一个好处是可扩展性。例如对于多变量联立方程组模型，矩阵结构就能够很轻松实现，而对于向量式的数据结构就难以描述多变量联立方程组。

2.2数据接口设计

本算法通过主模型中的getData方法。实现对外部数据的读取，在算法的主模型GpModel类中，设计了一个方法getData()，该方法实现从数据库中读取数据，并且在模型的初始化方法init()中调用，从而使得算法模型与外部数据关联。如果要使用系统应用于其他领域的建模，只需要重写getData()方法。

2.3并行算法设计

由于我们的算法需要大量的运算，通常群体的大小在几百以上，进化的代数也在几百以上，这仅是小规模的运算。因此，从性能上考虑，充分利用CPU以及多核，将能够提高算法的运行效率。基于以上考虑，我们在算法流程的核心计算环节,将适应度值的计算、两个个体的交叉操作、个体的变异操作、个体的复制操作都从线程的粒度来进行，从而使得算法能够充分利用多处理器、多核来进行计算。

算法的并行流程如下：

begin

(1)initialization

产生一个初始群体

(2)whilerunningdo

(2.1) 并行评估整个群体的适应度值

(2.2) 判断是否已经达到搜索终止条件

(2.3) 并行进行遗传算子的操作

选择父代

根据随机概率进行交叉操作、复制操作和变异操作

//this.fileout();

//保存排序之前的数据

(2.4) 子代取代父代，形成新一代个体

endwhile

end

算法采用线程的方式来进行并行计算,使得多计算资源下解决问题的耗时少于单个计算资源下的耗时，因此提高了计算机系统的处理能力和计算速度，与此同时算法的效率大为提升。基于实际的运行效果可以看出，CPU多核运行是明显的，并且还没有达到饱和运行的状态。

2.4算法主程序设计

系统的主程序是GPMainFrame.java，这个类也是系统的主界面。在这个类中定义了遗传规划模型GpModel.java的一个实例，从而进行基于遗传规划的算法操作。

算法主程序GpModel.java中进行算法进化的主流程代码如下：

publicvoidevolution() {

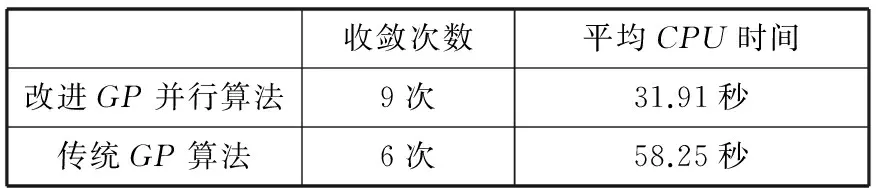
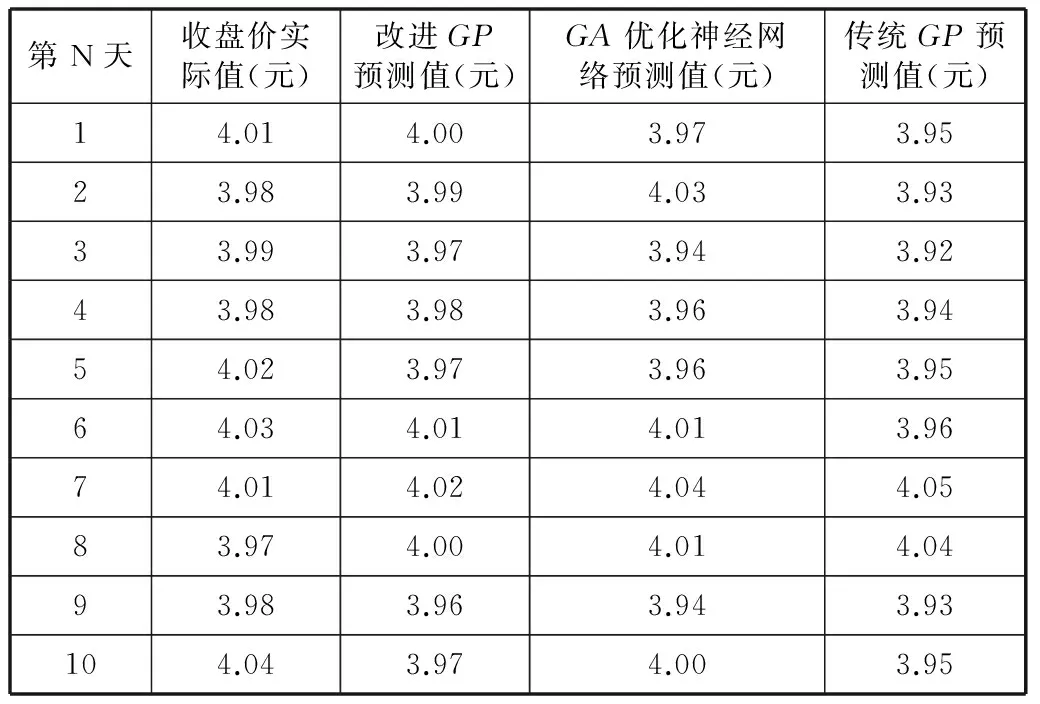
while(round

//操作界面有一个按钮，用来设置stop标志位

round++;

this.calculateFitness();//计算群体适应值，是并行计算

this.sortPopulation();

//排序

this.fileout();

//保存数据

if(this.achieveGoal())stop=true;

//如果达到目标要求，则进化结束

this.resetNextGen();

//初始化下一代个体

this.operator();

//进行遗传操作，完成一整代个体的更新

this.updateGeneration();

//下一代群体替代现有群体

}

}

3　算法实现

从功能的角度,要实现基于遗传规划的时间序列自适应建模算法，需要实现以下几个方面的算法：

(1) 数符号集与终端节点集的表达。系统需要定义好通用的数学表达式中的函数符号集、常数和变量集。除此以外，需要留有用户自定义变量集的接口，比如用户需定义n个变量，那么，系统能够很方便地实现具有n个变量的数学表达式的生成与进化。

(2) 模型个体的编码与解码。模型个体是由二叉树结构组成，在生成模型个体的时候，直接以二叉树结构来表示，而解码则是通过遍历将二叉树个体以字符串方式，按照通常数学表达式的语法来输出。

(3) 遗传规划算法的进化。实现模型个体的适应值评价、各遗传算子(复制、交叉和变异)的操作。

(4) 基本的算法控制界面。包括算法进化的开始、暂停进化和输出算法当前搜索的结果。算法进化的开始包括群体的初始化、进化循环启动功能；暂停进化主要是将进化循环条件置为false；当前结果的输出则是以文本的方式展示当前群体。

(5) 算法与模拟系统的数据接口。系统能够读取数据库中设定的数据，然后根据算法来完成建模。

我们的主要任务是实现算法的过程，不需要复杂的操作界面。由于基于文本的命令行界面，需要操作者掌握很多复杂的命令语句与参数，非计算机专业的使用者很难接受这种使用起来不直观的界面。随着人际交互技术的日益发展，界面友好的图形用户接口(GUI)越来越受到大家欢迎。因此，当前为算法过程的监控和实现设计了一个简单的图形用户界面。在界面中左侧有“开始”、“刷新”、“继续”和“暂停”四个按钮，右侧是一个显示算法演化过程中生成的模型情况的文本框。其中“开始”按钮用于启动建模算法，“刷新”按钮则将在界面的右边的文本框中添加当前的模型进化情况，“暂停”按钮则可以中止当前的算法循环，“继续”按钮可以恢复由于“暂停”按钮所中止的循环。

算法的软件包如图3所示。

图3　算法软件包

4　应用研究

4.1样本数据

由于算法的灵活性，我们可以对任意一只股票的每日收盘价在任意区段内的时间序列进行建模。使用CSMAR数据库查询系统，本文选取了中信银行(代码601998)从2011年1月4日至2011年12月30日区间的股票收盘价作为建模的样本数据,共234个工作日数据,选取前224个收盘价作为训练样本,通过分析这些历史数据建立遗传规划模型,然后预测后10天的收盘价。

4.2参数选择

算法的基本参数设置如表1所示。

表1　GP算法基本参数

为了保证模型的复杂度，避免群体中产生大量的Xt-1及类似的个体，我们在初始群体生成时人为地增加了函数节点产生的概率，并且随着个体生成时二叉树的层级的增加使用线性递减函数来降低函数节点的生成概率。

4.3结果分析

一般的股票价格预测模型需要事先设定具体的函数形式及具备一些假设前提条件，而遗传规划方法从数据出发，无需对初始数据进行预处理,能自动生成并寻找函数关系。将所确定的模型用简单明了的结构形式显式表达，具有很强的解释性，在对输入输出数据进行无需大量预处理的情况下，即能准确找到适合数据所呈现的规律的模型。这里所说的无需大量预处理即是无需对输入输出数据进行归一化和平稳化处理。表2列出了经10次运算后此支股票价格自适应建模算法得到适应度最好的模型。

表2　选取最优模型

对表2模型进行简化，得到的模型如下：

GP模型：Xt-1-0.0017×Xt-4+0.0003×Xt-10

为了讨论上述模型的合理性，我们应用理论分析的方法，对该时间序列建立经遗传算法(GA)优化的神经网络模型以及传统GP模型，以评价算法的可行性。

分别用本文改进的GP模型与文献[6]中提出的GA优化的神经网络方法以及传统GP算法3个不同的算法对2011年12月16日至2011年12月30日共10个工作日数据进行预测，其中对改进前后的GP算法各运行10次，分析运算性能如表3所示。

表3　运算性能比较

从表3可以看出，相对传统GP算法，经改进的GP并行算法收敛次数较多，且平均CPU耗时较少。

三种方法的实际预测结果如表4和图4所示。

表4　实际值与各模型预测值比较

图4　各模型预测效果图

计算各个模型预测值与实际值的相对误差如表5所示。

表5　各模型相对误差比较

由表5可以看出，GP模型中预测值的相对误差普遍较低，最小是0.00%，预测值均在实际值附近浮动,GA优化神经网络次之，传统GP算法模型中的相对误差较大。

为了更加全面地描述三个不同模型对股票价格的预测效果,本文采用平均绝对百分比误差(MAPE) 和均方根误差(RMSE) 两个指标来衡量模型预测效果的好坏(第一个指标是相对指标,第二个指标是绝对指标)。两个评价指标的定义分别为:

表6　各模型预测效果比较

从表6可以看出，无论是MAPE还是RMSE,改进遗传规划模型的预测误差都小于GA优化神经网络模型和传统GP模型，表明改进遗传规划方法预测效果优于另外两种模型，而GA优化神经网络模型的预测效果又优于传统GP模型。

进一步分析GP模型的结构：Xt-1-0.0017×Xt-4+ 0.0003×Xt-10，包含元素Xt-1，Xt-4，Xt-10，分别代表N天前的收盘价。这说明第t-1天，t-4天，和t-10天对第t天股票价格的关联和影响比较大，即是说股票价格的历史数据对未来的价格产生着一定程度影响，股票价格并不完全是随机的。另一方面，遗传规划自适应建模的结果中含有Xt-10元素，证明遗传规划方法具有较强的自适应搜索能力，可以准确地找出影响股票价格变化的因素。

5　结　语

本文通过Java实现的遗传规划并行算法具有强大的启发式搜索寻优能力。从运行过程看到，算法具有较快的运算速度和结构逼近性能，证明该算法在处理股票价格数据这种非线性时间序列预测方面具有较好的应用价值。在股票预测领域运用遗传规划方法的自适应搜索特性建模，能很快找到影响股票价格变化的影响因子，提高预测的精度，从另一个角度证实了遗传规划的自适应建模在预测领域的优越性。而且在处理历史数据中，采用遗传规划进行数据拟合时，不需要预先确定方程的结构形式，不需对数据进行预处理，大大减轻了我们在数据处理方面的工作量。相比神经网络的黑箱方法，GP方法建模结果具有多样性，可以比较容易且直观地表达并分析被预测系统的输入与输出之间的联系。从预测结果还可以看出股票市场的未来价格变化并不能认为是完全随机的，其有受到过去一段时间历史价格的影响。因此，投资者在股票市场投资时，把过去的价格变化因素考虑在内，有助于股票投资者在一定程度上做出正确的决策。

[1]KhasheiMehdi,RafieiFarimahMokhatab,BijariMehdi.HybridFuzzyAuto-RegressiveIntegratedMovingAverageModelforForecastingtheForeignExchangeMarkets[J].InternationalJournalofComputationalIntelligenceSystems,2013,6(5):954-968.

[2]SunBin,LiTieke.ForecastingandIdentificationofStockMarketbasedonModifiedRBFNeuralNetwork[C]//Proceedingsof2010IEEEthe17thInternationalConferenceonIndustrialEngineeringandEngineeringManagement,Xiamen,IEEE,2010(1):424-427.

[3] 尚朝辉，甄九州.基于遗传编程的技术分析在股票市场预测中的建模与应用[J].首都经济贸易大学学报，2014,16(2):28-35.

[4]KazemAhmad,SharifiEbrahim,HussainFarookhKhadeer.Supportvectorregressionwithchaos-basedfireflyalgorithmforstockmarketpriceforecasting[J].AppliedSoftComputing，2013,13(2):947-958.

[5] 肖菁，潘中亮.股票价格短期预测的LM遗传神经网络算法[J].计算机应用2012,32(S1)：144-146.

[6]MirchandaniBhisham,ShahCinjal,NagarshethKaushal.StockMarketTrendPredictionMarquardtNeuralNetworkOptimizedbyGeneticAlgorithm[C]//Phuket：4thInternationalConferenceonSoftwareTechnologyandEngineering,2012： 521-527.

[7] 王宇平.进化计算的理论和方法[M].北京：科学出版社，2011.

[8] 王璐.遗传算法与遗传规划的对比性研究[D].吉林：吉林大学，2011.

[9] 黄安强，李梦，杨丰梅.基于改进遗传规划算法的非线性集成预测新方法[J].系统科学与数学,2013，33(11)：1332-1344.

[10] 王璞.基于遗传规划的分类算法研究[D].合肥:中国科学技术大学,2013.

[11] 李擎,张超,徐银梅,等.基于专用遗传算法和改进粒子群算法的移动机器人路径规划[C]//安徽：第三十一届中国控制会议论文集D卷，2012：830-838.

[12] 林龄，潘峰.一种基于遗传规划的多特征图像排序算法[J].计算机应用与软件，2013,30(12)：190-193.

[13] 王安华.遗传规划在非复杂业务流程挖掘中的应用研究[D].上海:复旦大学,2010.

[14]CaySHorstmann,GaryComell.JAVA核心技术(卷1)[M].北京：机械工业出版社,2008.

IMPLEMENTINGJAVAINGENETICPROGRAMMINGADAPTIVEMODELLINGANDITSAPPLICATIONINSTOCKPRICEPREDICTION

GeZhiyuanChenHuitao

(School of Economics and Management,Beijing University of Technology,Beijing 100124,China)

Aimingatthewaytocombinethegeneticprogrammingmethodwithtimeserieseffectively,webuiltthegeneticprogramming-basedadaptivetimeseriesmodel,andimplementeditbyJavalanguageassistedalgorithm.Comparedwithpreviousgeneticprogrammingalgorithm,itusestheaveragevaluemethodtoimprovethegenerationmannerofinitialpopulation,makesthemutationprobabilitydecreasealongwiththeincreaseofevolutionalgebra.Moreover,theideaofparallelcomputingisintroduced,inthecorepartofthealgorithm,thecalculationoffitnessvalue,theoperationsofindividualcopy,thecrossoverandthemutationarecarriedoutfromthethreadgranularity.Basedontheactualoperationresults,theCPUoperatesclearlyinmulti-coremode,thealgorithmcantakefulladvantagesofmulti-processorandmulti-coreincomputationandthisimprovestheefficiencyofoperation.ApplyingthegeneticprogrammingmodeltothepredictionofstockspricesinChina’ssecuritiesmarket,wecomparedthepredictionresultswiththatoftheartificialneuralnetworkoptimisedbygeneticalgorithmandthetraditionalgeneticprogramming,resultsshowedthatthepredictionprecisionoftheimprovedgeneticprogrammingwashigher,andcouldmoreintuitivelyexpresstherelationshipbetweeninputandoutput.

GeneticprogrammingTimeseriesAdaptivemodellingStockpricePrediction

2014-08-13。葛志远，副教授，主研领域：Web技术，管理模型，遗传规划。陈会涛，硕士生。

TP311.1

ADOI:10.3969/j.issn.1000-386x.2016.03.027