浅谈高中数学不等式的恒成立问题
◇ 山东 余尚创
(作者单位:山东省淄博市高青县第一中学)
浅谈高中数学不等式的恒成立问题
◇山东余尚创
不等式恒成立问题是高考命题的热点之一,它涉及的知识面广、解法灵活多样,是学生学习中的难点.下面给出解答此类问题的几种常用方法并举例分析.
1 函数性质法
利用函数性质解不等式恒成立问题,首先要了解函数具有哪些性质,要灵活掌握函数的定义域、值域、单调性、奇偶性、周期性等知识,其中最常用的是函数的单调性.以下根据不同函数类型的单调性,对不等式恒成立问题进行求解.
1.1一次函数型
对于一次函数f(x)=kx+b(k≠0),若f(x)在[m,n]内恒有f(x)>0,则根据函数图象或一次函数的单调性:当k>0时,f(x) 在[m,n]内为增函数,当k<0时,f(x) 在[m,n]内为减函数,可得


分析在不等式中出现了2个字母x和a,首先应该在2个字母中确定一个字母为变量,另一个字母为常数.若将a视作自变量,则不等式x2+ax+1>a+2x恒成立即可转化为在[-2,2]内关于a的一次函数大于0恒成立的问题.
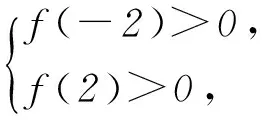
x∈(-∞,-1)∪(3,+∞).
1.2二次函数型
对于二次函数恒成立的问题,又分为:
1) 对于二次函数f(x)=ax2+bx+c(a≠0,x∈R),若f(x)>0恒成立,则有a>0且Δ<0.
2) 在指定区间内,二次函数恒成立的问题,可以利用根与系数的关系或根的分布来求解.

分析题目中要证明f(x)≥a恒成立,将a移到不等号的左边,把原问题转变成求二次函数在区间[-1,+∞)内恒大于0.
解设F(x)=f(x)-a=x2-2ax+2-a.
当Δ=4(a-1)(a+2)<0,即-2 当Δ=4(a-1)(a+2)≥0时,由图1可得 图1 即 解得-3≤a≤-2. 综上可得,a的取值范围为[-3,1). 针对含有2个变量的等式(或不等式)的恒成立问题,若其中一个变量的范围已知,另一个变量为所求.可以利用分离参数法,把等式(或不等式)的2个变量通过恒等变形分别置于等号(或不等号)的两边,通过求最值的方法来解这类恒成立问题. 分析在不等式中含有2个变量a及x,其中x的范围已知(x∈R),求a的取值范围.所以可以考虑把不等式进行变形,将a、x分别置于不等式两边,进行变量分离. 解原不等式可化为4sinx+cos2x<-a+5,所以本题就转化成求-a+5>(4sinx+cos2x)max,求f(x)=4sinx+cos2x的最大值即可. 因为f(x)=4sinx+cos2x=-2sin2x+4sinx+1=-2(sinx-1)2+3≤3,所以-a+5>3即a<2. 针对较容易画出图象的函数,我们可以采取数形结合法来进行解答. 图2 分析若将不等号两边分别设成2个函数,则左边为二次函数,图象是抛物线,右边为常见的对数函数,故可以通过图象求解. 图3 解设f(x)=(x-1)2,g(x)=logax,则f(x)的图象如图3所示的抛物线,要使对∀x∈(1,2),f(x) 对于比较容易求出最值的函数,解答这类函数恒成立问题时,可把最值求出来,若函数带有参数,进一步求参数的范围即可. 当-a 所以函数的单调递增区间为(-∞,-a),(a/3,+∞).单调递减区间为(-a, a/3). 当a∈[3,6],a/3∈[1,2],-a≤-3. 又因为x∈[-2,2], 所以fmax(x)=max{f(-2), f(2)},而f(-2)=-8+4a+2a2+m,f(2)=8+4a-2a2+m.由f(-2)-f(2)=-16+4a2>0,得fmax(x)=f(-2)=-8+4a+2a2+m.要使不等式f(x)≤1在x∈[-2,2]上恒成立,只需fmax(x)=f(-2)=-8+4a+2a2+m≤1,即m≤9-4a-2a2在a∈[3,6] 上恒成立.g(a)=9-4a-2a2在a∈[3,6]的最小值为-87,所以m≤-87. 不等式的恒成立问题涉及的知识点比较广,类型比较多,解题方法也很灵活,此类问题经常与参数的取值范围联系在一起,并结合函数的单调性、极值、最值等性质来解答,这就需要同学们灵活掌握恒成立问题各种类型的解答方法,解答时注意结合相关函数的性质,找到题目考察的知识点,进而从容应对考题. (作者单位:山东省淄博市高青县第一中学)

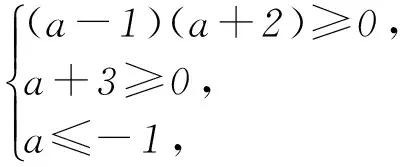

2 分离参数法




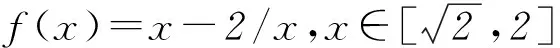

3 数形结合法


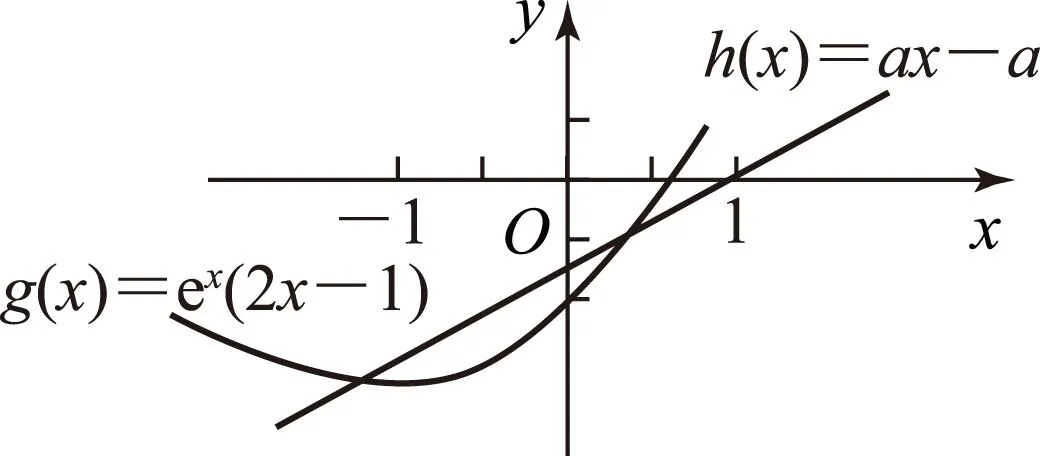


4 最值法




