页岩气新井压裂规模优化设计
裴艳丽,姜汉桥,李俊键,刘传斌,周赫,余曦
(1.中国石油大学石油工程教育部重点实验室,北京 102249;2.中联煤层气有限责任公司北京研究中心,北京 100011)
页岩气新井压裂规模优化设计
裴艳丽1,姜汉桥1,李俊键1,刘传斌1,周赫1,余曦2
(1.中国石油大学石油工程教育部重点实验室,北京 102249;2.中联煤层气有限责任公司北京研究中心,北京 100011)
由于页岩气藏的渗透率极低,一般小于0.1×10-3μm2,对其实施多级分簇大规模体积压裂是目前改善储层导流能力、提高储层产能的关键技术。以涪陵页岩气田某区块为例,基于线网模型,文中提出了一套系统的页岩气藏新井压裂规模优化设计方法。根据老井压裂及试产数据,利用主成分分析法,筛选影响气井产能的关键压裂参数(压裂级数、裂缝导流能力和缝网带长)。采用响应面方法对区块新钻井的压裂施工进行优化设计,得到最佳新井压裂参数:压裂级数3,缝网带长120 m,裂缝导流能力45×10-3μm2·m。通过对老井压裂参数的统计分析,优化设计新井的体积压裂规模,可以最大程度发挥体积压裂的增产效果,实现页岩气藏的高效开发。
页岩气;新井压裂规模;主成分分析;响应面方法
页岩气是一种以游离态或吸附态赋存于泥页岩中的非常规天然气[1],而体积压裂技术是目前开发页岩气藏的主要增产技术[2-3]。借助油藏数值模拟软件设计页岩气藏开发方案时,必须考虑井网中新井的体积压裂规模。笔者以涪陵页岩气田某区块为例,采用线网模型表征复杂裂缝网络的体积压裂参数,对初探井的压裂参数进行主成分分析筛选关键因素,并采用响应面方法进行压裂参数优化,形成了一整套系统的页岩气藏新井压裂规模优化设计方法。
1 体积压裂参数表征
目前,关于体积压裂缝网的描述主要包括离散缝网模型(DFN)、水力缝网模型(HFN,又称线网模型)、非常规缝网模型(UFM)及缝网双重介质模型(FNDP)。前2种模型忽略天然裂缝的影响[4-6],分别采用椭球体和椭柱体描述对称、规则的网状裂缝扩展;后2种模型考虑天然裂缝的影响[7-8],可以模拟非对称、不规则的缝网系统。实际上,天然裂缝的空间分布存在很大的随机性,难以在数值模拟软件中精确描述。目前多采用“双重介质模型表征天然裂缝+线网模型表征人工裂缝”的方法模拟。
对于页岩体积压裂,储层改造体积是描述压裂效果的关键参数。Warpinski等[9]提出用三维箱体体积近似代替缝网体积,即

式中:SRV为储层改造体积,m3;L为缝网长度,m;W为缝网宽度,m;H为缝高,m。
考虑第i级体积压裂缝网,则第i级次裂缝延伸长度定义为第i级缝网带宽Wi,第i级主裂缝延伸长度定义为第i级缝网带长Li,第i级裂缝高度定义为第i级缝网高度Hi。除考虑上述描述缝网的特殊参数外,还应包括常规储层压裂的相关参数,如裂缝开度、裂缝渗透率及裂缝导流能力等。概括来讲,影响页岩气井产能的因素分地质因素和施工因素2类。其中:地质因素指岩石孔隙度和渗透率;施工因素指压裂施工的参数,裂缝导流能力囊括了裂缝开度与裂缝渗透率的信息,因此施工因素简化为裂缝导流能力、压裂体积、缝网带长、缝网带宽。
2 模型建立
以涪陵页岩气田某区块为例,工区具体参数见表1。该区块共有5口生产井,其中4口井进行了压裂试采。统计4口试采井的微地震检测数据,用于描述人工裂缝的发生、发展和空间分布。

表1 现场基础资料
数值模拟采用角点网格,I,J,K方向的网格总数为61×21×10,各方向单元网格边长为50 m×50 m×8 m。压裂水平井长度取1 200 m,压裂级数控制在3左右。以简单的双重介质模型为基础,采用线网模型模拟压裂形成的复杂裂缝网络。通过在平面上改变加密网格的渗透率,实现椭柱体的裂缝分布。
3 新井压裂规模设计
3.1主成分分析法
由于难以定性描述各个地质因素和施工因素之间的独立性,这里采用主成分分析法定量呈现各要素的相关性。数值模拟研究表明,水平井端部裂缝控制的泄油面积大,受缝间干扰程度小,单级缝网产能沿水平井由端部到根部逐渐降低。这里忽略压裂发生位置不同引起的产能差异,认为理想情况下各级压裂对应相同的产气量。各试采井的产能影响参数见表2。
主成分分析的步骤如下:
1)参数标准化。对于各类体积压裂参数,数量级差别显著。为了保证主成分分析结果的合理性,首先将各列参数标准化。标准化的方法是用各样本数据减去列均值,然后除以列标准差。

表2 体积压裂参数统计
2)主成分提取。分别定义标准化的裂缝导流能力、压裂体积、缝网带长、缝网带宽、孔隙度及渗透率为影响因子X1—X6,求取其对应的特征值及特征向量,其中特征向量Z1—Z6即为求取的主成分。
3)显著性分析。选取累积贡献率达到98%的主成分,即Z1,Z2,Z3,Z4。一般,当P值大于0.050 0时,说明该主成分影响程度不显著。只有Z4的P值(0.281 5)大于0.050 0,去掉显著性较差的因子Z4,得到最终的3个主成分Z1,Z2,Z3。
4)逐步回归。去掉不显著的主成分,将主成分Z1,Z2,Z3重新回归。根据逐步回归结果,标准化产量Y的线性回归方程为

从而得到Y与标准化影响因子X1—X6的关系式:
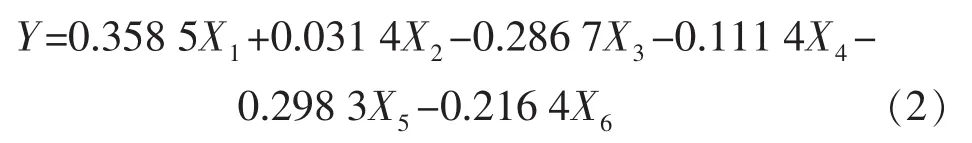
式(2)表明,裂缝导流能力和缝网带长对气井产能的影响较大,而缝网带宽和压裂体积的影响较小。另外,在多级分簇大规模体积压裂中,压裂级数也应该作为一个重要因素加以考虑。李宪文等[8-9]的研究表明,相同储层改造体积下,压裂级数越多,缝网带长越小,其开发效果次于级数较少的压裂方式。由于5口初探井的压裂级数均为3,在主成分分析部分无法体现压裂级数的影响,但在响应面分析中必须加以考虑。
3.2响应面方法
响应面方法(RSM)是一种经验统计建模技术,是处理多因素系统的有效工具。它通过响应面设计来安排实验,再对实验结果进行回归分析,建立响应变量与各因子间的数学模型,从而确定各因子对响应的影响程度,以求优化该响应、确定最优工艺条件或达到指定响应值要求的因子空间。相比于正交实验设计法,响应面方法具有实验周期短、回归方程精度高和能研究各因素交互作用的优点[10]。
3.2.1体积压裂实验方案
根据Box-Behnken Design(BBD)实验设计原理,选取3个对气井产能影响较大的因素——压裂级数(A)、缝网带长(B)和裂缝导流能力(C),采用Design-Expert软件对新井压裂参数进行优化设计。BBD实验设计方案见表3。
3.2.2响应面分析结果
根据数值模拟实验结果,建立的数学模型为

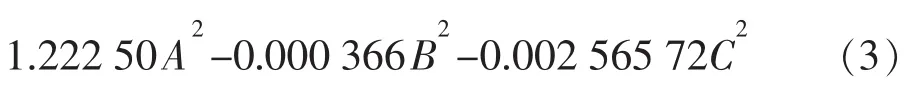
式中:R为采出程度。

表3 BBD实验设计方案
从统计分析结果来看,整体模型的P值小于0.0001,表明该回归模型高度显著(见表4)。就单项指标而言,P值越大,影响程度越小。在所选取的各因素水平范围内,按照对采出程度的影响程度排序为:压裂级数>裂缝导流能力>缝网带长(“>”表示“高于”)。

表4 体积压裂参数数学统计分析结果
3.2.3各因素交互影响
图1直观地反映了各因素交互作用对响应值的影响。对比3组图可以看出:压裂级数对采出程度的影响最为显著,表现为曲线较陡;裂缝导流能力和缝网带长次之,表现为曲线较为平滑。

图1 各因素交互作用对响应值的影响
3.2.4压裂参数优化结果
根据各压裂参数影响以及采出程度响应面,优选得到3种方案。考虑到压裂技术的局限以及现场施工的时耗,对压裂级数按照四舍五入取整处理(见表5)。

表5 调整的压裂规模优化设计方案
数值模拟结果表明,3种优化方案的最优采出程度和检验采出程度之间的误差很小。因此,响应面方法求得的采出程度回归方程是可靠的,能够用于方案的优化。考虑页岩开采的经济性,压裂级数与缝网带长和经济成本息息相关,在采出程度相差不大的情况下,最终选择方案2作为新井压裂的最优参数设计。
4 结论
1)本文在数值模拟中采用“双重介质模型表征天然裂缝+线网模型表征人工裂缝”的方法模拟。
2)将影响页岩气藏开发效果的参数归结为地质因素和施工因素2大类。地质因素指岩石孔隙度和渗透率;施工因素指裂缝导流能力、压裂体积、缝网带长、缝网带宽。
3)对于研究区块而言,利用主成分分析法筛选影响气井产能的3大因素为压裂级数、裂缝导流能力和缝网带长。优化设计3类参数,可以预测新井压裂规模,为页岩区块新钻井的压裂施工提供依据。
4)采用Design-Expert软件,基于BBD原理设计了体积压裂方案。结果表明,压裂级数对采出程度的影响最为显著,裂缝导流能力和缝网带长次之。通过响应面方法优化,得到该区块最佳新井压裂参数:压裂级数3,缝网带长120 m,裂缝导流能力45×10-3μm2·m。
[1]张金川,金之钧,袁明生.页岩气成藏机理和分布[J].天然气工业,2004,24(7):15-18.
[2]赵崇镇.新场气田须五致密气藏缝网压裂技术[J].石油钻探技术,2015,43(6):70-75.
[3]周德华,焦方正,贾长贵,等.JY1HF页岩气水平井大型分段压裂技术[J].石油钻探技术,2014,42(1):75-80.
[4]MEYER B R.Three-dimensional hydraulic fracturing simulation on personalcomputers:theoryandcomparisonstudies[R].SPE19329,1989.
[5]XU W,LE CALVEZ J H,THIERCELIN M J.Characterization of hydraulically-inducedfracturenetworkusingtreatmentand microseismic data in a tight-gas sand formation:a geomechanical approach[R].SPE 125237,2009.
[6]XU W,THIERCELIN M J,WALTON I C.Characterization of hydraulically-induced shale fracture network using an analytical/semianalytical model[R].SPE 124697,2009.
[7]CIPOLLA C L,WILLIAMS M J,WENG X,et al.Hydraulic fracture monitoring to reservoir simulation:maximizing value[R].SPE 133877,2010.
[8]李宪文,樊凤玲,李晓慧,等.体积压裂缝网系统模拟及缝网形态优化研究[J].西安石油大学学报(自然科学版),2014,29(1):71-75.
[9]WARPINSKI N R,MAYERHOFER M J,VINCENT M C,et al. Stimulating unconventional reservoirs:maximizing network growth while optimizing fracture conductivity[R].SPE 114173,2008.
[10]隋允康,宇慧平.响应面方法的改进及其对工程优化的应用[M].北京:科学出版社,2011:4-18.
(编辑赵卫红)
Fracturing scale optimization design for new shale gas well
PEI Yanli1,JIANG Hanqiao1,LI Junjian1,LIU Chuanbin1,ZHOU He1,YU Xi2
(1.MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.Beijing Research Center,China United Coalbed Methane Co.Ltd.,Beijing 100011,China)
Due to the low permeability of shale gas reservoir,generally smaller than 0.1×10-3μm2,multistage clustering volume fracturing is a key technique to improve flow conductivity and reservoir productivity.According to the basic information from a block in Fuling shale gas field,a set of systematic fracturing scale optimization design method for new drilling wells was proposed based on wire-mesh model.Principle component analysis was conducted on fracturing and production data of old wells to screen the most influential SRV parameters(number of fracturing stages,fracture conductivity,and fracture network band length).Response surface method was then applied to optimize key fracturing parameters for new drilling wells,which indicated the optimum fracturing parameters should be fracturing stages of 3,fracture network band length of 120 m and fracture conductivity of 45×10-3μm2·m. Through the statistical analysis of old shale gas wells,it is possible to predict the stimulated reservoir volume(SRV)scale for new drilling wells.This method will maximize the SRV yield-increasing effect and achieve efficient development of shale gas reservoir.
shale gas;new well fracturing scale;principal component analysis;response surface method
国家重点基础研究发展计划(973计划)项目“页岩气气藏工程方法基础研究”(2013CB228005)、“致密油高效开发油藏工程理论与方法研究”(2015CB250905);中国石油大学(北京)引进人才科研启动基金“复杂缝网页岩气藏离散介质数值模拟方法”(2462013YJRC012)
TE254
A
10.6056/dkyqt201602030
2015-08-23;改回日期:2016-01-07。
裴艳丽,女,1991年生,在读硕士研究生,主要从事油气藏开发方面的研究。E-mail:peiyanlipyl@163.com。
引用格式:裴艳丽,姜汉桥,李俊键,等.页岩气新井压裂规模优化设计[J].断块油气田,2016,23(2):265-268. PEI Yanli,JIANG Hanqiao,LI Junjian,et al.Fracturing scale optimization design for new shale gas well[J].Fault-Block Oil&Gas Field,2016,23(2):265-268.

