有轨电车二系垂向悬挂系统阻尼比优化

于曰伟，周长城，赵雷雷

(山东理工大学 交通与车辆工程学院，山东 淄博255049)



有轨电车二系垂向悬挂系统阻尼比优化

于曰伟，周长城，赵雷雷

(山东理工大学 交通与车辆工程学院，山东 淄博255049)

针对有轨电车二系垂向悬挂系统中存在的阻尼匹配问题，根据1/4车体三自由度垂向振动模型，利用MATLAB/Simulink建立了二系垂向悬挂系统阻尼比优化设计仿真模型；以人体振动舒适性最佳为目标，建立了二系垂向悬挂系统阻尼比优化设计数学模型.在此基础上，以轨道高低不平顺作为输入激励，以二系悬挂垂向行程及一系悬挂垂向动作用力为约束条件，创建了二系垂向悬挂系统阻尼比优化设计方法.通过实例对阻尼比进行了优化设计，可知阻尼比的优化设计值能够显著提高有轨电车的乘坐舒适性，表明所建立的有轨电车二系垂向悬挂系统阻尼比的优化设计方法是正确的，为二系垂向悬挂系统阻尼匹配减振器设计奠定了重要理论基础.

有轨电车；二系垂向悬挂系统；阻尼比优化；三自由度垂向振动模型

有轨电车因具有能耗低、环保、灵活性强等优点已成为公共交通发展的新趋势.二系垂向悬挂系统作为有轨电车的重要组成部分，其阻尼匹配对有轨电车的运行平稳性和安全性具有重要影响[1-2].然而，由于受轨道车辆悬挂系统最优阻尼匹配理论的制约，目前国内外对于有轨电车二系垂向悬挂系统阻尼比的设计，大都是根据经验在可行性设计区间(0.2～0.45)选择某一阻尼比值[3-5]，然后利用多体动力学软件SIMPACK或ADAMS/Rail通过实体建模仿真，根据主观和客观加以综合判断，最终确定某设计值.虽然利用该方法所得到的二系垂向悬挂系统的阻尼比值，可使车辆满足当前行驶工况的要求，然而并非是有轨电车二系垂向悬挂系统的最佳阻尼匹配值.随着有轨电车的快速发展，人们对其乘坐舒适性和运行安全性提出了更高的设计要求，目前二系垂向悬挂系统阻尼比的设计方法不能给出具有指导意义的创新理论，不能满足有轨电车发展及其悬挂系统设计的要求.

目前已有许多国内外学者对轨道车辆二系垂向悬挂系统进行了大量的研究，但这些研究主要是针对减振器阻尼系数进行的，主要采用的方法有控制设计理论法、智能优化设计法和建模仿真优化法.例如，文献[6-7]分别利用H∞和分散控制技术对轨道车辆的二系垂向悬挂系统进行研究，给出了基于控制设计理论的二系垂向悬挂系统减振器的最佳阻尼系数优化设计值；文献[8-13]分别利用遗传算法，神经网络算法，全局优化算法，稳健性设计，多目标优化方法等对轨道车辆悬挂系统进行优化设计，给出了基于智能优化方法的二系垂向悬挂系统减振器的最佳阻尼系数优化设计值；文献[14-15]分别利用ANSYS软件和MATLAB软件对轨道车辆悬挂系统进行优化设计，给出了基于建模仿真的二系垂向悬挂系统悬挂参数的优化设计值.虽然这些研究能够给出二系垂向悬挂系统减振器的最佳阻尼系数设计值，但这些研究所建立的振动模型或仿真模型中未考虑减振器端部连接结构的弹性作用，且未曾给出具有指导意义的二系垂向悬挂系统阻尼比的设计理论.因此，目前二系垂向悬挂系统阻尼比的设计方法，无法满足有轨电车二系垂向悬挂最佳阻尼匹配的要求.本文根据1/4车体三自由度垂向振动模型，通过车辆运行平稳性和安全性分析，对有轨电车二系垂向悬挂系统阻尼比进行研究，并结合实例，对二系垂向悬挂系统阻尼比进行优化设计及仿真验证.

1　1/4车体三自由度垂向振动模型

由于有轨电车对称于其纵轴线，且对于单节车体，其转向架系统的轮对、一系及二系悬挂前后、左右对称分布，故在分析二系垂向悬挂系统对车体频率响应和平稳性的影响时，可将有轨电车整体行驶振动模型简化为1/4车体三自由度垂向振动模型，如图1所示.其中，模型中考虑了减振器的端部连接刚度和一系悬挂橡胶弹簧的阻尼，坐标原点位于各自静平衡位置处.

图1　1/4车体三自由度垂向振动模型

图1中，m1为单个转向架构架质量的一半，K1、C1分别为每台转向架单侧一系悬挂橡胶弹簧的垂向等效刚度和垂向等效阻尼；m2为单节车体满载质量的1/4，K2为每台转向架单侧二系垂向悬挂弹簧的刚度，C2为每台转向架单侧二系垂向减振器的阻尼系数，Kd为每台转向架单侧二系垂向减振器的端部连接刚度；z1为转向架构架的垂向位移，zd为二系垂向减振器的活塞杆垂向位移，z2为车体的垂向位移，zv为轨道高低不平顺随机输入.

根据所建立的1/4车体三自由度垂向振动模型，在不计轮—轨耦合及减振器质量情况下，利用牛顿第二定律，建立车体垂向振动微分方程，即

(1)

同时，由于考虑了二系减振器端部连接结构的弹性作用，因此，根据减振器阻尼力与端部橡胶衬套弹性力平衡，可建立以下补充方程，即

(2)

利用车体垂向振动微分方程式(1)及二系减振器阻尼力与端部橡胶衬套弹性力平衡的补充方程式(2)，可对在轨道激励下的有轨电车行驶振动响应及二系垂向悬挂系统阻尼比的优化设计进行研究.

2　轨道高低不平顺激扰模型

2.1轨道高低不平顺

轨道高低不平顺是引起机车车辆产生垂向振动的主要原因.近年来，国内外对于轨道高低不平顺已进行了大量的研究，其中应用较为成熟、广泛的主要有美国六级轨道谱和德国高速轨道谱[16].由于美国六级轨道谱对低速轨道线路的拟合程度较高，因此，本文采用美国高低不平顺作为有轨电车垂向振动的轨道输入，其中，美国高低不平顺以空间频率形式表示的解析表达式为

(3)

式中:Sv(Ω)为轨道高低不平顺功率谱密度，Ω为轨道不平顺的空间频率;Av为轨道粗糙度系数，Ωc为截断空间频率;K为安全系数，取值范围为0.25～1.0，计算车辆响应时，一般取0.25.其中，各已知参数值如表1所示，美国高低不平顺轨道谱的功率谱密度随空间频率Ω变化的曲线，如图2所示.

表1美国高低不平顺参数值

参数线路等级1级2级3级4级5级6级Av/cm2·rad·m-11.21071.01810.68160.53760.20950.0339Ωc/rad·m-10.82450.82450.82450.82450.82450.8245最高运行速度/km·h-1货车16406496128176客车244896128144176

图2　美国高低不平顺功率谱密度随空间频率Ω的变化

2.2轨道高低不平顺时域样本的模拟合成

目前国内外对于轨道不平顺时域样本的模拟合成，主要采用的方法有二次滤波法、三角级数法、白噪声滤波法、以及基于功率谱密度采样的轨道不平顺数值模拟新方法等[16].本文采用对轨道线路拟合程度高且能够真实反映线路实际情况的基于功率谱密度采样的轨道不平顺数值模拟新方法对轨道高低不平顺时域样本进行合成，其中，所合成的有轨电车运行速度为70km/h时的轨道高低不平顺时域模拟序列及其功率谱密度曲线分别如图3、图4所示.

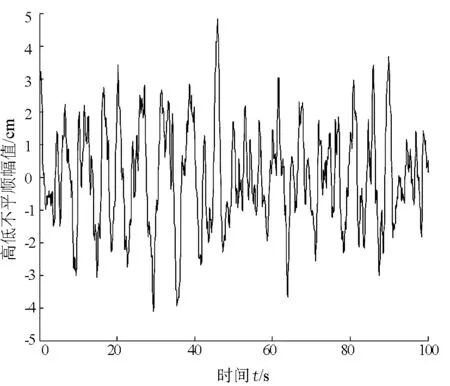
图3　轨道高低不平顺时域模拟序列

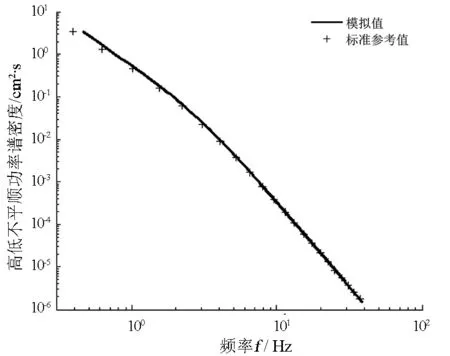
图4　轨道高低不平顺模拟值与标准参考值的比较

由图3和图4可以看出：轨道高低不平顺幅值在-4～+4cm范围内变化，且所合成的美国3级轨道高低不平顺的功率谱密度模拟值与标准参考值几乎完全一致.

3　二系垂向悬挂系统阻尼比优化

3.1舒适性评价指标

为了对有轨电车二系垂向悬挂系统阻尼比进行优化设计，首先必须明确人体振动舒适性评价指标.目前，国内外最常用的人体舒适性和健康评价指标为ISO2631标准[17]中规定的加权加速度均方根值，其中，考虑人体对不同频率及不同方向振动的敏感程度不同，分别对加速度进行频率加权和方向加权.由于本研究主要针对垂向振动对舒适性的影响进行评价，因此，仅计算垂向振动加权加速度均方根值.其中，在不同频率下的频率加权值w(f)的计算公式为

(4)

3.2阻尼比优化设计目标函数

根据每台转向架单侧二系垂向减振器的阻尼系数C2与悬挂系统参数及待优化设计阻尼比之间的关系，可得

(5)

式中，ξ2为二系垂向悬挂系统阻尼比.

(6)

3.3阻尼比优化设计约束条件

为了保证有轨电车行驶时具有良好的运行平稳性和安全性，在对其二系垂向悬挂系统阻尼比进行优化设计时，应满足以下约束条件：

(1)二系悬挂垂向行程

为了减小车辆高速运行过程中撞击限位的概率，使车辆具有良好的运行平稳性和安全性，二系悬挂垂向行程的均方根值σfd应限制在限位行程[fd]的1/3之内，这时悬挂击穿的概率小于0.135%，即

(7)

(2)一系悬挂垂向动作用力

为了使车轮不抬离轨道表面，以保障车辆的运行安全性，轮对所受一系悬挂垂向动作用力的均方根值σFd应小于静作用力的1/3，即

(8)

3.4有轨电车二系垂向悬挂系统阻尼比优化

(1)阻尼比优化设计仿真模型

为使有轨电车二系垂向悬挂系统的阻尼匹配达到最佳，需对该系统的阻尼比进行优化设计，建立待设计有轨电车二系垂向悬挂系统阻尼比的优化设计仿真模型.

根据所建立的车体垂向振动微分方程式(1)，式(2)及式(5)，利用MATLAB软件的Simulink工具箱，构建有轨电车二系垂向悬挂系统阻尼比优化设计仿真模型，如图5所示.

图5　有轨电车二系垂向悬挂系统阻尼比优化设计仿真模型

(2)二系垂向悬挂系统阻尼比优化设计

多岛遗传算法作为一种伪并行遗传算法可有效避免早熟和加快收敛速度，可以很好地在优化域中寻找全局最优解.为此，本文采用多岛遗传算法，利用MATLAB对有轨电车二系垂向悬挂系统阻尼比进行优化，优化设计流程图如图6所示，其中，参数设定如下：有轨电车二系垂向悬挂系统阻尼比的优化设计初始值ξ2=0，优化范围ξ2∈(0,0.5)；多岛遗传算法的子群规模为10，岛个数为10，进化代数为10，交叉概率为1，变异概率为0.01，迁移概率为0.01，迁移的间隔代数为5.

图6　优化设计流程图

根据所建立的有轨电车二系垂向悬挂系统阻尼比优化设计仿真模型，阻尼比优化设计目标函数式(6)及约束条件式(7)～(8)，以二系垂向悬挂系统阻尼比ξ2为设计变量，以美国轨道高低不平顺作为轨道输入激励，依据上述优化设计流程，利用所编写的优化设计程序求目标函数Jo(ξ2)的最小值，便可得到有轨电车二系垂向悬挂系统的最优阻尼比ξ2.

4　设计实例及分析

某有轨电车的最高运行速度v=70km/h，1/4单节车体满载质量m2=14 228kg，单个转向架构架质量的一半m1=1 400kg，每台转向架单侧一系悬挂橡胶弹簧的垂向等效刚度K1=4.96×106N/m、等效阻尼C1=9.36kN·s/m，每台转向架单侧二系垂向悬挂弹簧的刚度K2=5.94×105N/m，每台转向架单侧二系垂向减振器的端部连接等效刚度Kd=20×106N/m，每台转向架单侧二系垂向减振器的阻尼系数为C2，二系悬挂的垂向限位行程[fd]=35mm，对该有轨电车的二系垂向悬挂系统阻尼比进行优化设计.已知该有轨电车二系垂向悬挂系统阻尼比优化设计前的取值ξ2=0.35.

利用所建立的有轨电车二系垂向悬挂系统阻尼比的优化设计方法，对该车辆二系垂向悬挂系统的阻尼比进行优化设计，优化设计值和经验设计值的对比结果如表2所示.其中，该车辆优化设计前、后车体垂向振动加速度的时域信号及其功率谱密度曲线，分别如图7、图8所示；优化设计后的二系悬挂垂向行程和一系悬挂垂向动作用力随时间变化的曲线，分别如图9、图10所示.

表2阻尼比设计值对比结果

阻尼比设计参变量ξ2设计值经验设计0.35优化设计0.24

可知，阻尼比的优化设计值ξ2=0.24，在二系垂向悬挂系统阻尼比的可行性设计区间(0.2～0.45)范围内[3]，表明所设计的二系垂向悬挂系统最优阻尼比值是可靠的.

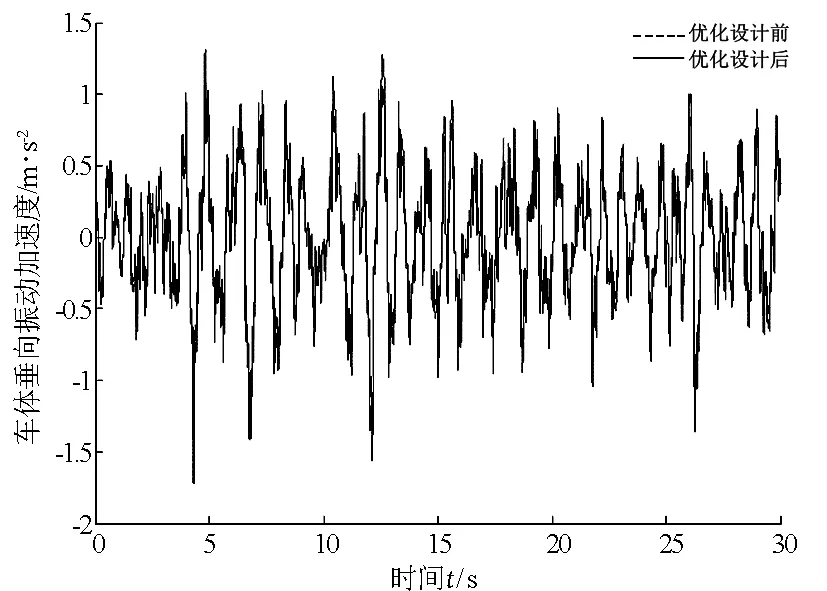
图7　车体垂向振动加速度时域信号

图8　车体垂向振动加速度功率谱密度曲线

分析图7和图8可知，有轨电车二系垂向悬挂系统阻尼比优化设计后，其车体垂向振动加速度和功率谱密度值比优化设计前有所降低.其中，优化设计前的车体垂向振动加权加速度均方根值为0.29m/s2，优化设计后的为0.24m/s2，舒适性提高了17.2%.对比可知，优化设计后车辆的乘坐舒适性得到了明显的提高.

由图9和图10可以看出，二系悬挂垂向行程在-25～+25mm范围内变化，一系悬挂垂向动作用力在-2.5×104～+2×104N范围内变化.其中，二系悬挂垂向行程的均方根值为6.9mm，一系悬挂垂向动作用力的均方根值为5.82×103N，均未超出约束条件的要求，表明所设计的二系垂向悬挂系统最优阻尼比值是可靠的.

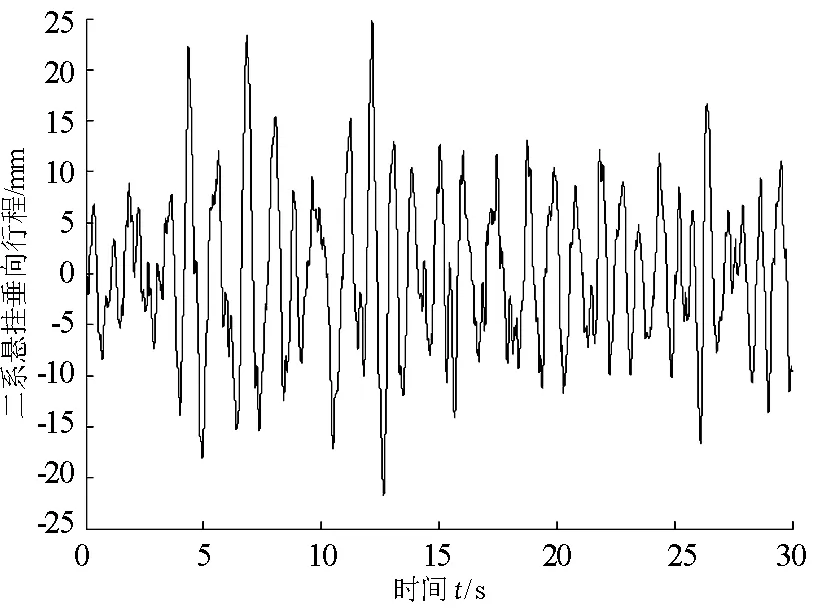
图9　二系悬挂垂向行程随时间变化

图10　一系悬挂垂向动作用力随时间变化

5　结束语

通过有轨电车二系垂向悬挂系统阻尼比优化方法的理论研究、实例设计及仿真验证，可知：根据1/4车体三自由度垂向振动模型，利用MATLAB/Simulink，可建立有轨电车二系垂向悬挂系统阻尼比优化设计仿真模型；利用有轨电车二系垂向悬挂系统阻尼比优化设计仿真模型，以人体振动舒适性最佳为目标，以轨道高低不平顺作为输入激励，以二系悬挂垂向行程及一系悬挂垂向动作用力为约束条件，可建立二系垂向悬挂系统阻尼比优化设计方法.实例设计及对比验证结果表明：所建立的有轨电车二系垂向悬挂系统阻尼比优化设计方法是正确的，能够显著改善有轨电车的乘坐舒适性，为未来有轨电车的提速及悬挂系统设计提供了重要理论基础，为常规行驶工况下的基于1/4车辆模型的有轨电车二系垂向悬挂系统阻尼比的优化设计提供了一种行之有效的指导方法.

[1]AucielloJ,MeliE,FalomiS,etal.Dynamicbehaviouroftramwayswithdifferentkindsofbogies[J].VehSystDyn, 2009, 47(7): 867-899.

[2] 孟宏, 翟婉明, 王开云. 二系悬挂对机车动力学性能的影响[J]. 铁道机车车辆, 2005, 25(5): 1-4.

[3] 杨国桢, 王福天. 机车车辆液压减振器[M]. 北京: 中国铁道出版社, 2003.

[4]EomBG,LeeHS.Assessmentofrunningsafetyofrailwayvehiclesusingmultibodydynamics[J].InternationalJournalofPrecisionEngineering&Manufacturing, 2010, 11(11):315-320.

[5]EichbergerA,HofmannG.TMPT:multi-bodypackageSIMPACK[J].VehSystDyn, 2007, 45(Suppl): 207-216.

[6]NguyenHC,SoneA,IbaD,etal.Designofpassivesuspensionsystemofrailwayvehiclesviacontroltheory[J].JournalofSystemDesignandDynamics, 2008, 2(2): 518-527.

[7]ZuoL,NayfehS.Designofpassivemechanicalsystemsviadecentralizedcontroltechniques[C]//43rdAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamics,andMaterialsConference.Denver:AmericanInstituteofAeronauticsandAstronautics, 2002: 1-9.

[8]MeiTX,GoodallRM.Useofmultiobjectivegeneticalgorithmstooptimizeinter-vehicleactivesuspensions[J].JournalofRailandRapidTransit, 2002, 216(1) :53-63.

[9]MastinuRM,GobbiM.Ontheoptimaldesignofrailwaypassengervehicles[J].JournalofRailandRapidTransit, 2001, 215(2): 111-124.

[10]KimYG,ParkCK,ParkTW.Designoptimizationforsuspensionsystemofhighspeedtrainusingneuralnetwork[J].JSMEInternationalJournalSeriesC, 2003, 46(2): 727-735.

[11]BatouA,SoizeC,ChoiCK,etal.Robustdesigninmultibodydynamics-applicationtovehicleride-comfortoptimization[J].ProcediaIUTAM, 2015, 13: 90-97.

[12]GeorgiouG,VerrosG,NatsiavasS.Multi-objectiveoptimizationofquarter-carmodelswithapassiveorsemi-activesuspensionSystem[J].VehSystDyn, 2007, 45 (1): 77-92.

[13] 郝建华, 曾京, 邬平波. 铁道客车垂向随机减振及悬挂参数优化[J]. 铁道学报, 2006, 28(6): 35-40.

[14]ZhangYW,ZhaoY,ZhangYH,etal.Ridingcomfortoptimizationofrailwaytrainsbasedonpseudo-excitationmethodandsymplecticmethod[J].JournalofSoundandVibration, 2013, 332(21): 5 255-5 270.

[15]NishimuraK,PerkinsNC,ZhangWM.Suspensiondynamicsanddesignoptimizationofahighspeedrailwayvehicle[C]//Proceedingsofthe2004ASME/IEEEJointRailConference.Baltimore:IEEE, 2004: 129-139.

[16]翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015.

[17]InternationalOrganizationforStandardization.ISO2631-1MechanicalVibrationandShock-EvaluationofHumanExposuretoWhole-driverVibration-Part1:GeneralRequirements[S].Geneva:InternationalOrganizationforStandardization, 1997.

(编辑：郝秀清)

Optimization of secondary vertical suspension damping ratio for tram

YU Yue-wei, ZHOU Chang-cheng, ZHAO Lei-lei

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Fortheproblemofthedampingmatchingofsecondaryverticalsuspensionfortram,accordingtothe1/4vehiclebodythree-degree-of-freedomverticalvibrationmodeloftram,usingMATLAB/Simulink,anoptimaldesignsimulationmodelfordampingratioofsecondaryverticalsuspensionwasestablished.Takingoptimalridecomfortastarget,anoptimaldesignmathematicalmodelfordampingratioofsecondaryverticalsuspensionwasbuilt.Basedonthis,usingtrackverticalirregularityasinput,usingsuspensionverticalstrokeandtheverticaldynamicforceofprimarysuspensionasconstraintconditions,anoptimizationdesignmethodfordampingratioofsecondaryverticalsuspensionwaspresented.Withapracticalexampleoftram,thedampingratiowasdesigned.Theresultsshowthatthedampingratiovaluedesignedcansignificantlyimproveridecomfortoftram,thus,theoptimizationmethodofsecondaryverticalsuspensiondampingratiofortramiscorrect,whichwilllayagoodfoundationfortheoptimaldesignofsecondaryverticaldamper.

tram;secondaryverticalsuspensionsystem;dampingratiooptimization;three-degree-of-freedomverticalvibrationmodel

2015-11-09

国家自然科学基金项目(51575325)；山东省自然科学基金项目(ZR2013EEM007)；山东省重点研发计划项目(2015GGX105006)

于曰伟，男，yuyuewei2010@163.com；

周长城，男，greatwall@sdut.edu.cn

1672-6197(2016)06-0001-06

U482.1

A