一种碎边剪刀片的分析与加工①

刘潘儒

(常州宝菱重工机械有限公司， 江苏 常州　213019)



一种碎边剪刀片的分析与加工①

刘潘儒

(常州宝菱重工机械有限公司， 江苏 常州213019)

对一种碎边剪刀片的四刃口曲线进行了分析研究，将方程椭圆曲线简化成了圆弧，并结合刀片的使用工况，对简化形成的误差进行了计算分析，对比刀片的制作工艺，确定圆弧刀片的制作方法。

碎边剪； 刀片； 曲线方程； 曲率； 靠模

引　言

碎边剪是将圆盘剪或者双边剪剪下的废边进行分段剪切，以便收集运输到剪切机构[1]。目前薄板、中板剪切线上的碎边剪主要以滚筒式碎边剪为主，装于其上的刀片刃口也形式各异，但其刃口曲线基本都是圆柱面与平面斜交所形成的椭圆曲线[2]。由于当初设计思路的局限以及加工方法的制约，刀片只有一条刃口，使用中，若该唯一可用的刃口有较大的磨损或者崩口，那么这个刀片就必须报废。近年来，日本三菱日立公司设计了一种四刃口碎边剪刀片，提高了刀片的剪切量，在加工上也彻底否决了以往碎边剪刀片的制造方法。但是，这种四刃口碎边剪刀片的刃口曲线较复杂，其加工难度也随之加大，对刀片的加工工艺、工人的加工技术提出了更高的要求。

1　四刃口碎边剪刀片的简介

图1就是日本三菱日立公司设计的四刃口碎边剪刀片。它有四条完全相同的曲线刃口，刀片无需修磨，就可以使用四次。这种刀片一般用于剪切厚度1.5～6 mm，屈服强度小于320 MPa，抗拉强度小于440 MPa的碳钢薄板。刀片材料的硬度要求为HS 72～74，常规选材：6CrW2Si或5Cr5WMoSiV。

图1　四刃口碎边剪刀片

2　四刃口碎边剪刃口曲线的简化与误差分析

2.1四刃口碎边剪刀片刃口曲线

目前使用的四刃口碎边剪刀片的刃口曲线均是椭圆的一部分，它是圆柱被一平面斜交所形成的曲线的一部分，其中圆柱的方程为X2+(Y-R)2=R2，斜的平面的方程为X=Ztanα，如图2所示。

(1)

下刃口曲线与上刃口曲线关于X轴对称，故下刃口曲线在平面上的方程为

(2)

由于可以建立不同的坐标系，因此在形式上，上述方程会有所差异。

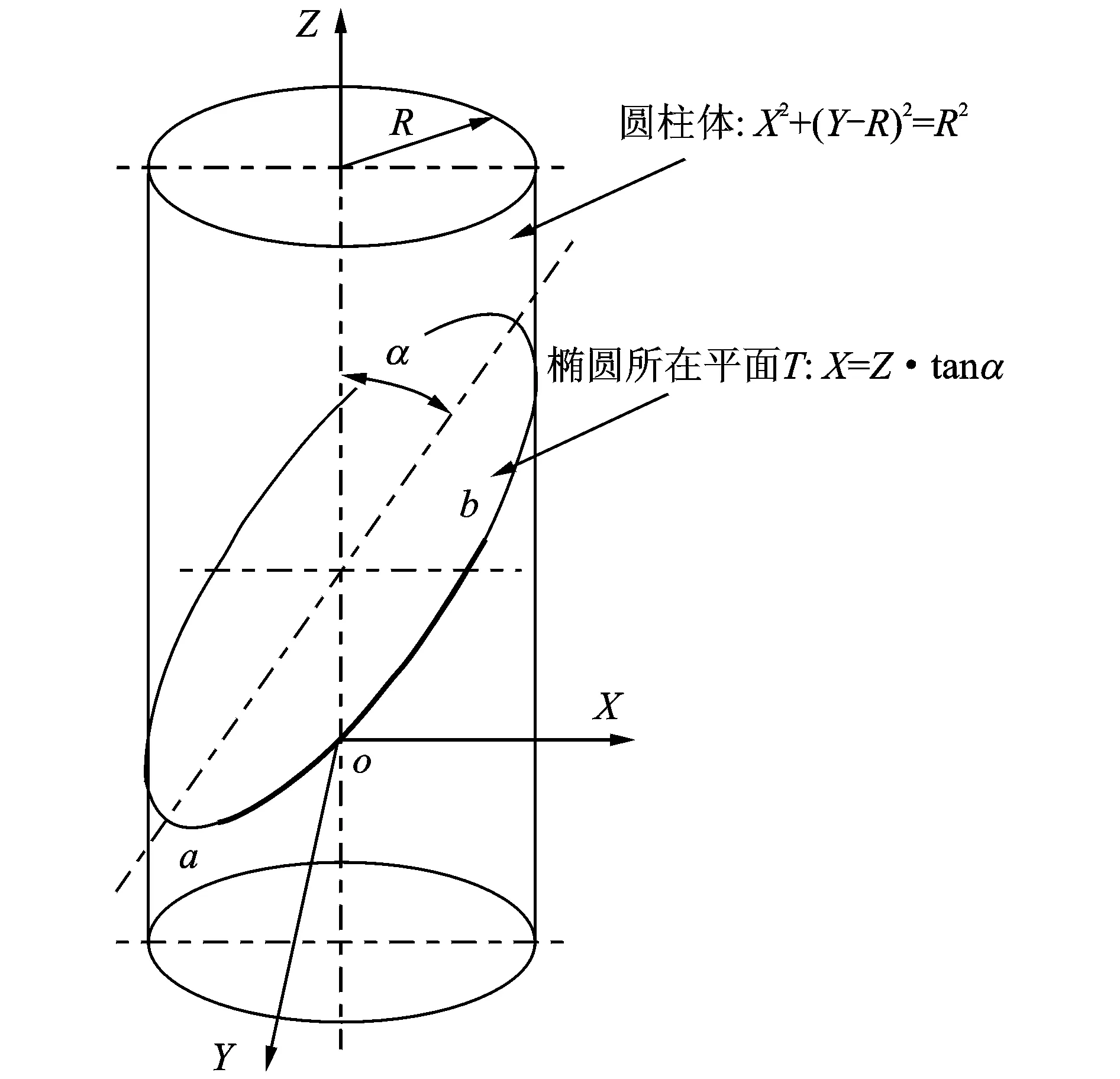
图2　圆柱及斜的平面的方程示意图

显然，在实际生产中，上面的方程无论计算或加工上都比较繁琐，其加工难度也较大。

2.2刃口曲线方程的简化及其误差计算和分析

这种替代后会产生多大的误差呢？从以上分析知，误差大小主要与圆柱体的半径R，刀片长度L和安装倾角α有关。显然，R越小，L越大，α越大，则误差越大。实际中，由于空间位置及剪切力等关系，一般限定L<300 mm，倾角最大为25°。

现以图1中刀片尺寸等为例，对误差进行分析：

参看圆弧与椭圆弧对比示意图3，在X=L/2=140 mm点时

Y1=Y1(140)=225-

由于废料导槽的导向作用，一般剪切均是在剪刃中部，且废料宽度也达不到263 mm(280×cos20°)，即有效宽度一般为100 mm，装配时，刀架的刀槽底面还有两片垫板(厚度t1=0.1 mm,t2=0.05 mm)可以调节，而且剪切时的上、下刀片剪切重叠量在0.2～0.5 mm之间选择，所以h=0.052 mm对剪切不会产生明显的影响。

由上，在99%的剪切情况下应该是在X=±L/2=±50 mm点内进行计算。现计算误差如下：

Y1=Y1(50)=0.651 mm，

Y2=Y2(50)=0.650 mm，

于是，可知在废料宽100 mm时，其最大误差h=0.001 mm。

所以，实际使用中，用圆弧R代替曲线完全不影响剪切。

图3　圆弧与椭圆弧对比示意图

3　四刃口碎边剪加工新工艺

目前滚筒式碎边剪，除极个别刃口是螺旋线外，其余刀片刃口都是椭圆曲线形状，以往刃口都是单面刃口，采用类似于滚筒刀架的工装来车削和淬火后的磨削刀片刃口就可以解决问题，但四刃口碎边剪刀片是双面四刃口形式，根本不能采用传统的外圆磨削。

目前，这种碎边剪常采用的加工工艺为：

1) 锻造毛坯并退火处理；

2)粗加工平侧面及两端面；

3)钻线切割预钻孔及钻攻两个螺孔；

4)检验；

5)淬火处理；

6)精磨两平面，光两侧面，精磨两端面；

7)线切割孔及刃口曲面至图样；

8)退磁，去毛刺，检验等。

本刀片主要难点就是第7道工序的刃口曲面的加工，以往常规加工方法有：

(1)线切割。取多个点，点越多，最后线切割出来的曲面越精确，比较麻烦，且取点精度和计算精度都有误差；

(2)仿形磨。是一种传统做法，需要靠模具，曲面的精度取决于靠模的精度；误差往往更大。现在一般不采用。

由上述误差分析可知，在一定条件下，实际应用中可以使用第三种方法：曲率简化法。简化成R刃口后，就消除了取点精度误差和计算误差，也无需靠模，理论上避免了以上两种常规加工方法的缺点。加工圆弧也相对简单，可以直接采用线切割的慢走丝。在设备许可的情况下，也可以采用数控磨。

4　结束语

刀片刃口曲线简化，既避免了取点模拟的较大误差，又节省了制造工装的费用，线切割R误差极小，简单易行，更适合批量生产，效率更高。

[1]许石民，孙登月．板带材生产工艺及设备[M]．北京：冶金工业出版社，2008.

[2]薛培.新型碎边剪力能参数的分析确定[J].冶金设备，1992,(5)：74—76.

[3]同济大学数学教研室.高等数学[M].北京：高等教育出版社,1996.

2015-08-04

TG333.2+1