非合作体附着下的组合体航天器自适应控制

陈雪芬，康国华2

（1.南京航空航天大学自动化学院，南京211106；2.南京航空航天大学航天学院，南京211106）

非合作体附着下的组合体航天器自适应控制

陈雪芬1，康国华2

（1.南京航空航天大学自动化学院，南京211106；2.南京航空航天大学航天学院，南京211106）

空间中非合作体附着航天器本体后，新组合体惯量参数未知、系统引入的动量变化未知，容易造成航天器姿态控制失稳。针对此问题，提出了一种基于非合作组合体整体惯量估计的自适应控制方案，实现不同情形附着下新组合体姿态的快速和高精度恢复。通过构造李雅普诺夫函数，对自适应控制方案稳定性进行了证明。搭建的某卫星被非合作组合体附着后的姿控仿真平台表明，在非合作体惯量参数未知、引入动量未知以及附着前系统状态不定等恶劣情况下，采用该算法的组合体姿控误差可收敛到一个极小的领域内，可以实现对非合作组合体系统快速而有效的控制。

非合作体附着；新组合体；自适应控制；惯量估计

0　引言

在实际空间应用以及空间对抗中，很多情况下涉及航天器附着的问题［1-2］。附着航天器既可能是合作目标，又可能是非合作目标。如果附着体是非合作目标［3］，则必须充分考虑对目标航天器姿控所带来的影响，这就需目标航天器具有快速恢复姿态控制的能力。

本文所研究的非合作体附着，是指外形尺寸未知、质量质心位置未知、运动形式未知的航天器附着（包括各种对接方式，机械抓取、黏附等）的情形。当带有一定质量和动量的物体附着在目标体上，必然造成组合体质量质心位置、惯量参数的改变，并带来姿态上的扰动。如何消除并预防附着体有意或者无意带来的姿态扰动是未来空间应用中非合作组合体姿态控制需要解决的新问题。

近年来，国内外对非合作组合体的姿态控制问题研究较少，但不少学者针对惯量矩阵未知或外干扰不定提出了一些控制策略。例如文献［4］研究了航天器在受到外部于扰和惯量参数不确定时的非线性鲁棒分散控制器的设计。文献［5］提出了一种自适应控制方案，用来解决刚体航天器惯量部分参数未知的问题，该控制器通过控制输入直接补偿航天器系统出现的惯量变化。文献［6］、文献［7］中则以反馈线性化为基础并采用神经网络设计补偿策略，应对航天器系统参数不确定性以及执行机构和外界干扰不确定的情况。非线性PID自抗扰控制技术［8-9］则利用特殊非线性特性来开发具有特殊功能的环节，并引入扩张观测器理论来对系统的总扰动进行估计补偿。另外，针对惯量矩阵未知的情形，不少学者也提出了通过卫星陀螺、加速度等传感器以主动识别的方式进行惯量等动力学参数在轨识别的研究［10-13］，基于在轨识别的基础，再进行进一步的控制方案研究。

本文主要以被非合作体附着的目标卫星姿控系统为研究对象，针对非合作体附着后造成新组合体惯量参数未知、引入动量未知的情况，基于惯量估计的思想，设计自适应控制方案来实现新组合体姿态的快速和高精度恢复或者响应。

1　问题与模型描述

1.1非合作附着

本文所研究的非合作体附着，是指外形尺寸未知、质量质心位置未知、运动形式未知的航天器附着情形。在图1所示的附着示意图中，带有众多未知参量的非合作体附着在目标航天器后，会给目标航天器带来明显扰动，造成新组合体系统的惯量、惯量参数未知，同时给系统引入未知冲量，带来新组合体姿态控制的困难。

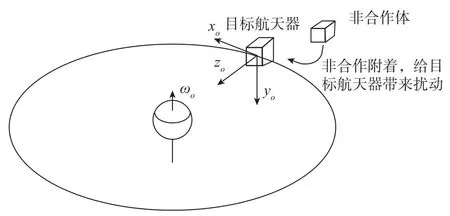
图1　非合作附着模型示意图Fig.1 Schematic diagram of non-cooperative attachment

1.2航天器姿态动力学

刚体航天器姿态动力学方程［14］为：

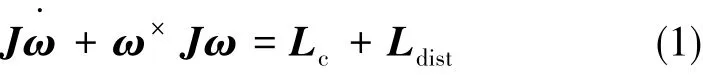
式中，ω∈R3为航天器本体坐标系相对于惯性坐标系的角速度矢量；Lc∈R3，Ldist∈R3分别表示航天器的控制力矩矢量和干扰力矩矢量；ω×为对于任意的ω=［ωxωyωz］T的斜对称矩阵。

因为本文的研究对象为非合作体附着后的新组合体的状态，故其惯量假设为三阶非对称矩阵。惯量矩阵表示如下：

1.3航天器姿态运动学

四元素qv描述的航天器姿态运动学方程［14-15］为：

由于目标四元素为常值，故可对上述误差四元素进一步求导得到：

2　自适应控制器设计

2.1控制器设计约束条件

1）干扰力矩矢量Ldist是有界的，满足‖Ldist‖≤Lmax，Lmax为未知的正常数。这一约束条件也是符合工程实践的；

2）航天器的惯量矩阵虽然为未知的，但是正定的常值矩阵；

3）非合作体附着的具体过程，本文不予考虑，仅考虑附着前后的状态；

4）非合作体附着后，新的组合体姿态机动的控制目标是使得被附着体可以在尽可能短时间内重新恢复到附着前的状态，并且控制力矩受限。

2.2自适应姿态控制

非合作体附着目标航天器之后，由于其自身带有惯量及一定大小的动量，会对原系统造成一定的干扰。当非合作体惯量过大，或者携带的动量过大，可能会导致原系统的控制方案失效，系统可能变为失控状态。

为了解决上述问题，令目标航天器控制力矩Lc满足如下自适应控制律：

其中，

1）x1，x2为系统三维状态变量，分别取为：

式中，ω为系统角速率，可以看作虚拟控制输入。

2）θ～为惯量估计，具体形式如下：

3）k2为非线性阻尼系数，k1＞0，k2＞0；

5）Y为根据动力学方程提取的惯量系数矩阵。

可以证明目标航天器在被非合作目标附着后，采用上述控制率依然可以保持稳定。

根据控制理论［16］，取李雅普诺夫函数：

式中，Δθ定义为航天器惯量参数的估计误差，即：

对V1求导得：

又x1=qe，ω=x2+αx1，故：

进而得到：

由式（8）可得：

将式（15）左右两边同左乘以J后可得：

令：

其中，航天器的惯量参数θ定义为：

惯量系数矩阵：

因为组合体惯量在非合作体附着后为未知的常值（非合作体在表面移动或者离开的情形除外），故可得：

所以，将式（16）、式（19）带入式（3）得：

将自适应控制律式（6）、式（7）代入式（20）得：

可见，当取k＞0且α＞0，则系统是全局渐近稳定的。即当t→∞时，x1→0，x2→0，从而进一步可得qe→0，ω→0。

3　仿真校验与评价

对某小卫星被非合作体附着后的新组合体姿态控制系统进行仿真，验证上述针对非合作体附着的自适应控制方案对不同附着情形下的控制效果。

3.1仿真参数设置

1）某被附着航天器原有惯量

2）仿真中，对非合作体的惯量量级设置了两个参数，分别为1∶1附着和1∶10附着情形。其中，J1为接近1∶1附着的非合作体惯量，J2为接近1∶10附着的非合作体惯量，由于非合作体惯量并不一定会呈现对称分布，故仿真选取的惯量阵如下：

3）航天器姿态参数初值设置

初始姿态为［81.9631 43.9854 -3.2675］°，对应的四元素初值为：

初始角速度：

4）控制参数选取

5）控制力矩受限，Lc≤0.1N·m。

3.2仿真结果

对某小卫星被非合作体附着后的新组合体姿态控制系统进行仿真研究。主要分为两个控制阶段，在第一阶段，目标星本体在自适应控制方案下的自身稳定控制；第二阶段为目标星被非合作体附着后导致系统失稳后的自适应控制，控制要求为使系统尽快恢复到稳定状态。具体的控制流程如图2所示。

图2　仿真控制流程图Fig.2 Flow chart of simulation control

非合作体本身具有一定动量，附着后，残余动量会给目标体带来冲击，导致系统角速度等发生变化。本文在仿真中，进行非合作体附着模拟，默认设置非合作体附着后引入动量，导致系统角速率瞬间变为：

（1）目标航天器维持原PD控制原卫星采用常用的基于姿态四元素的PD控制［17］，若被非合作附着后，不引入自适应控制，其在被1∶1非合作体附着，附着后控制效果如图3所示。

图3　仍维持原PD控制的非合作附着效果图Fig.3 Control effect of remaining PD control for the non-cooperative attachment

从图3可以看出，在1∶1附着条件下，维持原PD控制，虽然姿态最终也能恢复到稳定状态，但花费的时间大约需要320s，需要的控制时间较长。仅仅在最简单的附着情况下，效果就比本文设计的自适应控制方案差很多。同样的情况下，当引入很大冲量时，系统甚至完全失去控制（仿真曲线呈现发散状态）。

（2）接近1∶1的非合作体附着在新组合体惯量阵变化为 J1情况下，即在100s处被接近1∶1的非合作体附着，在自适应控制律下控制效果如图4所示。

图4　附着后惯量变为J1后的姿态控制效果Fig.4 Control effect of newinertia matrix J1

从图4看出，原卫星系统在约21s达到稳定状态；非合作体在100s处附着后，新组合体在大约156s处重新恢复到稳定状态，整个控制过程只用了56s。图3和图4两种控制方案的对比，揭示了相同附着条件下，本文自适应控制方案的效果要比原PD控制方案的效果好很多，并且可以实现非合作体附着后姿态的快速恢复，达到很好的控制效果。

（3）接近1∶10的非合作体附着

在新组合体惯量阵变化为J2情况下，在100s处被接近1∶10的非合作体附着，在本文设计的自适应控制律下控制效果如图5所示。

图5　附着后惯量变为J2后的姿态控制效果Fig.5 Control effect of newinertia matrix J2

从图5看出，即使附着体被10倍惯量大小的非合作体附着，新组合体在此自适应控制方案的控制下，仍然只需要400s左右就能稳定下来，姿态能够较快地收敛到一个较小的领域内，并渐渐趋于稳定。本文的控制系统对于不同惯量级的附着体都可以实现快速而有效地控制。

（4）附着体携带数10倍冲量

由于非合作体状态完全未知，非合作体可能携带很大冲量来蓄意破坏原卫星系统的状态。本仿真建立在原卫星本身完好，但需抵抗巨大冲击带来的扰动情况下。在新组合体惯量阵变化为J1情况下，即接近1∶1附着的情况下，在100s附着瞬间引入很大冲量，导致系统角速率瞬间产生数10倍的变化，控制效果如图6所示。

图6　附着瞬间引入数10倍角速率变化控制效果Fig.6 Control effect of cases when angle velocity changed dozens of times

附着体携带的冲量越大，瞬间引起新组合体的角速率变化越明显。从图4和图6的仿真曲线可以看出，当非合作体恶意附着目标卫星，即附着后引起很大角速率变化，新组合体系统的姿态在自适应控制方案的控制下，仍然可以较快地达到一个较小的领域内，并渐渐恢复到稳定状态。由仿真可得，本文的控制系统对于携带很大冲量的非合作体的附着均可以实现很好的控制。

（5）目标星姿态机动下的附着

在新组合体惯量阵变化为J2情况下，在10s附着。从曲线可以看出，在10s处原系统并未处于稳定状态，仍在机动过程中，在此时突然被非合作体附着，控制效果如图7所示。

从图5和图7的仿真曲线可以得到，即使非合作体以接近1∶10比例附着，无论原系统已经处于稳定还是在机动过程中，在本文提出的自适应控制方案的控制下，新组合体姿态一样可以较快地收敛到一个领域内，渐渐恢复到最终的稳定状态。由此可见，本文的控制系统对于原系统不同状态下的非合作附着均可以实现快速有效的控制。

（6）惯量估计结果

在新组合体惯量阵变化为J1和J2情况下，接近1∶1和1∶10附着，分别对应的惯量估计结果如图8（a）和图8（b）所示。其中，为了显示清楚，仅显示了主轴惯量的估计结果。

图7　附着瞬间处在机动过程中的控制效果Fig.7 Control effect of cases when attachment happens in the maneuver process

图8　非合作体附着后新组合体惯量估计结果Fig.8 Inertia estimation results of the new combination

从图8的仿真曲线可以发现，虽然控制律是基于惯量估计设计的，但是惯量估计的实际结果不是很理想，在1∶1附着时，可以实现一定程度上的估计，但精度不高；而当惯量相差较大时，则无法实现对惯量的准确估计。本文提出的姿态控制方案基于一定程度上的惯量估计。即使控制方案不能实现对惯量的准确估计，通过以上不同情况下的仿真表明，新组合体的姿态控制依然可以达到很好的效果。

4　仿真结果评价

上述各种情形下的仿真对比及其相关分析，可以揭示本文提出的自适应控制方案在各情形下的鲁棒性，即对非合作体惯量参数未知、引入动量未知以及附着前系统状态不定等情形都具有较好的鲁棒性。虽然控制惯量估计的实际结果不是很理想，不能实现对惯量的准确估计，但是姿态控制依然可以达到较好的效果，实现不同情形附着下新组合体姿态的快速和高精度恢复。

5　结论

本文主要研究了非合作体附着航天器本体后，由于新组合体惯量矩阵未知，引入动量未知等情况造成的航天器姿态控制问题。本文在航天器运动学和动力学的基础上，根据非合作附着干扰下组合体控制原则，设计了一种基于惯量估计的自适应控制方案，且通过构造李雅普诺夫函数给出了详细的证明。通过搭建非合作体附着仿真环境，对非合作体惯量参数未知、引入动量未知以及附着前系统状态不定等附着情形进行仿真，新组合体的姿态在本文提出的自适应控制方案控制下都能较快地收敛到一个较小的领域内，渐渐趋于稳定。本文提出的自适应控制方案对于非合作附着情形具有很好的控制效果，能够真正实现对姿态的快速精确控制。但是，本文提出的控制方案并不能在任何条件下都实现对惯量的准确估计。通过对非合作组合体姿控系统进行研究，对航天器在轨操作、空间攻防研究具有十分重要的指导意义。

［1］ 蔡远文，郭会，李岩.航天器在轨组装技术进展［J］.兵工自动化，2009，28（10）：6-14. CAI Yuan-wen，GUO Hui，LI Yan.Development of spacecraft on-orbit assembly technologies［J］.Ordnance Industry Automation，2009，28（10）：6-14.

［2］ 崔乃刚，王平，郭继峰，程兴.空间在轨服务技术发展综述［J］.宇航学报，2007，28（4）：805-811. CUI Nai-gang，WANG Ping，GUO Ji-feng，CHENG Xing.Development of on-orbit service technology［J］. Journal of Astronautics，2007，28（4）：805-811.

［3］ 李新刚，裴胜伟.国外航天器在轨捕获技术综述［J］.航天器工程，2013，22（1）：113-119. LI Xin-gang，PEI Sheng-wei.On-orbit capture technology of spacecraft［J］.Spacecraft Engineering，2013，22（1）：113-119.

［4］ Song B，Ma G，Li C.Robust fuzzy controller design for a rigid spacecraft attitude regulation system［C］.Proceeding of 1stInternational Symposium on Systems and Control in Aerospace and Astronautics，Harbin，2006：424-429.

［5］ Liang S，Wei H.Robust adaptive relative position tracking and attitude synchronization for spacecraft rendezvous［J］. Aerospace Science and Technology，2015，41（2）：28-35.

［6］ 袁国平.航天器姿态系统的自适应鲁棒控制［D］.哈尔滨工业大学，2013. YUAN Guo-ping.Adaptive robust control for spacecraft attitude system［D］.Harbin Institute of Technology，2013.

［7］ Thakur D，Srikant S，Akella M R.Adaptive attitude-tracking control of spacecraft with uncertain time-varying inertia parameters［J］.JournalofGuidanceControland Dynamics，2015，38（1）：41-52.

［8］ 韩京清.从 PID到自抗扰控制技术［J］.控制工程，2002，9（3）：13-18. HAN Jing-qing.FromPIDtotheactivedisturbance rejection control technique［J］.Control Engineering，2002，9（3）：13-18.

［9］ 于靖，陈谋，姜长生.基于干扰观测器的非线性不确定系统自适应滑模控制［J］.控制理论与应用，2014，31 （8）：993-999. YU Jing，CHEN Mou，JIANG Chang-sheng.Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer，2014，31（8）：993-999.

［10］ Wilson E，Lages C，Mah R.On-line gyro-based，massproperty identification for thruster-controlled spacecraft using recursive least squares［C］.Proceedings of the 45th

IEEE International Midwest Symposium on Circuits and Systems，Tulsa，Oklahoma，2002.

［11］ Jo S C，BangH.Masspropertyestimationofgyroless spacecraft［C］.11thInternational Conference on Control，Automation and Systems，Korea，Kintex，Gyeonggido，2011.

［12］ Slotine E，Li W.Composite adaptive control of robot manipulator［J］.Automatica，1989，25（4）：509-519.

［13］ 刘伟霞，熊智，刘建业.组合航天器转动惯量在轨两步辨识标定［J］.中国空间科学技术，2013，33（2）：32-40. LIU Wei-xia，XIONG Zhi，LIU Jian-ye.Two-step identification of inertia of combination of spacecrafts on orbit［J］.Chinese Space Science and Technology，2013，33（2）：32-40.

［14］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998. ZHANG Ren-wei.Satellite orbit attitude dynamics and control［M］.Beijing：Beihang University Press，1998.

［15］ 宋斌，李传江，马广富.航天器姿态机动的鲁棒自适应控制器设计［J］.宇航学报，2008，29（1）：121-125. SONG Bin，LI Chuan-jiang，MA Guang-fu.Spacecraft attitude maneuver adaptive robust controller design［J］. Journal of Astronautics，2008，29（1）：121-125.

［16］ 陈复扬，姜斌.自动控制原理［M］.北京：国防工业出版社，2010. CHEN Fu-yang，JIANG Bin.Principles of automatic control［M］.Beijing：National Defense Industry Press，2010. ［17］ Liu Y Z，Ma X M.Quaternion based adaptive control of a spacecraft with reaction wheels［J］.Journal of Shanghai Jiaotong University，2013，37（12）：1957-1961.

Adaptive Control Scheme for the New Spacecraft Combination after Non-cooperative Attachment

CHEN Xue-fen1，KANG Guo-hua2
（1.School of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106；2.School of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 211106）

While non-cooperative attachment happens in space，the inertia of the new combination would be unknown，as well as the change of system momentum.This may lead to the instability of spacecraft attitude control.In order to solve the problem，this paper proposes an adaptive control scheme based on estimation of the new combination.And it can make the new combination of different situations reach the stable state with high precision and fast speed.In this paper，the stability of the adaptive control scheme is proved by constructing a Lyapunov function.The simulation environment of a satellite with non-cooperative attachment is constructed.It shows that the attitude error would converge to a small field by using the control scheme regardless of the awful cases，including unknown inertia parameters，added momentum and system status before the attachment.Besides，the simulation results show that the new combination system can be effectively and quickly controlled by the control scheme.

non-cooperative body attachment；new combination；adaptive control scheme；inertia estimation

V448.22+3

A

1674-5558（2016）01-01206

10.3969/j.issn.1674-5558.2016.04.003

2015-10-15

江苏省自然科学基金项目（编号：SBK201343261）

陈雪芬，女，导航、制导与控制专业，硕士，研究方向为多传感器数据融合、卫星姿态控制。