基于L1自适应控制律的无人机滚转控制
张 磊,杨凤田,周文雅,黄 俊
(1.沈阳飞机设计研究所,沈阳 110135;2.沈阳航空航天大学辽宁省通用航空重点实验室,沈阳 110136;3.辽宁通用航空研究院,沈阳 110136;4.大连理工大学航空航天学院,大连 116024;5.北京航空航天大学航空科学与工程学院,北京 100083)
随着航空器在无人控制方面的发展,各种控制算法被广泛研究,包括PID (proportional integral derivative)控制[1]、线性二次型控制(linear quadratic regulator,LQR)、模糊控制[2]、遗传算法控制、神经网络控制、反馈线性化控制、模型预测控制[3]、反步控制[4]和自适应控制等。其中设计PID控制算法时,需要先将无人机复杂的非线性动力学模型在某些特定状态下(如定常水平直线飞行或定常盘旋飞行)简化为线性模型,再将纵向和横侧向解耦,并分别设计PID控制律来控制升降舵、油门、副翼和方向舵等操纵机构。尽管PID控制器在设计过程中考虑了裕度范围,但仍然对数学模型的精确程度存在较强的依赖。其PID控制参数无法根据无人机实际飞行状态进行调整[5]。模糊控制、遗传算法控制和神经网络控制等智能控制方法虽然具有较少依赖控制模型精确参数的优点,但其控制系统很难用精确的数学原理去描述,很难用系统分析方法去优化控制器。而自适应控制方法对系统内部模型参数和外部干扰信息依赖较少,可以在系统运行过程中逐步改善控制,具有一定的适应能力。自适应控制包括模型参考自适应控制(model reference adaptive control,MRAC)和自校正控制等。其中模型参考自适应控制针对存在不确定性的系统参数和结构,具有自适应调节控制器增益权重的优点,但其控制稳定性受参数和外部干扰因素不连续性的影响较大。自适应滑模控制具有较强的鲁棒性和较快的响应速度,但存在易抖振缺点[6]。因此,在自适应控制方法基础上加以改进的控制算法越来越多地被引入无人机控制与制导中[7-9]。
L1自适应控制律,是在模型参考自适应控制算法基础上,引入低通滤波器将高频振荡信号过滤,进而减轻控制律的振荡,使其既具有良好的适应性,又具有良好的鲁棒性[10-12]。王俊玲等[13]采用基于线性二次型调节器的L1自适应控制方法进行了无人机横侧向控制,仿真结果表明所设计的控制器可以实现对跟踪误差的快速收敛。薛静等[14]采用L1自适应控制方法进行无人机横侧向控制,仿真结果表明所设计的控制器可以适应飞机不确定因素和外部干扰,具有良好的瞬态性能和鲁棒性。胡龙珍等[15]采用L1自适应控制方法对无人机进行俯仰控制,针对无人机模型不确定性、舵面效能变化等情况进行仿真分析,得出所设计的控制器具有良好的鲁棒性能。
针对存在参数不确定性的无人机滚转通道模型,分别设计了L1自适应控制律和PD控制律,实现了滚转通道控制,并对比分析了这两种控制算法的效果和关键因素。
1 无人机动力学模型
无人机动力学方程为非线性方程组,为了简化控制对象,采用小扰动原理将其化简为配平状态下的线性方程组,配平条件可为定常水平直线飞行或定常盘旋飞行等。线性化时可假设无人机油门固定不变,没有风干扰,则无人机横侧向运动方程可化为小扰动方程,即
(1)
(2)
(3)
(4)
式中:β为侧滑角;p为滚转角速度;r为偏航角速度;φ为滚转角;δa为副翼偏角;δr为方向舵偏角;μe为航迹倾斜角;θe为俯仰角,g为重力加速度;V为速度;A为系统状态矩阵;B为控制矩阵;E为雅克比矩阵[16];气流坐标轴系内力和力矩的量纲导数定义如下:
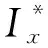
若采用副翼控制滚转角,方向舵不参与滚转角控制,方向舵保持中立位置,则可以将式(1)化为
(5)
(6)

2 L1自适应控制理论
L1自适应控制方法以模型参考自适应控制算法为基础,在控制输入端添加一个低通滤波器来滤除高频干扰信号。其既具有根据控制对象参数变化而自动调整控制律的优点,又具有抗高频干扰的优点,是一种快速鲁棒的控制方法[17]。L1自适应系统包括四个部分:被控对象、状态观测器、自适应律和控制律[18]。
重点考虑包含时变未知参数向量的被控对象的L1自适应控制设计。
被控对象采用状态空间形式描述,即
(7)
式(7)中:x(t)为可观测的系统状态向量;u(t)为控制向量;θ(t)为时变未知参数向量;y(t)为输出向量;c为系统输出矩阵,其中:
u(t)=u1(t)+u2(t)
(8)
u2(t)=-hTx(t)
(9)
则式(7)可以简化为
(10)
设计向量h,使Am为Hurwitz矩阵,其表达式为
Am=A-bhT
(11)
设计状态观测器为
(12)
根据状态观测器测得的估计值和实际值之间的误差值,设计自适应律为
(13)
式(13)中:Γ为系统的自适应增益。

(14)
P为正定对称矩阵,并且满足
(15)
Proj(*,*)为投影算子,且有
Q=QT>0
(16)
设计控制向量u1(t)为
(17)
式(17)中:C(s)为低通滤波器;r(t)为参考输入向量,且有
(18)
H(s)=(sI-Am)-1b
(19)
则可以推导得到
(20)
式中:I为单位矩阵。
低通滤波器C(s)设计时,需要满足如下条件:
(1)C(s)渐进稳定,严格正则,且低通增益C(0)=1。
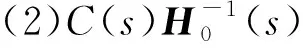

L1自适应控制系统结构图如图1所示。
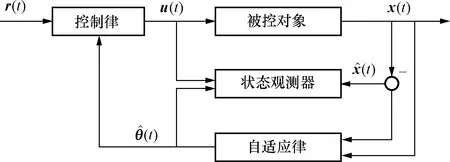
图1 L1自适应控制系统结构图Fig.1 System diagram of L1 adaptive control law
3 仿真分析
研究对象为某型固定翼无人机,分别利用PID控制律和L1自适应控制律实现了无人机的滚转角控制。重点给出L1自适应控制律的设计过程。在无人机定常水平直线飞行时,无人机横侧向动力学方程[19]为

(21)

(22)
求解矩阵A的特征根为-15.295 9、-2.060 4±5.906 2i、-0.022 1,可知系统虽然是稳定的,但稳定裕度不理想,因此采用极点配置法进行调节,令hT=[-0.019 5 -1.640 5 -0.040 8 -5.157 5]。
假设系统模型的时变未知参数向量的变化范围为
|θi(t)|≤0.7,i=1,2,3,4
(23)

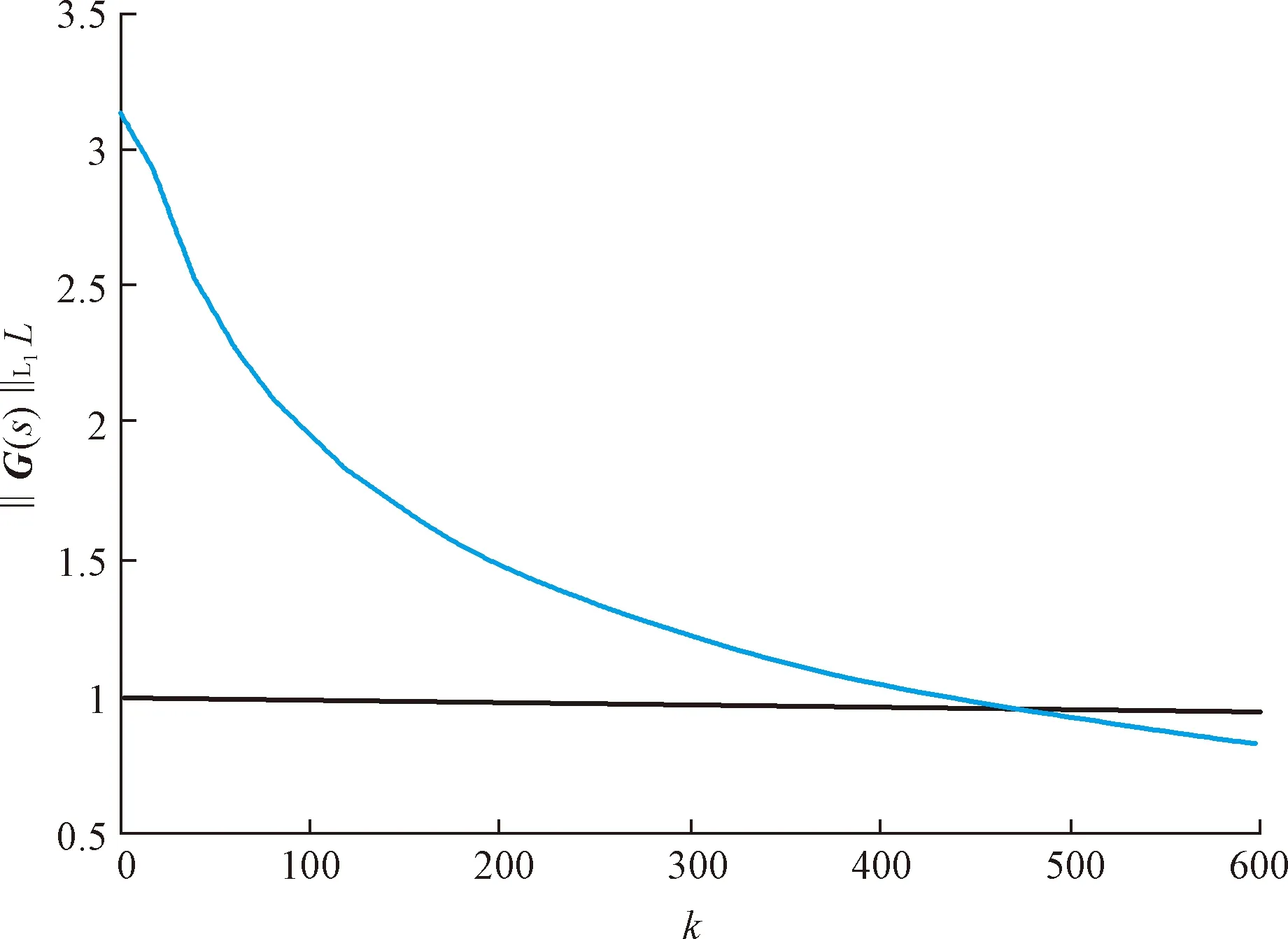
图随k的变化曲线Fig.2 The simulation curve of with k
根据图2可以选定k=600,则低通滤波器为
(24)
假设无人机滚转角有1°的初始值,则分别采用L1自适应控制方法和PD控制律将滚转角调整为0°。对理想模型θT=[0 0 0 0]和变参模型θT=[0 -0.7 0 0]分别进行L1自适应控制仿真和PD控制仿真,结果如图3所示。

图3 理想模型θT=[0 0 0 0]和变参模型θT=[0 -0.7 0 0]仿真结果Fig.3 The simulation results of ideal model θT=[0 0 0 0] and variable parameter model θT=[0 -0.7 0 0]
由图3可知,仿真中所设定的时变未知参数向量θ(t)对L1自适应控制效果几乎没有影响,即L1自适应控制能够很好地克服参数不确定性的影响;然而,对时变未知参数向量θT=[0 -0.7 0 0]存在时,PD控制律无法对该变参模型进行良好控制,滚转角呈现振荡发散状态,无法回到指令要求的0°。
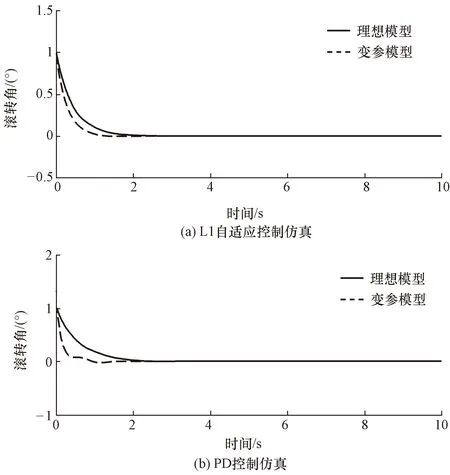
图4 理想模型θT=[0 0 0 0]和变参模型θT=[0.7 -0.3 0.7 0.7]仿真结果Fig.4 The simulation results of ideal model θT=[0 0 0 0] and variable parameter model θT=[0.7 -0.3 0.7 0.7]
由图4可知,仿真中所设定的时变未知参数向量θ(t)对L1自适应控制效果和PD控制效果都几乎没有影响,即L1自适应控制和PD控制律均能够很好地克服这种条件下的参数不确定性的影响,其中L1控制效果比PD控制效果略好。
与上述过程相似,当θT=[-0.7 -0.7 -0.7-0.7]时,分别对理想模型和该变参模型进行L1自适应控制仿真和PD控制仿真,结果如图5所示。
由图5可知,仿真中所设定的时变未知参数向量θ(t)对L1自适应控制效果几乎没有影响。时变未知参数向量θT=[-0.7 -0.7 -0.7 -0.7]存在时,PD控制的滚转角呈现振荡变化状态,收敛很慢,无法对该变参模型进行有效的滚转角控制。
按照上文仿真方法,分别对θ(t)进行赋值仿真,得到L1自适应控制效果和PD控制效果对比见表1。
由表1可知,不论θ(t)如何变化,L1自适应控制律始终能保持良好的滚转角控制,而PD控制律则只能在一定θ(t)取值范围内保持良好控制能力。在PD控制系统中,θ2对PD控制系统影响较大。
由式(10)可以推得
(25)
时变参数不确定性θ(t)通过与控制矩阵b相

表1 θ(t)分别赋值L1自适应控制和PD控制效果Table 1 L1 adaptive control law and PD control law with θ(t) assign values separately
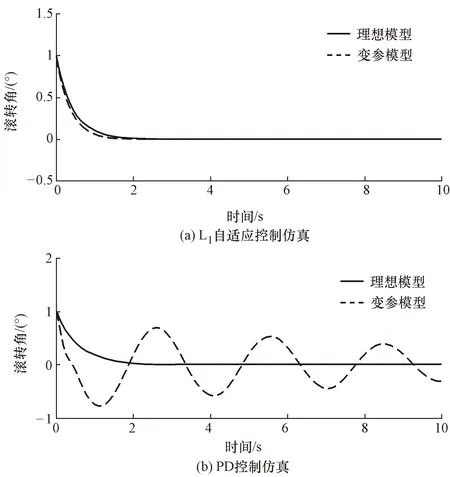
图5 理想模型θT=[0 0 0 0]和变参模型θT=[-0.7 -0.7 -0.7 -0.7]仿真结果Fig.5 The simulation results of ideal model θT=[0 0 0 0]and variable parameter model θT=[-0.7 -0.7 -0.7 -0.7]
乘,分别对侧滑角,滚转角速度,偏航角速度,滚转角的控制效果产生影响。由式(22)可知,本算例无人机的控制矩阵b中各元素取值分别为b1=0,b2=-175.593 9,b3=15.683 5,b4=0,其中b2绝对值较大,根据表1中PD控制效果和式(25),可以判断,本算例无人机的参数不确定性θ2主要通过b2θ2这个系数影响控制系统。根据式(5)可知,b2θ2对滚转角速度产生影响,滚转角速度变化后又对滚转角产生影响,由于PD控制律无法根据θ2的变化而相应做出控制增益调整,导致PD控制系统受到θ2较大影响。而对于L1自适应控制系统,虽然时变参数不确定性θ(t)也对该系统产生了相同作用,但L1自适应控制律可以根据θ(t)的变化自动进行相应的调节,只要θ(t)在本文定义集合范围内发生变化,其滚转角控制效果始终良好。
4 结论
以某型无人机横侧向控制为例,在考虑时变未知参数向量θ(t)条件下,分别设计L1自适应控制律和PD控制律,根据θ(t)变化范围选取具有代表性的典型值,开展两种控制律作用下的MATLAB仿真,得到以下结论。
(1)当时变未知参数向量在±0.7范围内取值时,L1自适应控制律能够克服参数不确定对控制系统的影响,始终具有良好的滚转角控制效果。
(2)PD控制只能适用于一定范围内的模型参数变化,尤其对参数θ2的变化较为敏感,这是因为PD系统无法根据由于存在不确定参数θ2导致的滚转角控制回路的变化而做出控制增益调整。
(3)从仿真结果可以看出,对于某型无人机滚转角控制,L1自适应控制律比PID控制更为有效,鲁棒性强,这对无人机飞行控制系统设计具有重要的参考价值。

