基于载体姿态测量的微伺服吊舱

宋 夏，丁祝顺，丁 伟，蒋鸿翔，张 巍

（北京航天控制仪器研究所，北京100039）

基于载体姿态测量的微伺服吊舱

宋 夏，丁祝顺，丁 伟，蒋鸿翔，张 巍

（北京航天控制仪器研究所，北京100039）

针对微小型无人机光电吊舱对光轴稳定与目标跟踪的需求，研究了一种基于载体姿态测量的光学平台稳定技术。该技术利用吊舱基座上的速率陀螺测量机体三轴姿态运动，通过控制光学平台的俯仰和偏航两通道伺服系统实现对光轴的惯性空间稳定。该系统使用步进电机来当执行机构，根据步进电机的特性，可以推导得到控制量与转速的关系，由此省去了在一般捷联稳定技术中的微分测速环节，得出了一种新的基于前馈控制的不变性原理。设计了解耦指令分配算法，将一个两轴耦合系统，转换为两个独立的单轴系统。在单轴控制中，分别设计了比例控制及比例积分控制算法实现对光轴的稳定控制和跟踪。最后通过在 Matlab/Simulink环境下的仿真，以及实际的摇摆台试验，证明了基于载体姿态测量的稳定技术能够实现微小型无人机光电吊舱的光轴稳定。

光轴稳定；步进电机；基于姿态测量的稳定技术

0　引言

相比于大型无人机，微小型无人机在飞行中更容易受到风的影响而造成姿态大幅变化，从而造成光电吊舱的光学载荷视轴不稳定，影响光学载荷的清晰成像。为了克服这些影响，必须通过陀螺稳定平台将光学载荷的视轴与载体的运动和振动相隔离，保持视轴的稳定。考虑到由于微小型无人机光电吊舱的体积非常有限，精度较高的陀螺无法放入载荷舱与光学载荷固连，因此可采用基于姿态测量的稳定控制，将陀螺与吊舱基座固连，通过解算实现视轴稳定。本系统的执行机构采用了步进电机驱动方式，通过记录步进电机的转动步数来记录框架角位置，并可以直接得到输入控制量与输出转速间的关系，与一般的捷联稳定方案相比，省去了微分测速环节，采用直接的前馈方式来实现视轴的稳定。

1　平台结构及坐标系定义

两轴平台伺服系统如图1所示［3］，由内到外依次为:载荷组件（可见光相机），俯仰框架，方位框架。陀螺安装在基座上，两个框架轴两端分别安装电机。

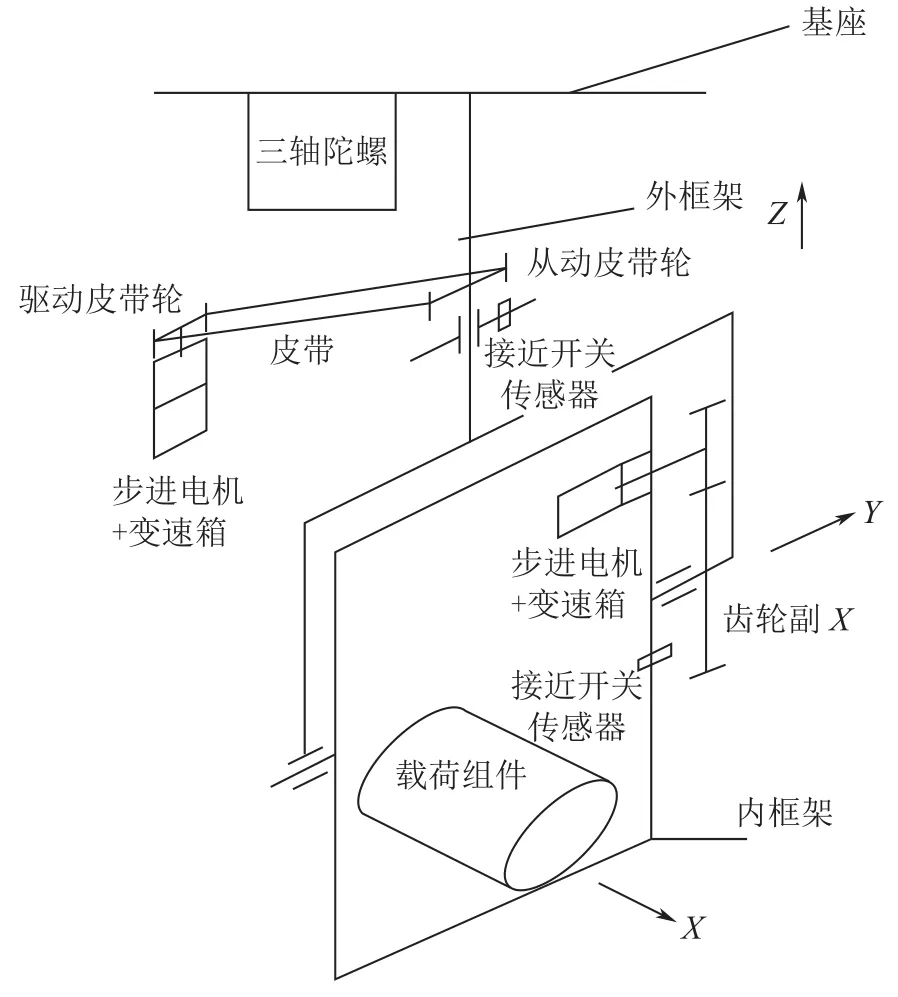
图1　两轴稳定平台结构Fig.1 The structure of two-axis platform

惯性平台各个坐标系的关系如图2所示。其中，O-XbYbZb为机体坐标系；O-XaYaZa为方位框坐标系，其为机体坐标系绕Zb轴旋转λa角度后得到；O-XfYfZf为俯仰框坐标系，其为方位框坐标系绕Ya轴旋转λf角度后得到，摄像机安装在俯仰框架上，光轴与Xf平行。为机体坐标系到方位坐标系的旋转变换，为方位坐标系到俯仰坐标系的旋转变换［1］。

图2　坐标系定义Fig.2 The definition of coordinate system

2　基于姿态测量光电稳定平台运动学建模

根据两轴双框架基于姿态测量光电稳定平台的结构形式与复合轴系系统的运动原理，俯仰框的运动是俯仰框自身转动和偏航框耦合运动的合成，偏航框的运动是偏航框自身转动和机体运动共同引起的。因此，基于姿态测量光电稳定平台视轴的运动是由机体、偏航框和俯仰框的运动合成得到的，其运动学方程需通过各轴系坐标系之间的旋转变换进行分析。

根据框架结构和复合运动原理，内框的运动由内框自身运动与外框耦合运动合成，外框运动由外框自身运动和机体运动合成，光轴的运动由内框、外框及机体运动所合成。

令基座在惯性坐标系中的三轴角速度为:ωb（t）=［ωbxωbyωbz］T，外框三轴角速度为:ωa（t）= ［ωaxωayωaz］T，内框三轴角速度为:ωf（t）= ［ωfxωfyωfz］T。

方位坐标系相对于惯性坐标系的角速度矢量为:

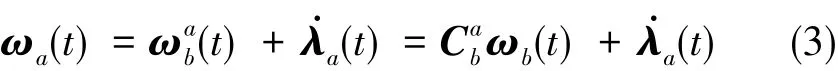
将式（1）带入式（4），则方位框角速度分量为:

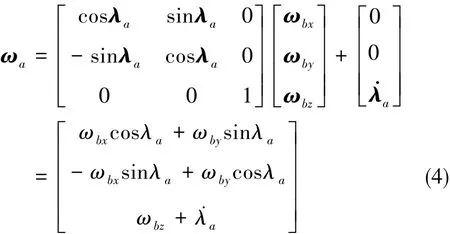
同理，ωa（t）将通过Oyf轴的几何约束和摩擦约束耦合到俯仰框坐标系中，令此耦合速度矢量为:

则俯仰框坐标系相对于方位框坐标系的角速度矢量为:

将式（2）、式（4）带入式（7）得俯仰框角速度分量为:

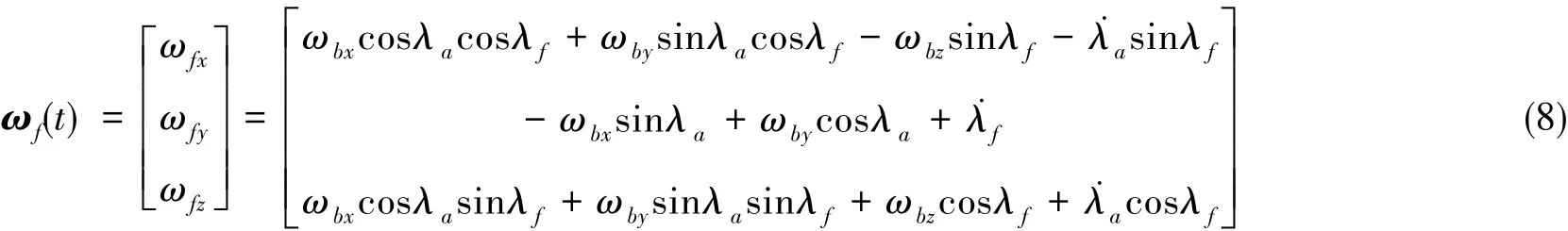
光电稳定平台的主要任务是隔离基座扰动，保证光轴在惯性空间中的稳定，根据运动学分析可以得到光轴稳定方程，即:

根据式（9）可以分别得到方位与俯仰轴的输入控制量，即 ˙λa与 ˙λf的表达式。

3　光学平台稳定控制

3.1速率环稳定

两轴微吊舱单轴基于姿态测量稳定原理概括如下（以俯仰轴为例）:假设机体在惯性空间中具有角运动，由于摩擦力矩、质量偏心等干扰因素的影响，引起框架（吊舱）在惯性空间的角运动。与利用陀螺直接测量框架的惯性空间角速率不同，基于姿态测量方式是利用机体上陀螺测得机体三轴姿态变化，伺服系统通过将三轴姿态变化解算为两框架上的控制信号，得到的值作为速率稳定控制路的输入量，由速率稳定控制环节计算得到电机控制量，驱动电机和框架运动，从而抵消机体运动带来的视轴晃动。控制框图如图3所示。

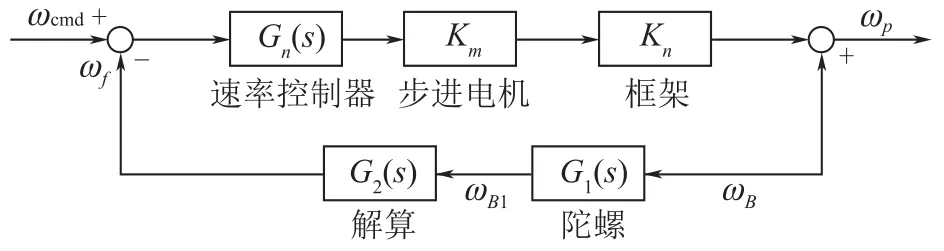
图3　控制原理框图Fig.3 The frame of control

在图3中，ωcmd为跟踪指令，ωp为平台惯性空间角速度，ωB为机体姿态扰动角速度，ωf为角速度反馈信息，G1（s）为陀螺传递函数，G2（s）为解算环节传递函数，Gn（s）为速率控制器，Kn为框架运动学传递函数，Km为步进电机传递函数。

由图3可以得到ωp的表达式为:

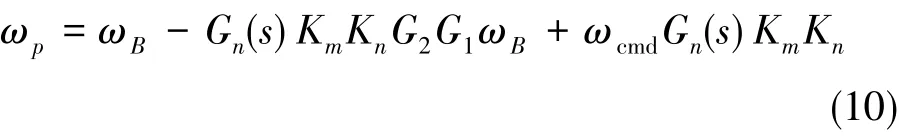
为了便于分析基座的耦合作用，令式（10）中的跟踪指令ωcmd=0，由式（10）得到基座扰动输入ωB单独作用下的平台输出角速度为:

在式（11）中，ω′p是只有基座扰动ωB作用下平台的角速度，要消除基座运动对视轴指向的耦合作用（即ω′p=0），代入式（12）中，得出理想情况下基于姿态测量稳定完全解耦的条件，也即系统对基座扰动的完全不变性原理为:

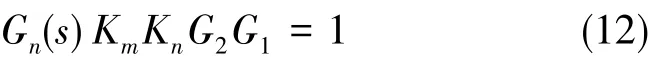
由式（12）可知，在基于姿态测量稳定中，基座扰动是影响姿态测量稳定的主要因素。

若要保证视轴的稳定，则需要Gn（s）KmKnG2G1=1。其中，G1（s）=1000，Km=0.005，角度为0°时，解算系数G2=1，由于本系统使用的是步进电机。因此，速率控制器发出控制指令时，电机每接收到1个脉冲信号，就相应转动一步，框架也随其一同转动特定角度，这里框架模型可以近似为Kn=1，将以上数据带入式（12）可得Gn（s）=0.2。

文献［11］介绍了一般的捷联稳定方案，其控制原理如图4所示。

其推导出基座扰动输入ωB单独作用下平台的角速度为:

图4　一般的捷联稳定方案控制原理Fig.4 Control principle of usual strapdown stabilization technique

在式（13）中，ω′p是只有基座扰动ωB作用下平台的角速度，要消除基座运动对视轴指向的耦合作用（即使ω′p=0），代入式（13），得出理想情况下一般的捷联稳定完全解耦的条件，即系统对基座扰动的完全不变性原理为:

可以看出，在本系统中，由于空间结构十分有限，设计中没有加入角位置或角速度传感器，而是使用步进电机经过计算其转动的步数来测量角度，并根据步进电机的特性推导得到框架的角速度，因此得到的完全不变性原理与文献中有所不同。

3.2位置环稳定

微小型吊舱位置环控制框图如图5所示，其中跟踪控制器Gp（s）采用PI控制。

图5　位置环控制框图Fig.5 The control frame of position loop

当系统输入为单位阶跃响应时，系统的输出如图6所示。

从图6中可以看出，对于PI控制而言，系统超调量为18%，上升时间为0.171s，系统输出响应速度较快，具有良好的动态和稳态性能。

当目标以幅值为1°，频率为1Hz的正弦信号运动时，系统输入及输出曲线如图7所示。

由图7可以看到，当目标以幅值为1°，频率为1Hz的正弦信号运动时，输出曲线能够实现有效跟踪，仅仅在相位上有一些滞后。

图6　系统阶跃信号输出Fig.6 System output of step response

图7　系统输入输出曲线Fig.7 System input and output

4　实验分析

选用某台基于姿态测量稳定的微小型吊舱，将它固定在两轴摇摆台上，使视轴跟踪某一目标，让摇摆台分别按1°/1Hz、3°/0.4Hz、5°/0.2Hz摆动，所测得的跟踪精度如表1所示，图8和图9是输入为1°/1Hz时方位轴与俯仰轴跟踪误差。

表1　不同扰动下所测得的系统跟踪精度Table 1 System tracking accuracy in different distribution

图8　方位轴跟踪响应曲线Fig.8 The tracking output of azimuth axis

图9　俯仰轴跟踪响应曲线Fig.9 The tracking output of pitch axis

5　结论

本文对基于姿态测量稳定技术在两轴微小型吊舱中的应用进行了详细的研究，制定出了基于姿态测量式光电稳定平台伺服控制方案，针对某基于姿态测量式稳定微小型吊舱做了摇摆台实验，

得到了俯仰轴与方位轴的跟踪精度，数据表明采用基于姿态测量式稳定方式能够达到微小型吊舱视轴稳定的功能，同时还大大节省了吊舱内部空间，更有助于吊舱内部的散热，因此基于姿态测量稳定技术对于微小型吊舱来说，不失为一种有效的稳定方式。

［1］ 陆元九.惯性器件（上册）［M］.北京：中国宇航出版社，1993. LU Yuan-jiu.Initial devices（Vol.1）［M］.Beijing：China Aerospace Press，1993.

［2］ 陆元九.惯性器件（下册）［M］.北京：中国宇航出版社，1993. LU Yuan-jiu.Initial devices（Vol.2）［M］.Beijing：China Aerospace Press，1993.

［3］ 王连明.机载光电平台的稳定与跟踪伺服控制技术研究［D］.中国科学院长春光学精密机械与物理研究所，2002. WANG Lian-ming.Study of stability control technology of airborne photoelectric platform and tracking servo［D］. Changchun Optical Precision Machinery and Physics Research Institute of Chinese，2002.

［4］ 傅建纲.惯性平台稳定回路的设计研究［D］.哈尔滨工程大学，2005. FU Jian-gang.Design and research of inertial platform stabilization loop［D］.Harbin Engineering University，2005.

［5］ 贾琳，孟伟锋.惯性平台稳定回路的双闭环控制［J］.科学技术与工程，2009，9（5）：1147-1149. JIA Lin，MENG Wei-feng.Double loop of inertial platform stabilization loop control［J］.Science Technology and Engineering，2009，9（5）：1147-1149.

［6］ 毕永利，刘洵，葛文奇.机载多框架陀螺稳定平台速度稳定环设计［J］.光电工程，2004，31（2）：16-18. BI Yong-li，LIU Xun，GE Wen-qi.Airborne multi frame

［7］ gyroscope stabilized platform velocity stabilized loop design ［J］.Opto Electronic Engineering，2004，31（2）：16-18.

［7］ 黎志强，许兆林，徐景硕.机载光电跟踪平台的控制系统设计［J］.电光与控制，2009，16（11）：60-63. LI Zhi-qiang，XU Zhao-lin，XU Jing-shuo.Design of system of airborne electro-optical tracking system［J］. Electro Optic and Control，2009，16（11）：60-63.

［8］ 周瑞青，刘新华，史守峽，王开斌.捷联导引头稳定与跟踪技术［M］.北京：国防工业出版社，2010. ZHOU Rui-qing，LIU Xin-hua，SHI Shou-xia，WANG Kaibin.Strapdown seeker stabilization and tracking of missile technology［M］.Beijing：National Defense Industry Press，2010.

The Micro Servo Pod Based on the Carrier's Attitude Measurement

SONG Xia，DING Zhu-shun，DING Wei，JIANG Hong-xiang，ZHANG Wei
（Beijing Institute of Aerospace Control Devices，Beijing 100039）

A pitch/yaw semi-strapdown optical platform stabilization technology based on stepper motor has been proposed to meet the demand of optical axis stability and target tracking on micro UAV pod.The tri-axial attitude motion of aircraft can be measured by the inertial device on the foundation bed of pod.The optical axis inertial space stability can be achieved by controlling the optical platform pitch and yaw servo system.The system uses stepper motor as actuator.According to the features of stepper motor，this essay deducts the relationship between the rolling rate and controlling variable. Therefore，cutting out the differential speed link in the usual strapdown stabilization technique，we can draw a new theory about immutability based on feedforward control.The design of decoupled instruction allocation makes a two-axis coupling system into two independent single axis systems.In the single axis control，the essay design proportional control and proportional integral control algorithm respectively to achieve the control and tracking stability of optical axis.Finally，the simulation in Matlab/Simulink and the experiment of vacillation demonstrate the stabilization technique based on attitude measurement can achieve the optical axis stability of micro UAV pod.

optical axis stabilization；stepper motor；stabilization technique based on attitude measurement

U666.1

A

1674-5558（2016）01-01071

10.3969/j.issn.1674-5558.2016.03.007

2015-02-06

宋夏，男，硕士，研究方向为导航、制导与控制。