基于损伤力学的GH4169合金低循环裂纹萌生寿命预测

初金阳，胡殿印，2，毛建兴，王荣桥，2，申秀丽，2

（1.北京航空航天大学能源与动力工程学院；2.先进航空发动机协同创新中心：北京100191）

基于损伤力学的GH4169合金低循环裂纹萌生寿命预测

初金阳1，胡殿印1，2，毛建兴1，王荣桥1，2，申秀丽1，2

（1.北京航空航天大学能源与动力工程学院；2.先进航空发动机协同创新中心：北京100191）

为了更准确地预估高温材料的低循环疲劳裂纹萌生寿命，将低循环疲劳的裂纹萌生过程视作损伤累积过程，基于连续损伤力学建立了损伤累积模型。结合360℃、650℃下G H 4169合金的低循环疲劳寿命数据拟合出模型的具体表达式，进而开展了对低循环疲劳裂纹萌生寿命的预测试验。结果表明：该方法针对G H 4169合金低循环疲劳裂纹萌生寿命的预测结果较为理想，其分散带基本在2倍以内，且能很好的反映变幅加载对G H 4169合金低循环疲劳裂纹萌生寿命的影响。

低循环疲劳；裂纹萌生寿命；G H 4169合金；连续损伤力学；航空发动机

0　引言

疲劳寿命问题一直是航空航天领域的难题，国内外学者对此进行了大量研究，并通过大量试验不断建立和验证疲劳寿命模型。在航空发动机疲劳问题中，低循环疲劳损伤占有重要地位，一旦发生在关键部件上将会造成极大影响。

高温合金在先进航空发动机上的用量占总材料的40%～60%［1］，主要是铁基、镍基和钴基高温合金［2-3］。其中GH4169合金是比较典型且应用较广泛的沉淀硬化型高温合金。由于其在650℃以下拥有塑性好、屈服强度高等优点，在航空发动机中主要用于制作涡轮盘、叶片等关键结构部件［4］。所以，准确预估其低循环疲劳寿命是很必要的。

目前，对于材料低循环疲劳裂纹萌生寿命的预测，被广泛应用的是Manson［5］与Coffin［6］各自独立提出的材料疲劳寿命的经验关系式，即Manson-Coffin方程，揭示了塑性应变幅和疲劳寿命之间的经验关系；很多学者对Manson-Coffin方程提出了修正公式，如：Morrow［7］于1965修正的总应变幅与疲劳寿命之间关系的方程。

基于这些方程虽然可以对材料低循环疲劳裂纹萌生寿命进行预估，但其主要基于经验关系，对拟合数据有很大的依赖性，导致在低循环疲劳寿命中高循环数范围的寿命预测结果精确度较低，不能很好满足实际的工程需要。而连续损伤力学中把材料所有的疲劳破坏过程都看作内部损伤的累积，结合热力学原理可以通过严密的理论推导来建立损伤累积模型来描述材料的损伤过程，模型中各参数物理意义较明确且减少了对数据的依赖性，通用性更强。

本文基于连续损伤力学的原理，将材料的循环软化视作损伤，把疲劳裂纹萌生过程看作材料内部的损伤累积过程。又以GH4169合金单轴拉伸疲劳的试验数据［8］进行拟合，建立了GH4169合金的低循环疲劳损伤累积模型，进而对其低循环疲劳裂纹萌生寿命进行预测。

1　低循环疲劳损伤累积模型

1.1损伤模型的建立

根据热力学定义：在等温过程中，封闭系统对外作功小于或等于系统Helmholtz自由能的减少量。所以，对于等温无穷小变形（无热量交换）过程，Clausius-Duhamel不等式可表示为

式中：σij为Cauchy应力张量为无穷小应变张量；为Helmholtz自由能密度的变化率［9］。

假设材料在损伤过程中具有弹性和各向同性，则Helmholtz自由能又可看作应变能。定义标量损伤变量，其中E为材料的弹性模量，E'为损伤后的弹性模量。当忽略其它变量，只用D和εij来描述损伤状态时，Helmholtz自由能密度可以表示为

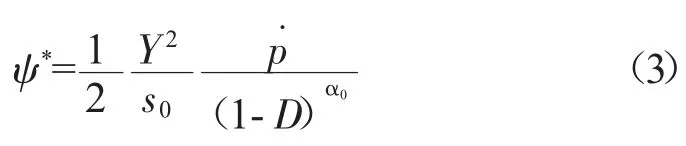
设

其中2个内变量σij和Y分别为εij和D的对偶变量，根据内变量的正交流动法则［9］，Lemaitre提出损伤演化方程［11］为

其中Helmholtz自由能密度对D的释放率Y表示为

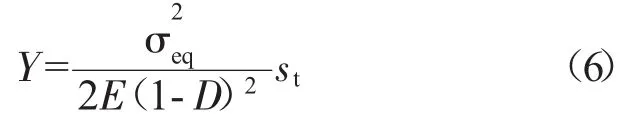
其中3轴因子st表示为

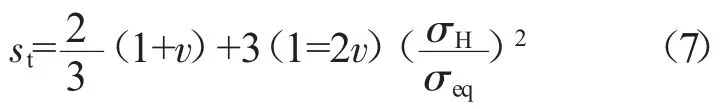
式中：σH为静水压力；σeq为Von Mises等效应力；v为泊松比。

联立式（3）、（5）和（6）可以得到损伤演化方程

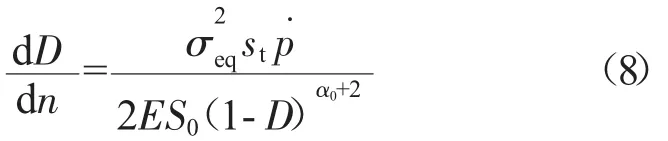
对于单轴拉伸的情况，σeq=σa，σa为应力幅，所以st=1。

材料在受到循环载荷时，往往会发生循环硬化和循环软化的现象。对于低循环疲劳，连续损伤力学中将累积塑性变形看作损伤形成的主要原因，而循环软化会随着累积塑性变形的增大而发生，并影响累积塑性变形变化率。所以，可以把材料的循环软化看作疲劳损伤过程［12］。稳定的循环软化过程通过通用的金属循环应力-应变关系来描述

式中：k'为循环强度系数；n'为循环硬化指数。式（9）等号右半部分别为循环软化稳定时每循环的弹性变形和塑性变形，塑性变形部分通过对应力幅求导可以得出累积塑性变形变化率

假设循环加载为比例加载，且每个循环过程中损伤程度不变，可以通过对式（8）进行积分得到损伤累积模型。由D的定义可知，在材料无损伤时，D=0；低循环疲劳裂纹萌生时，D=1［13］。对于GH4169合金，从开始受载荷到稳定循环软化阶段，通常为十几至几十个循环［12］。由于其低循环疲劳寿命很短，这个阶段可以忽略，把低循环疲劳裂纹萌生过程近似看作稳定循环软化过程，则可得到材料低循环裂纹萌生寿命方程

1.2变幅加载下低循环疲劳裂纹萌生寿命的预测

式（12）确定的是在等幅加载下的低循环疲劳裂纹萌生寿命。而实际工程中，材料往往在多级载荷的作用下造成损伤。

假设材料受到2级载荷，第1级载荷应力幅为σa1加载了N1循环，然后又在应力幅为σa2加载了n2循环直至断裂破坏。当上述2种载荷单独加载对材料造成相同损伤值时存在

式中：N2=Nf2-n2；Nf1、Nf2分别为2个载荷单独加载时对应的低循环疲劳裂纹萌生寿命，整理得

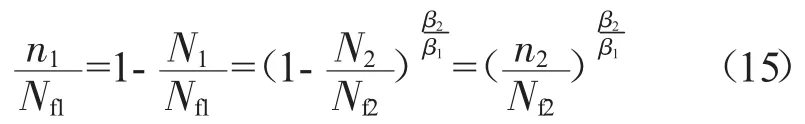
假设σa1＞σa1，当时，；反之，。这样可以根据不同材料β的不同，判断变幅加载对低循环疲劳裂纹萌生寿命的影响。

2　GH4169合金低循环疲劳损伤参数确定

2.1等幅加载条件损伤参数确定

从材料手册［8］获得GH4169合金在360℃和650℃下的数据，相关的材料参数见表1。其中E为弹性模量，k'为循环强度系数，n'为循环硬化指数。GH4169合金在2种温度下光滑试样循环疲劳试验数据见表2。

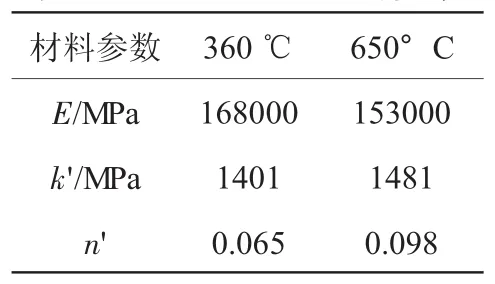
表1　GH4169合金的参数

从表1中可见，采用式（12）确定低循环疲劳裂纹萌生寿命时，还需要确定s0和β。s0为材料系数，取值通常为0.40～0.45，本文取s0=0.42［14］。材料的损伤累积过程主要受加载应力幅的影响，所以可以把β看作是应力幅σa的函数，通过表2中的数据进行拟合并确定β的表达式。GH4169合金在2种温度下β的拟合曲线如图1、2所示。用指数函数、幂函数、多项式函数、傅里叶函数等常用函数的β值拟合结果与GH4169合金在2种温度下的试验数据的β值进行对比，可得出指数函数和幂函数对β值的拟合结果最优。拟合参数的计算结果见表3。

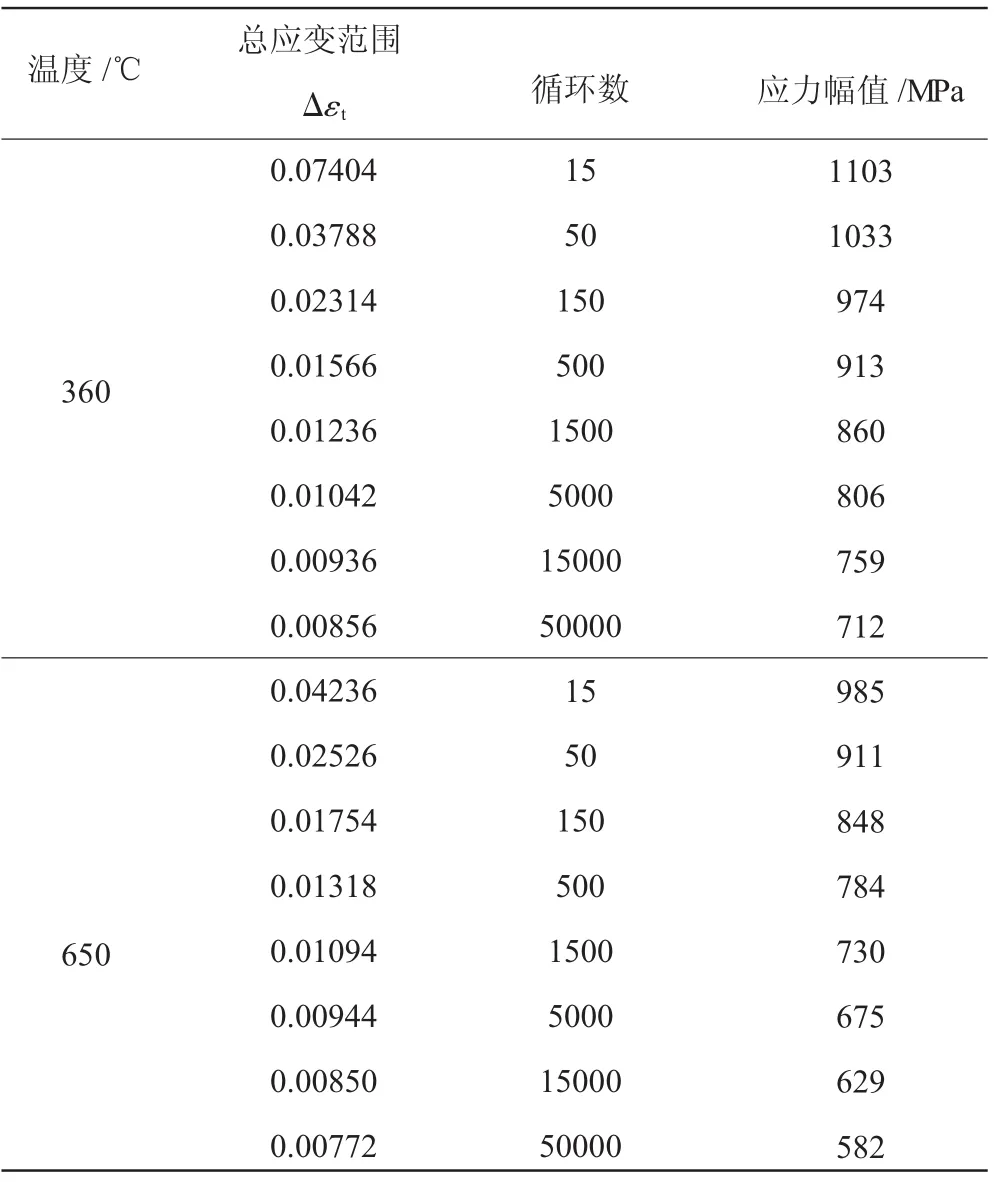
表2　2种温度下GH4169合金光滑试样疲劳试验数据

图1　360℃下GH4169合金的β拟合曲线

图2　650℃下GH4169合金的β拟合曲线

从图1中可见，在360℃下，GH4169合金的3种拟合效果比较接近，在高载荷情况下指数函数拟合更优；在低载荷情况幂函数拟合更优。从图2中可见，在650℃下，GH4169合金的3种拟合效果几乎与试验数据所计算的β一致。由于低载荷情况下误差对材料寿命影响较大，并考虑到公式的简捷性，将β的表达形式修改为

表3　2种温度下GH4169合金β的拟合结果

2.2变幅载荷对GH4169合金低循环裂纹萌生寿命的影响

上文中，β是通过等幅加载时的试验数据确定的表达式。当GH4169合金受2级变幅载荷加载时，假设σa1＞σa2，由前文知。根据式（12）、（16）得出此时Nf1＜Nf2，则n1＜n2，裂纹萌生寿命比等幅加载时长；反之，σa1＜σa2时，裂纹萌生寿命会缩短，如图3所示。

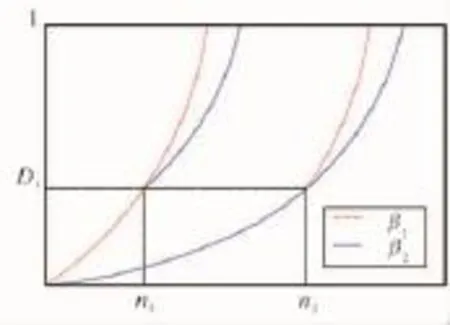
图3　载荷次序对损伤变量的影响

当材料受2级载荷加载时，假设应力幅σ1＞σ2，对于GH4169则β1＜β2。在造成相同损伤变量D1时，互换载荷幅值，从图3可见，变幅载荷由高到低的萌生寿命小于载荷由低到高的萌生寿命；等幅加载载荷为低载荷的萌生寿命最长，高载荷的萌生寿命最短，符合实际情况，体现β的表达式的合理性。

3　GH4169合金低循环疲劳裂纹萌生寿命预测

为了验证本文提出的损伤累积模型的预测精度，选取材料手册［8］中的方锻材和直接时效的GH4169合金涡轮盘锻件的试验数据进行拟合，数据见表4。由于疲劳模型只有2个未知参数，采用最小二乘法进行拟合，拟合参数值见表5。分别用式（12）和材料手册中拟合的Manson-Coffin公式进行计算，并对比预测结果，对比情况如图4、5所示，拟合结果见表6。

表4　2种温度下GH4169合金试验数据

表5　GH4169合金的参数拟合结果

图4　360℃下GH4169合金2种预测结果对比

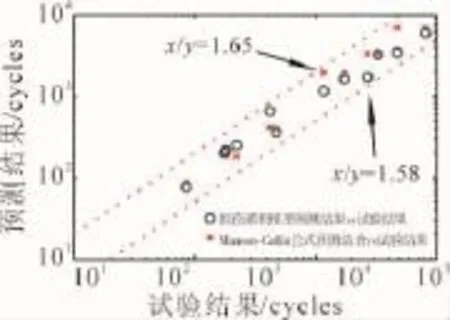
图5　650℃下GH4169合金2种预测结果对比

在图4、5中，X轴为试验寿命，Y轴为计算得到的预测寿命。从图中可见，采用本文方法计算得到的GH4169合金在2种不同温度、试样种类的情况下的低循环裂纹萌生寿命预测结果在较大范围内与试验数据十分贴近，基本都在2倍分散带以内，且在高于103循环数时比手册的结果更保守。从表6中可见，本文方法比材料手册［8］应用Manson-Coffin公式得到的残差平方和更小，对于方锻材试样，本文方法得出的残差平方和仅为Manson-Coffin公式的1.1%；对于涡轮盘锻件，残差平方和为Manson-Coffin公式的98.59%。综上，本文方法计算精度更高，满足当前工程的需要。

循环数　Δεtσa/损伤模型1.1487E4 1.8347E5 6.1009E5 9.8182E5 Manson-Coffin公式1.0884E4 1.7022E5 5.6195E5 9.0040E5试验1E4 2E5 5E5 10E5 0.8749E-2 0.705E-2 0.6498E-2 0.6295E-2 MPa 640 535 495 480

为了进一步验证本文方法在104循环数及其以上范围内寿命预测的准确性，采用前文650℃下GH4169光滑试样的补充数据［15］进行计算并与Manson-Coffin进行公式对比，结果见表7。

本文方法得到残差平方和为1.2726E10，而采用Manson-Coffin公式得到的残差平方和为1.4645E10，前者是后者的86.9%。结合表7可知，在相对低载荷的情况下，本文的低循环疲劳裂纹萌生寿命预测精度较高，误差相对更小。

表7　650℃下光滑试样高循环疲劳预测寿命

4　结论

（1）基于连续损伤力学建立了低循环疲劳损伤累积模型，并结合模型中参数与应力幅的关系和试验数据确定了拟合效果最优的低循环裂纹萌生寿命的表达式。

（2）预测的GH4169合金低循环疲劳裂纹萌生寿命结果均在2倍分散带以内，与Manson-Coffin公式相比，在循环数高于103时的预测精度更高。

（3）所建立的低循环疲劳损伤累积模型可以较好地反映变幅加载对低循环疲劳裂纹萌生寿命的影响。

［1］鲁凤鸣，金槿秀.GH4169合金涡轮盘件长期时效组织稳定性的研究［J］.金属学报，2005，31（7）：14-16.

LU Fengming，JIN Jinxiu.Study on long-term aging organization stability of GH4169 alloyturbine disk［J］.Acta Metallurgica Sinica，2005，31（7）：14-16.（in Chinese）

［2］Andersson H，Persson C，Hansson T.Crack growth in IN718 at high temperature［J］.InternationalJournalofFatigue，2001，23（9）：817-827.

［3］Burger J L，Biederman R R，Couts W H.The effects of starting condition on the aging response of as-forged alloy 718［C］//Proceedings of the International Symposium on the Metallurgy and Applications of Superalloy 718.Tms，1989：207-217.

［4］Sundararaman M，Mukhopadhyay P，Banerjee S.Precipitation and room temperature deformation behavior of Inconel 718［C］//Proceedings of the International Symposium on Superalloys 718，625，706 and Various Derivatives S.Tms，1994：419-440.

［5］Manson S S.Behavior of materials under conditions of thermal stress ［M］.Washington：NACA，1953：636-670.

［6］Coffin L F.A study of the effect of cyclic thermal stresses on a ductile metal［J］.American Society of Mechanical Engineers，1954，76：931-950.

［7］Morrow J D.Cyclic plastic strain energy and fatigue of metals［R］. ASTM STP 378，1965.

［8］中国航空材料手册编辑委员会.中国航空材料手册［M］.北京：中国标准出版社，1988：323-359.

Editorial Board of China Aeronautical Materials Handbook.China aeronautical materials handbook［M］.Beijing：China Standard Press，1988：323-359.（in Chinese）

［9］刘新东，郝际平.连续介质损伤力学［M］.北京：国防工业出版社，2011：180-210

LIU Xindong，HAO Jiping.Continuum damage mechanics［M］.Beijing：National Defense Industry Press，2011：180-210.（in Chinese）

［10］Deguang S，Weixing Y.Study on nonlinear continue damage cumulative model for uniaxial fatigue fatigue［J］.Acta Aeronautica et Astronautica Sinica，1998，19（6）：647-656.

［11］Lemaitre J.Evaluation of dissipation and damage in metals submitted to dynamic loading［J］.Mechanical Behavior of Materials，1972，76 （6）：540-549.

［12］魏大盛，王延荣，王相平，等.基于应力循环特征的裂纹萌生寿命预测方法［J］.航空动力学报，2012，27（10）：2342-2347.

WEI Dasheng，WANG Yanrong，WANG Xiangping，et al.Life prediction method based on characteristic of cyclic stress［J］.Journal of Aerospace Power，2012，27（10）：2342-2347.（in Chinese）

［13］Rabotnov Y N.Paper 68：On the equation of state of creep［C］//Proceedings of the Institution of Mechanical Engineers.Los Angeles：SAGE Publications，1963：2117-2122.

［14］Liu N，Gong Z，Tang Y，et al.A study on fatigue damage accumulation based on continuum damage mechanics［C］//Quality，Reliability，Risk，Maintenance，and Safety Engineering（ICQR2MSE）.Chengdu：IEEE，2012：867-870.

［15］王延荣，李宏新，袁善虎，等.确定总应变寿命方程参数的一种方法［J］.航空动力学报，2014，29（4）：881-886.

WANG Yanrong，LI Hongxin，YUAN Shanhu，et al.A method for determination of parameters in total strain life equation［J］.Journal of Aerospace Power，2014，29（4）：881-886.（in Chinese）

（编辑：栗枢）

Prediction of GH4169 Low Cycle Crack Initiation Life Based on Damage Mechanics

CHU Jin-yang1，HU Dian-yin1,2，MAO Jian-xing1，WANG Rong-qiao1,2，SHEN Xiu-li1,2

（1.School of Energy and Power Engineering，Beihang University；2.Collaborative Innovation Center for Advanced Aero-Engine，Beijing 100191，China）

In order to predict the low cycle fatigue crack initiation life of high temperature materials，the low cycle fatigue crack initiation life was regarded as a process of damage accumulation and a damage accumulation model was established based on the continuum damage mechanics.Parameters for low cycle fatigue life of GH4169 alloy at the temperatures of 360℃and 650℃were fitted to obtain the definite expression of the model，and low cycle fatigue crack initiation life predictions test were carried out.The results show that the low cycle fatigue crack initiation life used by the approach gives better estimation within about twice of scatter band for GH4169 alloy and a definite influence of variable amplitude loading on the low cycle fatigue crack initiation life of GH4169 alloy can be greatly reflected.

low cycle fatigue；crack initiation life；GH4169 alloy；continuum damage mechanics；aeroengine

V 232.3

A

10.13477/j.cnki.aeroengine.2016.02.017

2015-07-20基金项目：国家自然科学基金（51305012）、航空科学基金（2014ZB51）资助

初金阳（1990），男，在读硕士研究生，研究方向为航空发动机结构强度；E-mail：1129388292@qq.com。

引用格式：初金阳，胡殿印，毛建兴，等.基于损伤力学的GH4169合金低循环裂纹萌生寿命预测［J］.航空发动机，2016，42（2）：88-92.CHUJinyang，HU Dianyin，MAOJianxing，etal.PredictionofGH4169lowcyclecrackinitiationlifebasedondamagemechanics［J］.Aeroengine，2016，42（2）：88-92.