华应龙：阅兵中的数学故事

华应龙：阅兵中的数学故事

【编者按】

2015年9月3日，纪念中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵式在北京举行。铭记历史，展我军威，回首这次阅兵式，很多精彩画面仍然历历在目，激动人心。而著名特级教师、北京第二实验小学副校长华应龙更是从中发现了很多有趣的数学问题。2016年1月9日，在成都举办的第二届全国小学 “成长课堂”高峰论坛上，他带领电子科技大学附小六年级四班的学生，一起探究了这些问题。

时间：50分钟

执教：华应龙

学生：电子科技大学附小六年级四班

华应龙：

特级教师、北京第二实验小学副校长、北京教育学院兼职教授，著有《我这样教数学》《我就是数学》《个性化备课经验》等著作。

师：翻开新的一页，请在这一页的最上面写上你的名字。一个字大约一平方厘米左右，一平方厘米是多大呢，看看你是否心中有数。太小我就看不清了，如果你的名字中某个字我可能会读错，请你帮我注上拼音，老师一样会错的。

（教师和学生个别交流，念出学生的名字，“有的同学太好了，怕我不认识，三个字都注了音”。）

可以上课了吗？今天上课可以用计算器。至于什么时候用，我就不提醒你了。有人6+6也用。（学生笑）嘿嘿，真有人用的。好的，上课。

（师生互相问候）

上课可以笑嘛？觉得可以笑的点头，不可以笑的摇头。学校学校，学习怎么笑。所以你们会心的一笑，老师非常期待。刚才你们自发的笑声就非常可爱。刚才我跟大家说，有好多好玩的数学故事，今天这堂课我们来分享这三个故事。

第一个故事是“破解51之谜”；第二个，“为了神圣的那一刻”；第三个是“当坦克踩上俄军的脚跟”。这三个故事听完了，你再看阅兵的时候，感觉会不一样。你相信吗？我们拭目以待。

一、破解51之谜

师：第一个故事是破解51之谜。

（展示PPT：这次阅兵徒步方队有三个新亮点：一是每个英模部队方队掌7面抗战时期功勋荣誉旗；二是增加了20名将军领队，都是现职军职领导干部；三是三军仪仗队派出51名女仪仗队员首次参加受阅。）

孩子们，看完这段文字，你能发现和提出问题吗？看不见可以离开座位找个好的角度看。发现问题了吗？

生：破解51之谜，这里说有51名女仪仗队员，所以我觉得，第一个问题可能跟女仪仗队的队员有关。

师：刘昕宇，是我的托儿。（学生笑）对的，51名女仪仗兵怎么排？怎么会是51名？你想象一下。

生：我认为51可以分解质因数，它应该分解出来是17×3，那么我们就可以排17列3排，或者是3列17排。

师：哈哈，速度还挺快，掌声给她。还有不同的排法吗？

生：我觉得可以1个人在前面领队，然后后面50个人来排。

师：50个人怎么排？

生：或者一排10个，排5排，或者一排5个，排10排，还有很多。

师：那你觉得哪种更合适些？一排5个还是一排10个？

生（齐）：一排10个。

师：呵呵，行。还有不同的排法吗？

生：可以这样子，前面有两个人领队，七七四十九，一排七个人。

师：行不行？真好！还有其他的，不说了。到底是怎么排的呢？阅兵的时候……（展示图片）哦，找到答案了。现在你知道了，51名女仪仗兵是怎么排的。跟同桌交流一下。（学生交流）好了，现在谁来说，51名女兵怎么排的？来，小伙子。

生：三军仪仗队每排是17个人。三军仪仗队是海、陆、空，每排代表一个兵种。三个兵种一共就是51个人。

师：对呀，整个仪仗兵就是一个方队，后面跟着的是10个英模部队方阵。男兵和女兵是一个方阵，一共12排，女兵是3排，还有9排是男兵。一看颜色就分得很清楚了。就像刚才我们同学所说，三军仪仗队，陆、海、空，明白了？

后来我又想，怎么会是一排17个人？不是好事成双，一排18个人多好？你觉得呢？带着一系列的问题，我就去请教了北京军区阅兵的指挥官。张部长给了我两大张数据，让我很惊讶。阅兵中有这么多数据呢。三军仪仗队——

生（齐）：17×12+3！

师：对，就是刚才我们解读出来的。眼睛快的人还发现一个式子。（学生思考，小声回答）对，英模部队方队——25×14+2+7。看到这个式子，你能想到什么？

生：我想到了可能有两个将军在带队，然后有七个掌旗的。其余的25×14是他们的那个小兵，跟着将军后面的小兵。

2015年12月9日，华应龙在砂子塘泰禹小学讲授“阅兵中的数学故事”。

（学生笑）

师：嘿嘿，这个成都话说出来特别的可爱。是这样的吗？

生：是。

师：给他掌声！解读得非常好。是呀，刚才我们就纳闷，一排怎么会是17个人，现在又怎么会是一排25个人？怎么都是单数呢？为什么？你有没有想法？

（没有学生回答）

师：当时我也是百思不得其解，因此我就请教张部长。张部长告诉我，单数就有一个人是在正中间。整个队伍从前面看上去，就有左、中、右的对称的美。双数也对称，但是没有一个人在中间了。前面7面旗帜，也是有一个在中间，是面大旗。

从刚才的交流，让我们想到了一个成语，叫“一叶知秋”，一片叶子落下来就知道秋天到了。一个数据也能带给我们很多的想象。只要我们去想象，就会破解出很多的谜底。

二、为了神圣的那一刻

师：阅兵中踢正步通过检阅区的那一刻，无疑是神圣的，是震撼的。那一刻是多长时间呢？大家在课前收集资料的时候注意到了，这次阅兵，时间上不允许超过0.3秒，距离上不允许超过0.02米，是特别的苛刻，要求特别的严。我想，阅兵指挥官是一定要知道，一个方队通过检阅区的时间到底是多少秒。你觉得是不是要解决这个问题？肯定要。那现在你想想，如果要知道这个方队通过检阅区需要多少秒，得知道什么数据？四个人先交流。（学生交流半分钟后）来，女孩先说。

生：首先要知道路程。

师：就是检阅区的长度。

生：然后要知道速度，然后，路程除以速度等于时间。

师：要知道检阅区长度，还要知道速度。还有谁要补充？来最后一个男孩。

生：还要知道他们方队的长度。

（学生鼓掌）

师：赢得了一片掌声。还要知道方队的长度。检阅区的长度是多长？有没有人知道？是天安门前东西两个华表之间的距离，96米。有没有同学来做个老师讲一讲，为什么要知道方队的长度？

生：因为如果一个方队的第一排过了检阅区，还不能算整个方队过了检阅区。要整个方队的最后一排过了检阅区，才算整个方队过了检阅区。所以要算方队的长度。

（学生鼓掌）

师：好。还有没有不同的角度，用上我们以前所学的知识？来回答我们这个问题。

生：这个和火车过桥的问题一样，要知道速度和时间，还有路程。

师：他说的对不对？这是个什么问题？

生（齐）：火车过桥。

师：也是我的托儿。还记得这个图吗？（出示教材上火车过桥问题的图片）对，这就是火车过桥问题。要解决火车通过这个桥需要多长时间，我们就要知道桥长，还要知道车长。火车的长度在这道题里面就是方队的长度了。好。孩子们，那现在给你这些数据，就是张部长给我的这些原始数据，你能算出方队的长度吗？能不能一边读，在脑子中想象出一个线段图，这个方队的长度是怎样的？来，我们一起读。

（学生一边读，老师一边用PPT逐步出示线段图）

生（齐）：旗手脚尖到将军脚尖6米，将军脚尖到第一排脚尖6米，后面14排都是前一排脚跟到后一排脚尖0.9米，脚长0.3米。

师：这张图是不是跟你想的一样？那现在看着这张图，你能不能很快地计算出方队的长度？从前到后一共是多长？自己来，独立完成。注意，用计算器的同学把声音关了，式子还是要写下来，不然就只有结果，看不到过程。

六4班同学非常棒，我看了两圈，大部分同学都有答案了，反应真快，不过，就是答案都不一样。现在可以离开座位，带着你的思考，找你的好朋友交流一下，这个问题到底怎么算？

（学生交流）

刚才我在这里欣赏科大附小六4班的同学，非常美，讨论的习惯很好。开始大家纷纷表达自己的想法，达成一致了，就安静下来，回到自己的座位。真美！哪位同学想和大家一起分享？（学生纷纷举手）来，请开始想错了，现在明白了的说。

生：我写的算式是（0.9+0.3）× （14-1）+12。我是这样想的，因为旗手和将军很简单，主要在士兵上有很大的差异，所以我就画了很多的士兵。这里有三个士兵，前一排脚跟到后一排脚尖的距离是0.9米，还有0.3米的脚长，所以把0.9和0.3加起来。后面乘以14减1。三个人中间就有两个1.2，比人数少了一个1.2。所以我就把它带到算式里去就要减1，12就是旗手和将军两个人的长度。

师：你是开始就这么想的？

生：是交流了以后我发现我把0.9+0.3算成1.1，应该等于1.2，然后就改了个答案。

（学生笑）

师：哈哈哈，啊，有交流就有收获。听了她的发言，还有补充的吗？

生：我认为这个答案不对。虽然三个人有两个1.2，但是他前面这里有个0.3是没有算过的，所以说我认为这里还要加上一个0.3。

（学生鼓掌）

师：刘昕宇同意吗？

生：我同意张文洁的看法。

师：为什么还要加一个0.3？哪位能够做老师再讲清楚？

生：因为他总共有14排士兵，每个士兵都有一双脚，总共有14个0.3，所以减1之后还必须要加一个脚长。

师：同意吗？其实用数学的语言，0.9和0.3是一一对应的，前面这个0.3还没有0.9来对应，所以要加一个0.3.那么答案是多少？27.9米。刚才昕宇写的这个式子，14减1是为什么？谁能用以前学的知识来解答？

生：这个问题就跟我们以前学过的植树问题一样，14排我们就看成是14棵树，这个问题就等于两旁都栽，那么0.9就等于他们中间那个段的长，14减1就是他们中间一共有多少段，就是有多少个间隔。

（学生鼓掌）

师：你是我的知音。是的，5棵树几个间隔？

生（齐）：4个。

师：那现在14排士兵多少个间隔？

生（齐）：13个。

师：所以只有13个0.9。还有没有不同的算法？谁来说？

生：（0.9+0.3）×（14-1）+12+0.3+0.3+0.3。结果是28.5。

师：我刚才看的时候发现很多人都是这个答案。

生：因为刚才那个只算了14排士兵和他们的距离，将军的脚和旗手的脚都没算。

师：很好，我们魏萧逸，首先给他掌声，他勇于表达自己的见解，非常好！那现在，和上一个式子一比，我们知道后面多加了两个0.3，萧逸的理由是将军和旗手的脚长没算。

生：我们看第一个语句，旗手的脚尖到将军的脚尖，说明这一段的6米是加了旗手的脚长，第二个语句，将军的脚尖到第一排的脚尖，这里的6米也是算了将军的脚长，所以我觉得后面两个0.3可以去掉。

（学生掌声）

生：哦，我知道了。我同意他的看法。

师：真好，通过和萧逸同学的一番对话，让我们知道咬文嚼字地去审题太重要了，就因为咬文嚼字，就发现这个0.3是包括在里面的。我们给掌声。开始不明白就勇于坚持自己的观点，明白了就修正、接纳，真好！

还有没有不同的做法？刚才我看了一圈，发现大多数人都写出了答案，但还有一些人没有写。是不是？肯定是这道题目碰到难处了，怎么这么繁啊？我们在课本上没做过这么繁的题目。对这些同学，如果要帮助他们的话，你要怎么告诉他们？

生：我觉得可以分段来做。把这道题拆成三个问题，从旗手到将军是6，将军到士兵也是6，然后再算14排士兵的距离，最后再加起来，就容易得多了。

师：好，后面有同学跟你互动。

生：首先我赞同他的意见，把问题分成几段去做，先是6乘2，重点是后面那段，类似于植树问题有点难。脚长是0.3，每排相距0.9。这个0.9就相当于植树问题的段数，间隔。我们把段数算出来，乘以0.9；把棵数算出来，乘以0.3，最后把12米加起来。我觉得这个方法还是比较简单的。

师：明白了？对的，这其实是分类在算。有几个6？（2个），有几个0.9？（13个），有几个0.3？（14个）。以后，碰到复杂的问题，自己没有思路的时候，可以先想，能不能分类啊？一分类6×2+0.9×13+0.3×14，这样加起来，整个从前到后的长度不重不漏，无缝连接，结果多少？27.9。

好了，孩子们，速度，方队的速度是多少呢？给你选择，是我告诉你，还是你自己把它算出来？（自己算）好的，厉害，愿意接受挑战。课前我们就知道了，这次阅兵节拍由之前的116拍变成112拍，112拍是什么意思？对，一分钟走112步。一步是多长？75厘米，那么你能不能根据这两个数据，算出速度，1秒钟走多少米？好，自己独立完成。

好，我们听听张敏杰怎么做的。

生：112乘以75再除以60等于140米每秒。

（有学生不同意，说是“1.4”。）

师：同意140米的举手。同意1.4米的举手。我看到敏杰写的140，我想，新的世界纪录诞生了。

（学生笑）

你知道100米全世界跑得最快的是谁？博尔特，博尔特100米跑多少？9秒58。现在，敏杰让我们阅兵的士兵140米跑一秒。（全班大笑）我们班老师肯定提醒过，注意单位名称。孩子们，错误都是提醒，掌声感谢敏杰提醒我们。

好了，孩子，整个方队的长度、检阅区的长度和速度都知道了，现在你能够计算出通过时间了吗？独立完成。比赛，看男同学全对的多还是女同学全对的多。

好，来，昕宇报一下算式。

生：（96+27.9）÷1.4=88.5（秒）

师：男同学跟昕宇一样的举手，16。女同学……我们班男生女生人数一样吗？（不一样）哦，那不比了。（同学们笑）看来大家都知道怎么去算，总路程除以速度就等于时间。我非常佩服地告诉你，同学们算出的答案跟阅兵指挥官的数据完全一致。

（学生鼓掌）

做完这道题，我又发现一个问题：旗手和将军、和第一排士兵的间隔为什么是6米，而不是7米？

生：六六大顺！

（学生笑）

师：是，这是一个很好的解读的角度，六六大顺嘛。还有没有其他的角度？孩子们，一个问题背后的答案往往不止一个。

生：我觉得看起来比较整齐，因为6米是双数。

师：还有没有其他的角度？

生：我想阅兵都是有时间限制的，如果距离长了时间就不够了。

生：我还有个想法，因为脚长是0.3米，如果是6米是20个脚，比较好量。

师：我觉得昕宇讲的角度还有启发。6米，一步是75厘米，算一算6米是跨几步呀？快用计算器算。

生：8步。

师：怎么算的？600除以75，很好。我们知道单位要统一是不是？如果是7米的话，是多少步呢？是不是除不开了？不是一个整步数了。中间间隔6米，第一排旗手踩着敬礼线了，然后将军还可以踩着那条线，第一排士兵也可以踩着线，因为他们中间是整步数。如果变成7米的话，第一排人踩到了，后面的人还能踩到吗？踩不到了。

孩子们，你们注意到了吗？阅兵的时候将军喊：向右看！那是四拍喊的，四拍喊完之后，再过四拍士兵就可以踩着线了。来，我们一起看看。我们打着节拍看脚步。

（放阅兵视频，狼牙山五壮士英模部队方队）

很好，同学们的节拍打得挺准的。孩子，我们打节拍看脚步，先看旗手的脚，然后再看将军的脚，然后看士兵的脚。再来一遍。

（再放一遍阅兵视频）

真好，都踩到了。这么一研究是不是认同大哲学家说的一句话：“哪里有数，哪里就有美。”

（学生鼓掌）

三、当坦克踩上俄军的脚跟

师：孩子们，当我从报纸上看到这次阅兵还有俄罗斯军队参加的时候，我就想到，我在俄罗斯红场看到俄军踢正步。他们的正步跟我们的正步大不相同，请看。（展示图片，学生笑）他们两腿之间的角度是90度到100度，我们两腿之间的角度是45度到60度。我们一步长75厘米，他们一步长80厘米。问题来了。

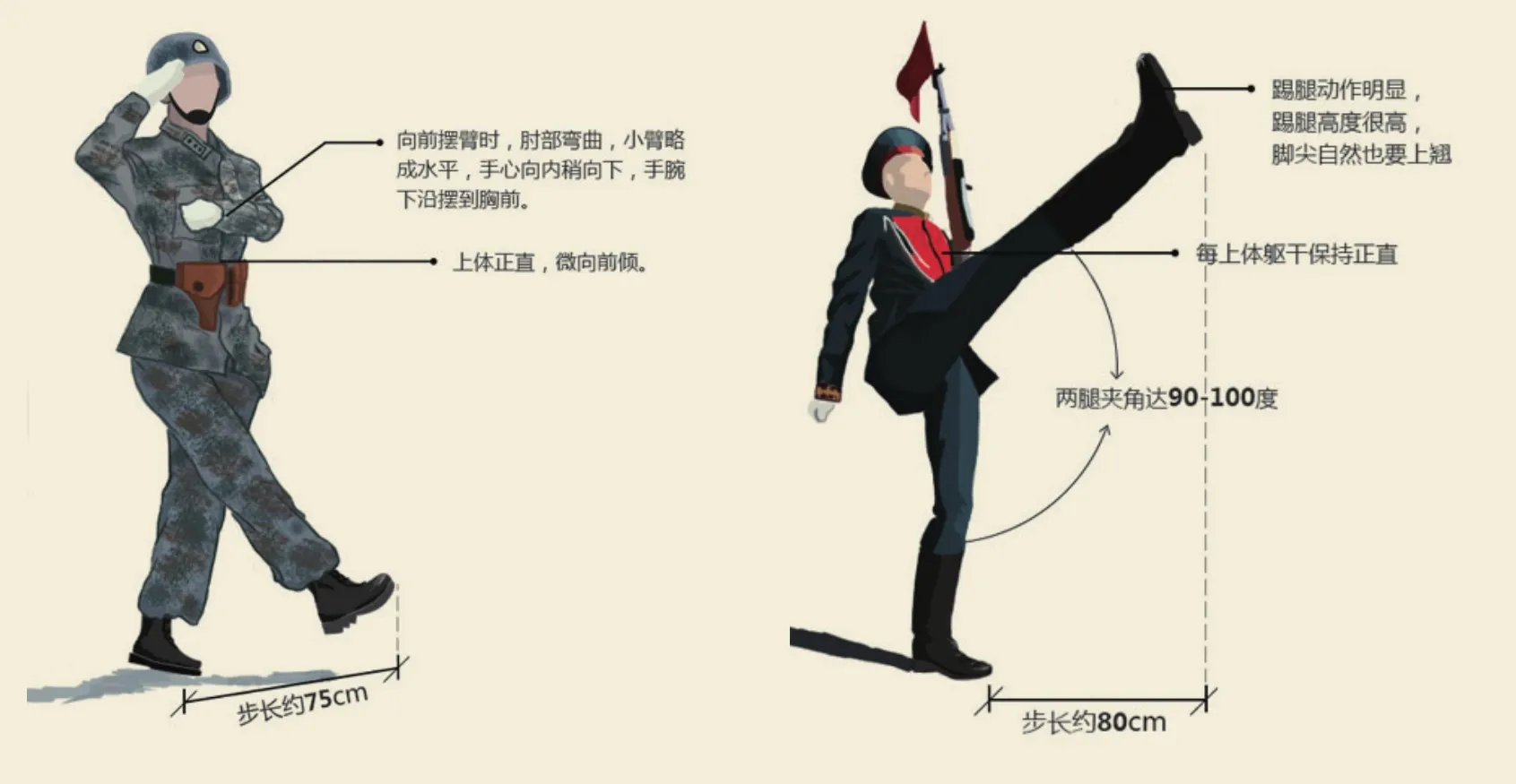
（展示PPT，中国士兵每步75cm，俄罗斯士兵每步80cm，假设每个方阵相距20米，俄罗斯方阵需多少秒钟追上中国方阵？）

（学生纷纷说是“追及问题”）

好了，我们不去算具体多少秒了。你知道这个问题在阅兵指挥官那是怎么解决的吗？请看屏幕。

（展示PPT：本次阅兵外军队伍按中国步伐标准受阅）

俄罗斯按照我们的步伐标准接受检阅的。一分钟112步，一步75厘米。这样还存在追及问题吗？不存在了。好的。那这次阅兵中就没有追及问题了吗？

有，还有坦克。俄军方队之后就是坦克方队，坦克方队的速度是2.78米/秒，想象一下会有什么事情发生？那怎么解决呢？

生：坦克放慢速度。

师：坦克放慢速度就不是坦克了，是蜗牛了。

生：俄军再加快速度。

师：他们又去踩人家了。

生：可以让坦克表演边转边走。

（学生笑）

师：增加一些活动？很好的主意……大家的数学感觉挺好。到底怎么解决这个问题，欲知后事如何，且听下回分解。好了，同学们，时间到了。今天这堂课我们一起分享了阅兵中的数学故事，回首这三个故事，你有什么收获？

生：火车过桥问题。

师：也就是我们以前在课本中学的问题，在今天解决了阅兵问题。有了用武之地。

生：我知道了可能在生活中一件很微小的事情中也有数学问题。生活处处有数学问题。

师：真好。叫什么名字？王文倩。马克思说了一句跟你类似的话，（展示PPT）一起读：

生（齐）：任何一门科学只有成功地运用数学的时候，才能达到真正完善的地步。——马克思

师：任何一门科学，任何地方都有数学。所以大哲学家培根也说过一句话。

生（齐）：数学使人精细。

师：你是不是感受到了这一点？有精细才有了美。好，还有什么收获？

生：华老师说有了数学才会有了美。我们在阅兵这个数学问题中对这句话有了深刻的理解。

师：真好！今天这节课学得开心吗？为什么呢？这就是孔子说的那句话：学而时习之，不亦说乎。我们前面学了，今天是在习，实际地练习。所以我们感到很高兴。

今天这堂课我们不断地在想象。数学是抽象的，学数学需要想象。想象了就好玩。好了，孩子们，其实上了这堂课，概括起来，我有一句话跟大家分享——

（展示PPT）

生（齐）：心中有数，无限美好。

师：你再看阅兵的时候，是不是能感受到这一点呢？

（再次播放阅兵视频，学生鼓掌，课程结束）

华应龙老师著作《华应龙与化错教学》，北京师范大学出版社2015年出版