一类多目标优化问题的凝聚同伦算法

贺　莉，李　娜，刘庆怀，王秀玉

(长春工业大学基础科学学院，吉林 长春 130012)



一类多目标优化问题的凝聚同伦算法

贺莉，李娜，刘庆怀，王秀玉

(长春工业大学基础科学学院，吉林 长春 130012)

利用凝聚同伦算法求解一类带有等式约束和不等式约束的多目标优化问题.首先用凝聚函数对等价转化后的不等式约束条件进行光滑逼近，然后给出相应的组合同伦方程，在广义弱拟法锥条件下，证明其解几乎处处收敛于该类多目标优化问题的KKT点.

多目标优化；凝聚函数；同伦内点方法

凝聚函数方法的思想起源于1979年Kreisselmeier和Steinhauser[1]得到的研究成果，20世纪80年代这种思想被广泛地应用于结构优化和工程设计等领域.[2-3]2000年于波等[4]把凝聚函数的思想与组合同伦内点方法结合起来，提出了凝聚约束同伦方法，并指出这种方法的主要优点在于大大降低了同伦路径数值跟踪时线性系统的维数，缩小了问题的求解规模.此后很多学者进行了深入研究，在解决极大极小问题、非线性规划问题和互补问题等方面取得了一些重要结果.[5-7]文献[8]给出了含有不等式约束的非线性规划问题的改进凝聚约束同伦方法，文献[9]把凝聚约束同伦内点方法推广到只带有等式约束的凸多目标优化问题.本文在文献[8-10]的基础上，通过引入正不相关概念，给出较弱广义弱拟法锥条件，在较弱的假设条件下，研究了一类既含有等式约束又含有不等式约束的多目标优化问题.

本文考虑一般多目标规划问题(MOP)

minf(x)，

s.t.gi(x)≤0，i∈M，

hj(x)=0，j∈L.

(1)

其中：x∈Rn；M={1，2，…，m}；L={1，2，…，l}；f=(f1，f2，…，fp)T：Rn→Rp；g=(g1，g2，…，gm)T：Rn→Rm；h=(h1，h2，…，hl)T：Rn→Rl；f，g，h均为三次连续可微向量值函数.引入以下符号：

Ω={x∈Rn|gi(x)<0，hj(x)=0，i∈M，j∈L} 表示严格可行集.

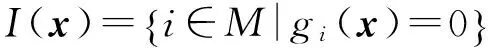
令

(2)

(3)

1　预备知识

定义1如果存在二次连续可微映射ηi(x，zi)：Rn+1→Rn(i=1，2，…，m)，∀x∈Ω满足：

(1)ηi(x，0)=0，i∈M；

本文假设：

上式是假设条件(A3)的特殊情形，因此本文广义弱拟法锥条件下求解多目标优化问题扩大了凝聚同伦内点方法的使用范围.

由于问题(3)是非光滑多目标优化问题，我们利用如下凝聚函数进行光滑化.

(4)

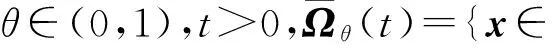
显然， 当t→0+时，问题(4)的解为多目标优化问题(1)的解.

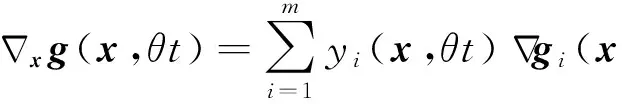
其中

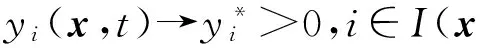
引理3[4]假设条件(A1)成立，则：

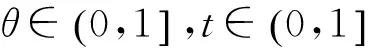
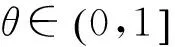
则

y=0，z=0，uj=0，j∈L.

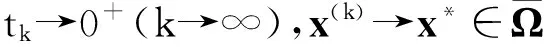
(5)

其中

这与假设(A3)矛盾，命题得证.

2　同伦方程的构造及同伦路径的存在性

为求解问题(4)，利用线性加权法将其转化为如下n+p个变量的非线性规划问题：

(6)

相应的KKT方程为：

(7)

称(x，λ)是MOP问题的KKT点，(y，u，v，h)是MOP问题的Lagrange乘子.对于凸多目标规划问题，其解可以通过求解KKT系统得到.对于非凸多目标规划问题，得到的是MOP问题的KKT点.

为求解KKT系统，构造如下组合同伦方程:

(8)

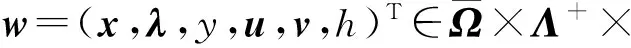
当t=1时，同伦方程(8)变为

(9)

当t→0+时，方程(8)的解为KKT系统的解，即为问题(1)的KKT点.

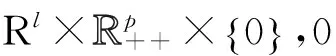
(10)

3　同伦路径的有界性和收敛性

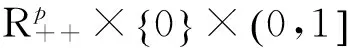
(1) 当h(k)→∞，v(k)→∞时的不可能性证明见文献[5].

(2) 若u无界，则‖u(k)‖→∞(k→∞)，由方程(8)第一式有

上式两边取极限得

上式若成立，则其极限必存在，记

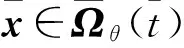
由方程(8)第一式有

η(x(k)，θtk，tk(1-tk)(y(k))2)+

(10)

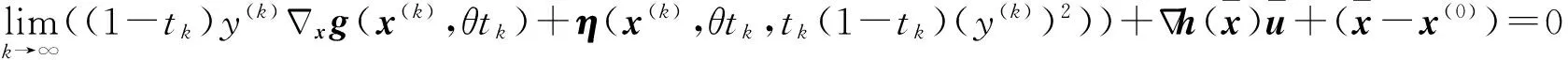
(11)

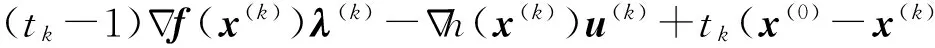
用Γw(0)的弧长s参数化该曲线，存在连续可微函数w(s)，t(s)， 满足

Hw(0)(w(s)，t(s))=0，t(0)=1，w(0)=w(0).

微分上式有：

定理4同伦路径Γw(0)可由下面常微分方程的初值问题确定：

t(0)=1;

w(0)=w(0).

且如果有t(s*)=0，则w*=(x(s*)，λ(s*)，y(s*)，u(s*)，v(s*)，h(s*))T是KKT方程的解.

[1]KREISSELMEIER G，STEINHAUSER R. Systematic control design by optimizing a performance index:Proceedings of the IFAC Symposium[C]. Switzerland：Zürich，1979.

[2]BARTHELEMY J F M，CHANG K J，ROGERS J L. Shuttle solid rocket booster bolted field joint shape optimization.[J]. Spaceraft and Rockets，1998，25：117-124.

[3]HAJELA P，Techniques in optimum structural synthesis with static and dynamic construints[D]. Palo Alto：Stanford University，1982.

[4]YU BO，FENG G C，ZHAGN S L. The aggregate constraint homotopy method for nonconvex nonlinear programming[J]. Nonlinear Analysis，2001，45：839-847.

[5]刘庆怀，林正华. 求解多目标规划最小弱有效解的同伦内点方法[J]. 应用数学学报，2000，23(2)：188-195.

[6]LIU GUOXIN. Aggregaye homotopy methods for solving sequential max-min problems，complementarity problems and variational inequalities[D].Changchun：Jilin University，2003.

[7]金鉴禄，王秀玉，贺莉等.约束序列极大极小问题的凝聚同伦内点方法[J]. 应用数学学报，2010，3(5)：792-804.

[8]SU MENGLONG，YU BO，WANG JIAN. Solving nonconvex nonlinear programming problems via a new aggregate constraint homotopy method[J]. Nonlinear Analysis，2010，73：2558-2565.

[9]杨轶华，赵立芹，吕显瑞等. 多目标凸规划凝聚同伦内点算法[J]. 吉林大学学报(理学版)，2006，44(6)：883-887.

[10]术洪亮，张春阳. 求解非凸优化问题的一种连续化方法[J].东北师大学报(自然科学版)，2012，44(3)：31-34.

[11]ALLGOWER E L. Numerical continuation methods：an introducation[M]. New York：Springer-Verlag，1990：114-115.

(责任编辑：李亚军)

Aggregate homotopy method for a class of multiobjective programming problem

HE Li，LI Na，LIU Qing-huai，WANG Xiu-yu

(School of Basic Science，Changchun University of Technology，Changchun 130012，China)

The aggregate homotopy method was used to solve a class of multiobjective programming problem with both equality and inequality constraints. The inequality contraints were deformed and smoothly approximated by aggregate functions. A general weak quasi-normal cone condition was defined in the feasible region and the corresponding homotopy equation was given. For almost all points in the feasible region，it converged to the KKT point of the multi-objective programming problem.

multiobjective optimization；aggregate function；homotopy method

1000-1832(2016)03-0041-07

2015-04-07

国家自然科学基金资助项目(51278065)；吉林省自然科学基金资助项目(20130101061JC).

贺莉(1970—)，女，硕士，教授，主要从事最优化理论与算法研究.

O 221[学科代码]110·74

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.009