一类无人机内外环编队的控制律设计

徐 清 严少波 刘彦生



一类无人机内外环编队的控制律设计

徐 清 严少波 刘彦生

本文主要是针对无人机（Unmanned Aircrafts）编队飞行控制（Formation Flight Control）进行研究。首先为无人机编队模型设计控制器，通过为编队模型设计的控制器保证编队模型输入—状态稳定。其次，针对无人机自身的线性模型设计控制器，并最终得到稳定的闭环系统，使得整个编队在飞行的过程中保持稳定。最后，通过Matlab仿真验证方法的可行性。

随着无人机技术的不断发展，无人机编队飞行也成为近年的研究热点。多架无人机为完成某项任务而形成的某种组织模式或队形排列——即无人机编队飞行。编队控制的方法目前大致可以分为长机—僚机（leader-follower），虚拟结构（virtual-leader）等。为了既能描述无人机编队内每架机的行为与飞行状态，也能反映无人机在自身控制器控制下的状态，本文结合了编队模型与无人机模型进行研究。本文将无人机编队模型划分为外环与内环两部分：外环模型即无人机编队模型，控制的是整个编队的飞行状态；内环模型则控制无人机自身的动态行为。对于外环编队模型的研究，主要通过分析编队内两架无人机之间前向位置误差与横向位置误差，来观察编队队形的维持与变化。而对于内环无人机模型的研究，则主要集中于无人机自身对称面内的纵向运动以及非对称面内的横向运动。

编队运动方程

考虑由q（ q≥2）架无人机组成的编队，使用leaderfollower拓扑结构，每架无人机只有一架参考机。无人机i 在编队内的运动学方程为：

其中vi表示前向速度，xi, yi表示无人机i 的位置，φi表示x 轴与vi之间的夹角，wi表示角速度。无人机编队控制，主要是分析研究每架无人机的位置和方向以及两架无人机之间的位置关系。而通过设计内环控制器的升降舵、油门、襟翼和副翼则可以跟踪vi和wi。

无人机之间的位置误差关系如图1所示，可以表示为：

对公式（2）关于时间进行求导，得到以下外环模型：

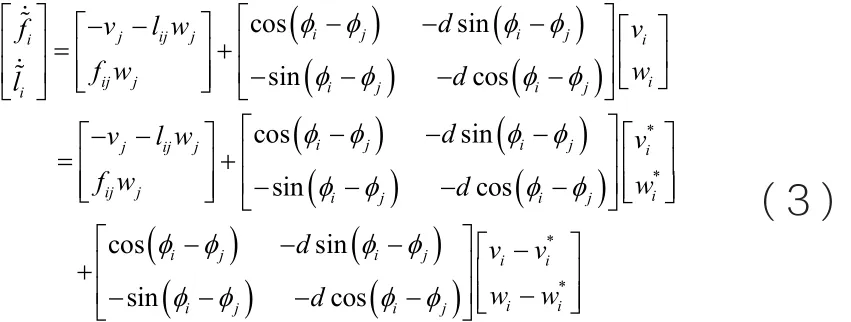
将vi和wi视作外环模型的输入，公式（3）中的则是理想的控制律。通过合理的设计

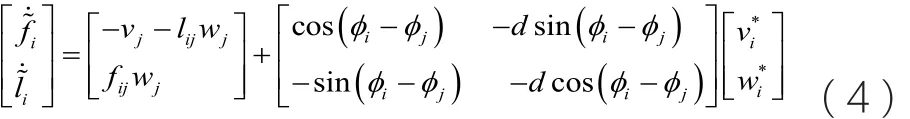
无人机内环模型

对编队内环模型进行控制，目的在于使得内环系统的速度与角速度跟踪上相应的外环信号。无人机线性系统的内环模型如式（5）所示：

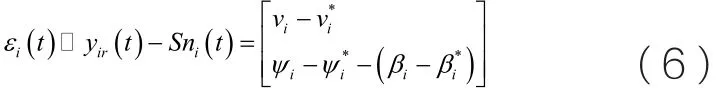
其中S∈ϑ2× 2是已知常数矩阵，是期望值。

上述增广系统可以简写为如下形式：

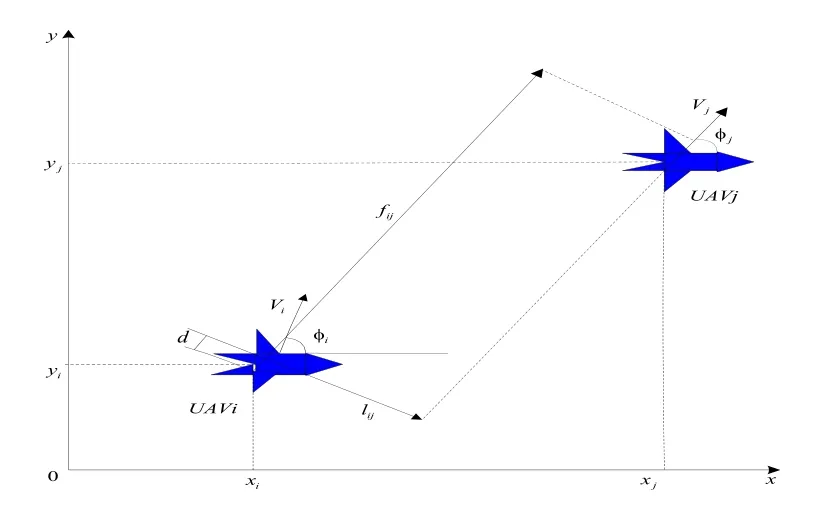
图1　编队结构位置关系

图2　五架无人机编队拓扑结构

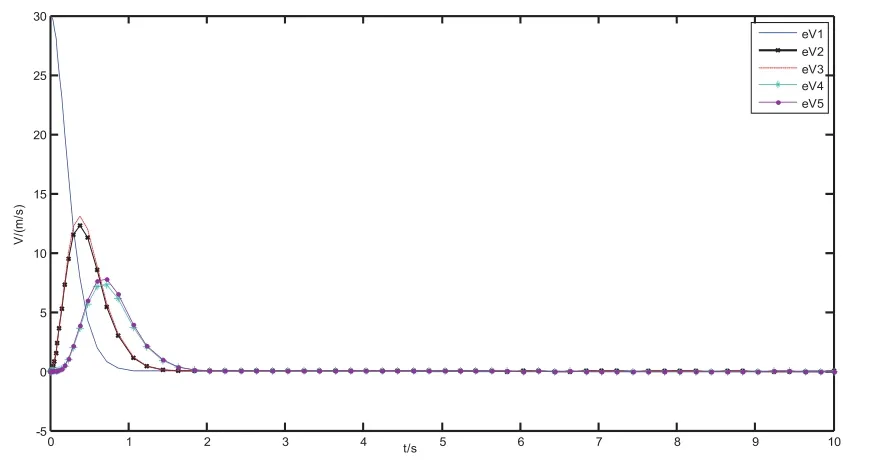
图3　速度误差曲线

图4　角速度误差曲线

，针对系统（8）设计如下反馈控制器：

引理1.1：给定常数γ，若存在对称矩阵Z ∈ϑ10× 10和矩阵W∈ϑ4× 10使得下列不等式（13）

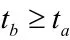
那么

定理1.1：如果存在对称矩阵Pi使得下列不等式成立：

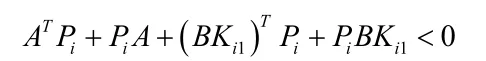
成立，那么误差ηi是指数稳定的并且mi是有界的。

仿真分析

运用Matlab/Simulink验证设计控制律的有效性。编队由5架无人机组成，拓扑结构如图2所示。编队的具体细节见参考文献。

期望速度与期望角速度分别为V*=30m/ s, w*=0.5rad/s 。对于内环变量ψ*=32deg/s,β*=6deg/s。系统矩阵采用如下形式：

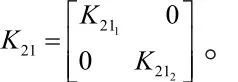
对于该无人机编队，速度与角速度误差曲线如图3，图4所示，误差均收敛于0。无人机编队能保持稳定飞行。

结语

本文主要通过内环与外环相结合的方式，实现了无人机编队飞行。通过设计的内环与外环控制器，使得整个编队稳定。实现了内外环结合后，可以考虑编队出现不同的故障时，如何重构编队控制来维持编队队形以及稳定的问题。

徐 清 严少波 刘彦生

上海飞机设计研究院

10.3969/j.issn.1001-8972.2016.11.011