引入陀螺观测量的捷联快速双位置对准方法

李　逸，杨孟兴，徐兵华

（中国航天科技集团第16研究所，西安710100）

引入陀螺观测量的捷联快速双位置对准方法

李逸，杨孟兴，徐兵华

（中国航天科技集团第16研究所，西安710100）

为了解决初始对准中速度与精度相矛盾的问题，提出了静基座下引入陀螺测量误差信息的捷联快速双位置对准方法。在常规对准方法基础上，增加陀螺测量角速度信息为观测量，提高系统可观测度，提升滤波器的收敛速度。针对双位置单滤波器方位失准角估计慢的问题，提出双位置双滤波器的对准方案。仿真验证表明，该方案方位失准角的估计精度与水平失准角相当。该方法切实可行，对提高惯导系统的可观测性和缩短对准时间，有重要的参考价值。

捷联惯导；卡尔曼滤波；双位置对准；可观测度

0　引言

在初始对准中，常用的方法是卡尔曼滤波，该方法对不可观测状态很难进行有效估计，从而制约了武器系统的精度与速度［1］。为了提高对准速度，文献［2］、文献［3］中将等效陀螺引入到对准过程中，加强对陀螺信息的利用，这个方法能加快对准速度，却不能提高精度，不利于提高武器命中率。为了提高对准精度，文献［4］、文献［5］中分别提出了多位置对准方法和连续旋转对准方法。目前捷联惯导系统采用传统的双位置对准方法，以速度误差作为观测量，整个对准过程采用一个卡尔曼滤波器［6］。由于转位运动、惯性器件误差的影响，滤波器收敛速度较慢，导致对准时间变长。

为了同时提高初始对准的速度与精度，本文提出了一种快速双位置对准方法，在两个位置分别采用两个卡尔曼滤波器进行状态估计，通过两个位置之间的空间关系列写方程组并求解各项误差参数，且将每段滤波过程中加入的等效陀螺仪测量信息作为新观测量，提高每个位置滤波器收敛速度。这样既能提高系统可观测性，又能保证系统快速性，最后通过仿真验证这种方法的可行性。

1　传统精对准误差模型建立

1.1捷联惯导系统误差模型

选取东北天坐标系为导航坐标系n系，右前上为机体坐标系b系，在不考虑垂直通道的加速度计偏置和速度误差时，建立静基座的误差模型如下［7］：

其中，δVE、δVN分别表示东、北方向的速度误差；表示东、北方向的等效加速度计常值漂移；φE、φN、 φU表示三个姿态失准角；εE、εN、 εU表示东、北、天向的等效陀螺常值漂移；ωie为地球自转角速度，g为当地重力加速度，L为当地纬度。

1.2状态方程建立

根据捷联系统误差模型，在粗对准获得载体的初始姿态矩阵后，可以使用卡尔曼滤波法进行精对准。首先建立系统的状态方程：

式中，

其中，I表示单位矩阵，W表示系统噪声矩阵。

1.3常规观测方程

在静基座条件下，传统的卡尔曼滤波常采用惯导解算的速度误差作为观测量。取东向和北向速度误差为观测量，设观测噪声为V，得到观测方程为：

由状态方程（式（2））和观测方程（式（3））组成常规对准系统方程：

将系统方程（式（4））离散化后，使用离散卡尔曼滤波算法对状态X进行估计，完成常规的精对准过程。

2　引入陀螺信息的快速对准方法

静基座下，常规对准方法采用速度误差为观测量，通过卡尔曼滤波方法完成精对准。该算法对φU估计时间长，这是由于其是利用水平用加速度计测量方位罗经效应引起的水平倾斜，然后通过积分得到速度误差进行估计的，陀螺信息没有直接参与初始对准。为了加快φU的估计速度，文献［2］、文献［3］将等效陀螺测量信息加入到观测方程中，加强对陀螺信息的利用。

2.1建立等效陀螺观测方程

在理想静基座条件下，假设导航坐标各轴系指向真东北天，陀螺仪测量没有误差，那么陀螺的输出应该为地球自转速度ωie在机体坐标系各轴上的投影，即然而实际情况中，由于惯性器件本身的误差和各种外界随机干扰，其输出必然带有误差，其中一部分是由于计算坐标系c系和导航坐标系n系的偏差角φ引起的，另一部分是由于陀螺仪自身的漂移引起的。

将式（6）展开，并把εb投影到n系中，得到方程组：

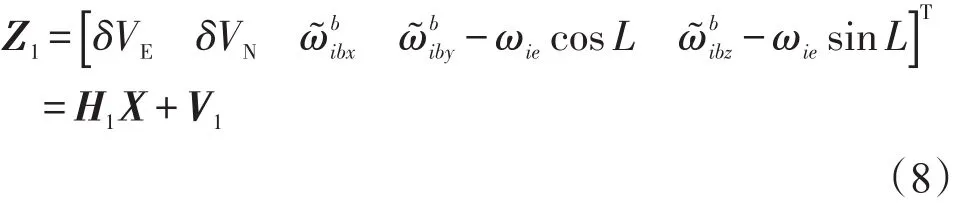
其中，

由式（2）和式（8）构成了快速对准系统方程：

2.2可观测性与可观测度分析

从系统可观测性和可观测度出发，比较常规对准系统（式（4））和快速对准系统（式（9））的对准效果。设式（4）和式（9）的可观测矩阵分别为Q和Q1，则有：

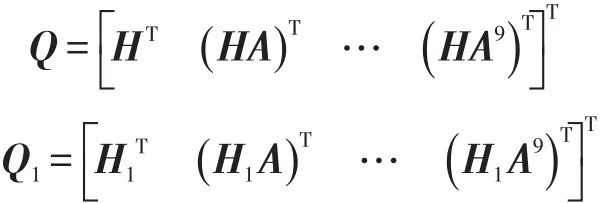
计算rank（Q）=rank（Q1）=7，说明两个系统均有三个不可观状态，一般认为是▽E、▽N和εE，这说明引入等效陀螺测量信息不能增加系统的可观测状态个数。由于初始对准的极限精度与这三个不可观测状态有关，故这两个系统的对准精度相当。

将Q和Q1进行奇异值分解Q=UΣVT，，得到：

可以看出，Σ与Σ1的区别就是εU对应的可观测度由常规方法的0.0006变成新方法的1，即可观测度显著提高，短时间内由近似不可观变为可观测。

3　快速双位置对准方案设计

传统单位置初始对准方法中，系统不完全可观，而且对准的极限精度与系统的不可观测状态有关。双位置对准法通过改变IMU位置，使系统变为完全可观测系统，估计出全部的状态变量，从而有效消除不可观测状态的影响，提高系统精度。文献［4］中指出，双位置对准采用航向角变化的效果最好，且当航向角转动180°时，所得到的第二位置具有最小航向角误差估计和最好的位置变化灵敏度。

3.1常规双位置对准方法

常规双位置对准方法采用系统方程完成精对准，并且两个位置使用一个卡尔曼滤波器。首先在第一位置进行对准，待方位失准角收敛后引入第二位置，继续进行对准，待方位失准角再次收敛后，IMU转回正常位置，对准结束。

该方法对准精度高，时间长。方位失准角φU和等效北向陀螺漂移εN估计速度慢，两者需要约300s才能稳定。为了使双位置对准达到最优精度，必须等到状态估计收敛后，才能引入第二位置，而且每一位置的对准时间均需300s，总共需要600s，大大制约了初始对准时间。同时由于对准过程中转位机构、惯性器件误差等因素影响，若滤波器参数设计不好会导致大的超调过程，致使对准时间变长。

3.2快速双位置对准流程

针对以上缺点，本文提出一种分段式滤波的双位置对准法，在两个位置分别采用两个卡尔曼滤波器进行状态估计，建立两个位置之间误差参数的数学关系，通过求解方程组获得各项误差参数，最后对系统进行一次修正，完成两位置精对准过程。同时在每个滤波器的观测方程中引入陀螺测量信息加快滤波器的收敛速度，达到快速对准的目的。

根据单位置对准的仿真结果分析，水平失准角的收敛速度很快，在十几秒内就可以达到稳定，而且精度很高，提升的空间不大。故在每段滤波完成后先进行水平精对准，然后进行方位失准角计算和修正。

根据分段滤波的思想，设计具体对准方案：

2）在位置1进行精对准，滤波器稳定后记录失准角φE、φN、φU和等效北向漂移εN的估计值，对进行水平修正但不修正方位角，然后进入导航状态。

3）按照转位要求，在一定时间内进行转位。为保证可观测度，转位角度要求在90°～270°之间。

4）在位置2重新进行精对准，记录第二次对准的估计值φE、φN、φU、εN。

通过两个位置记录数据进行误差参数计算，并对系统进行修正。

整个对准过程的基本流程如图1所示。

图1　双位置对准流程图Fig.1　Flow chart of two-position alignment

在本方案中，在当φU的估计精度达到要求后，才能对姿态更新矩阵作修正。修正前，φU以粗对准确定的姿态误差为初值进行传播，并未受到任何抑制，所以采用开环卡尔曼滤波，有利于误差信息的积累。

4　误差参数计算公式

4.1数据记录

快速双位置对准的本质是通过两个位置的精对准过程所获得的数据求解各个误差参数，包括姿态误差角、等效陀螺常值漂移等。

第一个位置精对准结束后，记录如下数据：

φE1、φN1、φU1——位置1东北天三个方向的失准角；

εN1——位置1等效北向陀螺漂移。第二个位置精对准结束后，记录如下数据：

φE2、φN2、φU2——位置2东北天三个方向的失准角；

εN2——位置2等效北向陀螺漂移。

4.2误差参数计算公式推导

在第一次精对准过程中，滤波器达到稳定后，位置1的状态估计值有以下关系：

其中，εE1为位置1的不可观测状态。

为了保证对准过程中方位失准角φU变化不大，在第一次精对准结束后进行水平修正。设粗对准完成后获得初始姿态矩阵为水平修正后的姿态矩阵为其中，

同理，位置2的状态估计值有以下关系：

接下来计算方位失准角φU，引入IMU坐标系b1、b2，在位置1时，坐标系b1的xyz轴分别与初始机体坐标系b右前上重合，在绕方位轴旋转θ角后到位置2的坐标系为b2，转换矩阵为：

分别计算两个位置的等效陀螺漂移：

为了保证计算精度，Cnb需经过误差修正：

根据仿真条件，采用分段卡尔曼滤波算法对本文中提出的双位置快速对准法进行10min的数学仿真。尽管在引入陀螺测量信息后只需要50s状态

当载体接近水平时，由于IMU按照方位轴进行旋转，天向通道误差参数对水平误差参数的计算基本没有影响，根据转换矩阵，可以得到误差参数有以下关系：

式中，εx、εy表示IMU上固连的陀螺仪常值漂移。

将式（10）和式（11）、式（12）、式（13）对应相减并整理，得到等效水平漂移的变化量为：

联立式（16）和式（17），得到：

其中，

解式（18）得水平陀螺仪误差参数：

在计算εx、εy后，可以根据式（16）计算两个位置的不可观测状态εE。

在获得εE后，根据式（12）计算φU，得：

最后对系统进行一次方位修正，整个对准过程结束。

5　仿真分析

5.1仿真条件

为了验证该算法的正确性，进行计算机仿真，设置仿真条件如下：

陀螺仪漂移：0.02（°）/h；

加速度计零偏：50μg；

粗对准后方位失准角：1°；

载体姿态角：均为0°；

转位速度：10（°）/s；

转位角度：180°。

5.2仿真结果与分析

首先在单位置条件下，进行常规对准系统和快速对准系统的对准效果比较仿真，结果如图2所示。可以看出，在引入陀螺测量信息后，方位失准角φU，等效北向漂移εN和等效天向漂移εU在50s内可以快速收敛，方位失准角的估计精度与常规算法相当。量可以快速收敛。但为了减小噪声和外界干扰，适当延长每一段精对准时间到100s，方位失准角估计结果如图3所示。

图2　单位置对准常规方法与快速算法对比图Fig.2　Comparison chart of conventional method and fast algorithm in one-position alignment

图3　双位置快速对准方位角误差估计曲线Fig.3　Estimated curve of azimuth error under fast twoposition Kalman filter

作为对比，当采用连续卡尔曼滤波，即两个位置用一个滤波器时，在第250s进行转位引入第二位置，方位角误差估计曲线如图4所示。

图4　连续卡尔曼滤波方位角误差估计曲线Fig.4　Estimated curve of azimuth error under continuous Kalman filter

通过新的双位置分段卡尔曼滤波对准方法得到的结果，利用式（12）、式（16）、式（19）和式（20）可计算得到陀螺仪等效漂移、方位失准角等参数，计算结果如表1所示。

综上可以得出以下结果：

表1　快速双位置对准估计结果Table 1　Result of fast two-position alignment

1）根据图2，当引入陀螺测量信息后，φU与εN的收敛速度比常规方法明显提升，εU也由近似不可观变为可观测。

2）比较图3和图4，受载体转位运动和惯导内部误差影响，采用一个滤波器的双位置对准算法在第二个位置的估计过程中超调较大且收敛缓慢，对准过程需要10min。采用双滤波器结构不存在这一问题，在每个位置很快收敛。而且在引入陀螺测量信息为观测量后，系统收敛速度明显提升，整个对准过程可以在4min内完成。

3）根据表1的计算结果，采用双位置快速对准法，可以准确地估计出方位失准角和陀螺仪漂移。而且经过计算修正以后，方位对准的精度达到30''，实现快速、准确的对准。

6　结论

本文针对传统双位置对准中方位失准角收敛速度慢的问题，提出了引入陀螺测量信息的快速双位置对准算法。该方法充分利用了陀螺输出信息，改善了系统的可观测性和可观测度，并且采用双位置双滤波器的结构，避免了旋转过程中由于系统超调而引起的收敛速度过慢。对准结束后，根据记录数据与数据之间的物理关系用求解方程组的方法求解各项误差参数。通过计算机仿真验证，对准过程可在4min内完成，采用常值漂移为0.02（°）/h的陀螺，方位姿态角估计误差在1'之内。该方法切实可行，有一定的应用参考价值。

［1］曹通.光纤陀螺捷联惯导系统在线对准及标定技术研究［D］.哈尔滨工程大学，2012. CAO Tong.On-line alignment and calibration techniqueof fiber optic gyroscope SINS［D］.Harbin Engineering University，2012.

［2］高伟熙，缪玲娟，倪茂林.一种引入陀螺角速度信息的快速对准方法［J］.宇航学报，2010，31（6）∶1597-1601. GAO Wei-xi，MIAO Ling-juan，NI Mao-lin.A fast alignment method based on gyro palstance information［J］. Journal ofAstronautics，2010，31（6）∶1597-1601.

［3］黄湘远，汤霞清，郭理彬.基于等效陀螺的捷联惯导快速两位置对准仿真［J］.计算机仿真，2012，29（3）∶68-71. HUANG Xiang-yuan，TANG Xia-qing，GUO Li-bin. Simulation of fast two-position alignment of SINS based on equivalent gyro［J］.Computer Simulation，2012，29 （3）∶68-71.

［4］钱伟行，刘建业，赵伟，赵文芳.基于转动基座的SINS初始对准方法研究［J］.宇航学报，2008，29（3）∶928-932. QIAN Wei-xing，LIU Jian-ye，ZHAO Wei，ZHAO Wenfang.Study of SINS initial alignment based on rotating susceptor［J］.Journal of Astronautics，2008，29（3）∶928-932.

［5］周绍磊，吴修振，徐海刚，等.一种新的捷联惯导快速双位置对准方法［J］.中国惯性技术学报，2012，20（5）∶525-529. ZHOU Shao-lei，WU Xiu-zhen，XU Hai-gang，et al.New rapid two-position alignment method of SINS［J］.Journal of Chinese Inertial Technology，2012，20（5）∶525-529.

［6］高伟熙，缪玲娟，沈军.一种分段快速捷联惯导静基座自对准新方法［C］.第29届中国控制会议，2010（7）∶3307-3310. GAO Wei-xi，MIAO Ling-juan，SHEN Jun.A nes piecewise fast alignment methoh for SINS stationary selfalignment［C］.Proceedings of the 29thChinese Control Conference，2010（7）∶3307-3310.

［7］秦永元.惯性导航［M］.北京∶科学出版社，2006. QIN Yong-yuan.Inertial navigation［M］.Beijing∶Science Press，2006.

［8］ Zhang Ludong，Liang Junxiang，Wu Meiping，et al.Research on auto compensation technique of strapdown inertial navigation systems［C］.2009 International Asia Conference on Informatics in Control，Automation and Robotics，2009∶350-359.

［9］刘志琴，王新龙.捷联惯导系统最优多位置对准的确定与分析［J］.北京航空航天大学学报，2013，39（3）∶330-334. LIU Zhi-qin，WANG Xin-long.Confirmation and analysis on the optimal multipostion alignment of strapdown inertial navigation system［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39（3）∶330-334.

［10］Li An，Chang Guobin，Qin Fangjun，et al.Improved precision of strapdown inertial navigation system brought by dual-axis continuous rotation of inertial measurement unit［C］.2010 2ndInternational Asia Conference on Informatics in Control，Automation and Robotics，2010∶284-287.

［11］Gebre-Egziabher D，Elkaim G H.MAV attitude determination by vector matching［J］.IEEE Transactions on Aerosapce and Electronic Systems，2008，44（3）∶1011-1028.

［12］ Garry A，John T，David C.Riccati equation and EM alogrithm convergence for inertial navigation alignment ［J］.IEEE Transactions on Signal Processing，2009，57 （1）∶370-375.

Fast Two-positionAlignment of SINS Based on Gyro Observation Information

LI Yi，YANG Meng-xing，XU Bing-hua
（The 16thInstitute，ChinaAerospace Science and Technology Corporation，Xi’an 710100）

To solve the contradiction between rapid response and high precision of SINS，a rapid two-position alignment scheme with gyro error observation information on the static base is presented.By analyzing conventional alignment method，the observation with gyro error information was increased to improve the system observability and the convergence speed of Kalman filter.To solve the problem of slow estimation of Tazimuth misalignment angle in traditional two-position alignment，the alignment method of two-position and two-filter is presented.The simulation results show that，the horizontal and azimuth errors are approximately equal.These show that the method is feasible and very consultation to improve the system observability and reduce the alignment time greatly.

SINS；Kalman filter；two-position alignment；observability

U666.1

A

1674-5558（2016）01-01065

10.3969/j.issn.1674-5558.2016.02.006

2015-01-19

李逸，男，精密仪器与机械专业，硕士，研究方向为高精度捷联惯性导航研究。