双丝杠驱动进给单元轴向刚度模型及影响因素分析

许向荣，鹿群鹏，宋现春，姜洪奎

(山东建筑大学 机电工程学院,山东 济南 250101)



双丝杠驱动进给单元轴向刚度模型及影响因素分析

许向荣，鹿群鹏，宋现春，姜洪奎

(山东建筑大学 机电工程学院,山东 济南 250101)

双丝杠驱动进给单元在高性能数控机床中的应用较为广泛，研究其动态特性对于提高数控机床的加工性能具有重要的意义。文章基于关键滚动功能部件结合面刚度各个方向耦合的影响，围绕双丝杠驱动进给单元轴向刚度进行了研究分析，通过研究双丝杠驱动进给单元的轴向刚度模型，结合动力学和Hertz接触理论的相关知识，推导其各组成部分的刚度计算公式，探索其主要影响因素及关系曲线。结果表明：双丝杠驱动进给单元的轴向刚度主要受到滚珠丝杠副、支承轴承的结构参数，螺母位置以及两根丝杠跨距的影响；支承轴承结构参数的变化，会引起进给单元轴向刚度的明显变化；螺母位置是进给单元轴向刚度的主要影响因素，在两端固定的方式下其轴向刚度中间最小，在机床加工过程中，应尽量避免在丝杠的中间位置进行操作。

结合面；双丝杠驱动； 进给单元； 轴向刚度

0　引言

与传统的单丝杠驱动进给系统相比，双丝杠驱动进给系统有很大的优势，如高精度、高刚度、低振动等，因此，双丝杠驱动进给系统日益成为高性能数控机床、加工中心研究领域的一个热点[1-3]。

目前，国内外学者纷纷围绕双丝杠驱动进给系统展开了理论和实验方面的研究。Hiramoto等介绍了重心驱动原理，设计了工作台和主轴均采用重心驱动的机床模型和实际的双驱动进给系统的实验模型，通过实验发现重心驱动进给系统可以明显地减小机床的振动[1]，但是缺乏理论支持。Gomand等采用理论建模的方法，建立了龙门数控机床双驱动进给系统的数学模型，推导了丝杠轴向振动方程，并分析了丝杠变形对其静动态特性的影响[2]。

而国内这方面的研究起点较晚，但随着高性能数控机床的快速发展，各科研院所也加快了对双驱动进给系统的研究。何王勇等仅考虑双滚珠丝杠同步驱动轴的同步轴间负载耦合关系及丝杠、螺母的轴向扭转耦合关系的影响，建立了其动力学模型，推导了动力学方程，并对其固有频率进行了理论计算[3]。唐余林和芮执元等以铣车复合加工中心双驱进给系统为研究对象，将双丝杠耦合转化到横梁的各个方向上的运动，建立了双驱进给系统动力学模型及其动力学方程，并进行了模态分析与谐响应分析，找到了系统的薄弱环节，并对其进行了优化[4-5]。郭崇高等采用有限元分析和虚拟样机技术，建立了双驱动进给系统动力学模型，采用拉格朗日方程，推导了系统运动微分方程，获得了其主要模态参数，最后对其进行了模态分析和谐响应分析，得出两对导轨滑块与两根丝杠跨距等对系统动态性能的影响，并提出了相应的改进措施[6]。丁喜合等建立了二自由度系统振动模型，采用单因素分析方法研究了丝杠跨距和导轨跨距对双丝杠驱动进给系统动态特性的影响[7-9]。但是对于导轨跨距的影响研究中没有考虑导轨法向结合面的刚度。白茹通过拉格朗日方程在广义坐标下的变换建立了双驱滚珠丝杠进给系统的实体模型，并设计了加工中心双驱进给系统动态性能实验平台，对双驱滚珠丝杠进给系统的动态特性进行了分析，提出了双驱进给系统的改善措施,为进一步研究奠定了理论基础[10]。夏田等建立了双丝杠驱动工作台动力学模型，找到了位置响应的主要因素，对重心驱动工作台结构进行了改进，并建立了有限元分析模型，进行了模态分析和谐响应分析。其研究发现进给轴刚度是影响位置精度的关键因素，恰当选择导轨的间距对提高工作台的动态响应性能有重要的作用[11]。杨勇等采用理论建模的方法，对MCH63卧式加工中心“重心驱动”机构建立了动力学模型，通过实验获得了导轨结合面的刚度和阻尼值，并计算分析了导轨结合面刚度、阻尼值及“重心驱动”结构对机床动力学性能的影响[12]。

上述对于双丝杠驱动进给系统的研究,多数采用建立动力学模型，推导动力学方程，有限元模态分析和谐响应分析的思路对进给系统动态特性进行研究，没有专门针对系统刚度进行的研究。因此，文章考虑结合面刚度各个方向耦合的影响，建立了双丝杠驱动进给单元的动力学模型，并在此基础上建立了其轴向刚度模型，分析研究了影响进给单元刚度的主要因素，获得了其相应的关系曲线，为后面分析双丝杠驱动进给单元的动态特性奠定了基础。

1　双丝杠驱动进给单元组成

双丝杠驱动进给单元结构组成示意图，如图1(a)所示，主要包括：两台相同型号的伺服电机，两套相同型号的滚珠丝杠副，两套相同型号的支承轴承，两套相同型号的直线滚动导轨副以及拖板组成。由两台伺服电机同步驱动两套滚珠丝杠副带动拖板沿着直线滚动导轨副做往复直线运动，实现进给驱动。

2　单元轴向刚度模型

由于60%的机床振动产生于其结合部[13-14]，因此在研究双丝杠驱动进给单元的动态特性时，不能忽略结合面的影响，尤其是其主要滚动功能部件，如滚珠丝杠副、滚动轴承、直线滚动导轨副结合部的影响。这三种部件作为双丝杠驱动进给单元的关键部件，其变形及刚度对整个系统的变形及刚度特性都有很重要的影响。因此，在该部分里，文章依据动力学相关理论，建立了双丝杠驱动进给单元动力学模型，如图1(b)所示。并在此基础上建立了进给单元的轴向刚度模型。然后，基于Hertz接触理论[15]，推导了滚珠丝杠副、支承轴承结合面的接触变形和接触刚度的计算公式，进而获得进给单元的轴向刚度计算公式；最后，通过实例计算分析研究了其各个设计参数对进给单元轴向刚度的影响。

依据图1(b),可以建立双丝杠驱动进给单元的轴向刚度模型，如图1(c)所示。

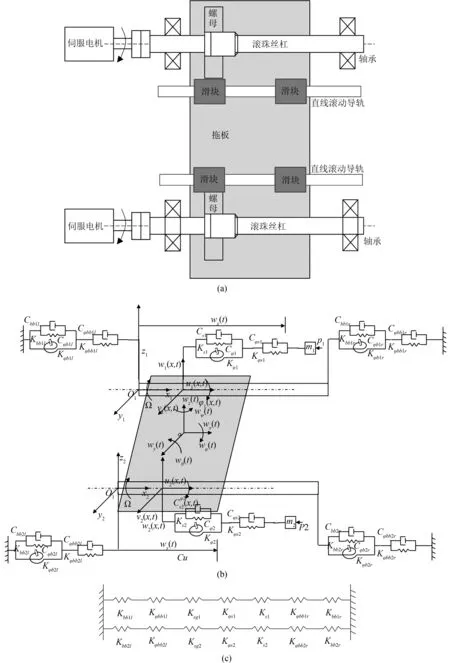
图1　双丝杠驱动进给单元图(a) 结构示意图；(b)动力学模型；(c) 轴向刚度模型

从图1(c)可以看出，由弹簧串、并联的刚度系数计算方法可得出双丝杠驱动进给单元的轴向刚度由式(1)、(2)表示为

(1)

式中：Kfi(i=1、2)为第i根滚珠丝杠传动系统的轴向刚度，N/mm，可以根据式(2)进行计算，Ksi(i=1、2)是滚珠丝杠副结合面的轴向刚度，N/mm；kφsi(i=1、2)是滚珠丝杠扭转—轴向耦合刚度，N/mm；Kbbil(i=1、2)、Kbbir(i=1、2)分别是左、右端支承轴承结合面的轴向刚度，N/mm；Kφbbil(i=1、2)、Kbbir(i=1、2)分别是左端轴承扭转—轴向耦合刚度，N/mm；Ksgi(i=1、2)是由拖板耦合引起的滚珠丝杠轴向刚度，N/mm。

2.1滚珠丝杠副结合面的轴向刚度计算

相关研究表明，两个曲面物体互相接触、挤压，其在接触部位的应力分布与接触面的形状、尺寸及表面粗糙度等许多因素有关[14]。1881年，Hertz指出两光滑弹性体在相互作用的力下发生的接触变形及应力分布应满足Hertz接触假设[15]：

(1) 接触物体只产生弹性变形，服从胡克定律。

(2) 接触表面充分光滑，不考虑接触面的介质以及动摩擦力的影响。

(3) 接触面的尺寸与接触物体表面的曲率半径相比是小量。

满足上述假设的接触为赫兹接触。

在上述假设下，忽略工作载荷分布不均匀的影响，单螺母丝杠副在法向载荷Q作用下，螺母滚道面

与丝杠滚道面间由于法向弹性接触变形所产生的弹性变形量[16-18]δn由式(3)表示为

(3)

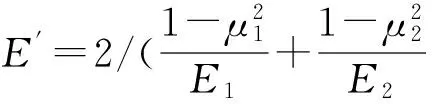
根据几何关系，可以得到丝杠相对于螺母的轴向弹性位移δa由式(4)表示为

δa=δncosλ/sinβ

(4)

将式(3)带入式(4)，可得单螺母滚珠丝杠副的载荷变形关系由式(5)表示为

(5)

式中：Fa为螺母受到的轴向推力，N，Fa=zQsinβcosλ；β、λ分别为滚珠丝杠副的接触角和螺旋升角，°；z为滚珠丝杠副的滚珠数目。

将式(5)两边分别对δa求导，可得单螺母丝杠副的轴向接触刚度式(6)为

(6)

通常采用双螺母预紧的方法减小或消除滚珠丝杠副的轴向间隙，以提高其轴向接触刚度。因此，在上述单螺母滚珠丝杠副研究上，可以得到双螺母滚珠丝杠副结合面的轴向接触刚度Ksi(i=1,2)[13]由式(7)表示为

(7)

式中：PP为丝杠上承受的预紧法向力，N；F为轴向载荷，N。

由式(7)可以看出，在轴向载荷作用下，双螺母滚珠丝杠副结合面的轴向接触刚度与轴向载荷、预紧力、螺旋升角、接触角等几何参数有关。

2.2拖板引起的滚珠丝杠轴向刚度计算

工作过程中，除了轴向载荷会引起单根丝杠轴向变形外，拖板会使得两根丝杠产生耦合变形，进而影响到进给单元的轴向动态变形量。在轴向载荷作用下，丝杠会发生拉压变形，其大小与两端的支承方式及螺母的工作位置有关。设支承方式为两端固定方式，由于两根滚珠丝杠通过拖板连接在一起，假设两根丝杠不能实现同步运动，则势必会出现如图2所示的耦合作用。

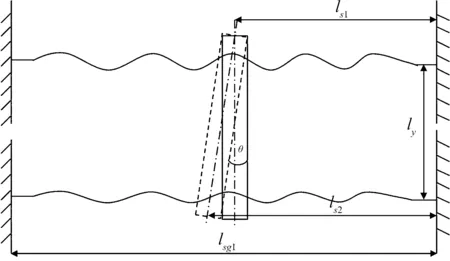
图2　两端固定安装方式示意图

图2中，lsi(i=1,2)为丝杠i支承与螺母间的距离，mm；lsgi(i=1,2)为丝杠i的长度，mm；ly为两根滚珠丝杠跨距，mm。

由图2可以看出几何关系式(8)为

ls2=lyθ+ls1

(8)

因此，对于单根滚珠丝杠来说，其轴向变形量式(9)、(10)为

(9)

(10)

式中：δs1、δs2分别为丝杠1、2的轴向直线位移量，mm；F为丝杠的轴向载荷，N；d1为丝杠的螺纹内径，mm；θ为两根丝杠不同步时，拖板的扭转角度；lsi(i=1,2)为丝杠i支承与螺母间的距离，mm；lsgi(i=1,2)为丝杠i的长度，mm；ly为两根滚珠丝杠跨距，mm；E为材料的纵向弹性模量，钢的E=207 GPa。

因此，由拖板引起的滚珠丝杠轴向刚度由式(11)、(12)表示为

(11)

(12)

从式(11)，(12)中可以看出，影响进给单元中拖板引起的滚珠丝杠轴向刚度的主要因素有：两根丝杠的跨距ly，螺母的位置ls1以及两根丝杠不同步时拖板的扭转角度θ。

2.3滚珠丝杠的扭转—轴向耦合刚度计算

在驱动力矩和轴向载荷作用下，滚珠丝杠时会产生扭转变形，从而引起螺母轴向位移，因而会影响丝杠轴向动态变形量。根据材料力学相关知识，可得两端固定时单根滚珠丝杠在扭矩作用下产生的轴向变形量由式(13)表示为

(13)

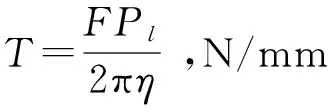
因此，丝杠的扭转—轴向耦合刚度式由(14)表示为

(14)

2.4支承轴承结合面的轴向刚度计算

鉴于滚动轴承与滚珠丝杠副结构和受力的相似性，之前求滚珠丝杠副轴向接触刚度计算时的假设条件，仍适用于支承系统轴向刚度的计算，且单滚珠丝杠副轴向接触刚度计算分析方法也同样适用于支承系统轴向刚度的计算。因此，忽略工作载荷分布不均匀的影响，设螺旋升角，则支承轴承结合面的轴向刚度式(15)为

(15)

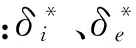
由于丝杠工作时对滚动轴承的轴向和径向作用力比较小，可以忽略不计，所以此处认为轴向力Fa为滚动轴承的预紧力。

从式(15)可以看出，影响支承轴承结合面轴向刚度的主要因素有：滚珠个数，接触角及密合度。根据丝杠两端轴承的布置方式以及弹性体串并联时的刚度计算公式即可对进给单元支承轴承的轴向刚度Kbbi进行计算。

2.5支承轴承的扭转—轴向耦合刚度计算

相对于滚珠丝杠的扭转变形，支承轴承的扭转变形Kφbbi可以忽略不计，因此其对轴向刚度的影响也可以忽略不计。

Kφbbi=0

(16)

3　单元轴向刚度影响因素分析

从第2部分分别得到了双丝杠驱动进给单元刚度模型中各部分的刚度计算公式，因此只要已知滚珠丝杠副和支承轴承的结构参数，就可以得到整个进给单元的轴向刚度。下面通过具体实例计算，采用单因素分析方法对进给单元的轴向刚度影响因素进行分析，其中滚珠丝杠副和支承轴承的具体参数见表1和2。

表1　G3210—4滚珠丝杠副结构参数

表2　角接触球轴承结构参数

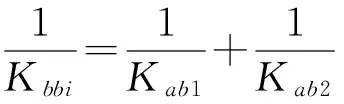
从图3中可以看出，双丝杠驱动进给单元轴向刚度主要受到滚珠丝杠副、支承轴承的结构参数，螺母位置以及两根丝杠跨距的影响为

(1) 双丝杠驱动进给单元的轴向刚度随着滚珠丝杠副的接触角、预紧力、滚珠数目以及螺旋升角的增大而增大，而呈非线性变化。其轴向刚度随着曲率比的增加而明显降低。轴向载荷的增加使其轴向刚度呈线性增大。

(2) 增大支承轴承的接触角，滚珠数目都可以使其轴向刚度有明显的提高，而且呈非线性变化。其轴向刚度随着曲率比的增加而线性降低。

(3) 螺母位置对于双丝杠驱动进给单元轴向刚度有显著的影响，还跟支承方式有直接的关系，此处选择两端固定的方式，因此，其轴向刚度两端最大，而中间最小；两根丝杠跨距的增加使其轴向刚度呈线性增大；拖板扭转角使得轴向刚度非线性增大。

但是，可以发现双丝杠驱动进给单元的轴向刚度受支承轴承结构参数，尤其是受轴承接触角的影响比较大，变化范围比较显著。

因此,在设计时需要寻找最优滚珠丝杠副和支承轴承的结构参数，合理布置螺母位置、选择丝杠的跨距，有利于提高双丝杠驱动进给单元的轴向刚度。

为了找到影响双丝杠驱动进给单元轴向刚度的主要因素，对以上各部分进行了比例计算，计算结果如图4所示，其中，拖板引起的丝杠耦合刚度所占比例最大。因此，影响拖板引起的丝杠耦合刚度的主要因素，便是影响进给单元轴向刚度的主要因素。由式(9)、(10)和图3可以看出螺母位置是影响进给单元轴向刚度的主要因素。螺母处于丝杠中间位置时进给单元的刚度最小，因此，在机床加工过程中，尽量避免在此位置进行加工操作。

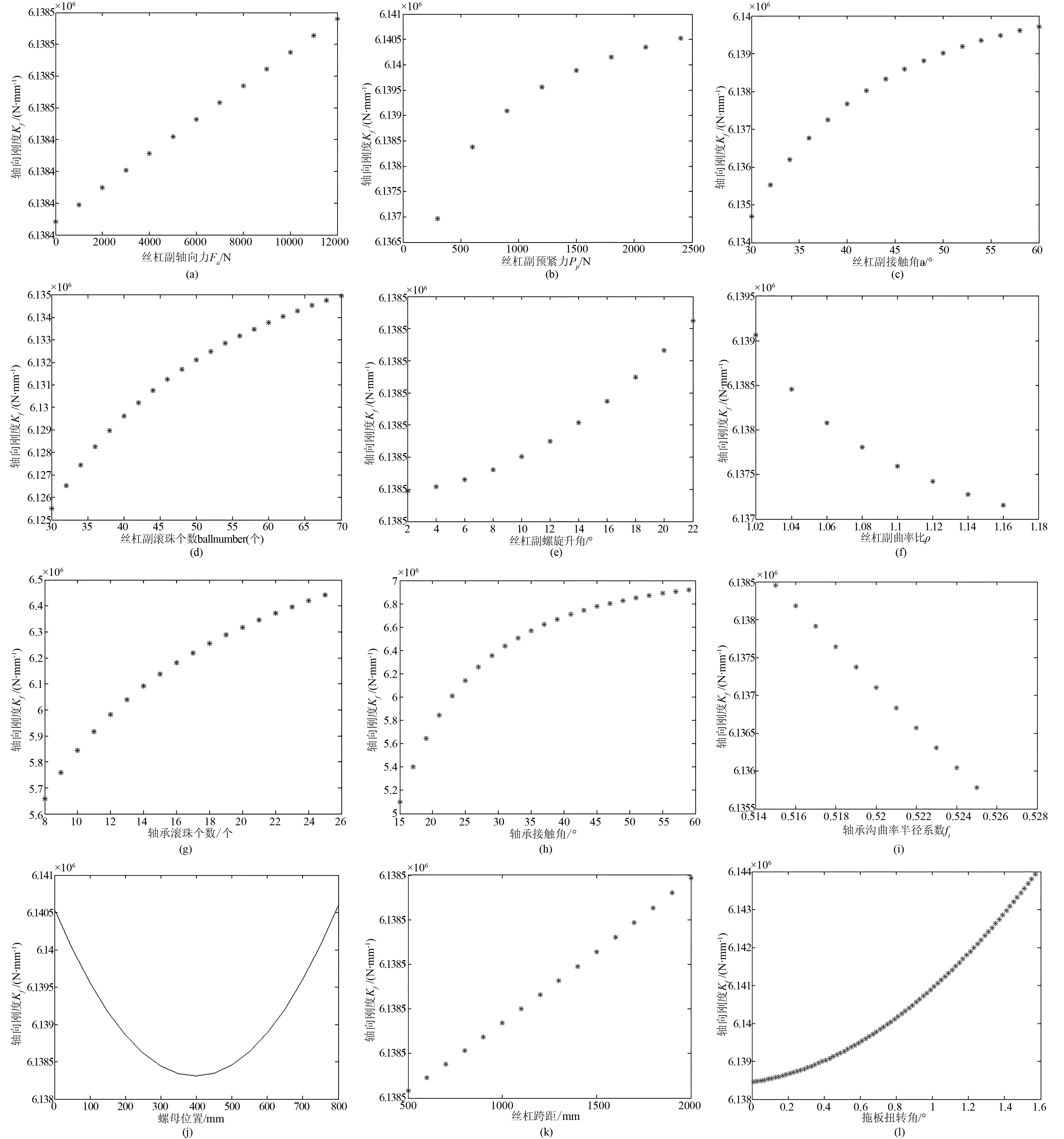
图3　进给单元影响因素分析关系曲线图(a) 丝杠轴向载荷的影响 ；(b) 丝杠预紧力的影响；(c) 丝杠接触角的影响 ；(d) 丝杠滚珠个数的影响(e) 丝杠螺旋升角的影响；(f) 丝杠曲率比的影响；(g) 轴承滚珠个数的影响 ；(h) 轴承接触角的影响(i) 轴承沟曲率半径系数的影响；(j) 螺母位置的影响；(k) 两根丝杠跨距的影响;(l) 拖板扭转角的影响

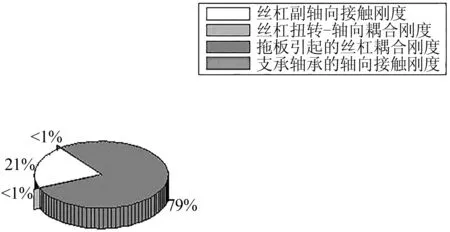
图4　进给单元轴向刚度比例计算图

4　结论

通过上述研究可知：

(1) 双丝杠驱动进给单元的轴向刚度主要受到滚珠丝杠副、支承轴承的结构参数，螺母位置以及两根丝杠跨距的影响；

(2) 支承轴承结构参数，尤其是其接触角的变化，会引起进给单元轴向刚度的明显变化；

(3) 拖板引起的丝杠耦合刚度所占比例最大，其影响因素——螺母位置是影响进给单元的主要因素。

(4) 当采用两端固定支承方式时，螺母处于丝杠中间位置时进给单元的刚度最小，要尽量避免机床在丝杠中间位置处进行加工操作。

[1]Hiramoto K., Hansel A., Ding S.,etal. A study on the drive at center of gravity(DCG) feed principle and its application for development of high performance machine tool systems[J]. CIRP Annals-Manufacturing Technology, 2005, 54(1): 333-336.

[2]Gomand J., Kestelyn X.. Dual-drive gantry stage decoupling dynamic analysis based on a coupling model[J]. Electromotion,2008,15( 2): 94-98 .

[3]何王勇,唐小琦,李勇波. 基于有限元的双滚珠丝杠同步驱动轴动力学建模与分析[J]. 制造技术与机床,2010(12):83-86.

[4]唐余林. 铣车复合加工中心双驱进给系统动力学分析与仿真[D]. 兰州：兰州理工大学,2014.

[5]芮执元,张国涛,冯瑞成,等. 双驱进给系统的刚柔耦合模型及参数优化[J]. 兰州理工大学学报,2015(4):41-45.

[6]郭崇嵩,芮执元,刘军. 铣车加工中心双驱进给系统静动态特性分析[J]. 组合机床与自动化加工技术,2012(6):5-8.

[7]丁喜合,袁军堂,汪振华, 等. 双丝杠驱动直线进给系统动态特性分析[J]. 组合机床与自动化加工技术,2014(3):26-28.

[8]丁喜合. 滚动支撑双驱动直线进给系统动态特性分析和试验[D]. 南京：南京理工大学,2014.

[9]丁喜合,袁军堂,汪振华, 等. 数控机床双丝杠驱动直线进给系统静动态特性分析[J]. 机械设计与制造,2014(3):155-157.

[10]白茹. 加工中心双驱进给系统动态特性研究[D]. 兰州：兰州理工大学,2014.

[11]夏田,王志军,缑建文, 等. 基于重心驱动进给系统工作台动态性能分析[J]. 组合机床与自动化加工技术,2014(9):109-112.

[12]杨勇,叶文华,刘世豪, 等. 结合面参数以及“重心驱动”对机床动力学性能的影响[J]. 组合机床与自动化加工技术,2010(7):17-21.

[13]廖伯瑜, 周新民, 尹志宏. 现代机械动力学及其工程应用[M]. 北京: 机械工业出版社, 2004.

[14]程光仁, 施祖康, 张超鹏. 滚珠螺旋传动设计基础[M].北京: 机械工业出版社, 1987.

[15]Hertz H. On the contact of elastic solids [J]. Journal Fur Die Reine Und Angewandte Mathematic, 1882, 92 :156-171.

[16]许向荣. 滚珠丝杠副直线导轨进给单元动态性能研究[D]. 济南:山东大学,2011.

[17]姜洪奎. 大导程滚珠丝杠副动力学性能与加工方法研究[D].济南:山东大学,2007.

[18]何纪承. 高速滚珠丝杠副动力学性能分析及试验研究[D]. 济南:山东建筑大学,2012.

(学科责编：吴芹)

The model and influencing factors analysis of axial stiffness of dual ball screw driving feed unit

Xu Xiangrong，Lu Qunpeng, Song Xianchun,etal.

(School of Mechanical and Electronic Engineering, Shandong Jiangzhu University, Jinan 250101,China)

Abstract： Dual ball screw driving feed unit has been used increasingly in the high performance CNC machine tool, so it is very significant to study the dynamic characteristics of dual ball screw driving feed unit for improving the processing performance of NC machine tool. Considering the coupled influence of the stiffness of key rolling joint surface, the research on axial stiffness of dual ball screw driving feed unit is carried on. An axial stiffness model of dual ball screw driving feed unit is built, stiffness calculation equations of each component are deduced based on dynamics and Hertz contact theory and its main influencing factors and their relationship curves are obtained. The results show that the axial stiffness of dual ball screw driving feed unit changes slightly with the structural parameters of ball screw pair, but changes obviously with the structural parameters of ball bearing. Ball screw span makes the axial stiffness linearly increase. Torsion angle makes the axial stiffness nonlinearly increase. The influence of nut position is related to its support mode. Through calculation of stiffness proportion, nut position is the main influence factor on the axial stiffness: under both ends fixed, the axial stiffness is the largest at both ends and smallest at mid position. As a result, during machining process of CNC, operation at middle position need to be avoided.

joint surface; dual ball screw driving; feed unit; axial stiffness

2015-12-17

国家自然科学基金项目(51205235)；山东建筑大学校内博士基金项目(XNBS1246)

许向荣(1978-)，女，副教授，博士，主要从事机电系统精密测控及系统动力学等方面的研究.E-mail：xt7875@163.com

1673-7644(2016)02-0125-08

TH132.1

A